Poliedro uniforme

Poliedro isogonal con caras regulares

Algunos ejemplos de poliedros uniformes: prisma triangular , antiprisma cuadrado , tetraedro regular en el sólido platónico , cuboctaedro en el sólido arquimediano , pequeño dodecaedro estrellado en el poliedro de Kepler-Poinsot y dodecadodecaedro romo en el poliedro estrellado uniforme .

En geometría , un poliedro uniforme tiene polígonos regulares como caras y es transitivo por vértices (existe una isometría que proyecta cualquier vértice sobre cualquier otro). De ello se deduce que todos los vértices son congruentes . Los poliedros uniformes pueden ser regulares (si también son transitivos por caras y aristas ), cuasiregulares (si también son transitivos por aristas pero no por caras) o semirregulares (si no son transitivos por aristas ni por caras). Las caras y los vértices no necesitan ser convexos , por lo que muchos de los poliedros uniformes también son poliedros estrella .

Existen dos clases infinitas de poliedros uniformes, junto con otros 75 poliedros. Son 2 clases infinitas de prismas y antiprismas , los poliedros convexos como en 5 sólidos platónicos y 13 sólidos arquimedianos —2 cuasirregulares y 11 semirregulares— los poliedros estrella no convexos como en 4 poliedros de Kepler-Poinsot y 53 poliedros estrella uniformes —14 cuasirregulares y 39 semirregulares—. También hay muchos poliedros uniformes degenerados con pares de aristas que coinciden, incluyendo uno encontrado por John Skilling llamado el gran dirhombidodecaedro desprovisto , la figura de Skilling. ^[1]

Los poliedros duales y uniformes son de cara transitiva (isoédricos) y tienen figuras de vértice regulares , y generalmente se clasifican en paralelo con su poliedro dual (uniforme). El dual de un poliedro regular es regular, mientras que el dual de un sólido arquimediano es un sólido catalán .

El concepto de poliedro uniforme es un caso especial del concepto de politopo uniforme , que también se aplica a formas en el espacio de mayor dimensión (o menor dimensión).

Definición

El pecado original en la teoría de los poliedros se remonta a Euclides, y a través de Kepler, Poinsot, Cauchy y muchos otros sigue afectando a todos los trabajos sobre este tema (incluido el del autor). Surge del hecho de que el uso tradicional del término "poliedros regulares" era, y es, contrario a la sintaxis y a la lógica: las palabras parecen implicar que estamos tratando, entre los objetos que llamamos "poliedros", con aquellos especiales que merecen ser llamados "regulares". Pero en cada etapa -Euclides, Kepler, Poinsot, Hess, Brückner, ...- los escritores no lograron definir cuáles son los "poliedros" entre los cuales están encontrando los "regulares".

(Branko Grünbaum 1994)

Coxeter, Longuet-Higgins y Miller (1954) definen los poliedros uniformes como poliedros transitivos de vértice con caras regulares. Definen un poliedro como un conjunto finito de polígonos de modo que cada lado de un polígono es un lado de solo otro polígono, de modo que ningún subconjunto propio no vacío de los polígonos tiene la misma propiedad. Por polígono se refieren implícitamente a un polígono en el espacio euclidiano tridimensional; se permite que estos no sean convexos y se intersequen entre sí. ^[2]

Existen algunas generalizaciones del concepto de poliedro uniforme. Si se descarta el supuesto de conectividad, se obtienen compuestos uniformes, que pueden dividirse como una unión de poliedros, como el compuesto de 5 cubos. Si descartamos la condición de que la realización del poliedro no sea degenerada, se obtienen los llamados poliedros uniformes degenerados. Estos requieren una definición más general de poliedro. Grünbaum (1994) dio una definición bastante complicada de poliedro, mientras que McMullen y Schulte (2002) dieron una definición más simple y general de poliedro: en su terminología, un poliedro es un politopo abstracto bidimensional con una realización tridimensional no degenerada. Aquí, un politopo abstracto es un conjunto de sus "caras" que satisfacen varias condiciones, una realización es una función desde sus vértices hasta algún espacio y la realización se denomina no degenerada si dos caras distintas del politopo abstracto tienen realizaciones distintas. Algunas de las formas en que pueden degenerarse son las siguientes:

Caras ocultas. Algunos poliedros tienen caras ocultas, en el sentido de que no se puede ver ningún punto de su interior desde el exterior. Estos no suelen considerarse poliedros uniformes.
Compuestos degenerados. Algunos poliedros tienen múltiples aristas y sus caras son las caras de dos o más poliedros, aunque no son compuestos en el sentido anterior, ya que los poliedros comparten aristas.
Coberturas dobles. Algunos poliedros no orientables tienen coberturas dobles que satisfacen la definición de poliedro uniforme. Estas coberturas dobles tienen caras, aristas y vértices duplicados. Por lo general, no se cuentan como poliedros uniformes.
Caras dobles. Existen varios poliedros con caras dobles producidos mediante la construcción de Wythoff. La mayoría de los autores no permiten caras dobles y las eliminan como parte de la construcción.
Aristas dobles. La figura de Skilling tiene la propiedad de tener aristas dobles (como en los poliedros uniformes degenerados), pero sus caras no pueden escribirse como una unión de dos poliedros uniformes.

Historia

Poliedros regulares convexos

Los sólidos platónicos se remontan a los griegos clásicos y fueron estudiados por los pitagóricos , Platón (c. 424 – 348 a. C.), Teeteto (c. 417 a. C. – 369 a. C.), Timeo de Locri (c. 420–380 a. C.) y Euclides (hacia el 300 a. C.). Los etruscos descubrieron el dodecaedro regular antes del 500 a. C. ^[3]

Poliedros convexos uniformes no regulares

El cuboctaedro era conocido por Platón .
Arquímedes (287 a. C. – 212 a. C.) descubrió los 13 sólidos arquimedianos . Su libro original sobre el tema se perdió, pero Pappus de Alejandría (c. 290 – c. 350 d. C.) mencionó que Arquímedes enumeró 13 poliedros.
Piero della Francesca (1415 – 1492) redescubrió las cinco truncaciones de los sólidos platónicos (tetraedro truncado, octaedro truncado, cubo truncado, dodecaedro truncado e icosaedro truncado) e incluyó ilustraciones y cálculos de sus propiedades métricas en su libro De quinque corporibus regularibus . También analizó el cuboctaedro en otro libro. ^[4]
Luca Pacioli plagió la obra de Francesca en De divina proporcionale en 1509, añadiendo el rombicuboctaedro , llamándolo icosihexaedro por sus 26 caras, que fue dibujado por Leonardo da Vinci .
Johannes Kepler (1571-1630) fue el primero en publicar la lista completa de sólidos arquimedianos , en 1619. También identificó las infinitas familias de prismas y antiprismas uniformes .

Poliedros estrellados regulares

Kepler (1619) descubrió dos de los poliedros regulares de Kepler-Poinsot , el pequeño dodecaedro estrellado y el gran dodecaedro estrellado .
Louis Poinsot (1809) descubrió los otros dos, el gran dodecaedro y el gran icosaedro .
El juego de cuatro fue demostrado completo por Augustin-Louis Cauchy en 1813 y bautizado con el nombre de Arthur Cayley en 1859.

Otros 53 poliedros estelares no regulares

De los 53 restantes, Edmund Hess (1878) descubrió 2, Albert Badoureau (1881) descubrió 36 más y Pitsch (1881) descubrió de forma independiente 18, de los cuales 3 no habían sido descubiertos previamente. En conjunto, estos dieron lugar a 41 poliedros.
El geómetra HSM Coxeter descubrió los doce restantes en colaboración con JCP Miller (1930-1932), pero no los publicó. MS Longuet-Higgins y HC Longuet-Higgins descubrieron once de ellos de forma independiente. Lesavre y Mercier redescubrieron cinco de ellos en 1947.
Coxeter, Longuet-Higgins y Miller (1954) publicaron la lista de poliedros uniformes.
Sopov (1970) demostró su conjetura de que la lista estaba completa.
En 1974, Magnus Wenninger publicó su libro Modelos de poliedros , que enumera los 75 poliedros uniformes no prismáticos, con muchos nombres inéditos que les dio Norman Johnson .
Skilling (1975) demostró de forma independiente la completitud y mostró que si se relaja la definición de poliedro uniforme para permitir que los bordes coincidan, entonces hay sólo una posibilidad extra (el gran dirrombidodecaedro desprovisto de protuberancias ).
En 1987, Edmond Bonan dibujó todos los poliedros uniformes y sus duales en 3D con un programa Turbo Pascal llamado Polyca . La mayoría de ellos fueron mostrados durante el Congreso de la Unión Estereoscópica Internacional celebrado en 1993, en el Teatro del Congreso, Eastbourne, Inglaterra; y nuevamente en 2005 en el Kursaal de Besançon, Francia. ^[5]
En 1993, Zvi Har'El (1949-2008) ^[6] produjo una construcción caleidoscópica completa de los poliedros uniformes y duales con un programa de computadora llamado Kaleido y la resumió en un artículo Solución uniforme para poliedros uniformes , contando las figuras 1 a 80. ^[7]
También en 1993, R. Mäder trasladó esta solución de Kaleido a Mathematica con un sistema de indexación ligeramente diferente. ^[8]
En 2002, Peter W. Messer descubrió un conjunto mínimo de expresiones de forma cerrada para determinar las principales cantidades combinatorias y métricas de cualquier poliedro uniforme (y su dual) dado solo su símbolo de Wythoff . ^[9]

Poliedros estrellados uniformes

Las 57 formas no prismáticas no convexas, con excepción del gran dirrombicosidodecaedro , están compiladas por construcciones de Wythoff dentro de los triángulos de Schwarz .

Formas convexas según la construcción de Wythoff

Los poliedros uniformes convexos pueden nombrarse mediante operaciones de construcción de Wythoff sobre la forma regular.

Con más detalle se muestran a continuación los poliedros uniformes convexos según su construcción Wythoff dentro de cada grupo de simetría.

Dentro de la construcción de Wythoff, hay repeticiones creadas por formas de simetría inferior. El cubo es un poliedro regular y un prisma cuadrado. El octaedro es un poliedro regular y un antiprisma triangular. El octaedro también es un tetraedro rectificado . Muchos poliedros se repiten a partir de diferentes fuentes de construcción y tienen colores diferentes.

La construcción de Wythoff se aplica por igual a poliedros uniformes y teselas uniformes sobre la superficie de una esfera , por lo que se dan imágenes de ambos. Las teselas esféricas incluyen el conjunto de hosoedros y diedros, que son poliedros degenerados.

Estos grupos de simetría se forman a partir de los grupos de puntos de reflexión en tres dimensiones , cada uno representado por un triángulo fundamental ( p q r ), donde p > 1, q > 1, r > 1 y 1/ p + 1/ q + 1/ r < 1 .

Simetría tetraédrica (3 3 2) – orden 24
Simetría octaédrica (4 3 2) – orden 48
Simetría icosaédrica (5 3 2) – orden 120
Simetría diedro ( n 2 2), para n = 3,4,5,... – orden 4 n

Las formas no reflectantes restantes se construyen mediante operaciones de alternancia aplicadas a los poliedros con un número par de lados.

Junto con los prismas y su simetría diedral , el proceso de construcción esférica de Wythoff añade dos clases regulares que se degeneran en poliedros: los diedros y los hosoedros , los primeros con sólo dos caras y los segundos con sólo dos vértices. El truncamiento de los hosoedros regulares crea los prismas.

Debajo de los poliedros uniformes convexos se encuentran los índices 1–18 para las formas no prismáticas tal como se presentan en las tablas por forma de simetría.

Para el conjunto infinito de formas prismáticas, éstas se indexan en cuatro familias:

Hosohedra H _2... (solo como teselación esférica)
Diedros D _2... (solo como teselación esférica)
Prismas P _3... (hosoedros truncados)
Antiprismas A _3... (prismas chatos)

Tablas de resumen

Nombre Johnson	Padre	Truncado	Rectificado	Bittruncado (tr. dual)	Birectificado (doble)	Cantelado	Omnitruncado ( cantitruncado )	Desaire
Diagrama de Coxeter
Símbolo Schläfli extendido	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{p,q}	t{p,q}	r{p,q}	2t{p,q}	2r{p,q}	rr{p,q}	tr{p,q}	sr{p,q}
	t ₀ {p,q}	t _0,1 {p,q}	t1 {p _, q}	t1,2 _{ p,q}	t2 {p _, q}	t _0,2 {p,q}	t _0,1,2 {p,q}	alto _0,1,2 {p,q}
Símbolo de Wythoff (pq 2)	q \| pág. 2	2 q \| p	2 \| pq	2 p \| q	p\|q2	pq \| 2	paquete 2 \|	\| pq 2
Figura de vértice	pq	q.2p.2p	(pq) ²	pág.2q.2q	qp	pág. 4.q.4	4.2p.2q	3.3.p.3.q
Tetraédrica (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
Octaédrico (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
Icosaédrica (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

Y una muestra de simetrías diedras:

(La esfera no se corta, sólo se corta el revestimiento.) (En una esfera, una arista es el arco del círculo máximo, el camino más corto, entre sus dos vértices. Por lo tanto, un dígono cuyos vértices no son polos opuestos es plano: parece una arista.)

(pág. 2 2)	Padre	Truncado	Rectificado	Bittruncado (tr. dual)	Birectificado (doble)	Cantelado	Omnitruncado ( cantitruncado )	Desaire
Diagrama de Coxeter
Símbolo Schläfli extendido	${\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}p,2\end{Bmatrix}}$	${\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}2,p\end{Bmatrix}}$	${\begin{Bmatrix}2,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\2\end{Bmatrix}}$
	{pág. 2}	t{p,2}	r{p,2}	2t{p,2}	2r{p,2}	rr{p,2}	tr{p,2}	sr{p,2}
	t0 {p, ₂ }	t0,1 _{ p,2}	t1 {p _, 2}	t1,2 _{ p,2}	t2 {p _, 2}	t0,2 _{ p,2}	t0,1,2 _{ p,2}	alto _0,1,2 {p,2}
Símbolo de Wythoff	2 \| pág. 2	2 2 \| p	2 \| pág. 2	2 pág. 2	pág \| 2 2	pág. 2 \| 2	pág. 2 2 \|	\| pág. 2 2
Figura de vértice	pág. ²	2,2p.2p.	pág. 2.pág. 2	pág. 4.4	2 ^p	pág. 4.2.4	4.2pág.4	3.3.3.p
Diédrico (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
Diédrico (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	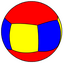4.4.6	3.3.3.3
Diédrico (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	3.3.3.4
Diédrico (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	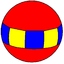4.4.10	3.3.3.5
Diédrico (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

(3 3 2) yo_dsimetría tetraédrica

La simetría tetraédrica de la esfera genera cinco poliedros uniformes y una sexta forma mediante una operación de roce.

La simetría tetraédrica se representa mediante un triángulo fundamental con un vértice con dos espejos y dos vértices con tres espejos, representados por el símbolo (3 3 2). También se puede representar mediante el grupo de Coxeter A ₂ o [3,3], así como mediante un diagrama de Coxeter :.

Hay 24 triángulos, visibles en las caras del tetrakis hexaedro y en los triángulos coloreados alternativamente en una esfera:

#	Nombre	Gráfico A ₃	Gráfico A ₂	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Gráfico A ₃	Gráfico A ₂	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [3] (4)	Pos. 1 [2] (6)	Pos. 0 [3] (4)	Caras	Bordes	Vértices
1	Tetraedro						{3,3}	{3}			4	6	4
[1]	Tetraedro birectificado (igual que tetraedro )						t2 {3,3}={3,3 _}			{3}	4	6	4
2	Tetraedro rectificado Tetratetraedro (igual que octaedro )						t1 _{ 3,3}=r{3,3}	{3}		{3}	8	12	6
3	Tetraedro truncado						t0,1 { _3,3 }=t{3,3}	{6}		{3}	8	18	12
[3]	Tetraedro bitruncado (igual que tetraedro truncado )						t1,2 { _3,3 }=t{3,3}	{3}		{6}	8	18	12
4	Tetraedro cantelado Rombitetratetraedro (igual que cuboctaedro )						t _0,2 {3,3} = rr{3,3}	{3}	{4}	{3}	14	24	12
5	Tetraedro omnitruncado Tetratetraedro truncado (igual que octaedro truncado )						t0,1,2 { _3,3 }=tr{3,3}	{6}	{4}	{6}	14	36	24
6	Tetratetraedro romo (igual que icosaedro )		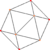				sr{3,3}	{3}	2 {3}	{3}	20	30	12

(4 3 2) O_yosimetría octaédrica

La simetría octaédrica de la esfera genera 7 poliedros uniformes y otros 7 por alternancia. Seis de estas formas se repiten de la tabla de simetría tetraédrica anterior.

La simetría octaédrica se representa mediante un triángulo fundamental (4 3 2) contando los espejos en cada vértice. También se puede representar mediante el grupo de Coxeter B ₂ o [4,3], así como mediante un diagrama de Coxeter :.

Hay 48 triángulos, visibles en las caras del dodecaedro disdyakis y en los triángulos coloreados alternativamente en una esfera:

#	Nombre	Gráfico B ₃	Gráfico B ₂	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Gráfico B ₃	Gráfico B ₂	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [4] (6)	Pos. 1 [2] (12)	Pos. 0 [3] (8)	Caras	Bordes	Vértices
7	Cubo						{4,3}	{4}			6	12	8
[2]	Octaedro						{3,4}			{3}	8	12	6
[4]	Cubo rectificado Octaedro rectificado ( Cuboctaedro )						{4,3}	{4}		{3}	14	24	12
8	Cubo truncado						t0,1 { _4,3 }=t{4,3}	{8}		{3}	14	36	24
[5]	Octaedro truncado						t0,1 { _3,4 }=t{3,4}	{4}		{6}	14	36	24
9	Cubo canteado Octaedro canteado Rombicuboctaedro						t _0,2 {4,3} = rr{4,3}	{4}	{4}	{3}	26	48	24
10	Cubo omnitruncado Octaedro omnitruncado Cuboctaedro truncado						t _0,1,2 {4,3}=tr{4,3}	{8}	{4}	{6}	26	72	48
[6]	Octaedro romo (igual que icosaedro )						= s{3,4}=sr{3,3}		{3}	{3}	20	30	12
[1]	Medio cubo (igual que el tetraedro )						= h{4,3}={3,3}	¹ / ₂ {3}			4	6	4
[2]	Cubo cántico (igual que Tetraedro truncado )						= h2 { _4,3 }=t{3,3}	¹ / ₂ {6}		¹ / ₂ {3}	8	18	12
[4]	(igual que Cuboctaedro )						= rr{3,3}				14	24	12
[5]	(igual que octaedro truncado )						= tr{3,3}				14	36	24
[9]	Octaedro romo cántico (igual que rombicuboctaedro )						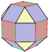s2 _{ 3,4}=rr{3,4}				26	48	24
11	Cuboctaedro romo						sr{4,3}	{4}	2 {3}	{3}	38	60	24

(5 3 2) yo_yosimetría icosaédrica

La simetría icosaédrica de la esfera genera 7 poliedros uniformes y uno más por alternancia. Solo se repite uno de la tabla de simetría tetraédrica y octaédrica anterior.

La simetría icosaédrica se representa mediante un triángulo fundamental (5 3 2) contando los espejos en cada vértice. También se puede representar mediante el grupo de Coxeter G ₂ o [5,3], así como mediante un diagrama de Coxeter :.

Hay 120 triángulos, visibles en las caras del triacontaedro de Disdyakis y en los triángulos coloreados alternativamente en una esfera:

#	Nombre	Gráfica (A ₂ ) [6]	Gráfica (H ₃ ) [10]	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Gráfica (A ₂ ) [6]	Gráfica (H ₃ ) [10]	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [5] (12)	Pos. 1 [2] (30)	Pos. 0 [3] (20)	Caras	Bordes	Vértices
12	Dodecaedro						{5,3}	{5}			12	30	20
[6]	Icosaedro						{3,5}			{3}	20	30	12
13	Dodecaedro rectificado Icosaedro rectificado Icosidodecaedro						t1 { _5,3 }=r{5,3}	{5}		{3}	32	60	30
14	Dodecaedro truncado						t0,1 { _5,3 }=t{5,3}	{10}		{3}	32	90	60
15	Icosaedro truncado		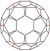				t0,1 { _3,5 }=t{3,5}	{5}		{6}	32	90	60
16	Dodecaedro cantelado Icosaedro cantelado Rombicosidodecaedro						t _0,2 {5,3} = rr{5,3}	{5}	{4}	{3}	62	120	60
17	Dodecaedro omnitruncado Icosaedro omnitruncado Icosidodecaedro truncado						t0,1,2 { _5,3 }=tr{5,3}	{10}	{4}	{6}	62	180	120
18	Icosidodecaedro romo						sr{5,3}	{5}	2 {3}	{3}	92	150	60

(p 2 2) Prismático [p,2], yo₂(p) familia (D_pHsimetría diedro)

La simetría diedro de la esfera genera dos conjuntos infinitos de poliedros uniformes, prismas y antiprismas, y dos conjuntos infinitos más de poliedros degenerados, los hosoedros y diedros, que existen como teselaciones en la esfera.

La simetría diedral se representa mediante un triángulo fundamental (p 2 2) contando los espejos en cada vértice. También se puede representar mediante el grupo de Coxeter I ₂ (p) o [n,2], así como mediante un diagrama prismático de Coxeter :.

A continuación se muestran las primeras cinco simetrías diedras: D ₂ ... D ₆ . La simetría diedral D _p tiene orden 4n , representada por las caras de una bipirámide , y en la esfera como una línea ecuatorial en la longitud n líneas de longitud igualmente espaciadas.

(2 2 2) Simetría diedra

Hay 8 triángulos fundamentales, visibles en las caras de la bipirámide cuadrada (octaedro) y triángulos coloreados alternativamente en una esfera:

#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [2] (2)	Pos. 1 [2] (2)	Pos. 0 [2] (2)	Caras	Bordes	Vértices
D2H2	Diedro digonal , hosoedro digonal				{2,2}	{2}			2	2	2
D4	Diedro diagonal truncado (igual que diedro cuadrado )				t{2,2}={4,2}	{4}			2	4	4
Pág. ₄ [7]	Diedro digonal omnitruncado (igual que el cubo )				t _0,1,2 {2,2} = tr{2,2}	{4}	{4}	{4}	6	12	8
Un ₂ [1]	Diedro diagonal romo (igual que tetraedro )				sr{2,2}		2 {3}		4	6	4

(3 2 2) el_{3 horas}simetría diedro

Hay 12 triángulos fundamentales, visibles en las caras de la bipirámide hexagonal y triángulos coloreados alternativamente en una esfera:

#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [3] (2)	Pos. 1 [2] (3)	Pos. 0 [2] (3)	Caras	Bordes	Vértices
D3	Diedro trigonal				{3,2}	{3}			2	3	3
H3	Hosoedro trigonal				{2,3}			{2}	3	3	2
D6	Diedro trigonal truncado (igual que diedro hexagonal )				t{3,2}	{6}			2	6	6
Pág. ₃	Prisma triangular ( hosoedro trigonal truncado )				t{2,3}	{3}	{4}		5	9	6
Pág. ₆	Diedro trigonal omnitruncado ( prisma hexagonal )				t0,1,2 { _2,3 }=tr{2,3}	{6}	{4}	{4}	8	18	12
Un ₃ [2]	Diedro trigonal romo (igual que antiprisma triangular ) (igual que octaedro )				sr{2,3}	{3}	2 {3}		8	12	6
Pág. ₃	Diedro trigonal romo cántico ( prisma triangular )				s2 {2,3}=t{2,3 _}				5	9	6

(4 2 2) el_{4 horas}simetría diedro

Hay 16 triángulos fundamentales, visibles en las caras de la bipirámide octogonal y triángulos coloreados alternativamente en una esfera:

#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [4] (2)	Pos. 1 [2] (4)	Pos. 0 [2] (4)	Caras	Bordes	Vértices
D4	diedro cuadrado				{4,2}	{4}			2	4	4
H4	hosoedro cuadrado				{2,4}			{2}	4	4	2
D8	Diedro cuadrado truncado (igual que diedro octogonal )				t{4,2}	{8}			2	8	8
Pág. ₄ [7]	Hosoedro cuadrado truncado ( Cubo )				t{2,4}	{4}	{4}		6	12	8
D8	Diedro cuadrado omnitruncado ( prisma octogonal )				t0,1,2 { _2,4 }=tr{2,4}	{8}	{4}	{4}	10	24	16
Un ₄	Diedro cuadrado romo ( antiprisma cuadrado )				sr{2,4}	{4}	2 {3}		10	16	8
Pág. ₄ [7]	Diedro cuadrado romo cántico ( Cubo )				s2 {4,2}=t{2,4 _}				6	12	8
Un ₂ [1]	Hosoedro cuadrado romo ( antiprisma diagonal ) ( tetraedro )				s{2,4}=sr{2,2}				4	6	4

(5 2 2) D_{5 horas}simetría diedro

Hay 20 triángulos fundamentales, visibles en las caras de la bipirámide decagonal y triángulos coloreados alternativamente en una esfera:

#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [5] (2)	Pos. 1 [2] (5)	Pos. 0 [2] (5)	Caras	Bordes	Vértices
D5	Diedro pentagonal				{5,2}	{5}			2	5	5
H5	Hosoedro pentagonal				{2,5}			{2}	5	5	2
D10	Diedro pentagonal truncado (igual que diedro decagonal )				t{5,2}	{10}			2	10	10
Pág. ₅	Hosoedro pentagonal truncado (igual que prisma pentagonal )				t{2,5}	{5}	{4}		7	15	10
Pág. ₁₀	Diedro pentagonal omnitruncado ( prisma decagonal )				t0,1,2 { _2,5 }=tr{2,5}	{10}	{4}	{4}	12	30	20
Un ₅	Diedro pentagonal romo ( antiprisma pentagonal )				sr{2,5}	{5}	2 {3}		12	20	10
Pág. ₅	Diedro pentagonal chato cántico ( Prisma pentagonal )				s2 {5,2}=t{2,5 _}				7	15	10

(6 2 2) D_{6 horas}simetría diedro

Hay 24 triángulos fundamentales, visibles en las caras de la bipirámide dodecagonal y triángulos coloreados alternativamente en una esfera.

#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Recuento de rostros por posición			Recuento de elementos
#	Nombre	Imagen	Embaldosado	Figura de vértice	Símbolos de Coxeter y Schläfli	Pos. 2 [6] (2)	Pos. 1 [2] (6)	Pos. 0 [2] (6)	Caras	Bordes	Vértices
D6	Diedro hexagonal				{6,2}	{6}			2	6	6
H6	Hosoedro hexagonal				{2,6}			{2}	6	6	2
D ₁₂	Diedro hexagonal truncado (igual que diedro dodecagonal )				t{6,2}	{12}			2	12	12
H6	Hosoedro hexagonal truncado (igual que prisma hexagonal )				t{2,6}	{6}	{4}		8	18	12
Pág. ₁₂	Diedro hexagonal omnitruncado ( prisma dodecagonal )				t0,1,2 { _2,6 }=tr{2,6}	{12}	{4}	{4}	14	36	24
Un ₆	Diedro hexagonal romo ( antiprisma hexagonal )				sr{2,6}	{6}	2 {3}		14	24	12
Pág. ₃	Diedro hexagonal cántico ( prisma triangular )				= h2 {6,2}=t{2,3 _}				5	9	6
Pág. ₆	Diedro hexagonal romo cántico ( Prisma hexagonal )				s2 {6,2}=t{2,6 _}				8	18	12
Un ₃ [2]	Hosoedro hexagonal romo (igual que antiprisma triangular ) (igual que octaedro )				s{2,6}=sr{2,3}				8	12	6

Operadores de construcción de Wythoff

Operación	Símbolo	Descripción
Padre	{p,q} t ₀ {p,q}	Cualquier poliedro regular o teselacion
Rectificado (r)	r{p,q} t ₁ {p,q}	Las aristas se truncan por completo en puntos únicos. El poliedro ahora tiene las caras combinadas del padre y del dual. Los poliedros se nombran según el número de lados de las dos formas regulares: {p,q} y {q,p}, como el cuboctaedro para r{4,3} entre un cubo y un octaedro.
Birectificado (2r) (también dual )	2r{p,q} t ₂ {p,q}	La birectificación (dual) es un truncamiento adicional, de modo que las caras originales se reducen a puntos. Se forman nuevas caras debajo de cada vértice principal. El número de aristas no cambia y se rotan 90 grados. Una birectificación puede considerarse como dual.
Truncado (t)	t{p,q} t _0,1 {p,q}	Cada vértice original se corta y una nueva cara llena el espacio vacío. El truncamiento tiene un grado de libertad, que tiene una solución que crea un poliedro truncado uniforme. El poliedro tiene sus caras originales duplicadas en lados y contiene las caras del dual.
Bitruncado (2t) (también dual truncado)	2t{p,q} t _1,2 {p,q}	Un bitruncado puede considerarse como el truncamiento del dual. Un cubo bitruncado es un octaedro truncado.
Cantelated (rr) (También expandido )	rr{p,q}	Además del truncamiento de vértices, cada arista original se bisela y aparecen nuevas caras rectangulares en su lugar. Una cantelación uniforme se encuentra a medio camino entre las formas padre y dual. Un poliedro cantelado se denomina rombi-r{p,q}, como el rombicuboctaedro para rr{4,3}.
Cantitruncado (tr) (También omnitruncado )	tr{p,q} t _0,1,2 {p,q}	Las operaciones de truncamiento y cantelación se aplican juntas para crear una forma omnitruncada que tiene las caras del padre duplicadas en los lados, las caras del dual duplicadas en los lados y cuadrados donde existían los bordes originales.

Operaciones de alternancia
Operación	Símbolo	Descripción
Snub rectificado (sr)	sr{p,q}	Los cantitruncados alternados. Todas las caras originales acaban teniendo la mitad de lados y los cuadrados degeneran en aristas. Como las formas omnitruncadas tienen 3 caras/vértice, se forman nuevos triángulos. Normalmente, estas formas de facetado alternado se deforman ligeramente después para acabar de nuevo como poliedros uniformes. La posibilidad de esta última variación depende del grado de libertad.
Desaire(s)	s{p,2q}	Truncamiento alterno
Desaire cántico (s ₂ )	s2 {p _, 2q}
Cantelación alternada (hrr)	hrr{2p,2q}	Sólo es posible en teselaciones uniformes (poliedros infinitos), alternancia de Por ejemplo,
mitad (h)	h{2p,q}	Alternancia de, lo mismo que
Cántico (h ₂ )	h2 {2p _, q}	Lo mismo que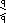
Rectificado a la mitad (hr)	hora{2p,2q}	Sólo es posible en teselaciones uniformes (poliedros infinitos), alternancia de, lo mismo queo Por ejemplo,=o
Cuarto (q)	q{2p,2q}	Sólo es posible en teselados uniformes (poliedros infinitos), lo mismo que Por ejemplo,=o

Véase también

Notas

^ Diudea (2018), pág. https://books.google.com/books?id=p_06DwAAQBAJ&pg=PA4040].
^ Coxeter, Longuet-Higgins y Miller (1954).
^ Politopos regulares, p.13
^ Poliedros de Piero della Francesca
^ Edmond Bonan, "Polyèdres Eastbourne 1993", Stéréo-Club Français 1993
^ Dr. Zvi Har'El (14 de diciembre de 1949 – 2 de febrero de 2008) y Estudios internacionales sobre Julio Verne: un homenaje
^ Har'el, Zvi (1993). "Solución uniforme para poliedros uniformes" (PDF) . Geometriae Dedicata . 47 : 57-110. doi : 10.1007/BF01263494 .Zvi Har'El, software Kaleido, Imágenes, imágenes duales
^ Mäder, RE Poliedros uniformes. Mathematica J. 3, 48-57, 1993. [1]
^ Messer, Peter W. (2002). "Expresiones de forma cerrada para poliedros uniformes y sus duales". Geometría discreta y computacional . 27 (3): 353–375. doi : 10.1007/s00454-001-0078-2 .

Referencias

Brückner, M. Vielecke und vielflache. Theorie und geschichte. . Leipzig, Alemania: Teubner, 1900. [2]
Coxeter, Harold Scott MacDonald ; Longuet-Higgins, MS ; Miller, JCP (1954). "Poliedros uniformes" (PDF) . Philosophical Transactions of the Royal Society A . 246 (916): 401–450. Bibcode :1954RSPTA.246..401C. doi :10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183.
Diudea, MV (2018), Cúmulos poliédricos de múltiples capas, Springer , doi :10.1007/978-3-319-64123-2, ISBN 978-3-319-64123-2
Grünbaum, B. (1994), "Poliedros con caras huecas", en Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. (eds.), Actas del Instituto de Estudios Avanzados de la OTAN sobre politopos: Resumen, convexo y computacional , Springer, págs. 43–70, doi :10.1007/978-94-011-0924-6_3, ISBN 978-94-010-4398-4
McMullen, Peter ; Schulte, Egon (2002), Resumen de politopos regulares , Cambridge University Press
Skilling, J. (1975). "El conjunto completo de poliedros uniformes". Philosophical Transactions of the Royal Society of London. Serie A. Ciencias matemáticas y físicas . 278 (1278): 111–135. Bibcode :1975RSPTA.278..111S. doi :10.1098/rsta.1975.0022. ISSN 0080-4614. JSTOR 74475. MR 0365333. S2CID 122634260.
Sopov, SP (1970). "Una prueba de la completitud de la lista de poliedros homogéneos elementales". Ukrainskiui Geometricheskiui Sbornik (8): 139–156. MR 0326550.
Wenninger, Magnus (1974). Modelos de poliedros . Cambridge University Press. ISBN 978-0-521-09859-5.

Enlaces externos

Weisstein, Eric W. "Poliedro uniforme". MathWorld .
Solución uniforme para poliedros uniformes
Los poliedros uniformes
Poliedros virtuales Poliedros uniformes
Galería de poliedros uniformes
Poliedro uniforme - de Wolfram MathWorld Tiene un gráfico visual de los 75

en a mi Politopos fundamentales convexos regulares y uniformes en dimensiones 2–10
Familia	Un	Bn	Yo ₂ (p) / D _n	Mi ₆ / Mi ₇ / Mi ₈ / Fa ₄ / Sol ₂	H- _n
Polígono regular	Triángulo	Cuadrado	p-gon	Hexágono	Pentágono
Poliedro uniforme	Tetraedro	Octaedro • Cubo	Semicubo		Dodecaedro • Icosaedro
Policoron uniforme	Pentachoron	16 celdas • Tesseract	Acto de Demitesseract	24 celdas	120 celdas • 600 celdas
Politopo 5 uniforme	5-símplex	5-ortoplex • 5-cubo	5-demicubes
Politopo uniforme de 6 elementos	6-símplex	6-ortoplex • 6-cubo	6-demicubes	1 ₂₂ • 2 ₂₁
Politopo 7 uniforme	7-símplex	7-ortoplex • 7-cubo	7-demicube	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Politopo 8 uniforme	8-símplex	8-ortoplex • 8-cubo	8-demicubes	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Politopo uniforme de 9 capas	9-símplex	9-ortoplex • 9-cubo	9-demicubes
Politopo uniforme de 10	10-símplex	10-ortoplex • 10-cubo	10-demicubes
Politopo uniforme n	n - símplex	n - ortoplex • n - cubo	n - demicubo	1 _k2 • 2 _k1 • k21	n - politopo pentagonal
Temas: Familias de politopos • Politopo regular • Lista de politopos regulares y compuestos

[FOOTNOTEDiudea2018https://books.google.com/books?id=p_06DwAAQBAJ&pg=PA40_40]-1] Diudea (2018), pág. https://books.google.com/books?id=p_06DwAAQBAJ&pg=PA4040].

[FOOTNOTECoxeterLonguet-HigginsMiller1954-2] Coxeter, Longuet-Higgins y Miller (1954).

[3] Politopos regulares, p.13

[4] Poliedros de Piero della Francesca

[5] Edmond Bonan, "Polyèdres Eastbourne 1993", Stéréo-Club Français 1993

[6] Dr. Zvi Har'El (14 de diciembre de 1949 – 2 de febrero de 2008) y Estudios internacionales sobre Julio Verne: un homenaje

[7] Har'el, Zvi (1993). "Solución uniforme para poliedros uniformes" (PDF) . Geometriae Dedicata . 47 : 57-110. doi : 10.1007/BF01263494 .Zvi Har'El, software Kaleido, Imágenes, imágenes duales

[8] Mäder, RE Poliedros uniformes. Mathematica J. 3, 48-57, 1993. [1]

[9] Messer, Peter W. (2002). "Expresiones de forma cerrada para poliedros uniformes y sus duales". Geometría discreta y computacional . 27 (3): 353–375. doi : 10.1007/s00454-001-0078-2 .