Lista de modelos de poliedros de Wenninger

Esta es una lista indexada de los poliedros uniformes y estrellados del libro Polyhedron Models , de Magnus Wenninger .

El libro fue escrito como una guía para construir poliedros como modelos físicos. Incluye plantillas de elementos de caras para la construcción y consejos útiles para la construcción, así como breves descripciones sobre la teoría detrás de estas formas. Contiene los 75 poliedros uniformes no prismáticos , así como 44 formas esteladas de los poliedros convexos regulares y cuasirregulares.

Los modelos enumerados aquí se pueden citar como "Número de modelo Wenninger N ", o W _N para abreviar.

Los poliedros se agrupan en 5 tablas: regulares (1–5), semirregulares (6–18), poliedros estrella regulares (20–22,41), estelaciones y compuestos (19–66) y poliedros estrella uniformes (67–119). Los cuatro poliedros estrella regulares se enumeran dos veces porque pertenecen tanto a la agrupación de poliedros uniformes como a la de estelaciones.

Índice	Nombre	Imagen	Nombre dual	Imagen dual	Símbolo de Wythoff	Figura de vértice y símbolo de Schläfli	Grupo de simetría	Tú #	K#	V	mi	F	Caras por tipo
1	Tetraedro		Tetraedro		3|2 3	{3,3}	T.D.​	U01	K06	4	6	4	4{3}
2	Octaedro		Hexaedro		4|2 3	{3,4}	Oh​	U05	K10	6	12	8	8{3}
3	Hexaedro (cubo)		Octaedro		3|2 4	{4,3}	Oh​	U06	K11	8	12	6	6{4}
4	Icosaedro		Dodecaedro		5|2 3	{3,5}	Yo soy	U22	K27	12	30	20	20{3}
5	Dodecaedro		Icosaedro		3|2 5	{5,3}	Yo soy	U23	K28	20	30	12	12{5}

Índice	Nombre	Imagen	Nombre dual	Imagen dual	Símbolo de Wythoff	Figura de vértice	Grupo de simetría	Tú #	K#	V	mi	F	Caras por tipo
6	Tetraedro truncado		triakis tetraedro		2 3|3	3.6.6	T.D.​	U02	K07	12	18	8	4{3} + 4{6}
7	Octaedro truncado		tetrakis hexaedro		2 4|3	4.6.6	Oh​	U08	K13	14	36	24	6{4} + 8{6}
8	Hexaedro truncado		triakis octaedro		2 3|4	3.8.8	Oh​	U09	K14	24	36	14	8{3} + 6{8}
9	Icosaedro truncado		Dodecaedro pentakis		2 5|3	5.6.6	Yo soy	U25	K30	60	90	32	12{5} + 20{6}
10	Dodecaedro truncado		triakisicosaedro		2 3|5	3.10.10	Yo soy	U26	K31	60	90	32	20{3} + 12{10}
11	Cuboctaedro		dodecaedro rómbico		2|3 4	3.4.3.4	Oh​	U07	K12	12	24	14	8{3} + 6{4}
12	Icosidodecaedro		triacontaedro rómbico		2|3 5	3.5.3.5	Yo soy	U24	K29	30	60	32	20{3} + 12{5}
13	Pequeño rombicuboctaedro		icositetraedro deltoidal		3 4|2	3.4.4.4	Oh​	U10	K15	24	48	26	8{3}+(6+12){4}
14	Pequeño rombicosidodecaedro		hexecontaedro deltoidal		3 5|2	3.4.5.4	Yo soy	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	Cuboctaedro truncado (Gran rombicuboctaedro)		Dodecaedro de Disdyakis		2 3 4|	4.6.8	Oh​	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	Icosidodecaedro truncado (Gran rombicosidodecaedro)		Triacontaedro de Disdyakis		2 3 5|	4.6.10	Yo soy	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	Cubo de snub		icositetraedro pentagonal		|2 3 4	3.3.3.3.4	Oh	U12	K17	24	60	38	(8 + 24){3} + 6{4}
18	Dodecaedro romo		hexecontaedro pentagonal		|2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60){3} + 12{5}

Índice	Nombre	Imagen	Nombre dual	Imagen dual	Símbolo de Wythoff	Figura de vértice y símbolo de Schläfli	Grupo de simetría	Tú #	K#	V	mi	F	Caras por tipo
20	Pequeño dodecaedro estrellado		Gran dodecaedro		5|2 5 / 2	{ 5 / 2 ,5}	Yo soy	U34	K39	12	30	12	12{ 5 / 2 }
21	Gran dodecaedro		Pequeño dodecaedro estrellado		5 / 2 | 2 5	{5, 5 / 2 }	Yo soy	U35	K40	12	30	12	12{5}
22	Gran dodecaedro estrellado		Gran icosaedro		3|2 5 / 2	{ 5 / 2 ,3}	Yo soy	U52	K57	20	30	12	12{ 5 / 2 }
41	Gran icosaedro (16ª estelación del icosaedro)		Gran dodecaedro estrellado		5 / 2 | 2 3	{3, 5 / 2 }	Yo soy	U53	K58	12	30	20	20{3}

Índice	Nombre	Grupo de simetría	Imagen	Facetas
2	Octaedro (regular)	Oh​
19	Octaedro estrellado (compuesto de dos tetraedros)	Oh​

Índice	Nombre	Grupo de simetría	Imagen	Facetas
5	Dodecaedro (regular)	Yo soy
20	Pequeño dodecaedro estrellado (regular) (Primera estelación del dodecaedro)	Yo soy
21	Gran dodecaedro (regular) (Segunda estelación del dodecaedro)	Yo soy
22	Gran dodecaedro estrellado (regular) (Tercera estelación del dodecaedro)	Yo soy

Índice	Nombre	Grupo de simetría	Imagen	Facetas
4	Icosaedro (regular)	Yo soy
23	Compuesto de cinco octaedros (Primera estelación compuesta del icosaedro)	Yo soy
24	Compuesto de cinco tetraedros (Segunda estelación compuesta del icosaedro)	I
25	Compuesto de diez tetraedros (Tercera estelación compuesta del icosaedro)	Yo soy
26	Pequeño icosaedro triámbico (Primera estelación del icosaedro) ( Triakisicosaedro )	Yo soy
27	Segunda estelación del icosaedro	Yo soy
28	Dodecaedro excavado (Tercera estelación del icosaedro)	Yo soy
29	Cuarta estelación del icosaedro	Yo soy
30	Quinta estelación del icosaedro	Yo soy
31	Sexta estelación del icosaedro	Yo soy
32	Séptima estelación del icosaedro	Yo soy
33	Octava estelación del icosaedro	Yo soy
34	Novena estelación del icosaedro Gran icosaedro triámbico	Yo soy
35	Décima estelación del icosaedro	I
36	Undécima estelación del icosaedro	I
37	Duodécima estelación del icosaedro	Yo soy
38	Decimotercera estelación del icosaedro	I
39	Decimocuarta estelación del icosaedro	I
40	Decimoquinta estelación del icosaedro	I
41	Gran icosaedro (regular) (Decimosexta estelación del icosaedro)	Yo soy
42	Estelación final del icosaedro	Yo soy

Índice	Nombre	Grupo de simetría	Imagen	Facetas (planos octaédricos)	Facetas (planos del cubo)
11	Cuboctaedro (regular)	Oh​
43	Compuesto de cubo y octaedro (Primera estelación del cuboctaedro)	Oh​
44	Segunda estelación del cuboctaedro	Oh​
45	Tercera estelación del cuboctaedro	Oh​
46	Cuarta estelación del cuboctaedro	Oh​

Índice	Nombre	Grupo de simetría	Imagen	Facetas (planos icosaédricos)	Facetas (planos dodecaédricos)
12	Icosidodecaedro (regular)	Yo soy
47	(Primera estelación del icosidodecaedro) Compuesto de dodecaedro e icosaedro	Yo soy
48	Segunda estelación del icosidodecaedro	Yo soy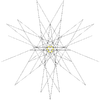
49	Tercera estelación del icosidodecaedro	Yo soy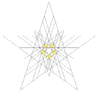
50	Cuarta estelación del icosidodecaedro (Compuesto de un pequeño dodecaedro estrellado y un triakisicosaedro)	Yo soy
51	Quinta estelación del icosidodecaedro (Compuesto de un pequeño dodecaedro estrellado y cinco octaedros)	Yo soy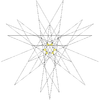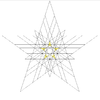
52	Sexta estelación del icosidodecaedro	Yo soy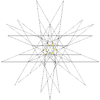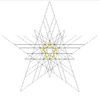
53	Séptima estelación del icosidodecaedro	Yo soy
54	Octava estelación del icosidodecaedro (Compuesto de cinco tetraedros y gran dodecaedro)	I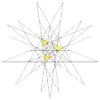
55	Novena estelación del icosidodecaedro	Yo soy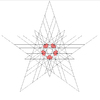
56	Décima estelación del icosidodecaedro	Yo soy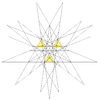
57	Undécima estelación del icosidodecaedro	Yo soy
58	Duodécima estelación del icosidodecaedro	Yo soy
59	Decimotercera estelación del icosidodecaedro	Yo soy
60	Decimocuarta estelación del icosidodecaedro	Yo soy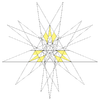
61	Compuesto de gran dodecaedro estrellado y gran icosaedro	Yo soy
62	Decimoquinta estelación del icosidodecaedro	Yo soy
63	Decimosexta estelación del icosidodecaedro	Yo soy
64	Decimoséptima estelación del icosidodecaedro	Yo soy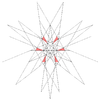
65	Decimoctava estelación del icosidodecaedro	Yo soy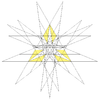
66	Decimonovena estelación del icosidodecaedro	Yo soy

Índice	Nombre	Imagen	Nombre dual	Imagen dual	Símbolo de Wythoff	Figura de vértice	Grupo de simetría	Tú #	K#	V	mi	F	Caras por tipo
67	Tetrahemihexaedro		Tetrahemihexacrón		3 / 2 3|2	4. 3 / 2 .4.3	T.D.​	U04	K09	6	12	7	4{3}+3{4}
68	Octahemioctaedro		Octahemioctacrón		3 / 2 3|3	6.3 / 2 .6.3​	Oh​	U03	K08	12	24	12	8{3}+4{6}
69	Cuboctaedro pequeño		Pequeño icositetraedro hexacrónico		3 / 2 4|4	8. 3 / 2 .8.4	Oh​	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	Icosidodecaedro ditrigonal pequeño		Icosaedro triámbico pequeño		3| 5 / 2 3	( 5 / 2 .3) 3	Yo soy	U30	K35	20	60	32	20{3}+12{ 5 / 2 }
71	Pequeño icosicosidodecaedro		Pequeño hexecontaedro icosacrónico		5 / 2 3|3	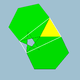6. 5 / 2 .6.3	Yo soy	U31	K36	60	120	52	20{3}+12{ 5 / 2 }+20{6}
72	Dodecicosidodecaedro pequeño		Hexecontaedro dodecacrónico pequeño		3 / 2 5|5	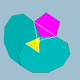10. 3 / 2 .10.5	Yo soy	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	Dodecadodecaedro		Triacontaedro rómbico medial		2| 5 / 2 5	( 5 / 2 .5) 2	Yo soy	U36	K41	30	60	24	12{5}+12{ 5 / 2 }
74	Pequeño rombidodecaedro		Pequeño rombidodecacrón		2 5 / 2 5|	10.4.10 / 9.4 / 3​​​	Yo soy	U39	K44	60	120	42	30{4}+12{10}
75	Gran dodecaedro truncado		Pequeño dodecaedro de stellapentakis		2 5 / 2 |5	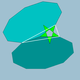10.10.5 / 2​	Yo soy	U37	K42	60	90	24	12{ 5 / 2 }+12{10}
76	Rombidodecadodecaedro		Hexecontaedro deltoidal medial		5 / 2 5|2	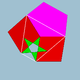4. 5 / 2 .4.5	Yo soy	U38	K43	60	120	54	30{4}+12{5}+12{ 5 / 2 }
77	Gran cuboctaedro cúbico		Gran icositetraedro hexacrónico		3 4| 4 / 3	8 / 3 .3. 8 / 3 .4	Oh​	U14	K19	24	48	20	8{3}+6{4}+6{ 8 / 3 }
78	Cubohemioctaedro		Hexahemioctacrón		4 / 3 4|3	6. 4 / 3 .6.4	Oh​	U15	K20	12	24	10	6{4}+4{6}
79	Cuboctaedro cubituncado (Cuboctaedro cuboctatruncado)		Hexaedro tetradyakis		4 / 3 3 4|	8 / 3.6.8​	Oh​	U16	K21	48	72	20	8{6}+6{8}+6{ 8 / 3 }
80	Dodecadodecaedro ditrigonal		Icosaedro triámbico medial		3| 5 / 3 5	( 5 / 3 .5) 3	Yo soy	U41	K46	20	60	24	12{5}+12{ 5 / 2 }
81	Gran dodecicosidodecaedro ditrigonal		Gran hexecontaedro dodecacrónico ditrigonal		3 5| 5 / 3	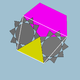10 / 3 .3. 10 / 3 .5	Yo soy	U42	K47	60	120	44	20{3}+12{5}+12{ 10 / 3 }
82	Dodecicosidodecaedro ditrigonal pequeño		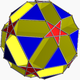Pequeño hexecontaedro dodecacrónico ditrigonal		5 / 3 3|5	10. 5 / 3 .10.3	Yo soy	U43	K48	60	120	44	20{3}+12{ 5 / 2 }+12{10}
83	Icosidodecadodecaedro		Hexecontaedro icosacrónico medial		5 / 3 5|3	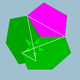6. 5 / 3 .6.5	Yo soy	U44	K49	60	120	44	12{5}+12{ 5 / 2 }+20{6}
84	Dodecadodecaedro icositruncado (icosidodecatruncado icosidodecaedro)		Icosaedro de Tridyakis		5 / 3 3 5|	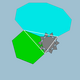10 / 3.6.10​	Yo soy	U45	K50	120	180	44	20{6}+12{10}+12{ 10 / 3 }
85	Gran rombicuboctaedro no convexo (cuasirombicuboctaedro)		Gran icositetraedro deltoidal		3 / 2 4|2	4. 3 / 2 .4.4	Oh​	U17	K22	24	48	26	8{3}+(6+12){4}
86	Pequeño rombihexaedro		Pequeño rombihexacrón		3 / 2 2 4|	4.8.4 / 3.8​​	Oh​	Sub-18	K23	24	48	18	12{4}+6{8}
87	Gran icosidodecaedro ditrigonal		Gran icosaedro triámbico		3 / 2 | 3 5	(5.3.5.3.5.3)/ 2	Yo soy	U47	K52	20	60	32	20{3}+12{5}
88	Gran icosicosidodecaedro		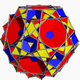Gran hexecontaedro icosacrónico		3 / 2 5|3	6. 3 / 2 .6.5	Yo soy	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	Icosihemidodecaedro pequeño		Icosihemidodecacrón pequeño		3 / 2 3|5	10. 3 / 2 .10.3	Yo soy	U49	K54	30	60	26	20{3}+6{10}
90	Dodecicosaedro pequeño		Dodecicosacrón pequeño		3 / 2 3 5|	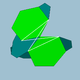10.6.10 / 9.6 / 5​​​	Yo soy	U50	K55	60	120	32	20{6}+12{10}
91	Dodecahemidodecaedro pequeño		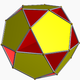Dodecahemidodecacrón pequeño		5 / 4 5|5	10. 5 / 4 .10.5	Yo soy	U51	K56	30	60	18	12{5}+6{10}
92	Hexaedro truncado estrellado (Hexaedro cuasitruncado)		Gran triakis octaedro		2 3| 4 / 3	8/3 . 8 / 3.3​​​	Oh​	Sub-19	K24	24	36	14	8{3}+6{ 8 / 3 }
93	Gran cuboctaedro truncado (Cuboctaedro cuasitruncado)		Gran dodecaedro de Disdyakis		4 / 3 2 3|	8 / 3.4.6​	Oh​	U20	K25	48	72	26	12{4}+8{6}+6{ 8 / 3 }
94	Gran icosidodecaedro		Gran triacontaedro rómbico		2| 5 / 2 3	( 5 / 2 .3) 2	Yo soy	U54	K59	30	60	32	20{3}+12{ 5 / 2 }
95	Gran icosaedro truncado		Gran dodecaedro de stellapentakis		2 5 / 2 |3	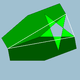6.6.5 / 2​	Yo soy	U55	K60	60	90	32	12{ 5 / 2 }+20{6}
96	rombicosaedro		Rombosacrón		2 5 / 2 3|	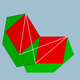6.4.6 / 5 . 4 / 3​	Yo soy	U56	K61	60	120	50	30{4}+20{6}
97	Dodecaedro truncado estrellado pequeño (Dodecaedro estrellado pequeño cuasitruncado)		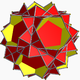Gran pentakis dodecaedro		2 5| 5 / 3	10/3 . 10 / 3.5​​​	Yo soy	U58	K63	60	90	24	12{5}+12{ 10 / 3 }
98	Dodecadodecaedro truncado (Dodecaedro cuasitruncado)		Triacontaedro disdyakis medial		5 / 3 2 5|	10 / 3.4.10​	Yo soy	U59	K64	120	180	54	30{4}+12{10}+12{ 10 / 3 }
99	Gran dodecicosidodecaedro		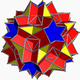Gran hexecontaedro dodecacrónico		5 / 2 3| 5 / 3	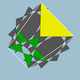10 / 3 . 5 / 2 . 10 / 3 .3	Yo soy	U61	K66	60	120	44	20{3}+12{ 5 / 2 }+12{ 10 / 3 }
100	Dodecaedro hemicosaedro pequeño		Dodecahemicosacrón pequeño		5 / 3 5 / 2 |3	6. 5 / 3 .6. 5 / 2	Yo soy	U62	K67	30	60	22	12{ 5 / 2 }+10{6}
101	Gran dodecicosaedro		Gran dodecicosacrón		5 / 3 5 / 2 3|	6. 10 / 3 . 6 / 5 . 10 / 7	Yo soy	U63	K68	60	120	32	20{6}+12{ 10 / 3 }
102	Gran dodecahemicosaedro		Gran dodecahemicosacrón		5 / 4 5|3	6. 5 / 4 .6.5	Yo soy	U65	K70	30	60	22	12{5}+10{6}
103	Gran rombihexaedro		Gran rombihexacrón		4 / 3 3 / 2 2|	4. 8 / 3 . 4 / 3 . 8 / 5	Oh​	Sub-21	K26	24	48	18	12{4}+6{ 8 / 3 }
104	Gran dodecaedro estrellado truncado (Gran dodecaedro estrellado cuasitruncado)		Gran triakis icosaedro		2 3| 5 / 3	10 / 3 . 10 / 3 .3	Yo soy	U66	K71	60	90	32	20{3}+12{ 10 / 3 }
105	Gran rombicosidodecaedro no convexo (cuasirombicosidodecaedro)		Gran hexecontaedro deltoidal		5 / 3 3|2	4. 5 / 3 .4.3	Yo soy	U67	K72	60	120	62	20{3}+30{4}+12{ 5 / 2 }
106	Gran icosihemidodecaedro		Gran icosihemidodecacrón		3 3| 5 / 3	10 / 3 . 3 / 2 . 10 / 3 .3	Yo soy	U71	K76	30	60	26	20{3}+6{ 10 / 3 }
107	Gran dodecahemidodecaedro		Gran dodecahemidodecacrón		5 / 3 5 / 2 | 5 / 3	10/3 .​​ 5/3 .​​ 10/3 .​​ 5/2​​	Yo soy	U70	K75	30	60	18	12{ 5 / 2 }+6{ 10 / 3 }
108	Gran icosidodecaedro truncado (Gran icosidodecaedro cuasitruncado)		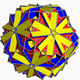Gran triacontaedro de Disdyakis		5 / 3 2 3|	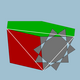10 / 3 .4.6	Yo soy	U68	K73	120	180	62	30{4}+20{6}+12{ 10 / 3 }
109	Gran rombidodecaedro		Gran rombidodecacrón		3 / 2 5 / 3 2|	4. 10 / 3 . 4 / 3 . 10 / 7	Yo soy	U73	K78	60	120	42	30{4}+12{ 10 / 3 }
110	Icosicosidodecaedro romo pequeño		Hexecontaedro hexagonal pequeño		| 5 / 2 3 3	3.3.3.3.3.5 / 2​	Yo soy	U32	K37	60	180	112	(40+60){3}+12{ 5 / 2 }
111	Dodecadodecaedro romo		Hexecontaedro pentagonal medial		|2 5 / 2 5	3.3.5 / 2.3.5​​	I	U40	K45	60	150	84	60{3}+12{5}+12{ 5 / 2 }
112	Icosidodecadodecaedro romo		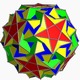Hexecontaedro hexagonal medial		| 5 / 3 3 5	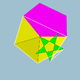3.3.3.3.5.5 / 3​	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{ 5 / 2 }
113	Gran icosidodecaedro romo invertido		Gran hexecontaedro pentagonal invertido		| 5 / 3 2 3	3.3.3.3.5 / 3​	I	U69	K74	60	150	92	(20+60){3}+12{ 5 / 2 }
114	Dodecadodecaedro romo invertido		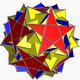Hexecontaedro pentagonal invertido medial		| 5 / 3 2 5	3. 5 / 3 .3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{ 5 / 2 }
115	Gran dodecicosidodecaedro romo		Gran hexecontaedro hexagonal		| 5 / 3 5 / 2 3	3. 5 / 3 .3. 5 / 2 .3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){ 5 / 2 }
116	Gran icosidodecaedro romo		Gran hexecontaedro pentagonal		|2 5 / 2 5 / 2	3.3.3.3.5 / 2​	I	U57	K62	60	150	92	(20+60){3}+12{ 5 / 2 }
117	Gran icosidodecaedro retrosnub		Gran hexecontaedro pentagrammico		| 3 / 2 5 / 3 2	(3.3.3.3.5 / 2 ) / 2	I	U74	K79	60	150	92	(20+60){3}+12{ 5 / 2 }
118	Icosicosidodecaedro retrorromo pequeño		Hexecontaedro hexagramático pequeño		| 3 / 2 3 / 2 5 / 2	( 3.3.3.3.3.5 / 2 )/ 2	Yo soy	U72	K77	180	60	112	(40+60){3}+12{ 5 / 2 }
119	Gran dirrombicosidodecaedro		Gran dirrómbicosidodecacrón		| 3 / 2 5 / 3 3 5 / 2	(4. 5 / 3 .4.3.4. 5 / 2 .4. 3 / 2 )/ 2	Yo soy	U75	K80	60	240	124	40{3}+60{4}+24{ 5 / 2 }

• Lista de poliedros uniformes
• Los cincuenta y nueve icosaedros
• Lista de estelaciones poliédricas

• Wenninger, Magnus (1974). Modelos de poliedros . Cambridge University Press. ISBN 0-521-09859-9.
  • Errata
    • En Wenninger, la figura del vértice para W90 se muestra incorrectamente como si tuviera bordes paralelos.
• Wenninger, Magnus (1979). Modelos esféricos . Cambridge University Press. ISBN 0-521-29432-0.

• Magnus J. Wenninger
• Software utilizado para generar imágenes en este artículo:
  • Stella: Polyhedron Navigator Stella (software) : puede crear e imprimir redes para todos los modelos de poliedros de Wenninger.
  • Subprograma de estelaciones de poliedros de Vladimir Bulatov
  • El subprograma Polyhedra Stellations de Vladimir Bulatov empaquetado como una aplicación para OS X Archivado el 4 de marzo de 2016 en Wayback Machine
• M. Wenninger, Modelos de poliedros, Erratas: errores conocidos en las distintas ediciones.