3 21 politopo

3 21		2 31		1 32
Rectificado 3 21			birectificado 3 21
Rectificado 2 31			Rectificado 1 32
Proyecciones ortogonales en el plano E 7 de Coxeter

En geometría de 7 dimensiones , el politopo 3 ₂₁ es un 7-politopo uniforme , construido dentro de la simetría del grupo E _7. Fue descubierto por Thorold Gosset , publicado en su artículo de 1900. Lo llamó una figura semirregular 7-ica . ^[1]

Su símbolo de Coxeter es 3 ₂₁ , que describe su diagrama bifurcado de Coxeter-Dynkin , con un solo anillo en el extremo de una de las secuencias de 3 nodos.

El 3 ₂₁ rectificado se construye con puntos en los bordes medios del 3 ₂₁ . El 3 ₂₁ birectificado se construye con puntos en los centros de las caras triangulares del 3 ₂₁ . El 3 ₂₁ trirectificado se construye con puntos en los centros tetraédricos del 3 ₂₁ , y es el mismo que el 1 ₃₂ rectificado .

Estos politopos son parte de una familia de 127 (2 ⁷ -1) politopos uniformes convexos en 7 dimensiones , compuestos por facetas de 6 politopos uniformes y figuras de vértice , definidos por todas las permutaciones de anillos en este diagrama de Coxeter-Dynkin :.

3 21 politopo
Tipo	Politopo 7 uniforme
Familia	k 21 politopo
Símbolo de Schläfli	{3,3,3,3 2,1 }
Símbolo de Coxeter	3 21
Diagrama de Coxeter
6 caras	702 en total: 126 3 11 576 {3 5 }
5 caras	6048: 4032 {3 4 } 2016 {3 4 }
4 caras	12096 {3 3 }
Células	10080 {3,3}
Caras	4032 {3}
Bordes	756
Vértices	56
Figura de vértice	2 21 politopo
Polígono de Petrie	octadecágono
Grupo Coxeter	E 7 , [3 3,2,1 ], orden 2903040
Propiedades	convexo

En geometría de siete dimensiones , el politopo 3 ₂₁ es un politopo uniforme . Tiene 56 vértices y 702 facetas: 126 3 ₁₁ y 576 6-símplex .

Para su visualización, este politopo de siete dimensiones suele mostrarse en una dirección de proyección ortográfica sesgada especial que encaja sus 56 vértices dentro de un polígono regular de 18 gonales (llamado polígono de Petrie ). Sus 756 aristas se dibujan entre 3 anillos de 18 vértices y 2 vértices en el centro. También se pueden extraer y dibujar elementos superiores específicos (caras, celdas, etc.) en esta proyección.

El esqueleto 1 del politopo 3 ₂₁ es el gráfico de Gosset .

Este politopo, junto con el 7-símplex , puede teselar el espacio de 7 dimensiones, representado por 3 ₃₁ y el diagrama de Coxeter-Dynkin:.

• También se le llama politopo de Hess en honor a Edmund Hess, quien lo descubrió por primera vez.
• Fue enumerado por Thorold Gosset en su artículo de 1900. Lo llamó figura semirregular 7-ic . ^[1]
• EL Elte lo denominó V ₅₆ (por sus 56 vértices) en su lista de politopos semirregulares de 1912. ^[2]
• HSM Coxeter lo denominó 3 ₂₁ debido a su diagrama bifurcado de Coxeter-Dynkin , que tiene 3 ramas de longitud 3, 2 y 1, y tiene un solo anillo en el nodo final de la rama 3.
• Hecatonicosihexa-pentacosiheptacontihexa-exón (acrónimo Naq) - poliexón facetado 126-576 (Jonathan Bowers) ^[3]

Los 56 vértices se pueden representar de forma más sencilla en un espacio de 8 dimensiones, obtenido mediante las 28 permutaciones de las coordenadas y su opuesto:

± (-3, -3, 1, 1, 1, 1, 1, 1)

Su construcción se basa en el grupo E7 . Coxeter lo denominó como 3 ₂₁ por su diagrama de Coxeter-Dynkin bifurcado , con un solo anillo al final de la secuencia de 3 nodos.

La información de la faceta se puede extraer de su diagrama de Coxeter-Dynkin ,.

Al eliminar el nodo de la rama corta queda el 6-símplex ..

Al eliminar el nodo en el extremo de la rama de 2 longitudes, queda el ortoplex 6 en su forma alternada: 3 ₁₁ ,.

Cada faceta simplex toca una faceta 6-ortoplex, mientras que facetas alternas del ortoplex tocan un simplex u otro ortoplex.

La figura del vértice se determina eliminando el nodo anillado y anillando el nodo vecino. Esto forma un politopo 2 _{21 .}.

Visto en una matriz de configuración , los recuentos de elementos se pueden derivar mediante la eliminación del espejo y las proporciones de los órdenes del grupo de Coxeter . ^[4]

E7​		k -cara	por favor	o0​	el 1	el 2	F3​	F4​	5​		6​		k -cifras	notas
E6​		( )	o0​	56	27	216	720	1080	432	216	72	27	2 21	E7 /E6 = 72x8!/72x6! = 56
D5A1​​​		{ }	el 1	2	756	16	80	160	80	40	16	10	5-demicubes	E7 / D5A1 = 72x8 !/16/5!/2 = 756
Un 4 Un 2		{3}	el 2	3	3	4032	10	30	20	10	5	5	5 celdas rectificadas	E 7 /A 4 A 2 = 72x8!/5!/2 = 4032
Un 3 Un 2 Un 1		{3,3}	F3​	4	6	4	10080	6	6	3	2	3	prisma triangular	E7 / A3A2A1 = 72x8 !/ 4 !/3!/ 2 = 10080
Un 4 Un 1		{3,3,3}	F4​	5	10	10	5	12096	2	1	1	2	triángulo isósceles	E 7 /A 4 A 1 = 72x8!/5!/2 = 12096
Un 5 Un 1		{3,3,3,3}	5​	6	15	20	15	6	4032	*	1	1	{ }	E 7 /A 5 A 1 = 72x8!/6!/2 = 4032
Un 5				6	15	20	15	6	*	2016	0	2		E7 /A5 = 72x8! / 6! = 2016
Un 6		{3,3,3,3,3}	6​	7	21	35	35	21	10	0	576	*	( )	E7 /A6 = 72x8!/ 7 ! = 576
D6​		{3,3,3,3,4}		12	60	160	240	192	32	32	*	126		E7 / D6 = 72x8!/32/6! = 126

Proyecciones del plano de Coxeter

E7	E6 / F4	B7 / A6
[18]	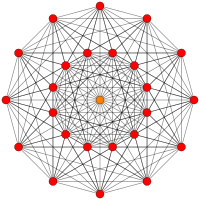[12]	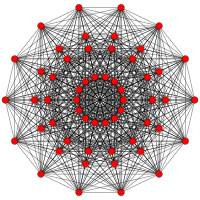[7x2]
A5	D7 / B6	D6 / B5
[6]	[12/2]	[10]
D5 / B4 / A4	D4 / B3 / A2 / G2	D3 / B2 / A3
[8]	[6]	[4]

El 3 ₂₁ es el quinto de una serie dimensional de politopos semirregulares . Cada politopo uniforme progresivo es una figura de vértice construida del politopo anterior. Thorold Gosset identificó esta serie en 1900 como la que contiene todas las facetas de politopos regulares , que contienen todos los símplex y ortoplexes .

k 21 figuras en n dimensiones
Espacio	Finito						Euclidiano	Hiperbólico
En​	3	4	5	6	7	8	9	10
Grupo Coxeter	E3 = Un2Un1​​​	E4 = A4​	E5 = D5​	E6​	E7​	E8​	E9 = = E8 +​${\displaystyle {\tilde {E}}_{8}}$	E10 = = E8 ++​${\displaystyle {\bar {T}}_{8}}$
Diagrama de Coxeter
Simetría	[3 −1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[3 2,2,1 ]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Orden	12	120	1.920	51.840	2.903.040	696.729.600	∞
Gráfico							-	-
Nombre	-1 21	0 21	1 21	2 21	321	4 21	5 21	6 21

Se trata de una serie dimensional de politopos y panales uniformes, expresada por Coxeter como una serie 3 _k1 . (Existe un caso degenerado de 4 dimensiones como teselación de 3 esferas, un hosoedro tetraédrico ).

Figuras tridimensionales de 3 _k1

Espacio	Finito				Euclidiano	Hiperbólico
norte	4	5	6	7	8	9
Grupo Coxeter	Un 3 Un 1	Un 5	D6​	E7​	${\displaystyle {\tilde {E}}_{7}}$=E 7 +	${\displaystyle {\bar {T}}_{8}}$= E7 ++
Diagrama de Coxeter
Simetría	[3 −1,3,1 ]	[3 0,3,1 ]	[[3 1,3,1 ]] = [4,3,3,3,3]	[3 2,3,1 ]	[3 3,3,1 ]	[3 4,3,1 ]
Orden	48	720	46.080	2.903.040	∞
Gráfico					-	-
Nombre	3 1,-1	3 10	3 11	321	3 31	341

Politopo rectificado 3 21
Tipo	Politopo 7 uniforme
Símbolo de Schläfli	t1 { 3,3,3,3 2,1 }
Símbolo de Coxeter	1 ( 3 21 )
Diagrama de Coxeter
6 caras	758
5 caras	44352
4 caras	70560
Células	48384
Caras	11592
Bordes	12096
Vértices	756
Figura de vértice	Prisma de 5 demicubes
Polígono de Petrie	octadecágono
Grupo Coxeter	E 7 , [3 3,2,1 ], orden 2903040
Propiedades	convexo

• Hecatonicosihexa-pentacosiheptacontihexa-exón rectificado como un poliexón facetado 126-576 rectificado (acrónimo ranq) (Jonathan Bowers) ^[5]

Su construcción se basa en el grupo E7 . Coxeter lo denominó como 3 ₂₁ por su diagrama de Coxeter-Dynkin bifurcado , con un solo nodo al final de la secuencia de 3 nodos.

La información de la faceta se puede extraer de su diagrama de Coxeter-Dynkin ,.

Al eliminar el nodo de la rama corta queda el 6-símplex ..

Al eliminar el nodo en el extremo de la rama de 2 longitudes, queda el ortoplex 6 rectificado en su forma alternada: t ₁ 3 ₁₁ ,.

Al quitar el nodo en el extremo de la rama de 3 longitudes, queda el 2 ₂₁ ,.

La figura del vértice se determina eliminando el nodo anillado y anillando el nodo vecino. Esto forma un prisma de 5 demicubes ..

Proyecciones del plano de Coxeter

E7	E6 / F4	B7 / A6
[18]	[12]	[7x2]
A5	D7 / B6	D6 / B5
[6]	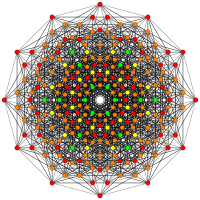[12/2]	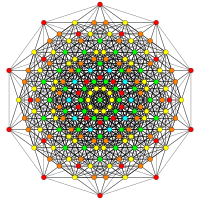[10]
D5 / B4 / A4	D4 / B3 / A2 / G2	D3 / B2 / A3
[8]	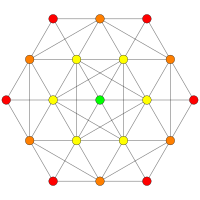[6]	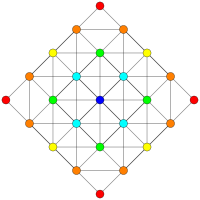[4]

Politopo birectificado 3 21
Tipo	Politopo 7 uniforme
Símbolo de Schläfli	t2 { 3,3,3,3 2,1 }
Símbolo de Coxeter	dos ( 3 21 )
Diagrama de Coxeter
6 caras	758
5 caras	12348
4 caras	68040
Células	161280
Caras	161280
Bordes	60480
Vértices	4032
Figura de vértice	Duoprisma triangular de 5 celdas
Polígono de Petrie	octadecágono
Grupo Coxeter	E 7 , [3 3,2,1 ], orden 2903040
Propiedades	convexo

• Hecatonicosihexa-pentacosiheptacontihexa-exón birectificado como un poliexón facetado birectificado 126-576 (acrónimo branq) (Jonathan Bowers) ^[6]

Su construcción se basa en el grupo E7 . Coxeter lo denominó como 3 ₂₁ por su diagrama de Coxeter-Dynkin bifurcado , con un solo nodo al final de la secuencia de 3 nodos.

La información de la faceta se puede extraer de su diagrama de Coxeter-Dynkin ,.

Al eliminar el nodo de la rama corta queda el 6-símplex birectificado ..

Al eliminar el nodo en el extremo de la rama de 2 longitudes, queda el 6-ortoplex birectificado en su forma alternada: t ₂ (3 ₁₁ ) ,.

Al eliminar el nodo en el extremo de la rama de 3 longitudes, queda el politopo rectificado 2 ₂₁ en su forma alternada: t ₁ (2 ₂₁ ) ,.

La figura del vértice se determina eliminando el nodo anillado y anillando el nodo vecino. Esto produce un duoprisma de triángulo de 5 celdas rectificado ..

Proyecciones del plano de Coxeter

E7	E6 / F4	B7 / A6
[18]	[12]	[7x2]
A5	D7 / B6	D6 / B5
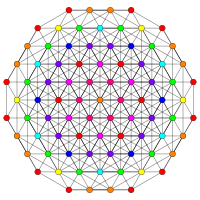[6]	[12/2]	[10]
D5 / B4 / A4	D4 / B3 / A2 / G2	D3 / B2 / A3
[8]	[6]	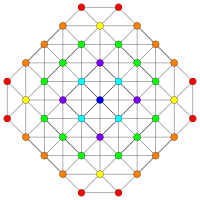[4]

• Lista de politopos E7

• T. Gosset : Sobre las figuras regulares y semirregulares en el espacio de n dimensiones , Messenger of Mathematics, Macmillan, 1900
• Elte, EL (1912), Los politopos semirregulares de los hiperespacios , Groningen: Universidad de Groningen
• HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
• Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
  • (Artículo 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45] Véase p342 (figura 3.7c) de Peter mcMullen: (gráfico de nodos y aristas de 18 gonales de 3 ₂₁ )
• Klitzing, Richard. "Polytopos uniformes 7D (poliexa)".o3o3o3o *c3o3o3x - naq, o3o3o3o *c3o3x3o - ranq, o3o3o3o *c3x3o3o - branq

• Los politopos de Gosset en vZome