Poliedro estrellado uniforme

En geometría , un poliedro uniforme en estrella es un poliedro uniforme que se autointersecta . A veces también se los llama poliedros no convexos para implicar que se autointersectan. Cada poliedro puede contener caras de polígonos en estrella , figuras de vértices de polígonos en estrella o ambas.

El conjunto completo de 57 poliedros estelares uniformes no prismáticos incluye los 4 regulares, llamados poliedros de Kepler-Poinsot , 14 cuasirregulares y 39 semirregulares.

También hay dos conjuntos infinitos de prismas estelares uniformes y antiprismas estelares uniformes .

Así como los polígonos estrella (no degenerados) (cuya densidad de polígonos es mayor que 1) corresponden a polígonos circulares con teselas superpuestas , los poliedros estrella que no pasan por el centro tienen una densidad de politopos mayor que 1, y corresponden a poliedros esféricos con teselas superpuestas; existen 47 poliedros estrella uniformes no prismáticos de este tipo. Los 10 poliedros estrella uniformes no prismáticos restantes, aquellos que pasan por el centro, son los hemipoliedros así como el monstruo de Miller , y no tienen densidades bien definidas.

Las formas no convexas se construyen a partir de triángulos de Schwarz .

A continuación se enumeran todos los poliedros uniformes ordenados por sus grupos de simetría y subagrupados según sus disposiciones de vértices.

Los poliedros regulares se identifican con su símbolo de Schläfli . Otros poliedros uniformes no regulares se indican con su configuración de vértices .

Una figura adicional, el pseudo gran rombicuboctaedro , no suele incluirse como un politopo estelar verdaderamente uniforme, a pesar de constar de caras regulares y tener los mismos vértices.

Nota: Para las formas no convexas que se muestran a continuación, se utiliza un descriptor adicional , no uniforme, cuando la disposición de los vértices de la envoltura convexa tiene la misma topología que una de estas, pero tiene caras no regulares. Por ejemplo, una forma cantelada no uniforme puede tener rectángulos creados en lugar de los bordes en lugar de cuadrados .

Ver Poliedro prismático uniforme .

Existe una forma no convexa, el tetrahemihexaedro , que tiene simetría tetraédrica (con dominio fundamental: triángulo de Möbius (3 3 2)).

Existen dos triángulos de Schwarz que generan poliedros uniformes no convexos únicos: un triángulo rectángulo ( 3 ⁄ 2 3 2 ), y un triángulo general ( 3 ⁄ 2 3 3 ). El triángulo general ( 3 ⁄ 2 3 3 ) genera el octahemioctaedro que se da más adelante con su simetría octaédrica completa .

Disposición de vértices ( envolvente convexa )	Formas no convexas
Tetraedro
Tetraedro rectificado Octaedro	4. 3 ⁄ 2 .4.3 3 ⁄ 2 3 | 2
Tetraedro truncado
Tetraedro cantelado ( Cuboctaedro )
Tetraedro omnitruncado ( Octaedro truncado )
Tetraedro romo ( icosaedro )

Hay 8 formas convexas y 10 formas no convexas con simetría octaédrica (con dominio fundamental triángulo de Möbius (4 3 2)).

Hay cuatro triángulos de Schwarz que generan formas no convexas, dos triángulos rectángulos ( 3 ⁄ 2 4 2) y ( 4 ⁄ 3 3 2), y dos triángulos generales: ( 4 ⁄ 3 4 3), ( 3 ⁄ 2 4 4).

Disposición de vértices ( envolvente convexa )	Formas no convexas
Cubo
Octaedro
Cuboctaedro	6. 4 ⁄ 3 .6.4 4 ⁄ 3 4 | 3	6. 3 ⁄ 2 .6.3 3 ⁄ 2 3 | 3
Cubo truncado	4. 8 ⁄ 3 . 4 ⁄ 3 . 8 ⁄ 5 2 4 ⁄ 3 ( 3 ⁄ 2 4 ⁄ 2 ) |	8 ⁄ 3 .3. 8 ⁄ 3 .4 3 4 | 4 ⁄ 3	4. 3 ⁄ 2 .4.4 3 ⁄ 2 4 | 2
Octaedro truncado
Rombicuboctaedro	4.8. 4 ⁄ 3 . 8 ⁄ 7 2 4 ( 3 ⁄ 2 4 ⁄ 2 ) |	8. 3 ⁄ 2 .8.4 3 ⁄ 2 4 | 4	8 ⁄ 3 . 8 ⁄ 3 .3 2 3 | 4 ⁄ 3
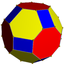Cuboctaedro truncado no uniforme	4.6.8 ⁄ 3 2 3 4 ⁄ 3 |
Cuboctaedro truncado no uniforme	8 ⁄ 3 .6.8 3 4 4 ⁄ 3 |
Cubo de snub

Hay 8 formas convexas y 46 formas no convexas con simetría icosaédrica (con triángulo de Möbius de dominio fundamental (5 3 2)). (o 47 formas no convexas si se incluye la figura de Skilling). Algunas de las formas no convexas de snub tienen simetría de vértice reflexiva.

Disposición de vértices ( envolvente convexa )	Formas no convexas
Icosaedro	{5, 5 ⁄ 2 }	{ 5 ⁄ 2 ,5}	{3, 5 ⁄ 2 }
Icosaedro truncado no uniforme	10.10. 5 ⁄ 2 2 5 ⁄ 2 | 5	3. 10 ⁄ 3 . 5 ⁄ 2 . 10 ⁄ 7 5 ⁄ 2 3 | 5 ⁄ 3	3.4.5 ⁄ 3 .4 5 ⁄ 3 3 | 2	4. 10 ⁄ 3 . 4 ⁄ 3 . 10 ⁄ 7 2 5 ⁄ 3 ( 3 ⁄ 2 5 ⁄ 4 ) |
Icosaedro truncado no uniforme	4. 5 ⁄ 2 .4.5 5 ⁄ 2 5 | 2	5.6.5 ⁄ 3 .6 5 ⁄ 3 5 | 3	4.6. 4 ⁄ 3 . 6 ⁄ 5 2 3 ( 5 ⁄ 4 5 ⁄ 2 ) |
Icosaedro truncado no uniforme	3 5 . 5 ⁄ 2 | 5 ⁄ 2 3 3
Icosidodecaedro	3.10. 3 ⁄ 2 .10 3 ⁄ 2 3 | 5	5.10. 5 ⁄ 4 .10 5 ⁄ 4 5 | 5	3. 5 ⁄ 2 .3. 5 ⁄ 2 2 | 3 5 ⁄ 2	5 ⁄ 2 . 10 ⁄ 3 . 5 ⁄ 3 . 10 ⁄ 3 5 ⁄ 3 5 ⁄ 2 | 5 ⁄ 3	3. 10 ⁄ 3 . 3 ⁄ 2 . 10 ⁄ 3 3 3 | 5 ⁄ 3	5. 5 ⁄ 2 .5. 5 ⁄ 2 2 | 5 5 ⁄ 2	6. 5 ⁄ 2 .6. 5 ⁄ 3 5 ⁄ 3 5 ⁄ 2 | 3	5.6.5 ⁄ 4 .6 5 ⁄ 4 5 | 3
dodecaedro truncado	3. 10 ⁄ 3 .5. 10 ⁄ 3 3 5 | 5 ⁄ 3	5.6.3 ⁄2 .63 ⁄2 5 | 3​​	6. 10 ⁄ 3 . 6 ⁄ 5 . 10 ⁄ 7 3 5 ⁄ 3 ( 3 ⁄ 2 5 ⁄ 2 ) |
Dodecaedro truncado no uniforme	(3 5 . 5 ⁄ 3 )/2 | 3 ⁄ 2 3 ⁄ 2 5 ⁄ 2
Dodecaedro	{ 5 ⁄ 2 ,3}	(3,5 ⁄ 2 ) 3 3 | 5 ⁄ 2 3	( 5,5⁄3 ) 33 | 5⁄35​​​​​	((3,5) 3 )/2 3 ⁄ 2 | 3 5
rombicosidodecaedro	5.10. 3 ⁄ 2 .10 3 ⁄ 2 5 | 5	4.10. 4 ⁄ 3 . 10 ⁄ 9 2 5 ( 3 ⁄ 2 5 ⁄ 2 ) |	5. 10 ⁄ 3 . 10 ⁄ 3 2 5 | 5 ⁄ 3
Rombicosidodecaedro no uniforme	6.6.5 ⁄ 2 2 5 ⁄ 2 | 3
Rombicosidodecaedro no uniforme	6. 5 ⁄ 2 .6.3 5 ⁄ 2 3 | 3	3.10. 5 ⁄ 3 .10 5 ⁄ 3 3 | 5	6.10. 6 ⁄ 5 . 10 ⁄ 9 3 5 ( 3 ⁄ 2 5 ⁄ 4 ) |	3. 10 ⁄ 3 . 10 ⁄ 3 2 3 | 5 ⁄ 3
Rombicosidodecaedro no uniforme	4. 5 ⁄ 3 .4.3.4. 5 ⁄ 2 .4. 3 ⁄ 2 | 3 ⁄ 2 5 ⁄ 3 3 5 ⁄ 2	3.3.3. 5 ⁄ 2 .3. 5 ⁄ 3 | 5 ⁄ 3 5 ⁄ 2 3	Figura de Skilling (ver abajo)
Icosidodecaedro truncado no uniforme	6.10.10 ⁄ 3 3 5 5 ⁄ 3 |
Icosidodecaedro truncado no uniforme	4. 10 ⁄ 9 . 10 ⁄ 3 2 5 5 ⁄ 3 |
Icosidodecaedro truncado no uniforme	4.6.10 ⁄ 3 2 3 5 ⁄ 3 |
Dodecaedro romo no uniforme	3.3. 5 ⁄ 2 .3.5 | 2 5 ⁄ 2 5	3.3.3.5.3. 5 ⁄ 3 | 5 ⁄ 3 3 5	3 4 . 5 ⁄ 2 | 2 5 ⁄ 2 3	3 4 . 5 ⁄ 3 | 5 ⁄ 3 2 3	3.3.5.3. 5 ⁄ 3 | 5 ⁄ 3 2 5	(3 4 . 5 ⁄ 2 )/2 | 3 ⁄ 2 5 ⁄ 3 2

Coxeter identificó una serie de poliedros estelares degenerados mediante el método de construcción de Wythoff, que contienen aristas o vértices superpuestos. Estas formas degeneradas incluyen:

• Icosidodecaedro complejo pequeño
• Gran icosidodecaedro complejo
• Pequeño rombicosidodecaedro complejo
• Gran rombicosidodecaedro complejo
• Rombidodecadodecaedro complejo

Otro poliedro degenerado no convexo es el gran dirrombidodecaedro desprovisto de protuberancias , también conocido como figura de Skilling , que es uniforme en sus vértices, pero tiene pares de aristas que coinciden en el espacio de modo que cuatro caras se encuentran en algunas aristas. Se considera un poliedro uniforme degenerado en lugar de un poliedro uniforme debido a sus aristas dobles. Tiene simetría I _{h .}

• Polígono estrellado
• Lista de poliedros uniformes
• Lista de poliedros uniformes según el triángulo de Schwarz

• Coxeter, HSM (13 de mayo de 1954). "Poliedros uniformes". Philosophical Transactions of the Royal Society of London. Serie A, Ciencias matemáticas y físicas . 246 (916): 401–450. doi :10.1098/rsta.1954.0003.
• Wenninger, Magnus (1974). Modelos de poliedros . Cambridge University Press. ISBN 0-521-09859-9.OCLC 1738087  .
• Brückner, M. Vielecke und vielflache. Theorie und geschichte. . Leipzig, Alemania: Teubner, 1900. [1]
• Sopov, SP (1970), "Una prueba de la completitud de la lista de poliedros homogéneos elementales", Ukrainskiui Geometricheskiui Sbornik (8): 139–156, MR  0326550
• Skilling, J. (1975), "El conjunto completo de poliedros uniformes", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences , 278 : 111–135, doi :10.1098/rsta.1975.0022, ISSN  0080-4614, JSTOR  74475, MR  0365333
• Har'El, Z. Solución uniforme para polihedras uniformes., Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El, software Kaleido, Imágenes, imágenes duales
• Mäder, RE Poliedros uniformes. Mathematica J. 3, 48-57, 1993. [2]
• Messer, Peter W. Expresiones de forma cerrada para poliedros uniformes y sus duales., Geometría discreta y computacional 27:353-375 (2002).
• Klitzing, Richard. "Poliedros uniformes 3D".

• Weisstein, Eric W. "Poliedro uniforme". MathWorld .