Poliedro pseudouniforme

Un poliedro pseudouniforme es un poliedro que tiene polígonos regulares como caras y tiene la misma configuración de vértices en todos los vértices , pero no es transitivo en relación con los vértices : no es cierto que para dos vértices cualesquiera, exista una simetría del poliedro que aplique el primero isométricamente al segundo. Por lo tanto, aunque todos los vértices de un poliedro pseudouniforme parezcan iguales, no es isogonal . Se denominan poliedros pseudouniformes debido a su semejanza con algunos poliedros uniformes verdaderos .

Se conocen dos poliedros pseudouniformes: el pseudorrombicuboctaedro y el pseudorrombicuboctaedro grande . No se sabe si existen otros; Branko Grünbaum conjeturó que no los hay, pero pensó que una demostración sería "probablemente bastante complicada". ^[1] Ambos tienen simetría D _4d , la misma simetría que un antiprisma cuadrado . Ambos pueden construirse a partir de un poliedro uniforme girando una tapa en forma de cúpula .

Los poliedros pseudouniformes

Pseudorrombicuboctaedro

El pseudorhombicuboctaedro es el único poliedro pseudouniforme convexo. También es un sólido de Johnson (J ₃₇ ) y también puede llamarse girobicúpula cuadrada alargada . Su dual es el icositetraedro pseudodeltoidal. Como sugiere el nombre, puede construirse alargando una girobicúpula cuadrada ( J ₂₉ ) e insertando un prisma octogonal entre sus dos mitades. El sólido resultante es localmente regular en sus vértices: la disposición de las cuatro caras incidentes en cualquier vértice es la misma para todos los vértices; esto es único entre los sólidos de Johnson. Sin embargo, no es transitivo en sus vértices y, en consecuencia, no es uno de los sólidos de Arquímedes , ya que hay pares de vértices tales que no hay isometría del sólido que mapee uno en el otro. Esencialmente, los dos tipos de vértices pueden distinguirse por sus "vecinos de vecinos". Otra forma de ver que el poliedro no es regular en sus vértices es observar que hay exactamente un cinturón de ocho cuadrados alrededor de su ecuador, que distingue los vértices del cinturón de los vértices de cada lado.

Rombicuboctaedro	Secciones despiezadas	Pseudo-rombicuboctaedro

El sólido también puede verse como el resultado de torcer una de las cúpulas cuadradas ( J ₄ ) en un rombicuboctaedro (uno de los sólidos de Arquímedes ; también conocido como ortobicúpula cuadrada alargada) en 45 grados. Su similitud con el rombicuboctaedro le da el nombre alternativo de pseudorrombicuboctaedro . En ocasiones se lo ha denominado "el decimocuarto sólido de Arquímedes".

Con caras coloreadas por su simetría D _4d , puede verse así:

pseudorrombicuboctaedro		Icositetraedro pseudodeltoidal Poliedro dual
neto

Hay 8 cuadrados (verdes) alrededor de su ecuador , 4 triángulos (rojos) y 4 cuadrados (amarillos) arriba y abajo, y un cuadrado (azul) en cada polo.

La construcción de los rombicuboctaedros uniformes y pseudorrobicos se puede observar en las siguientes ampliaciones del prisma octogonal:

El prisma octogonal (coloreado con simetría D _8h )...	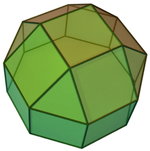...con uno de los octógonos aumentado con una cúpula cuadrada.	Existen dos opciones para la orientación de la otra cúpula cuadrada no cruzada. Una alinea las caras correspondientes (triángulos con triángulos, cuadrados con cuadrados) y produce el rombicuboctaedro. Esta construcción tiene simetría D _4h , aunque el rombicuboctaedro tiene simetría octaédrica completa.	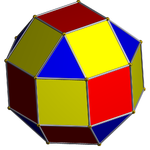La otra opción alinea las caras no correspondientes (triángulos con cuadrados) y produce el pseudorrombicuboctaedro . Esta construcción tiene simetría D _{4d .}

Pseudo-gran rombicuboctaedro

El gran rombicuboctaedro uniforme no convexo puede verse como un prisma octagrámico con los octagramas excavados con cúpulas cuadradas cruzadas, de manera similar a cómo el rombicuboctaedro puede verse como un prisma octagonal con los octógonos aumentados con cúpulas cuadradas. Al rotar una de las cúpulas en esta construcción se obtiene el pseudogran rombicuboctaedro .

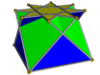Cúpula cuadrada cruzada	Gran rombicuboctaedro no convexo	Pseudo-gran rombicuboctaedro

Las imágenes que aparecen a continuación muestran la excavación del prisma octagrámico con cúpulas cuadradas cruzadas, que se lleva a cabo paso a paso. Las cúpulas cuadradas cruzadas siempre son de color rojo, mientras que los lados cuadrados del prisma octagrámico están en los otros colores. Todas las imágenes están orientadas aproximadamente de la misma manera para mayor claridad.

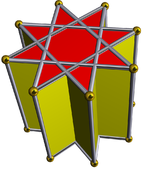El prisma octagrámico (coloreado con simetría D _8h )...	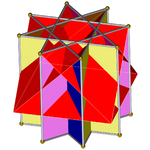... con uno de los octagramas (aquí, el de arriba) excavado con una cúpula cuadrada cruzada. Esta puede denominarse cúpula cuadrada cruzada retroelongada o prisma octagrámico aumentado , y es isomorfa a la cúpula cuadrada alargada de Johnson .	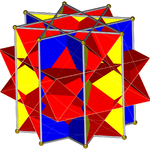Hay dos opciones para la orientación de la otra cúpula cuadrada cruzada. Una alinea las caras correspondientes (triángulos con triángulos, cuadrados con cuadrados) y produce el gran rombicuboctaedro no convexo. Esta construcción tiene simetría D _{4h , aunque el gran rombicuboctaedro no convexo tiene}simetría octaédrica completa .	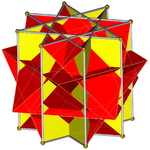La otra opción alinea las caras no correspondientes (triángulos con cuadrados) y produce el pseudo-gran rombicuboctaedro (o pseudocuasirombicuboctaedro). Esta construcción tiene simetría D _4d .

El pseudo gran rombicuboctaedro tiene un único "cinturón" de cuadrados alrededor de su ecuador y se puede construir girando 45 grados una de las cúpulas cuadradas cruzadas de un gran rombicuboctaedro no convexo. Esto es análogo al pseudorrombicuboctaedro.

Duales de los poliedros pseudouniformes

Los duales de los poliedros pseudouniformes tienen todas sus caras congruentes , pero no transitivas: sus caras no se encuentran todas dentro de la misma órbita de simetría y, por lo tanto, no son isoédricos . Esto es una consecuencia de que los poliedros pseudouniformes tienen la misma configuración de vértices en cada vértice, pero no son transitivos en sus vértices . Esto se demuestra por los diferentes colores utilizados para las caras en las imágenes de los poliedros pseudouniformes duales en este artículo, que denotan diferentes tipos de caras.

Icositetraedro pseudodeltoidal

Icositetraedro deltoidal pseudo-grande

Referencias

^ Grünbaum, Branko (2009), "Un error duradero" (PDF) , Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR 2520469. Reimpreso en Pitici, Mircea, ed. (2011). Los mejores escritos sobre matemáticas 2010. Princeton University Press. págs. 18–31..

[1] Grünbaum, Branko (2009), "Un error duradero" (PDF) , Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR 2520469. Reimpreso en Pitici, Mircea, ed. (2011). Los mejores escritos sobre matemáticas 2010. Princeton University Press. págs. 18–31..