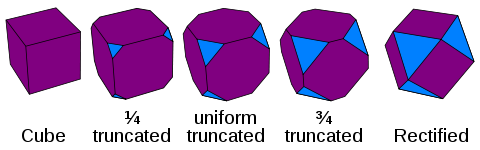
Politopo uniforme
| 2D | 3D |
|---|---|
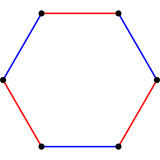 Triángulo truncado o hexágono uniforme , con diagrama de Coxeter    . . | 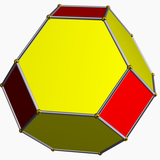 Octaedro truncado ,      |
| 4D | 5D |
 16 celdas truncadas        |  5-ortoplex truncado ,          |
En geometría , un politopo uniforme de dimensión tres o superior es un politopo transitivo por vértices limitado por facetas uniformes . Aquí, "transitivo por vértices" significa que tiene simetrías que llevan cada vértice a cada uno de los otros vértices; lo mismo debe ser cierto también dentro de cada cara de dimensión inferior del politopo. En dos dimensiones (y para las caras bidimensionales de politopos de dimensión superior) se utiliza una definición más fuerte: solo los polígonos regulares se consideran uniformes, lo que no permite polígonos que alternan entre dos longitudes diferentes de aristas.
Esta es una generalización de la categoría anterior de politopos semirregulares , pero también incluye los politopos regulares . Además, se permiten caras regulares en forma de estrella y figuras de vértice ( polígonos en forma de estrella ), lo que amplía enormemente las posibles soluciones. Una definición estricta requiere que los politopos uniformes sean finitos, mientras que una definición más expansiva permite que los panales uniformes ( teselados bidimensionales y panales de dimensiones superiores ) del espacio euclidiano e hiperbólico también se consideren politopos.
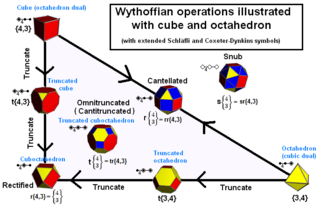
Operaciones
Casi todos los politopos uniformes pueden generarse mediante una construcción de Wythoff y representarse mediante un diagrama de Coxeter . Entre las excepciones más notables se incluyen el gran dirrombicosidodecaedro en tres dimensiones y el gran antiprisma en cuatro dimensiones.
De manera equivalente, los politopos wythoffianos se pueden generar aplicando operaciones básicas a los politopos regulares en esa dimensión. Este enfoque fue utilizado por primera vez por Johannes Kepler y es la base de la notación de poliedros de Conway .
Operadores de rectificación
Los n-politopos regulares tienen n órdenes de rectificación . La rectificación cero es la forma original. La rectificación ( n −1)-ésima es la dual . Una rectificación reduce aristas a vértices, una birectificación reduce caras a vértices, una trirectificación reduce celdas a vértices, una cuadirectificación reduce 4-caras a vértices, una quintirectificación reduce 5-caras a vértices, y así sucesivamente.
Se puede utilizar un símbolo Schläfli extendido para representar formas rectificadas, con un solo subíndice:
- k -ésima rectificación = t k {p 1 , p 2 , ..., p n-1 } = k r .
Operadores de truncamiento
Operaciones de truncamiento que se pueden aplicar a n -politopos regulares en cualquier combinación. El diagrama de Coxeter resultante tiene dos nodos en anillo y la operación se denomina según la distancia entre ellos. El truncamiento corta vértices, la cantelación corta aristas, la runcinación corta caras y la esterificación corta celdas. Cada operación superior también corta las inferiores, por lo que una cantelación también trunca vértices.
- t 0,1 o t : Truncamiento : se aplica a polígonos y de mayor tamaño. Un truncamiento elimina vértices e inserta una nueva faceta en lugar de cada vértice anterior. Las caras se truncan, duplicando sus aristas. (El término, acuñado por Kepler , proviene del latín truncare , "cortar").
- También existen truncamientos superiores: bitruncación t 1,2 o 2t , tritruncación t 2,3 o 3t , cuadritruncación t 3,4 o 4t , quintitruncación t 4,5 o 5t , etc.
- t 0,2 o rr : cantelación - se aplica a poliedros y superiores. Puede verse como una rectificación de su rectificación . Una cantelación trunca tanto los vértices como las aristas y los reemplaza con nuevas facetas. Las celdas se reemplazan por copias expandidas topológicamente de sí mismas. (El término, acuñado por Johnson, se deriva del verbo cant , como bevel , que significa cortar con una cara inclinada).
- También existen cantelaciones superiores: bicantelación t 1,3 o r2r , tricantelación t 2,4 o r3r , cuadricantelación t 3,5 o r4r , etc.
- t 0,1,2 o tr : cantitruncación : se aplica a poliedros y de mayor tamaño. Puede considerarse como un truncamiento de su rectificación . Una cantitruncación trunca tanto los vértices como las aristas y los reemplaza con nuevas facetas. Las celdas se reemplazan por copias de sí mismas expandidas topológicamente . (El término compuesto combina cantelación y truncamiento)
- También existen cantelaciones superiores: bicantitruncamiento t 1,2,3 o t2r , tricantitruncamiento t 2,3,4 o t3r , cuadricantitruncamiento t 3,4,5 o t4r , etc.
- t 0,3 : Runcinación : se aplica a politopos de 4 elementos uniformes y superiores. La runcinación trunca vértices, aristas y caras, reemplazándolos cada uno por facetas nuevas. Las caras de 4 elementos se reemplazan por copias expandidas topológicamente de sí mismas. (El término, acuñado por Johnson, se deriva del latín runcina ' cepillo de carpintero ').
- Existen también runcinaciones superiores: biruncinación t 1,4 , triruncinación t 2,5 , etc.
- t 0,4 o 2r2r : Esterificación : se aplica a politopos de 5-uniformes y superiores. Puede considerarse como una birectificación de su birectificación. La esterificación trunca vértices, aristas, caras y celdas, y reemplaza cada uno de ellos por nuevas facetas. Las caras de 5-uniformes se reemplazan por copias de sí mismas expandidas topológicamente. (El término, acuñado por Johnson, se deriva del griego stereos, "sólido").
- También existen esterificaciones superiores: bistericación t 1,5 o 2r3r , triestericación t 2,6 o 2r4r , etc.
- t 0,2,4 o 2t2r : esterificación : se aplica a politopos uniformes de 5 y superiores. Puede considerarse como una truncación de su birectificación.
- Existen también esterificaciones superiores: bistericantelación t 1,3,5 o 2t3r , triestericantelación t 2,4,6 o 2t4r , etc.
- t 0,5 : Pentelación : se aplica a politopos de 6 elementos uniformes y superiores. La pentelación trunca vértices, aristas, caras, celdas y caras de 4 elementos, y reemplaza cada uno de ellos por nuevas facetas. Las caras de 6 elementos se reemplazan por copias de sí mismas expandidas topológicamente. (La pentelación se deriva del griego pente, "cinco").
- También existen pentelaciones superiores: bipentelación t 1,6 , tripentelación t 2,7 , etc.
- t 0,6 o 3r3r : hexificación : se aplica a politopos de 7-uniformes y superiores. Puede verse como una trirectificación de su trirectificación. La hexificación trunca vértices, aristas, caras, celdas, 4-caras y 5-caras, reemplazando cada una con nuevas facetas. Las 7-caras se reemplazan por copias expandidas topológicamente de sí mismas. (La hexificación se deriva del griego hex 'seis').
- También existen hexicaciones superiores: bihexicación : t 1,7 o 3r4r , trihexicación : t 2,8 o 3r5r , etc.
- t 0,3,6 o 3t3r : hexiruncinado : se aplica a politopos 7 uniformes y superiores. Puede considerarse como un truncamiento de su trirectificación.
- Existen también hexiruncinaciones superiores: bihexiruncinadas : t 1,4,7 o 3t4r , trihexiruncinadas : t 2,5,8 o 3t5r , etc.
- t 0,7 : Heptelación : se aplica a politopos de 8 uniformes y superiores. La heptelación trunca vértices, aristas, caras, celdas, caras de 4, 5 y 6, y reemplaza cada una de ellas por nuevas facetas. Las caras de 8 se reemplazan por copias de sí mismas expandidas topológicamente. (La heptelación se deriva del griego hepta, "siete").
- También existen heptelaciones superiores: biheptelación t 1,8 , triheptelación t 2,9 , etc.
- t 0,8 o 4r4r : Octelación : se aplica a politopos uniformes de 9 y superiores.
- t 0,9 : Enecación : se aplica a politopos uniformes de 10 y superiores.
Además, se pueden realizar combinaciones de truncamientos que también generen nuevos politopos uniformes. Por ejemplo, un runcitruncamiento es un runcinamiento y un truncamiento aplicados conjuntamente.
Si se aplican todos los truncamientos a la vez, la operación puede denominarse de forma más general " omnitruncamiento" .
Alternancia

Una operación especial, llamada alternancia , elimina vértices alternos de un politopo con solo caras pares. Un politopo omnitruncado alternado se llama snub .
Los politopos resultantes siempre se pueden construir, y generalmente no son reflexivos y, en general, tampoco tienen soluciones de politopos uniformes .
El conjunto de politopos formados al alternar los hipercubos se conoce como demicubos . En tres dimensiones, esto produce un tetraedro ; en cuatro dimensiones, esto produce un tetraedro de 16 celdas o demicubo .
Figura de vértice
Los politopos uniformes se pueden construir a partir de su figura de vértice , la disposición de aristas, caras, celdas, etc. alrededor de cada vértice. Los politopos uniformes representados por un diagrama de Coxeter , que marca los espejos activos mediante anillos, tienen simetría reflexiva y se pueden construir de manera sencilla mediante reflexiones recursivas de la figura de vértice.
Un número menor de politopos uniformes no reflexivos tienen una única figura de vértice pero no se repiten mediante reflexiones simples. La mayoría de ellos se pueden representar con operaciones como la alternancia de otros politopos uniformes.
Las figuras de vértice para diagramas de Coxeter de un solo anillo se pueden construir a partir del diagrama eliminando el nodo en anillo y haciendo anillos con los nodos vecinos. Estas figuras de vértice son, en sí mismas, transitivas respecto de los vértices.
Los politopos multianillos se pueden construir mediante un proceso de construcción ligeramente más complicado y su topología no es la de un politopo uniforme. Por ejemplo, la figura del vértice de un politopo regular truncado (con 2 anillos) es una pirámide. Un politopo omnitruncado (con todos los nodos en anillos) siempre tendrá un símplex irregular como figura del vértice.
Circunradio
Los politopos uniformes tienen longitudes de aristas iguales y todos los vértices están a la misma distancia del centro, llamada circunradio .
Los politopos uniformes cuyo radio circunscrito es igual a la longitud de la arista se pueden utilizar como figuras de vértice para panales uniformes . Por ejemplo, el hexágono regular se divide en 6 triángulos equiláteros y es la figura de vértice para el mosaico triangular regular . También el cuboctaedro se divide en 8 tetraedros regulares y 6 pirámides cuadradas (medio octaedro ), y es la figura de vértice para el panal cúbico alternado .
Politopos uniformes por dimensión
Es útil clasificar los politopos uniformes por dimensión. Esto es equivalente al número de nodos en el diagrama de Coxeter, o al número de hiperplanos en la construcción de Wythoff. Debido a que los politopos ( n +1)-dimensionales son teselas de espacio esférico n -dimensional, las teselas de espacio euclidiano e hiperbólico n -dimensional también se consideran ( n +1)-dimensionales. Por lo tanto, las teselas de espacio bidimensional se agrupan con los sólidos tridimensionales.
Una dimensión
El único politopo unidimensional es el segmento de línea. Corresponde a la familia Coxeter A 1 .
Dos dimensiones
En dos dimensiones, existe una familia infinita de politopos convexos uniformes, los polígonos regulares , siendo el más simple el triángulo equilátero . Los polígonos regulares truncados se convierten en polígonos cuasirregulares geométricos bicolores de dos veces más lados, t{p}={2p}. Los primeros polígonos regulares (y formas cuasirregulares) se muestran a continuación:
| Nombre | Triángulo ( 2-símplex ) | Cuadrado ( 2-ortoplex ) ( 2-cubo ) | Pentágono | Hexágono | Heptágono | Octágono | Eneágono | Decágono | Endecágono |
|---|---|---|---|---|---|---|---|---|---|
| Colapso | {3} | {4} y{2} | {5} | {6} y{3} | {7} | {8} y{4} | {9} | {10} y {5} | {11} |
Diagrama de Coxeter |    |       |    |       |    |       |    |       |    |
| Imagen |  |   |  |   |  |   |  |   |  |
| Nombre | Dodecágono | Tridecágono | Tetradecágono | Pentadecágono | Hexadecágono | Heptadecágono | Octadecágono | Eneadecágono | Icoságono |
| Colapso | {12} y {6} | {13} | {14} y{7} | {15} | {16} y {8} | {17} | {18} y {9} | {19} | {20} y {10} |
Diagrama de Coxeter |       |    |       |    |       |    |       |    |       |
| Imagen |   |  |   |  |   |  |   |  |   |
También existe un conjunto infinito de polígonos estrellados (uno por cada número racional mayor que 2), pero estos no son convexos. El ejemplo más simple es el pentagrama , que corresponde al número racional 5/2. Los polígonos estrellados regulares, {p/q}, pueden truncarse en polígonos estrellados semirregulares, t{p/q}=t{2p/q}, pero se convierten en polígonos doblemente cubiertos si q es par. También se puede realizar un truncamiento con un polígono de orientación inversa t{p/(pq)}={2p/(pq)}, por ejemplo t{5/3}={10/3}.
| Nombre | Pentagrama | Heptagramas | Octagrama | Eneagramas | Decagramo | ... n-agramas | ||
|---|---|---|---|---|---|---|---|---|
| Colapso | {5/2} | {7/2} | {7/3} | {8/3} y{4/3} | {9/2} | {9/4} | {10/3} y {5/3} | { p/q } |
Diagrama de Coxeter |      |      |      |           |      |      |           |      |
| Imagen |  |  |  |   |  |  |   | |
Polígonos regulares, representados por el símbolo de Schläfli {p} para un p-gono. Los polígonos regulares son autoduales, por lo que la rectificación produce el mismo polígono. La operación de truncamiento uniforme duplica los lados a {2p}. La operación de truncamiento, alternando el truncamiento, restaura el polígono original {p}. Por lo tanto, todos los polígonos uniformes también son regulares. Las siguientes operaciones se pueden realizar en polígonos regulares para derivar los polígonos uniformes, que también son polígonos regulares:
| Operación | Símbolos Schläfli ampliados | Resultado regular | Diagrama de Coxeter | Posición | Simetría | ||
|---|---|---|---|---|---|---|---|
| (1) | (0) | ||||||
| Padre | {pags} | t0 { p} | {pags} |    | {} | -- | [p] (orden 2p) |
| Rectificado (doble) | p | t1 { p} | {pags} |    | -- | {} | [p] (orden 2p) |
| Truncado | p{p} | t 0,1 {p} | {2p} |    | {} | {} | [[p]]=[2p] (orden 4p) |
| Medio | el{2p} | {pags} |     | -- | -- | [1 + ,2p]=[p] (orden 2p) | |
| Desaire | esp | {pags} |    | -- | -- | [[p]] + =[p] (orden 2p) | |
Tres dimensiones
En tres dimensiones, la situación se vuelve más interesante. Hay cinco poliedros regulares convexos, conocidos como sólidos platónicos :
| Nombre | Colapso {p,q} | Diagrama     | Imagen (transparente) | Imagen (sólida) | Imagen (esfera) | Caras {p} | Bordes | Vértices {q} | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetraedro ( 3-símplex ) (Pirámide) | {3,3} |      |  |  |  | 4 {3} | 6 | 4 {3} | T.D. | (ser) |
| Cubo ( 3-cubos ) (Hexaedro) | {4,3} |      |  |  |  | 6 {4} | 12 | 8 {3} | Oh | Octaedro |
| Octaedro ( 3-ortoplex ) | {3,4} |      |  |  |  | 8 {3} | 12 | 6 {4} | Oh | Cubo |
| Dodecaedro | {5,3} |      |  |  |  | 12 {5} | 30 | 20 {3}2 | Yo soy | Icosaedro |
| Icosaedro | {3,5} |      |  |  |  | 20 {3} | 30 | 12 {5} | Yo soy | Dodecaedro |
Además de estos, también existen 13 poliedros semirregulares, o sólidos arquimedianos , que pueden obtenerse mediante construcciones de Wythoff , o realizando operaciones como el truncamiento en los sólidos platónicos, como se demuestra en la siguiente tabla:
| Padre | Truncado | Rectificado | Bittruncado (tr. dual) | Birectificado (doble) | Cantelado | Omnitruncado ( Cantitruncado ) | Desaire | |
|---|---|---|---|---|---|---|---|---|
| Tetraédrico 3-3-2 |  {3,3} |  (3.6.6) |  (3.3.3.3) |  (3.6.6) |  {3,3} |  (3.4.3.4) |  (4.6.6) |  (3.3.3.3.3) |
| Octaédrico 4-3-2 |  {4,3} |  (3.8.8) |  (3.4.3.4) |  (4.6.6) |  {3,4} |  (3.4.4.4) |  (4.6.8) |  (3.3.3.3.4) |
| Icosaédrica 5-3-2 |  {5,3} |  (3.10.10) |  (3.5.3.5) |  (5.6.6) |  {3,5} |  (3.4.5.4) |  (4.6.10) |  (3.3.3.3.5) |
También existe el conjunto infinito de prismas , uno por cada polígono regular, y un conjunto correspondiente de antiprismas .
| # | Nombre | Imagen | Embaldosado | Figura de vértice | Diagrama y símbolos de Schläfli |
|---|---|---|---|---|---|
| P2p | Prisma |  |  |  |      tr{2,p} |
| Una p | Antiprisma |  |  |  |      sr{2,p} |
Los poliedros estelares uniformes incluyen otros 4 poliedros estelares regulares, los poliedros de Kepler-Poinsot y 53 poliedros estelares semirregulares. También existen dos conjuntos infinitos, los prismas estelares (uno por cada polígono estelar) y los antiprismas estelares (uno por cada número racional mayor que 3/2).
Construcciones
Los poliedros y teselaciones uniformes de Wythoff se pueden definir por su símbolo de Wythoff , que especifica la región fundamental del objeto. Una extensión de la notación de Schläfli , también utilizada por Coxeter , se aplica a todas las dimensiones; consiste en la letra 't', seguida de una serie de números subscritos correspondientes a los nodos anillados del diagrama de Coxeter , y seguida por el símbolo de Schläfli del politopo semilla regular. Por ejemplo, el octaedro truncado se representa mediante la notación: t 0,1 {3,4}.
| Operación | Símbolo de Schläfli | Diagrama de Coxeter | Símbolo de Wythoff | Posición:     | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
     |      |      |      |      |      | ||||||||
| Padre | {p,q} | t 0 {p,q} |      | q | 2 p | {pags} | { } | -- | -- | -- | { } | |||
| Birectificado (o dual ) | {q,p} | t2 {p , q} |      | p | 2 q | -- | { } | {q} | { } | -- | -- | |||
| Truncado | t{p,q} | t 0,1 {p,q} |      | 2 q | p | {2p} | { } | {q} | -- | { } | { } | |||
| Bitruncado (o dual truncado) | t{q,p} | t1,2 { p,q} |      | 2 p | q | {pags} | { } | {2q} | { } | { } | -- | |||
| Rectificado | r{p,q} | t1 {p , q} |    |      | 2 | pq | {pags} | -- | {q} | -- | { } | -- | ||
| Cantelado (o expandido ) | rr{p,q} | t 0,2 {p,q} |    |      | pq | 2 | {pags} | { }×{ } | {q} | { } | -- | { } | ||
| Cantitruncado (u Omnitruncado ) | tr{p,q} | t 0,1,2 {p,q} |    |      | 2 piezas | | {2p} | { }×{} | {2q} | { } | { } | { } | ||
| Operación | Símbolo de Schläfli | Diagrama de Coxeter | Símbolo de Wythoff | Posición:     | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
     |      |      |      |      |      | ||||||||
| Snub rectificado | sr{p,q} |    |      | | 2 uds. | {pags} | {3} {3} | {q} | -- | -- | -- | |||
| Desaire | s{p,2q} | alto 0,1 {p,q} |       | es{2p} | {3} | {q} | -- | {3} | |||||
 |  Generando triángulos |
Cuatro dimensiones
En cuatro dimensiones, hay 6 4-politopos regulares convexos , 17 prismas sobre los sólidos platónico y arquimediano (excluyendo el prisma cúbico, que ya se ha contado como teseracto ), y dos conjuntos infinitos: los prismas sobre los antiprismas convexos y los duoprismas . También hay 41 4-politopos semirregulares convexos, incluyendo el gran antiprisma no wythoffiano y el snub de 24 celdas . Ambos 4-politopos especiales están compuestos por subgrupos de los vértices del 600-cell .
No se han enumerado todos los politopos estelares uniformes de cuatro dimensiones. Entre los que sí se han enumerado se encuentran los 10 politopos estelares regulares (Schläfli-Hess) y los 57 prismas sobre los poliedros estelares uniformes, así como tres familias infinitas: los prismas sobre los antiprismas estelares, los duoprismas formados al multiplicar dos polígonos estelares y los duoprismas formados al multiplicar un polígono ordinario por un polígono estelar. Existe un número desconocido de politopos estelares que no encajan en las categorías anteriores; hasta ahora se han descubierto más de mil.

Hay 3 ángulos diedros rectos (2 espejos perpendiculares que se intersecan):
aristas 1 a 2, 0 a 2 y 1 a 3.

Cada politopo regular puede verse como la imagen de una región fundamental en un pequeño número de espejos. En un politopo de 4 dimensiones (o panal cúbico de 3 dimensiones) la región fundamental está limitada por cuatro espejos. Un espejo en el espacio de 4 dimensiones es un hiperplano tridimensional , pero es más conveniente para nuestros propósitos considerar solo su intersección bidimensional con la superficie tridimensional de la hiperesfera ; por lo tanto, los espejos forman un tetraedro irregular .
Cada uno de los dieciséis 4-politopos regulares es generado por uno de los cuatro grupos de simetría, como sigue:
- grupo [3,3,3]: las 5 celdas {3,3,3}, que son autoduales;
- grupo [3,3,4]: 16 celdas {3,3,4} y su teseracto dual {4,3,3};
- grupo [3,4,3]: el {3,4,3} de 24 celdas , autodual;
- grupo [3,3,5]: {3,3,5} de 600 celdas , su dual {5,3,3} de 120 celdas y sus diez estelaciones regulares.
- grupo [3 1,1,1 ]: contiene sólo miembros repetidos de la familia [3,3,4].
(Los grupos se nombran en notación Coxeter ).
Ocho de los panales uniformes convexos en el espacio 3-euclidiano se generan de forma análoga a partir del panal cúbico {4,3,4}, aplicando las mismas operaciones utilizadas para generar los 4-politopos uniformes wythoffianos.
Para un símplex de simetría dado, un punto generador puede ubicarse en cualquiera de los cuatro vértices, 6 aristas, 4 caras o el volumen interior. En cada uno de estos 15 elementos hay un punto cuyas imágenes, reflejadas en los cuatro espejos, son los vértices de un 4-politopo uniforme.
Los símbolos Schläfli extendidos se forman con una t seguida de la inclusión de uno a cuatro subíndices 0,1,2,3. Si hay un subíndice, el punto generador está en una esquina de la región fundamental, es decir, un punto donde se encuentran tres espejos. Estas esquinas se anotan como
- 0 : vértice del politopo 4 padre (centro de la celda dual)
- 1 : centro del borde del padre (centro de la cara del dual)
- 2 : centro de la cara del padre (centro del borde del dual)
- 3 : centro de la celda del padre (vértice del dual)
(Para los dos 4-politopos autoduales, "dual" significa un 4-politopo similar en posición dual). Dos o más subíndices significan que el punto generador está entre las esquinas indicadas.
Resumen constructivo
A continuación se resumen las 15 formas constructivas por familia. Las familias autoduales se enumeran en una columna y las demás en dos columnas con entradas compartidas en los diagramas de Coxeter simétricos . La décima fila final enumera las construcciones de 24 celdas con forma de snub. Esto incluye todos los 4-politopos uniformes no prismáticos, excepto el gran antiprisma no wythoffiano , que no tiene familia Coxeter.
Formas truncadas
La siguiente tabla define 15 formas de truncamiento. Cada forma puede tener de uno a cuatro tipos de celdas, ubicadas en las posiciones 0, 1, 2 y 3, como se definió anteriormente. Las celdas están etiquetadas mediante notación de truncamiento poliédrico.
- Un prisma n -gonal se representa como: {n}×{ }.
- El fondo verde se muestra en los formularios que son equivalentes al padre o al dual.
- El fondo rojo muestra los truncamientos del padre, y el azul los truncamientos del dual.
| Operación | Símbolo de Schläfli | Diagrama de Coxeter | Celdas por posición:       | ||||
|---|---|---|---|---|---|---|---|
(3)       | (2)       | (1)       | (0)       | ||||
| Padre | {p,q,r} | t 0 {p, q, r} |        |      {p,q} |      -- |      -- |      -- |
| Rectificado | r{p,q,r} | t1 {p,q,r } |        |      r{p,q} |      -- |      -- |      {q,r} |
| Birectificado (o rectificado dual) | 2r{p,q,r} = r{r,q,p} | t2 {p, q ,r} |        |      {q,p} |      -- |      -- |      r{q,r} |
| Trirectificado (o dual ) | 3r{p,q,r} = {r,q,p} | t3 {p,q,r } |        |      -- |      -- |      -- |      {r,q} |
| Truncado | t{p,q,r} | t 0,1 {p,q,r} |        |      t{p,q} |      -- |      -- |      {q,r} |
| Bittruncado | 2t{p,q,r} | 2t{p,q,r} |        |      t{q,p} |      -- |      -- |      t{q,r} |
| Tritruncado (o dual truncado) | 3t{p,q,r} = t{r,q,p} | t2,3 {p, q ,r} |        |      {q,p} |      -- |      -- |      t{r,q} |
| Cantelado | rr{p,q,r} | t 0,2 {p,q,r} |        |      rr{p,q} |      -- |      { }×{r} |      r{q,r} |
| Bicantelada (o dual cantelada) | r2r{p,q,r} = rr{r,q,p} | t 1,3 {p,q,r} |        |      r{p,q} |      {p}×{ } |      -- |      rr{q,r} |
| Runcinado (o expandido ) | e{p,q,r} | t 0,3 {p,q,r} |        |      {p,q} |      {p}×{ } |      { }×{r} |      {r,q} |
| Cantitruncado | tr{p,q,r} | tr{p,q,r} |        |      tr{p,q} |      -- |      { }×{r} |      t{q,r} |
| Bicantitruncado (o cantitruncado dual) | t2r{p,q,r} = tr{r,q,p} | t 1,2,3 {p,q,r} |        |      t{q,p} |      {p}×{ } |      -- |      tr{q,r} |
| Runcitruncado | y t {p,q,r} | t 0,1,3 {p,q,r} |        |      t{p,q} |      {2p}×{ } |      { }×{r} |      rr{q,r} |
| Runcicantelado (o runcitruncado dual) | e 3t {p,q,r} = e t {r,q,p} | t 0,2,3 {p,q,r} |        |      tr{p,q} |      {p}×{ } |      { }×{2r} |      t{r,q} |
| Runcicantitruncado (u omnitruncado ) | o{p,q,r} | t 0,1,2,3 {p,q,r} |        |      tr{p,q} |      {2p}×{ } |      { }×{2r} |      tr{q,r} |
Formas a medias
Existen semiconstrucciones con agujeros en lugar de nodos en forma de anillo. Las ramas vecinas a los agujeros y a los nodos inactivos deben ser de orden par. Las semiconstrucciones tienen los vértices de una construcción en forma de anillo idéntica.
| Operación | Símbolo de Schläfli | Diagrama de Coxeter | Celdas por posición:       | ||||
|---|---|---|---|---|---|---|---|
(3)       | (2)       | (1)       | (0)       | ||||
| Medio alternado | h{p,2q,r} | alto 0 {p,2q,r} |         |       h{p,2q} |       -- |      -- |      -- |
| Alternado rectificado | hr{2p,2q,r} | alto 1 {2p,2q,r} |          |        hora{2p,2q} |       -- |      -- |      h{2q,r} |
Truncamiento alterno de Snub | s{p,2q,r} | alto 0,1 {p,2q,r} |         |       s{p,2q} |      -- |      -- |       h{2q,r} |
| Bisnub Truncamiento de bits alternado | 2s{2p,q,2r} | alto 1,2 {2p,q,2r} |          |       s{q,2p} |       -- |       -- |       s{q,2r} |
| Rectificado snub Alternado truncado rectificado | sr{p,q,2r} | alto 0,1,2 {p,q,2r} |         |      sr{p,q} |      -- |       s{2,2r} |       s{q,2r} |
| Omnisnub Truncamiento alterno | sistema operativo {p,q,r} | alto 0,1,2,3 {p,q,r} |        |      sr{p,q} |      {p}×{ } |      { }×{r} |      sr{q,r} |
Cinco dimensiones y más
En cinco dimensiones y superiores, hay tres politopos regulares: el hipercubo , el símplex y el politopo cruzado . Son generalizaciones del cubo tridimensional, el tetraedro y el octaedro, respectivamente. No hay politopos regulares en forma de estrella en estas dimensiones. La mayoría de los politopos uniformes de dimensiones superiores se obtienen modificando los politopos regulares o tomando el producto cartesiano de politopos de dimensiones inferiores.
En seis, siete y ocho dimensiones, entran en juego los excepcionales grupos de Lie simples , E 6 , E 7 y E 8 . Colocando anillos en un número distinto de cero de nodos de los diagramas de Coxeter , se pueden obtener 39 nuevos 6-politopos, 127 nuevos 7-politopos y 255 nuevos 8-politopos. Un ejemplo notable es el politopo 4 21 .
Panales uniformes
Relacionados con el tema de los politopos finitos uniformes están los panales uniformes en espacios euclidianos e hiperbólicos. Los panales uniformes euclidianos son generados por grupos de Coxeter afines y los panales hiperbólicos son generados por los grupos de Coxeter hiperbólicos . Dos grupos de Coxeter afines pueden ser multiplicados entre sí.
Existen dos clases de grupos de Coxeter hiperbólicos: compactos y paracompactos. Los panales uniformes generados por grupos compactos tienen facetas y figuras de vértice finitas y existen en 2 a 4 dimensiones. Los grupos paracompactos tienen subgrafos afines o hiperbólicos y facetas o figuras de vértice infinitas y existen en 2 a 10 dimensiones.
Véase también
Referencias
- Coxeter La belleza de la geometría: doce ensayos , Dover Publications, 1999, ISBN 978-0-486-40919-1 (Capítulo 3: Construcción de Wythoff para politopos uniformes)
- Manuscrito de politopos uniformes de Norman Johnson (1991)
- Norman Johnson: La teoría de los politopos uniformes y los panales de abejas , tesis doctoral, Universidad de Toronto, 1966 EN LÍNEA
- A. Boole Stott : Deducción geométrica de politopos semirregulares a partir de regulares y rellenos espaciales , Verhandelingen de la unidad de ancho de la academia Koninklijke van Wetenschappen Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910 PDF
- HSM Coxeter :
- HSM Coxeter, MS Longuet-Higgins y JCP Miller: Poliedros uniformes , Philosophical Transactions de la Royal Society de Londres, Londres, 1954 PDF
- HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II, [Math. Zeit. 188 (1985) 559-591]
- (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III, [Math. Zeit. 200 (1988) 3-45]
- Marco Möller, Vierdimensionale Archimedische Polytope , Disertación, Universität Hamburg, Hamburgo (2004) (en alemán) ONLINE
Enlaces externos
- Olshevsky, George. «Polítopo uniforme». Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
- Politopos uniformes y convexos en cuatro dimensiones:, Marco Möller (en alemán)