Truncamiento (geometría)

El cuadrado truncado es un octágono regular: t{4} = {8} =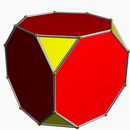

Cubo truncado t{4,3} o

Panal cúbico truncado t{4,3,4} o

En geometría , un truncamiento es una operación en cualquier dimensión que corta los vértices de un politopo , creando una nueva faceta en lugar de cada vértice. El término tiene su origen en los nombres que Kepler le dio a los sólidos de Arquímedes .

En general, cualquier poliedro (o politopo) también se puede truncar con un grado de libertad en cuanto a la profundidad del corte, como se muestra en la operación de truncamiento de notación de poliedro de Conway .

Un tipo especial de truncamiento, generalmente implícito, es el truncamiento uniforme , un operador de truncamiento aplicado a un poliedro regular (o politopo regular ) que crea un poliedro uniforme resultante ( politopo uniforme ) con longitudes de aristas iguales. No hay grados de libertad y representa una geometría fija, al igual que los poliedros regulares.

En general, todos los politopos uniformes de un solo anillo tienen un truncamiento uniforme. Por ejemplo, el icosidodecaedro , representado por los símbolos de Schläfli r{5,3} o , y el diagrama de Coxeter-Dynkin${\displaystyle {\begin{Bmatrix}5\\3\end{Bmatrix}}}$ otiene un truncamiento uniforme, el icosidodecaedro truncado , representado como tr{5,3} o ,${\displaystyle t{\begin{Bmatrix}5\\3\end{Bmatrix}}}$En el diagrama de Coxeter-Dynkin , el efecto de un truncamiento es rodear con un anillo todos los nodos adyacentes al nodo rodeado con un anillo.

Un truncamiento uniforme realizado en el mosaico triangular regular {3,6} da como resultado el mosaico hexagonal regular {6,3}.

Un polígono truncado de n lados tendrá 2n lados (aristas). Un polígono regular truncado uniformemente se convertirá en otro polígono regular: t{n} es {2n}. Un truncamiento completo (o rectificación ), r{3}, es otro polígono regular en su posición dual .

Un polígono regular también se puede representar mediante su diagrama de Coxeter-Dynkin ,, y su truncamiento uniforme, y su truncamiento completo. El gráficorepresenta el grupo de Coxeter I ₂ (n), donde cada nodo representa un espejo y el borde representa el ángulo π/ n entre los espejos, y se da un círculo alrededor de uno o ambos espejos para mostrar cuáles están activos.

Truncamientos paramétricos de un triángulo

{3}

t{3} = {6}

r{3} = {3}

Los polígonos estrellados también pueden truncarse. Un pentagrama truncado {5/2} parecerá un pentágono , pero en realidad es un decágono doblemente cubierto (degenerado) ({10/2}) con dos conjuntos de vértices y aristas superpuestos. Un gran heptagrama truncado {7/3} da como resultado un tetradecagrama {14/3}.

Cuando "truncamiento" se aplica a sólidos platónicos o teselas regulares , generalmente se implica "truncamiento uniforme", lo que significa truncar hasta que las caras originales se conviertan en polígonos regulares con el doble de lados que la forma original.

Esta secuencia muestra un ejemplo del truncamiento de un cubo, utilizando cuatro pasos de un proceso de truncamiento continuo entre un cubo completo y un cubo rectificado . El poliedro final es un cuboctaedro . La imagen del medio es el cubo truncado uniforme ; está representado por un símbolo de Schläfli t { p , q ,...}.

Un bitruncado es un truncamiento más profundo, que elimina todas las aristas originales, pero deja una parte interior de las caras originales. Ejemplo: un octaedro truncado es un cubo bitruncado: t{3,4} = 2t{4,3}.

Una birectificación completa, llamada bitruncamiento , reduce las caras originales a puntos. En el caso de los poliedros, esto se convierte en el poliedro dual . Ejemplo: un octaedro es una birectificación de un cubo : {3,4} = 2r{4,3}.

Otro tipo de truncamiento, la cantelación , corta aristas y vértices, eliminando las aristas originales, reemplazándolas con rectángulos, eliminando los vértices originales y reemplazándolos con las caras del dual de los poliedros regulares originales o teselación.

Los politopos de dimensiones superiores tienen truncamientos mayores. La runcinación corta caras, aristas y vértices. En 5 dimensiones, la esterificación corta celdas, caras y aristas.

El truncamiento de aristas es un biselado o chaflán para poliedros, similar a la cantelación, pero conservando los vértices originales y reemplazando las aristas por hexágonos. En los 4-politopos, el truncamiento de aristas reemplaza las aristas por celdas bipiramidales alargadas .

La alternancia o truncamiento parcial elimina sólo algunos de los vértices originales.

En el truncamiento parcial , o alternancia , se eliminan por completo la mitad de los vértices y las aristas de conexión. La operación se aplica solo a politopos con caras de lados pares. Las caras se reducen a la mitad de sus lados y las caras cuadradas degeneran en aristas. Por ejemplo, el tetraedro es un cubo alternado, h{4,3}.

La disminución es un término más general que se utiliza en referencia a los sólidos de Johnson para referirse a la eliminación de uno o más vértices, aristas o caras de un politopo, sin alterar los demás vértices. Por ejemplo, el icosaedro tridisminuido comienza con un icosaedro regularal que se le han eliminado tres vértices.

Otros truncamientos parciales se basan en la simetría; por ejemplo, el dodecaedro tetraédricamente disminuido .

El proceso de truncamiento lineal se puede generalizar permitiendo truncamientos paramétricos que sean negativos, o que vayan más allá del punto medio de los bordes, causando poliedros estelares autointersecantes, y pueden relacionarse paramétricamente con algunos de los polígonos estelares regulares y poliedros estelares uniformes .

• Truncamiento superficial : las aristas se reducen en longitud, las caras se truncan para tener el doble de lados, mientras se forman nuevas facetas , centradas en los vértices antiguos.
• El truncamiento uniforme es un caso especial de esto con longitudes de aristas iguales. El cubo truncado , t{4,3}, con caras cuadradas que se convierten en octógonos, con nuevas caras triangulares que son los vértices.
• Antitruncamiento Un truncamiento superficial inverso , truncado hacia afuera de los bordes originales, en lugar de hacia adentro. Esto da como resultado un politopo que se parece al original, pero tiene partes del dual colgando de sus esquinas, en lugar de que el dual se corte en sus propias esquinas.
• Truncamiento o rectificación completa : límite de un truncamiento superficial, en el que las aristas se reducen a puntos. El cuboctaedro , r{4,3}, es un ejemplo.
• Hipertruncamiento Una forma de truncamiento que va más allá de la rectificación, invirtiendo los bordes originales y provocando la aparición de autointersecciones.
• Cuasitruncamiento Una forma de truncamiento que va incluso más allá que el hipertruncamiento donde el borde invertido se vuelve más largo que el borde original. Se puede generar a partir del politopo original tratando todas las caras como retrógradas, es decir, yendo hacia atrás alrededor del vértice. Por ejemplo, cuasitruncar el cuadrado da un octagrama regular (t{4,3}={8/3}), y cuasitruncar el cubo da el hexaedro truncado estrellado uniforme , t{4/3,3}.

Truncamientos en un cuadrado

Tipos de truncamiento en un cuadrado, {4}, que muestran los bordes originales en rojo y los nuevos bordes truncados en cian. Un cuadrado truncado uniforme es un octógono regular, t{4}={8}. Un cuadrado truncado completo se convierte en un nuevo cuadrado, con una orientación diagonal. Los vértices se ordenan en sentido antihorario, 1-4, con pares de vértices truncados como a y b .

Truncamientos del cubo

⇨ taC	Cubo {4,3} C	⇨ tC	Truncamiento t{4,3} tC	⇨ tC	Truncamiento completo r{4,3} aC	⇩ el C
TaC antitruncamiento						Hipertruncamiento thC
⇧ taC	Cuasitruncamiento completo aqC	⇦	Cuasitruncamiento t{4/3,3} tqC	⇦ tqc	Hipertruncamiento completo ahC	⇦ el C.

• Poliedro uniforme
• Politopo 4 uniforme
• Bittruncamiento (geometría)
• Rectificación (geometría)
• Alternancia (geometría)
• Notación del poliedro de Conway
• Cono truncado

• Coxeter, HSM Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN  0-486-61480-8 (págs. 145-154 Capítulo 8: Truncamiento)
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson : La teoría de los politopos uniformes y los panales de abejas , tesis doctoral, Universidad de Toronto, 1966

• Weisstein, Eric W. "Truncamiento". MathWorld .
• Olshevsky, George. "Truncation". Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
• Nombres de poliedros, truncamiento

Operadores de poliedro

• en
• a
• mi

Semilla	Truncamiento	Rectificación	Truncamiento de bits	Dual	Expansión	Omnitruncamiento	Alternancias
t 0 { p , q } { p , q }	t 01 { p , q } t{ p , q }	t 1 { p , q } r{ p , q }	t 12 { p , q } 2t{ p , q }	t 2 { p , q } 2r{ p , q }	t 02 { p , q } rr{ p , q }	t 012 { p , q } tr{ p , q }	ht 0 { p , q } h{ q , p }	ht 12 { p , q } s{ q , p }	ht 012 { p , q } sr{ p , q }