Icosidodecaedro
Sólido arquimediano con 32 caras
Icosidodecaedro
TipoSólido arquimediano
Poliedro uniforme
Poliedro cuasirregular
Caras32
Bordes60
Vértices30
Grupo de simetríaSimetría icosaédrica I yo {\displaystyle \mathrm {I} _ {\mathrm {h} }}
Angulo diedro ( grados )142,62°
Poliedro dualTriacontaedro rómbico
Propiedadesconvexo
Figura de vértice
Neto
Modelo 3D de un icosidodecaedro

En geometría , un icosidodecaedro o girobirrotonda pentagonal es un poliedro con veinte caras triangulares ( icosi ) y doce caras pentagonales ( dodeca ) . Un icosidodecaedro tiene 30 vértices idénticos , con dos triángulos y dos pentágonos que se encuentran en cada uno, y 60 aristas idénticas, cada una de las cuales separa un triángulo de un pentágono. Como tal, es uno de los sólidos arquimedianos y, más particularmente, un poliedro cuasirregular .

Construcción

Una forma de construir el icosidodecaedro es comenzar con dos rotondas pentagonales uniéndolas a sus bases. Estas rotondas cubren su base decagonal de modo que el poliedro resultante tiene 32 caras, 30 vértices y 60 aristas. Esta construcción es similar a uno de los sólidos de Johnson , la ortobirotonda pentagonal . La diferencia es que el icosidodecaedro se construye girando sus rotondas 36°, un proceso conocido como giro , lo que da como resultado que la cara pentagonal se conecte con la triangular. El icosidodecaedro tiene un nombre alternativo, girobirotonda pentagonal . [1] [2]

La diferencia entre icosidodecaedro y ortobirotonda pentagonal, y su disección.

Las coordenadas cartesianas convenientes para los vértices de un icosidodecaedro con aristas unitarias se dan mediante las permutaciones pares de: donde denota la proporción áurea . [3] ( 0 , 0 , ± φ ) , ( ± 1 2 , ± φ 2 , ± φ 2 2 ) , {\displaystyle (0,0,\pm \varphi ),\qquad \left(\pm {\frac {1}{2}},\pm {\frac {\varphi }{2}},\pm {\frac {\varphi ^{2}}{2}}\right),} φ {\estilo de visualización \varphi}

Propiedades

El área de la superficie de un icosidodecaedro se puede determinar calculando el área de todas las caras pentagonales. El volumen de un icosidodecaedro se puede determinar dividiendo el icosidodecaedro en dos caras pentagonales y sumando sus volúmenes. Por lo tanto, su área de superficie y su volumen se pueden formular como: [1] A {\estilo de visualización A} V {\estilo de visualización V} A = ( 5 3 + 3 25 + 10 5 ) a 2 ≈ 29.306 a 2 V = 45 + 17 5 6 a 3 ≈ 13.836 a 3 . {\displaystyle {\begin{aligned}A&=\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}&\approx 29.306a^{2}\\V&={\frac {45+17{\sqrt {5}}}{6}}a^{3}&\approx 13.836a^{3}.\end{aligned}}}

El ángulo diedro de un icosidodecaedro entre pentágono y triángulo se determina calculando el ángulo de una rotonda pentagonal. [4] arcos ⁡ ( − 5 + 2 5 15 ) ≈ 142,62 ∘ , {\displaystyle \arccos \left(-{\sqrt {\frac {5+2{\sqrt {5}}}{15}}}\right)\aproximadamente 142,62^{\circ },}

Un icosidodecaedro tiene simetría icosaédrica , y su primera estelación es la compuesta de un dodecaedro y su icosaedro dual , con los vértices del icosidodecaedro ubicados en los puntos medios de las aristas de cualquiera de ellos.

El icosidodecaedro es un sólido arquimediano , es decir, un poliedro altamente simétrico y semirregular, y dos o más caras poligonales regulares diferentes se encuentran en un vértice. [5] Las caras poligonales que se encuentran en cada vértice son dos triángulos equiláteros y dos pentágonos regulares, y la figura del vértice de un icosidodecaedro es . Su poliedro dual es el triacontaedro rómbico , un sólido catalán . [4] ( 3 ⋅ 5 ) 2 = 3 2 ⋅ 5 2 {\displaystyle (3\cdot 5)^{2}=3^{2}\cdot 5^{2}}

Las 60 aristas forman 6 decágonos correspondientes a círculos máximos en el mosaico esférico.

El icosidodecaedro tiene 6 decágonos centrales que , proyectados en una esfera, definen 6 círculos máximos . Fuller (1975) utilizó estos 6 círculos máximos, junto con otros 15 y 10 más en otros dos poliedros para definir sus 31 círculos máximos del icosaedro esférico . [6]

El radio largo (centro a vértice) del icosidodecaedro está en la proporción áurea con respecto a la longitud de su arista; por lo tanto, su radio es si la longitud de su arista es 1, y su longitud de arista es si su radio es 1. [4] Solo unos pocos politopos uniformes tienen esta propiedad, incluido el politopo de 600 celdas de cuatro dimensiones , el politopo de 600 celdas de tres dimensiones y el politopo de 600 celdas de dos dimensiones . (El politopo de 600 celdas de cuatro dimensiones es la sección transversal ecuatorial del politopo de 600 celdas de tres dimensiones y el politopo de 600 celdas de dos dimensiones.) Estos politopos radialmente áureos se pueden construir, con sus radios, a partir de triángulos áureos que se encuentran en el centro, cada uno de los cuales contribuye con dos radios y una arista. φ {\estilo de visualización \varphi} 1 / φ {\estilo de visualización 1/\varphi}

El icosidodecaedro es un dodecaedro rectificado y también un icosaedro rectificado , que existe como el truncamiento de arista completa entre estos sólidos regulares.

El icosidodecaedro contiene 12 pentágonos del dodecaedro y 20 triángulos del icosaedro :

Familia de poliedros icosaédricos uniformes
Simetría : [5,3] , (*532)[5,3] + , (532)
{5,3}t{5,3}r{5,3}t{3,5}{3,5}rr{5,3}tr{5,3}sr{5,3}
De poliedros duales a uniformes
V5.5.5V3.10.10V3.5.3.5V5.6.6V3.3.3.3.3V3.4.5.4V4.6.10V3.3.3.3.5

El icosidodecaedro existe en una secuencia de simetrías de poliedros cuasirregulares y teselas con configuraciones de vértice (3. n ) 2 , que progresan desde teselas de la esfera hasta el plano euclidiano y al plano hiperbólico. Con una simetría de notación orbifold de * n 32 todas estas teselas son construcciones de Wythoff dentro de un dominio fundamental de simetría, con puntos generadores en la esquina del ángulo recto del dominio. [7] [8]

* n 32 simetrías orbifold de teselaciones cuasirregulares : (3. n ) 2

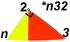Construcción		EsféricoEuclidianoHiperbólico
*332*432*532*632*732*832...*∞32

Figuras cuasirregulares
Vértice(3.3) 2(3.4) 2(3.5)2(3.6) 2(3.7) 2(3.8) 2(3.∞) 2
*5 n 2 mutaciones de simetría de teselaciones cuasirregulares: (5.n) 2
Simetría
*5 n 2
[n,5]		EsféricoHiperbólicoParacompactoNo compacto
*352
[3,5]		*452
[4,5]		*552
[5,5]		*652
[6,5]		*752
[7,5]		*852
[8,5]...		*∞52
[∞,5]		 
[ n i,5]
Cifras
Configuración.(5.3)2(5.4) 2(5.5) 2(5.6) 2(5.7)2(5.8)2(5.∞) 2(5. n i) 2

Figuras rómbicas
Configuración.V(5.3) 2V(5.4) 2V(5,5) 2V(5.6) 2V(5.7) 2V(5.8) 2V(5.∞) 2V(5.∞) 2
Un icosidodecaedro topológico en cubo truncado, insertando 6 vértices en el centro de octógonos y diseccionándolos en 2 pentágonos y 2 triángulos.

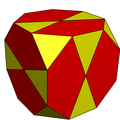
El cubo truncado se puede transformar en un icosidodecaedro dividiendo los octógonos en dos pentágonos y dos triángulos. Tiene simetría piritoédrica .

Ocho poliedros estrellados uniformes comparten la misma disposición de vértices . De ellos, dos también comparten la misma disposición de aristas : el pequeño icosihemidodecaedro (que tiene las caras triangulares en común) y el pequeño dodecahemidodecaedro (que tiene las caras pentagonales en común). La disposición de vértices también la comparten los compuestos de cinco octaedros y de cinco tetrahemihexaedros .


Icosidodecaedro
Icosihemidodecaedro pequeño
Dodecahemidodecaedro pequeño

Gran icosidodecaedro
Gran dodecahemidodecaedro
Gran icosihemidodecaedro

Dodecadodecaedro
Dodecaedro hemicosaedro pequeño
Gran dodecahemicosaedro

Compuesto de cinco octaedros
Compuesto de cinco tetrahemihexaedros

En la geometría de cuatro dimensiones, el icosidodecaedro aparece en la celda regular de 600 como la porción ecuatorial que pertenece al paso del vértice primero de la celda de 600 a través del espacio 3D. En otras palabras: los 30 vértices de la celda de 600 que se encuentran a distancias de arco de 90 grados en su hiperesfera circunscrita de un par de vértices opuestos, son los vértices de un icosidodecaedro. La figura de estructura alámbrica de la celda de 600 consta de 72 decágonos regulares planos. Seis de ellos son los decágonos ecuatoriales de un par de vértices opuestos, y estos seis forman la figura de estructura alámbrica de un icosidodecaedro.

Si se proyecta estereográficamente una celda de 600 en un espacio tridimensional alrededor de cualquier vértice y se normalizan todos los puntos, las geodésicas sobre las que caen los bordes comprenden la subdivisión baricéntrica del icosidodecaedro .

Gráfico

La gráfica de un icosidodecaedro

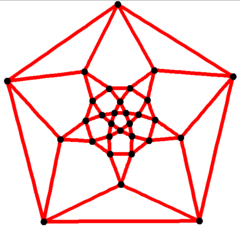
El esqueleto de un icosidodecaedro puede representarse como un grafo de 30 vértices y 60 aristas, uno de los grafos arquimedianos . Es de orden cuártico , es decir, cada uno de sus vértices está conectado por otros cuatro vértices. [9]

Apariencia

El icosidodecaedro puede aparecer en estructuras, como en la cúpula geodésica de la esfera de Hoberman .

Los icosidodecaedros se pueden encontrar en todas las células eucariotas, incluidas las células humanas, como formaciones de proteína de cubierta Sec13/31 COPII . [10]

El icosidodecaedro también puede encontrarse en la cultura popular. En el universo de Star Trek , el juego de lógica vulcaniano Kal-Toh tiene como objetivo crear una forma con dos icosidodecaedros holográficos anidados unidos en los puntos medios de sus segmentos.

Véase también

Referencias

  1. ^ ab Berman, Martin (1971). "Poliedros convexos de caras regulares". Revista del Instituto Franklin . 291 (5): 329–352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
  2. ^ Ogievetsky, O.; Shlosman, S. (2021). "Compuestos y cilindros platónicos". En Novikov, S.; Krichever, I.; Ogievetsky, O.; Shlosman, S. (eds.). Integrabilidad, cuantificación y geometría: II. Teorías cuánticas y geometría algebraica. American Mathematical Society . pág. 477. ISBN 978-1-4704-5592-7.
  3. ^ Weisstein, Eric W. "Grupo icosaédrico". MathWorld .
  4. ^ abc Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño. Dover Publications, Inc. pág. 86. ISBN 978-0-486-23729-9.
  5. ^ Diudea, MV (2018). Cúmulos poliédricos de múltiples capas. Materiales de carbono: química y física. Vol. 10. Springer . p. 39. doi :10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
  6. ^ Fuller, RB (1975). Sinergética: exploraciones en la geometría del pensamiento. MacMillan. pág. 183-185. ISBN. 978-0-02-065320-2.
  7. ^ Polítopos regulares de Coxeter , tercera edición (1973), edición Dover, ISBN 0-486-61480-8 (Capítulo V: El caleidoscopio, Sección: 5.7 Construcción de Wythoff) 
  8. ^ Mutaciones de simetría bidimensional de Daniel Huson
  9. ^ Read, RC; Wilson, RJ (1998), Un atlas de gráficos , Oxford University Press , pág. 269
  10. ^ Russell, Christopher; Stagg, Scott (11 de febrero de 2010). "Nuevos conocimientos sobre los mecanismos estructurales de la capa de COPII". Traffic . 11 (3): 303–310. doi : 10.1111/j.1600-0854.2009.01026.x . PMID  20070605.
  • Cromwell, P. (1997). Poliedros . Reino Unido: Cambridge. pp. 79–86. Sólidos arquimedianos . ISBN . 0-521-55432-2.
  • Weisstein, Eric W. , "Icosidodecaedro" ("Sólido arquimediano") en MathWorld .
  • Klitzing, Richard. "Poliedros uniformes convexos 3D o3x5o - id".
  • Red editable e imprimible de un icosidodecaedro con vista 3D interactiva
  • Los poliedros uniformes
  • Poliedros de realidad virtual La enciclopedia de poliedros
Obtenido de "https://es.wikipedia.org/w/index.php?title=Icosidodecaedro&oldid=1245430667"