Icosidodecaedro truncado

Icosidodecaedro truncado
(Haga clic aquí para ver el modelo rotatorio)
Tipo	Sólido arquimediano Poliedro uniforme
Elementos	F = 62, E = 180, V = 120 (χ = 2)
Caras por lados	30{4}+20{6}+12{10}
Notación de Conway	bD o taD
Símbolos de Schläfli	tr{5,3} o${\displaystyle t{\begin{Bmatrix}5\\3\end{Bmatrix}}}$
	t0,1,2 { 5,3}
Símbolo de Wythoff	2 3 5 |
Diagrama de Coxeter
Grupo de simetría	I h , H 3 , [5,3], (*532), orden 120
Grupo de rotación	Yo , [5,3] + , (532), orden 60
Ángulo diedro	6-10: 142,62° 4-10: 148,28° 4-6: 159,095°
Referencias	U 28 , C 31 , O 16
Propiedades	Zonohedro convexo semirregular
Caras de colores	4.6.10 ( Figura de vértice )
Triacontaedro de Disdyakis ( poliedro dual )	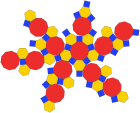Neto

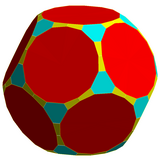
En geometría , un icosidodecaedro truncado , icosidodecaedro rombitruncado , ^[1] gran rombicosidodecaedro , ^{[2] [3]} dodecaedro omnitruncado o icosaedro omnitruncado ^[4] es un sólido arquimediano , uno de los trece sólidos convexos , isogonales y no prismáticos construidos por dos o más tipos de caras de polígonos regulares .

Tiene 62 caras: 30 cuadrados , 20 hexágonos regulares y 12 decágonos regulares . Tiene la mayor cantidad de aristas y vértices de todos los sólidos platónicos y arquimedianos, aunque el dodecaedro romo tiene más caras. De todos los poliedros transitivos por vértices, ocupa el mayor porcentaje (89,80%) del volumen de una esfera en la que está inscrito , superando muy de cerca al dodecaedro romo (89,63%) y al pequeño rombicosidodecaedro (89,23%), y superando menos de cerca al icosaedro truncado (86,74%); También tiene, con diferencia, el mayor volumen (206,8 unidades cúbicas) cuando la longitud de su arista es igual a 1. De todos los poliedros transitivos de vértice que no son prismas o antiprismas , tiene la mayor suma de ángulos (90 + 120 + 144 = 354 grados) en cada vértice; solo un prisma o antiprisma con más de 60 lados tendría una suma mayor. Dado que cada una de sus caras tiene simetría puntual (equivalentemente, simetría rotacional de 180° ), el icosidodecaedro truncado es un 15 -zonoedro .

El nombre de gran rombicosidodecaedro hace referencia a la relación con el (pequeño) rombicosidodecaedro (compárese con la sección Disección).
Existe un poliedro uniforme no convexo con un nombre similar, el gran rombicosidodecaedro no convexo .

El área superficial A y el volumen V del icosidodecaedro truncado de longitud de arista a son: ^{[ cita requerida ]}

${\displaystyle {\begin{aligned}A&=30\left(1+{\sqrt {3}}+{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}&&\approx 174.292\,0303a^{2}.\\V&=\left(95+50{\sqrt {5}}\right)a^{3}&&\approx 206.803\,399a^{3}.\end{aligned}}}$

Si se construyera un conjunto de los 13 sólidos arquimedianos con todas las longitudes de arista iguales, el icosidodecaedro truncado sería el más grande.

Las coordenadas cartesianas de los vértices de un icosidodecaedro truncado con longitud de arista 2 φ  − 2, centrado en el origen, son todas las permutaciones pares de: ^[5]

(± ⁠1/φ⁠ , ± ⁠1/φ⁠ , ±(3 +  φ )),

(± ⁠2/φ⁠ , ± φ , ±(1 + 2 φ )),

(± ⁠1/φ⁠ , ± φ ² , ±(−1 + 3 φ )),

(±(2 φ  − 1), ±2, ±(2 +  φ )) y

(± φ , ±3, ±2φ ) ,

donde φ  =  ⁠1 + √ 5/2⁠ es la proporción áurea .

El icosidodecaedro truncado es la envoltura convexa de un rombicosidodecaedro con cuboides por encima de sus 30 cuadrados, cuya razón altura-base es φ . El resto de su espacio puede diseccionarse en cúpulas no uniformes, a saber, 12 entre pentágonos interiores y decágonos exteriores y 20 entre triángulos interiores y hexágonos exteriores .

Una disección alternativa también tiene un núcleo rombicosidodecaédrico. Tiene 12 rotondas pentagonales entre pentágonos internos y decágonos externos. La parte restante es un poliedro toroidal .

imágenes de disección
Estas imágenes muestran el rombicosidodecaedro (violeta) y el icosidodecaedro truncado (verde). Si las longitudes de sus aristas son 1, la distancia entre los cuadrados correspondientes es φ .

El icosidodecaedro truncado tiene siete proyecciones ortogonales especiales , centradas en un vértice, sobre tres tipos de aristas y tres tipos de caras: cuadrada, hexagonal y decagonal. Las dos últimas corresponden a los planos de Coxeter A ₂ y H ₂ .

Proyecciones ortogonales

Centrado por	Vértice	Borde 4-6	Filo 4-10	Borde 6-10	Cara cuadrada	Hexágono de cara	Decágono de cara
Sólido
Estructura alámbrica
Simetría proyectiva	[2] +	[2]	[2]	[2]	[2]	[6]	[10]
Imagen dual

El icosidodecaedro truncado también puede representarse como un mosaico esférico y proyectarse sobre el plano mediante una proyección estereográfica . Esta proyección es conforme y conserva los ángulos, pero no las áreas ni las longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Los diagramas de Schlegel son similares, con una proyección en perspectiva y bordes rectos.

Proyección ortográfica	Proyecciones estereográficas
	Centrado en el decágono	Centrado en hexágono	Centrado en el cuadrado

Dentro de la simetría icosaédrica existen ilimitadas variaciones geométricas del icosidodecaedro truncado con caras isogonales . El dodecaedro truncado , el rombicosidodecaedro y el icosaedro truncado como casos límites degenerados.

Grafo icosidodecaédrico truncado
Simetría quíntuple
Vértices	120
Bordes	180
Radio	15
Diámetro	15
Circunferencia	4
Automorfismos	120 (A5 × 2)
Número cromático	2
Propiedades	Cúbico , hamiltoniano , regular , cero-simétrico
Tabla de gráficos y parámetros

En el campo matemático de la teoría de grafos , un grafo icosidodecaédrico truncado (o gran grafo rombicosidodecaédrico ) es el grafo de vértices y aristas del icosidodecaedro truncado, uno de los sólidos arquimedianos . Tiene 120 vértices y 180 aristas, y es un grafo arquimediano cúbico y de simetría cero . ^[6]

Gráficos de diagramas de Schlegel

Simetría triple

Simetría doble

El icosaedro y el dodecaedro Bowtie contienen dos caras trapezoidales en lugar del cuadrado. [7]

Familia de poliedros icosaédricos uniformes
Simetría : [5,3] , (*532)							[5,3] + , (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
De poliedros duales a uniformes
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Este poliedro puede considerarse miembro de una secuencia de patrones uniformes con figura de vértice (4.6.2 p ) y diagrama de Coxeter-Dynkin Para p  < 6, los miembros de la secuencia son poliedros omnitruncados ( zonoedros ), que se muestran a continuación como teselas esféricas. Para p  > 6, son teselas del plano hiperbólico, comenzando con la tesela triheptagonal truncada .

* n 32 mutación de simetría de teselaciones omnitruncadas: 4.6.2n en a mi
Sím. * n 32 [ n ,3]	Esférico				Euclides.	Hiperb. compacta.		Paraíso.	Hiperbólica no compacta
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Cifras
Configuración.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Configuración.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	Versión 4.6.24i	Versión 4.6.18i	Versión 4.6.12i	Versión 4.6.6i

• Wenninger, Magnus (1974), Modelos de poliedros , Cambridge University Press , ISBN 978-0-521-09859-5, Sr.  0467493
• Cromwell, P. (1997). Poliedros . Reino Unido: Cambridge. pp. 79–86. Sólidos arquimedianos . ISBN . 0-521-55432-2.
• Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño . Dover Publications, Inc. ISBN 0-486-23729-X.
• Cromwell, P.; Poliedros, CUP hbk (1997), pbk. (1999).
• Weisstein, Eric W. , "Gran Rombicosidodecaedro" ("Sólido arquimediano") en MathWorld .
• Klitzing, Richard. "Poliedros uniformes convexos 3D x3x5x - cuadrícula".

• Weisstein, Eric W. "Gran rombicosidodecaedro". MathWorld .
• * Weisstein, Eric W. "Gran gráfico rombicosidodecaédrico". MathWorld .
• Red editable e imprimible de un icosidodecaedro truncado con vista 3D interactiva
• Los poliedros uniformes
• Poliedros de realidad virtual La enciclopedia de poliedros