8 cubos
Octeract de 8 cubos | |
|---|---|
 Proyección ortogonal dentro del polígono de Petrie | |
| Tipo | Politopo 8 regular |
| Familia | hipercubo |
| Símbolo de Schläfli | {4,3 6 } |
| Diagramas de Coxeter-Dynkin |               
|
| 7 caras | 16 {4,3 5 } |
| 6 caras | 112 {4,3 4 } |
| 5 caras | 448 {4,3 3 } |
| 4 caras | 1120 {4,3 2 } |
| Células | 1792 {4,3} |
| Caras | 1792 {4} |
| Bordes | 1024 |
| Vértices | 256 |
| Figura de vértice | 7-símplex  |
| Polígono de Petrie | hexadecágono |
| Grupo Coxeter | C 8 , [3 6 ,4] |
| Dual | 8-ortoplex  |
| Propiedades | convexo , politopo de Hanner |
En geometría , un 8-cubo es un hipercubo de ocho dimensiones . Tiene 256 vértices , 1024 aristas , 1792 caras cuadradas , 1792 celdas cúbicas , 1120 teseractos de 4 caras , 448 5-cubos de 5 caras , 112 6-cubos de 6 caras y 16 7-cubos de 7 caras .
Se representa con el símbolo de Schläfli {4,3 6 }, estando compuesto por 3 cubos de 7 dimensiones alrededor de cada cara de 6. Se le llama octeract , un acrónimo de tesseract (el cubo de 4 dimensiones ) y oct por ocho (dimensiones) en griego . También se le puede llamar hexdeca-8-topo regular o hexadecazetton , siendo un politopo de 8 dimensiones construido a partir de 16 facetas regulares .
Forma parte de una familia infinita de politopos, llamados hipercubos . El dual de un 8-cubo puede llamarse 8-ortoplex y forma parte de la familia infinita de politopos cruzados .
Coordenadas cartesianas
Las coordenadas cartesianas para los vértices de un cubo de 8 centrado en el origen y con una longitud de arista de 2 son
- (±1,±1,±1,±1,±1,±1,±1,±1)
mientras que el interior del mismo consta de todos los puntos (x 0 , x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 ) con -1 < x i < 1.
Como configuración
Esta matriz de configuración representa el cubo de 8 caras. Las filas y columnas corresponden a vértices, aristas, caras, celdas, 4 caras, 5 caras, 6 caras y 7 caras. Los números diagonales indican cuántos elementos de cada tipo hay en el cubo de 8 caras. Los números no diagonales indican cuántos elementos de la columna hay en el elemento de la fila o en él. [1] [2]
Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. [3]
| B8 |                | cara k | por favor | o0 | el 1 | el 2 | F3 | F4 | 5 | 6 | 7 | k -figura | notas |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Un 7 |                | ( ) | o0 | 256 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | {3,3,3,3,3,3} | B8 /A7 = 2^8* 8 !/8! = 256 |
| Un 6 Un 1 |                | { } | el 1 | 2 | 1024 | 7 | 21 | 35 | 35 | 21 | 7 | {3,3,3,3,3} | B8 / A6A1 = 2^ 8 * 8 !/ 7 !/2 = 1024 |
| Un 5 B 2 |                | {4} | el 2 | 4 | 4 | 1792 | 6 | 15 | 20 | 15 | 6 | {3,3,3,3} | B8 / A5B2 = 2 ^ 8 *8!/6!/4/2 = 1792 |
| Un 4 B 3 |                | {4,3} | F3 | 8 | 12 | 6 | 1792 | 5 | 10 | 10 | 5 | {3,3,3} | B8 /A4B3 = 2^ 8 * 8 !/5!/8/3 ! = 1792 |
| Un 3 B 4 |                | {4,3,3} | F4 | 16 | 32 | 24 | 8 | 1120 | 4 | 6 | 4 | {3,3} | B8 /A3B4 = 2^8*8!/4!/2^4/4 ! = 1120 |
| Un 2 B 5 |                | {4,3,3,3} | 5 | 32 | 80 | 80 | 40 | 10 | 448 | 3 | 3 | {3} | B8 / A2B5 = 2^8*8!/3!/2^5/5 ! = 448 |
| Un 1 B 6 |                | {4,3,3,3,3} | 6 | 64 | 192 | 240 | 160 | 60 | 12 | 112 | 2 | { } | B8 /A1B6 = 2^8*8!/2/2^6/6 ! = 112 |
| B7 |                | {4,3,3,3,3,3} | 7 | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 16 | ( ) | B8 / B7 = 2^8*8!/2^7/7! = 16 |
Proyecciones
 Este gráfico de 8 cubos es una proyección ortogonal . Esta orientación muestra columnas de vértices ubicados a una distancia vértice-arista-vértice desde un vértice de la izquierda hasta un vértice de la derecha, y aristas que unen columnas adyacentes de vértices. La cantidad de vértices en cada columna representa las filas del triángulo de Pascal , siendo 1:8:28:56:70:56:28:8:1. |
| B8 | B7 | ||||
|---|---|---|---|---|---|
 |  | ||||
| [16] | [14] | ||||
| B6 | B 5 | ||||
 |  | ||||
| [12] | [10] | ||||
| B4 | B3 | B2 | |||
 |  |  | |||
| [8] | [6] | [4] | |||
| Un 7 | Un 5 | Un 3 | |||
 | 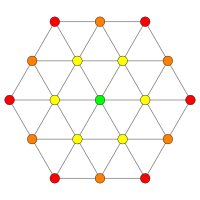 | 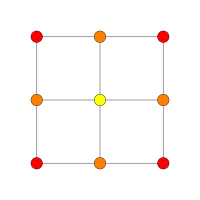 | |||
| [8] | [6] | [4] | |||
Politopos derivados
Aplicando una operación de alternancia , eliminando vértices alternos del octeracto, se crea otro politopo uniforme , llamado 8-demicubo , (parte de una familia infinita llamada demihipercubos ), que tiene 16 facetas demihepterácticas y 128 facetas 8-símplex.
Politopos relacionados
El 8-cubo es el octavo de una serie infinita de hipercubos :
 |  |  |  |  |  |  |  |  |  |
| Segmento de línea | Cuadrado | Cubo | 4 cubos | 5 cubos | 6 cubos | 7 cubos | 8 cubos | 9 cubos | 10 cubos |
Referencias
- ^ Coxeter, Politopos regulares, sección 1.8 Configuraciones
- ^ Coxeter, Politopos regulares complejos, p.117
- ^ Klitzing, Richard. "o3o3o3o3o3o3o4x - octubre".
- HSM Coxeter :
- Coxeter, Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN 0-486-61480-8 , pág. 296, Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
- (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
- Manuscrito de politopos uniformes de Norman Johnson (1991)
- NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. (1966)
- Klitzing, Richard. "Politopos uniformes 8D (polyzetta) o3o3o3o3o3o3o4x - octo".
Enlaces externos
- Weisstein, Eric W. "Hipercubo". MathWorld .
- Olshevsky, George. «Medición de politopos». Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
- Glosario multidimensional: hipercubo Garrett Jones

