Figura isoédrica

En geometría , una teselación de dimensión 2 (un mosaico plano) o superior, o un politopo de dimensión 3 (un poliedro ) o superior, es isoédrica o transitiva de caras si todas sus caras son iguales. Más específicamente, todas las caras no deben ser simplemente congruentes sino que deben ser transitivas , es decir, deben estar dentro de la misma órbita de simetría . En otras palabras, para dos caras cualesquiera A y B , debe haber una simetría de toda la figura por traslaciones , rotaciones y/o reflexiones que mapee A sobre B. Por esta razón, los poliedros isoédricos convexos son las formas que harán que los dados sean justos . [1]
Los poliedros isoédricos se denominan isoedros y pueden describirse por la configuración de sus caras . Un isoedro tiene un número par de caras.
El dual de un poliedro isoédrico es transitivo por vértice , es decir, isogonal. Los sólidos de Catalan , las bipirámides y los trapezoedros son todos isoédricos. Son los duales de los sólidos arquimedianos (isogonales) , prismas y antiprismas , respectivamente. Los sólidos platónicos , que son autoduales o duales con otro sólido platónico, son transitivos por vértice, arista y cara (es decir, isogonales, isotoxales e isoédricos).
Se dice que una forma que es isoédrica, tiene vértices regulares y también es transitiva en sus aristas (es decir, isotoxal) es un dual cuasirregular . Algunos teóricos consideran que estas figuras son verdaderamente cuasirregulares porque comparten las mismas simetrías, pero esto no es algo que se acepte en general.
Un poliedro que es isoédrico e isogonal se dice que es noble .
No todos los isozenoedros [2] son isoédricos. [3] Por ejemplo, un icosaedro rómbico es un isozenoedro pero no un isoedro. [4]
Ejemplos
| Convexo | Cóncavo | ||
|---|---|---|---|
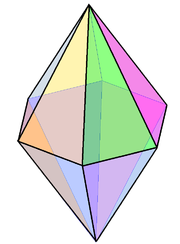 Las bipirámides hexagonales , V4.4.6, son poliedros isoédricos no regulares . |  El mosaico pentagonal de El Cairo , V3.3.4.3.4, es isoédrico. |  El panal dodecaédrico rómbico es isoédrico (e isocórico y ocupa todo el espacio). |  Una teselación cuadrada distorsionada en una teselación H en espiral (topológicamente equivalente) sigue siendo isoédrica. |
Clases de isoedros por simetría
| Caras | Configuración de cara . | Clase | Nombre | Simetría | Orden | Convexo | Coplanar | No convexo |
|---|---|---|---|---|---|---|---|---|
| 4 | V3 3 | platónico | tetraedro difenoide tetragonal difenoide rómbico | T d , [3,3], (*332) D 2d , [2 + ,2], (2*) D 2 , [2,2] + , (222) | 24 4 4 4 |    | ||
| 6 | Versión 3 4 | platónico | cubo trapezoedro trigonal trapezoedro trigonal asimétrico | Oh , [4,3], (*432) D 3d , [2 + , 6 ] (2*3) D 3 [2,3] + , (223) | 48 12 12 6 |    | ||
| 8 | V4 3 | platónico | octaedro bipirámide cuadrada bipirámide rómbica escalenoedro cuadrado | Oh , [4,3], (*432) D 4h , [2,4], (*224) D 2h , [2,2], (*222) D 2d , [2 + , 4], (2*2) | 48 16 8 8 |   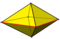    |  | |
| 12 | V3 5 | platónico | dodecaedro regular piritoedro tetartoide | Yo , [5,3], (*532) T , [3 + , 4], (3*2) T, [3,3] + , (*332) | 120 24 12 |   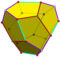 | 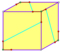 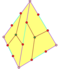 |   |
| 20 | V5 3 | platónico | icosaedro regular | Yo soy , [5,3], (*532) | 120 |  | ||
| 12 | Versión 3.6 2 | catalán | triakis tetraedro | T d , [3,3], (*332) | 24 |  |   |  |
| 12 | V(3.4) 2 | catalán | dodecaedro rómbico dodecaedro deltoidal | O h , [4,3], (*432) T d , [3,3], (*332) | 48 24 |    |  |   |
| 24 | Versión 3.8 2 | catalán | triakis octaedro | Oh , [4,3], (*432 ) | 48 |  |   | |
| 24 | Versión 4.6 2 | catalán | tetrakis hexaedro | Oh , [4,3], (*432 ) | 48 |   |   |   |
| 24 | Versión 3.4 3 | catalán | icositetraedro deltoidal | Oh , [4,3], (*432 ) | 48 |  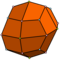 |    |  |
| 48 | V4.6.8 | catalán | Dodecaedro de Disdyakis | Oh , [4,3], (*432 ) | 48 |  |    |   |
| 24 | Versión 3 4 .4 | catalán | icositetraedro pentagonal | O, [4,3] + , (432) | 24 |  | ||
| 30 | V(3,5) 2 | catalán | triacontaedro rómbico | Yo soy , [5,3], (*532) | 120 |  | ||
| 60 | V3.10 2 | catalán | triakisicosaedro | Yo soy , [5,3], (*532) | 120 |  |     | |
| 60 | Versión 5.6 2 | catalán | Dodecaedro pentakis | Yo soy , [5,3], (*532) | 120 |  |      | |
| 60 | V3.4.5.4 | catalán | hexecontaedro deltoidal | Yo soy , [5,3], (*532) | 120 |  |  |  |
| 120 | V4.6.10 | catalán | Triacontaedro de Disdyakis | Yo soy , [5,3], (*532) | 120 |  |    |    |
| 60 | Versión 3 4.5 | catalán | hexecontaedro pentagonal | Yo, [5,3] + , (532) | 60 |  | ||
| 2 n | V3 3 . n | Polar | trapezoedro trapezoedro asimétrico | D n d , [2 + ,2 n ], (2* n ) D n , [2, n ] + , (22 n ) | 4 y 2 y |   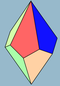    | ||
| 2 y 4 y | V4 2 . n V4 2 .2 n V4 2 .2 n | Polar | n - bipirámide regular isotoxal 2 n -bipirámide 2 n - escalenoedro | D n h , [2, n ], (*22 n ) D n h , [2, n ], (*22 n ) D n d , [2 + ,2 n ], (2* n ) | 4 n | 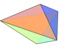    |        |
a-isoédricocifra
Un poliedro (o politopo en general) es k -isoédrico si contiene k caras dentro de sus dominios fundamentales de simetría. [5] De manera similar, un mosaico k -isoédrico tiene k órbitas de simetría separadas (puede contener m formas de caras diferentes, para m = k , o solo para algunas m < k ). [6] ("1-isoédrico" es lo mismo que "isoédrico").
Un poliedro monoédrico o teselación monoédrica ( m = 1) tiene caras congruentes, ya sea directa o reflexivamente, que se presentan en una o más posiciones de simetría. Un poliedro o teselación m -édrica tiene m formas de cara diferentes (" diédrico ", " triédrico "... son lo mismo que "2-édrico", "3-édrico"... respectivamente). [7]
A continuación se muestran algunos ejemplos de poliedros y teselaciones k -isoédricas, con sus caras coloreadas según sus posiciones de simetría k :
| 3-isoédrico | 4-isoédrico | isoédrica | 2-isoédrico |
|---|---|---|---|
| Poliedros de caras regulares de 2 hedrales | Poliedros monoédricos | ||
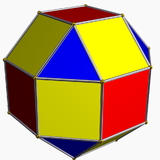 | 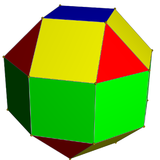 | 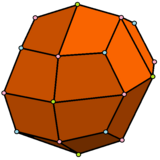 | 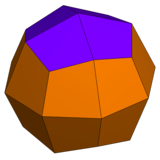 |
| El rombicuboctaedro tiene 1 tipo de triángulo y 2 tipos de cuadrado. | El pseudo-rombicuboctaedro tiene 1 tipo de triángulo y 3 tipos de cuadrado. | El icositetraedro deltoidal tiene 1 tipo de cara. | El icositetraedro pseudodeltoidal tiene 2 tipos de caras, con la misma forma. |
| 2-isoédrico | 4-isoédrico | Isoédrica | 3-isoédrico |
|---|---|---|---|
| Teselas de caras regulares de 2 hedrales | Teselación monoédrica | ||
 |  |  |  |
| El mosaico pitagórico tiene 2 tipos de cuadrados (tamaños). | Este mosaico de 3 uniformes tiene 3 tipos de triángulos, con la misma forma, y 1 tipo cuadrado. | El patrón de espiga tiene 1 tipo de rectángulo. | Este mosaico pentagonal tiene 3 tipos de pentágonos irregulares, con la misma forma. |
Términos relacionados
Una figura transitiva de celdas o isocórica es un politopo n ( n ≥ 4) o un panal n ( n ≥ 3) que tiene sus celdas congruentes y transitivas entre sí. En 3 dimensiones, los panales catóptricos , duales de los panales uniformes, son isocóricos. En 4 dimensiones, se han enumerado politopos isocóricos de hasta 20 celdas. [8]
Una figura isotópica o transitiva por facetas es un politopo o panal de abeja de n dimensiones con sus facetas (( n −1)- caras ) congruentes y transitivas. El dual de un isótopo es un politopo isogonal . Por definición, esta propiedad isotópica es común a los duales de los politopos uniformes .
- Una figura isotópica bidimensional es isotoxal, es decir, transitiva en cuanto a los bordes.
- Una figura tridimensional isotópica es isoédrica, es decir, transitiva en sus caras.
- Una figura isotópica de 4 dimensiones es isocórica, es decir, transitiva a nivel celular.
Véase también
Referencias
- ^ McLean, K. Robin (1990), "Mazmorras, dragones y dados", The Mathematical Gazette , 74 (469): 243–256, doi :10.2307/3619822, JSTOR 3619822, S2CID 195047512.
- ^ Weisstein, Eric W. "Isozonohedron". mathworld.wolfram.com . Consultado el 26 de diciembre de 2019 .
- ^ Weisstein, Eric W. "Isoedro". mathworld.wolfram.com . Consultado el 21 de diciembre de 2019 .
- ^ Weisstein, Eric W. "Icosaedro rómbico". mathworld.wolfram.com . Consultado el 21 de diciembre de 2019 .
- ^ Socolar, Joshua ES (2007). "Azulejos de parquet hexagonales: monoazulejos k-isoédricos con k arbitrariamente grande" (PDF corregido) . The Mathematical Intelligencer . 29 (2): 33–38. arXiv : 0708.2663 . doi :10.1007/bf02986203. S2CID 119365079. Consultado el 9 de septiembre de 2007 .
- ^ Craig S. Kaplan, "Introducción a la teoría de mosaicos para gráficos por computadora", archivado el 8 de diciembre de 2022 en Wayback Machine , 2009, capítulo 5: "Mosaicos isoédricos", pág. 35.
- ^ Azulejos y patrones , pág. 20, 23.
- ^ "Dados de cuatro dimensiones hasta veinte caras".
Enlaces externos
- Olshevsky, George. "Isótopo". Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
- Weisstein, Eric W. "Teselación isoédrica". MathWorld .
- Weisstein, Eric W. "Isoedro". MathWorld .
- isoedros 25 clases de isoedros con un número finito de lados
- Diseño de dados en The Dice Lab