6-demicubes
Politopo uniforme de 6 elementos
Demihexeract
(6 demicubo)

Proyección del polígono de Petrie
TipoPolitopo uniforme de 6 elementos
Familiasemihipercubo
Símbolo de Schläfli{3,3 3,1 } = h{4,3 4 }
s{2 1,1,1,1,1 }
Diagramas de Coxeter=
=





Símbolo de Coxeter1 31
5 caras4412  {3 1,2,1 }
32 {3 4 }
4 caras25260 {3 1,1,1 }
192 {3 3 }
Células640160 {3 1,0,1 }
480 {3,3}
Caras640{3}
Bordes240
Vértices32
Figura de vérticeRectificado 5-simplex
Grupo de simetríaD 6 , [3 3,1,1 ] = [1 + ,4,3 4 ]
[2 5 ] +
Polígono de Petriedecágono
Propiedadesconvexo

En geometría , un 6-demicube o semihexeracto es un 6-politopo uniforme , construido a partir de un 6-cubo ( hexeracto ) al que se le han quitado los vértices alternados . Forma parte de una familia dimensionalmente infinita de politopos uniformes llamados semihipercubos .

EL Elte lo identificó en 1912 como un politopo semirregular, etiquetándolo como HM 6 para un politopo de media medida de 6 dimensiones .

Coxeter nombró a este politopo como 1 31 a partir de su diagrama de Coxeter , con un anillo en una de las ramas de 1 longitud,Se puede nombrar de manera similar mediante un símbolo de Schläfli exponencial tridimensional o {3,3 3,1 }. { 3 3 , 3 , 3 3 } {\displaystyle \left\{3{\begin{array}{l}3,3,3\\3\end{array}}\right\}}

Coordenadas cartesianas

Las coordenadas cartesianas de los vértices de un semihexerato centrado en el origen son mitades alternas del hexerato :

(±1,±1,±1,±1,±1,±1)

con un número impar de signos más.

Como configuración

Esta matriz de configuración representa el semicubeo de 6 caras. Las filas y columnas corresponden a vértices, aristas, caras, celdas, caras de 4 y caras de 5 caras. Los números diagonales indican cuántos elementos de cada tipo se encuentran en el semicubeo de 6 caras. Los números no diagonales indican cuántos elementos de la columna se encuentran en el elemento de la fila o en su interior. [1] [2]

Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. [3]

D6​cara kpor favoro0​el 1el 2F3​F4​5​k -figuranotas
Un 4( )o0​3215602060153066r{3,3,3,3}D6 /A4 = 32* 6 !/5! = 32
Un 3 Un 1 Un 1{ }el 1224084126842{}x{3,3}D6 / A3A1A1 = 32 * 6 !/4!/2/ 2 = 240
Un 3 Un 2{3}el 233640133331{3}v( )D6 / A3A2 = 32 * 6 !/ 4 !/3! = 640
Un 3 Un 1h{4,3}F3​464160*3030{3}D6 / A3A1 = 32 * 6 !/4!/2 = 160
Un 3 Un 2{3,3}464*4801221{}v( )D6 / A3A2 = 32 * 6 !/4!/3! = 480
D4A1​​​h{4,3,3}F4​824328860*20{ }D6 / D4A1 = 32 * 6 !/ 8 /4!/2 = 60
Un 4{3,3,3}5101005*19211D6 /A4 = 32* 6 !/5! = 192
D 5h{4,3,3,3}5​16801604080101612*( )D6 /D5 = 32* 6 !/16/5! = 12
Un 5{3,3,3,3}6152001506*32D6 /A5 = 32* 6 !/6! = 32

Imágenes

proyecciones ortográficas
Avión CoxeterB6​
Gráfico
Simetría diedral[12/2]
Avión CoxeterD6​D 5
Gráfico
Simetría diedral[10][8]
Avión CoxeterD4​D3​
Gráfico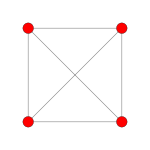
Simetría diedral[6][4]
Avión CoxeterUn 5Un 3
Gráfico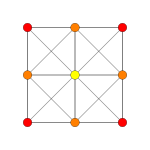
Simetría diedral[6][4]

Hay 47 politopos uniformes con simetría D 6 , 31 son compartidos por la simetría B 6 y 16 son únicos:

Politopos D6

h{4,34}
h2 { 4,3 4 }
h3 { 4,3 4 }
h4 { 4,34 }​
h5 { 4,3 4 }
h2,3 { 4,3 4 }
h2,4 { 4,3 4 }
h2,5 { 4,3 4 }

h3,4 { 4,3 4 }
h3,5 { 4,3 4 }
h4,5 { 4,3 4 }
h2,3,4 { 4,3 4 }
h2,3,5 { 4,3 4 }
h2,4,5 { 4,3 4 }
h3,4,5 { 4,3 4 }
2,3,4,5 { 4,3 4 }

El 6-demicubo, 1 31 es el tercero en una serie dimensional de politopos uniformes, expresado por Coxeter como la serie k 31 . La quinta figura es un panal euclidiano, 3 31 , y la última es un panal hiperbólico no compacto, 4 31 . Cada politopo uniforme progresivo se construye a partir del anterior como su figura de vértice .

k 31 figuras dimensionales
norte456789

Grupo Coxeter		Un 3 Un 1Un 5D6​E7​ mi ~ 7 {\displaystyle {\tilde {E}}_{7}} = E7 + yo ¯ 8 {\displaystyle {\bar {T}}_{8}} = E7 ++

Diagrama de Coxeter
Simetría[3 −1,3,1 ][3 0,3,1 ][3 1,3,1 ][3 2,3,1 ][3 3,3,1 ][3 4,3,1 ]
Orden4872023.0402.903.040∞
Gráfico--
Nombre-1 310 311312 313 314 31

También es la segunda de una serie dimensional de politopos y panales uniformes, expresada por Coxeter como la serie 1 3k . La cuarta figura es el panal euclidiano 1 33 y la última es un panal hiperbólico no compacto, 1 34 .

1 figuras dimensionales de 3k
EspacioFinitoEuclidianoHiperbólico
norte456789

Grupo Coxeter		Un 3 Un 1Un 5D6​E7​ mi ~ 7 {\displaystyle {\tilde {E}}_{7}} =E 7 + yo ¯ 8 {\displaystyle {\bar {T}}_{8}} = E7 ++

Diagrama de Coxeter
Simetría[3 −1,3,1 ][3 0,3,1 ][3 1,3,1 ][3 2,3,1 ][[3 3,3,1 ]][3 4,3,1 ]
Orden4872023.0402.903.040∞
Gráfico--
Nombre1 3,-11 301311 321 33134

Icosaedro oblicuo

Coxeter identificó un subconjunto de 12 vértices que forman un icosaedro oblicuo regular {3, 5} con las mismas simetrías que el propio icosaedro, pero en ángulos diferentes. Lo denominó icosaedro oblicuo regular . [4] [5]

Referencias

  1. ^ Coxeter, Politopos regulares, sección 1.8 Configuraciones
  2. ^ Coxeter, Politopos regulares complejos, p.117
  3. ^ Klitzing, Richard. "x3o3o *b3o3o3o - hax".
  4. ^ Coxeter, HSM La belleza de la geometría: doce ensayos (edición Dover). Dover Publications. págs. 450–451. ISBN 9780486409191.
  5. ^ Deza, Michael; Shtogrin, Mikhael (2000). "Incorporación de los gráficos de teselas regulares y panales de abejas en los gráficos de hipercubos y redes cúbicas". Estudios avanzados en matemáticas puras : 77. doi : 10.2969/aspm/02710073 . Consultado el 4 de abril de 2020 .
  • HSM Coxeter :
    • Coxeter, Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN 0-486-61480-8 , pág. 296, Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5) 
    • HSM Coxeter, Regular Polytopes , 3.ª edición, Dover Nueva York, 1973, pág. 296, Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)
    • Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
      • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
      • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
      • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
  • John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26, págs. 409: Hemicubos: 1 n1 ) 
  • Klitzing, Richard. "Polipetas uniformes 6D x3o3o *b3o3o3o – hax".
  • Olshevsky, George. "Demihexeract". Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
  • Glosario multidimensional
Politopos fundamentales convexos regulares y uniformes en dimensiones 2–10
FamiliaUn​Bn​Yo 2 (p) / D nMi 6 / Mi 7 / Mi 8 / Fa 4 / Sol 2H- n
Polígono regularTriánguloCuadradop-gonHexágonoPentágono
Poliedro uniformeTetraedroOctaedro • CuboSemicuboDodecaedro • Icosaedro
Policoron uniformePentachoron16 celdas • TesseractActo de Demitesseract24 celdas120 celdas • 600 celdas
Politopo 5 uniforme5-símplex5-ortoplex • 5-cubo5-demicubes
Politopo uniforme de 6 elementos6-símplex6-ortoplex • 6-cubo6-demicubes1 22 • 2 21
Politopo 7 uniforme7-símplex7-ortoplex • 7-cubo7-demicube1 32 • 2 31 • 3 21
Politopo 8 uniforme8-símplex8-ortoplex • 8-cubo8-demicubes1 42 • 2 41 • 4 21
Politopo uniforme de 9 elementos9-símplex9-ortoplex • 9-cubo9-demicubes
Politopo uniforme de 1010-símplex10-ortoplex • 10-cubo10-demicubes
Politopo uniforme n​n - símplexn - ortoplex • n - cubon - demicubo1 k2 • 2 k1 • k21​n - politopo pentagonal
Temas: Familias de politopos • Politopo regular • Lista de politopos regulares y compuestos
Obtenido de "https://es.wikipedia.org/w/index.php?title=6-demicube&oldid=1218086694"