Diagrama de Coxeter-Dynkin
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|


En geometría , un diagrama de Coxeter - Dynkin (o diagrama de Coxeter , gráfico de Coxeter ) es un gráfico con aristas etiquetadas numéricamente (llamadas ramas ) que representan un grupo de Coxeter o, a veces, un politopo uniforme o un teselado uniforme construido a partir del grupo.
Una clase de objetos estrechamente relacionados son los diagramas de Dynkin , que difieren de los diagramas de Coxeter en dos aspectos: en primer lugar, las ramas etiquetadas como " 4 " o mayores son dirigidas , mientras que los diagramas de Coxeter no son dirigidas ; en segundo lugar, los diagramas de Dynkin deben satisfacer una restricción ( cristalográfica ) adicional, a saber, que las únicas etiquetas de rama permitidas son 2, 3, 4 y 6. Los diagramas de Dynkin corresponden y se utilizan para clasificar sistemas de raíces y, por lo tanto, álgebras de Lie semisimples . [1]
Descripción
Un grupo de Coxeter es un grupo que admite una presentación: donde los m i,j son los elementos de alguna matriz simétrica M que tiene 1 s en su diagonal . [a] Esta matriz M , la matriz de Coxeter , determina completamente el grupo de Coxeter.
Como la matriz de Coxeter es simétrica, se la puede considerar como la matriz de adyacencia de un grafo con aristas etiquetadas que tiene vértices correspondientes a los generadores r i y aristas etiquetadas con m i,j entre los vértices correspondientes a r i y r j . Para simplificar estos diagramas, se pueden realizar dos cambios:
- Los bordes que están etiquetados con 2 se pueden omitir, y se supone que los bordes faltantes son 2 s. Una etiqueta 2 indica que los dos generadores correspondientes conmutan; 2 es el número más pequeño que se puede usar para etiquetar un borde.
- Los bordes etiquetados como 3 se pueden dejar sin etiquetar, con la implicación de que un borde sin etiqueta actúa como un 3 .
El gráfico resultante es un diagrama de Coxeter-Dynkin que describe el grupo de Coxeter considerado.
Matriz de Schläfli
Cada diagrama de Coxeter tiene una matriz de Schläfli correspondiente (llamada así por Ludwig Schläfli ), A , con elementos de matriz a i,j = a j,i = −2 cos( π / p i,j ) donde p i,j es el orden de ramificación entre los espejos i y j ; es decir, π / p i,j es el ángulo diedro entre los espejos i y j . Como matriz de cosenos , A también se llama matriz de Gram . Todas las matrices de Schläfli del grupo de Coxeter son simétricas porque sus vectores raíz están normalizados. A está estrechamente relacionada con la matriz de Cartan , utilizada en el grafo similar pero dirigido: el diagrama de Dynkin , en los casos limitados de p = 2, 3, 4 y 6, que generalmente no son simétricos.
El determinante de la matriz de Schläfli se llama Schläfliano ; [ cita requerida ] el Schläfliano y su signo determinan si el grupo es finito (positivo), afín (cero) o indefinido (negativo). [2] Esta regla se llama Criterio de Schläfli . [3] [ verificación fallida ]
Los valores propios de la matriz de Schläfli determinan si un grupo de Coxeter es de tipo finito (todos positivos), de tipo afín (todos no negativos, al menos uno es cero) o de tipo indefinido (de lo contrario). El tipo indefinido a veces se subdivide, por ejemplo, en grupos hiperbólicos y otros grupos de Coxeter. Sin embargo, existen múltiples definiciones no equivalentes para los grupos hiperbólicos de Coxeter. Usamos las siguientes definiciones:
- Un grupo de Coxeter con diagrama conexo es hiperbólico si no es de tipo finito ni afín, pero todo subdiagrama conexo propio es de tipo finito o afín.
- Un grupo de Coxeter hiperbólico es compacto si todos sus subgrupos son finitos (es decir, tienen determinantes positivos), y paracompacto si todos sus subgrupos son finitos o afines (es decir, tienen determinantes no negativos).
Los grupos finitos y afines también se denominan elípticos y parabólicos respectivamente. Los grupos hiperbólicos también se denominan Lannér, en honor a F. Lannér, quien enumeró los grupos hiperbólicos compactos en 1950, [4] y Koszul (o cuasi-Lannér) para los grupos paracompactos.
Grupos de Coxeter de rango 2
El tipo de un grupo de Coxeter de rango 2 , es decir, generado por dos espejos diferentes, está completamente determinado por el determinante de la matriz de Schläfli, ya que este determinante es simplemente el producto de los valores propios: tipo finito (determinante positivo), afín (determinante cero) o hiperbólico (determinante negativo). Coxeter utiliza una notación de corchetes equivalente que enumera secuencias de órdenes de rama como sustituto de los diagramas gráficos de nodo-rama. Soluciones racionales [ p / q ], 



 , también existen, con mcd ( p , q ) = 1; estos definen dominios fundamentales superpuestos. Por ejemplo, 3/2, 4/3, 5/2, 5/3, 5/4 y 6/5.
, también existen, con mcd ( p , q ) = 1; estos definen dominios fundamentales superpuestos. Por ejemplo, 3/2, 4/3, 5/2, 5/3, 5/4 y 6/5.
| Tipo | Finito | Afín | Hiperbólico | |||||
|---|---|---|---|---|---|---|---|---|
| Geometría |  |  |  |  | ... |  |  |  |
| Diagrama de Coxeter Notación entre corchetes |  [ ] |    [2] |    [3] |    [4] |    [ pag ] |    [∞] |    [∞] |    [iπ/ λ ] |
| Orden | 2 | 4 | 6 | 8 | 2 p | ∞ | ||
| Las líneas reflejadas están coloreadas para corresponderse con los nodos del diagrama de Coxeter. Los dominios fundamentales están coloreados de forma alternada. | ||||||||
| Diagramas de grupo de Coxeter de rango 2 | |||||||
|---|---|---|---|---|---|---|---|
| Orden p | Grupo | Diagrama de Coxeter | Matriz de Schläfli | ||||
| Determinante | |||||||
| Finito (Determinante > 0) | |||||||
| 2 | Yo 2 (2) = A 1 × A 1 |    | [2] | 4 | |||
| 3 | Yo 2 (3) = A 2 |    | [3] | 3 | |||
| 3/2 |      | [3/2] | |||||
| 4 | Yo 2 (4) = B 2 |    | [4] | 2 | |||
| 4/3 |      | [4/3] | |||||
| 5 | Yo 2 (5) = H 2 |    | [5] | ≈ 1,38196601125 | |||
| 5/4 |      | [5/4] | |||||
| 5/2 |    | [5/2] | ≈ 3,61803398875 | ||||
| 5/3 |  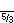  | [5/3] | |||||
| 6 | Yo 2 (6) = G 2 |    | [6] | 1 | |||
| 6/5 |      | [6/5] | |||||
| 8 | Yo 2 (8) |    | [8] | ≈ 0,58578643763 | |||
| 10 | Yo 2 (10) |    | [10] | ≈ 0,38196601125 | |||
| 12 | Yo 2 (12) |    | [12] | ≈ 0,26794919243 | |||
| pag | Yo 2 ( pág ) |    | [ pag ] | ||||
| Afín (Determinante = 0) | |||||||
| ∞ | Yo 2 (∞) = = |    | [∞] | 0 | |||
| Hiperbólico (Determinante ≤ 0) | |||||||
| ∞ |    | [∞] | 0 | ||||
| ∞ |    | [iπ/ λ ] | |||||
Visualizaciones geométricas
El diagrama de Coxeter-Dynkin puede considerarse una descripción gráfica del dominio fundamental de los espejos. Un espejo representa un hiperplano dentro de un espacio esférico, euclidiano o hiperbólico de una dimensión determinada. (En espacios 2D, un espejo es una línea; en 3D, un espejo es un plano).
Estas visualizaciones muestran los dominios fundamentales para los grupos euclidianos 2D y 3D, y para los grupos esféricos 2D. Para cada uno, el diagrama de Coxeter se puede deducir identificando los espejos hiperplanos y etiquetando su conectividad, ignorando los ángulos diedros de 90 grados (orden 2; ver nota al pie [a] a continuación).
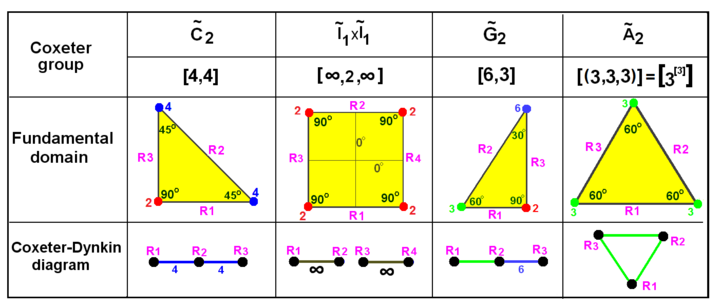 Grupos de Coxeter en el plano euclidiano con diagramas equivalentes. Aquí, los vértices del dominio se etiquetan como ramas del grafo 1, 2, etc., y se colorean según su orden de reflexión (conectividad). Las reflexiones se etiquetan como nodos del grafo R1, R2, etc. Las reflexiones a 90 grados están inactivas en el sentido de que, juntas, no generan nuevas reflexiones; [b] por lo tanto, no están conectadas entre sí por una rama en el diagrama. Los espejos paralelos están conectados entre sí por una rama etiquetada con ∞ . El cuadrado del grupo prismático × se muestra como una duplicación del triángulo alrededor de su lado R2 *, pero también se puede crear como un dominio rectangular a partir de la duplicación del triángulo alrededor de su lado R2 *. El triángulo es una duplicación del triángulo alrededor de su lado R3 *. *(este lado desaparece al duplicarse alrededor de sí mismo) | |
 Muchos grupos de Coxeter en el plano hiperbólico pueden extenderse a partir de los casos euclidianos como una serie de soluciones hiperbólicas. | |
 Grupos de Coxeter en el espacio tridimensional con diagramas. Los espejos (caras de triángulos) están etiquetados por vértice opuesto: 0, ..., 3. Las ramas están coloreadas según su orden de reflexión. llena 1/48 del cubo. llena 1/24 del cubo. llena 1/12 del cubo. |  Grupos de Coxeter en la esfera con diagramas equivalentes. Un dominio fundamental está delineado en amarillo. Los vértices del dominio (y las ramas del grafo) están coloreados según su orden de reflexión. |
Aplicación a politopos uniformes
 Al construir politopos uniformes, los nodos se marcan como activos mediante un anillo si un punto generador está fuera del espejo, lo que crea un nuevo borde entre un punto generador y su imagen reflejada. Un nodo sin anillo representa un espejo inactivo que no genera puntos nuevos. Un anillo sin nodo se denomina agujero . | 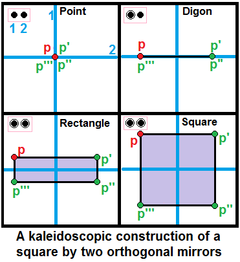 Se pueden utilizar dos espejos ortogonales para generar un cuadrado,    , que se ve aquí con un punto generador rojo y tres copias virtuales en los espejos. El generador tiene que estar fuera de ambos espejos en este caso ortogonal para generar un interior. El marcado de anillos supone que los anillos activos tienen generadores a la misma distancia de todos los espejos, mientras que un rectángulo también puede representar una solución no uniforme. , que se ve aquí con un punto generador rojo y tres copias virtuales en los espejos. El generador tiene que estar fuera de ambos espejos en este caso ortogonal para generar un interior. El marcado de anillos supone que los anillos activos tienen generadores a la misma distancia de todos los espejos, mientras que un rectángulo también puede representar una solución no uniforme. |
Los diagramas de Coxeter-Dynkin pueden enumerar explícitamente casi todas las clases de politopo uniforme y teselaciones uniformes . Cada politopo uniforme con simetría reflexiva pura (todos, salvo unos pocos casos especiales, tienen simetría reflexiva pura) se puede representar mediante un diagrama de Coxeter-Dynkin con permutaciones de marcas . Cada politopo uniforme se puede generar utilizando dichos espejos y un único punto generador: las imágenes especulares crean nuevos puntos como reflejos, luego se pueden definir los bordes del politopo entre los puntos y un punto de imagen especular. Las caras se generan por la reflexión repetida de un borde que eventualmente envuelve al generador original; la forma final, así como cualquier faceta de dimensión superior, también se crean mediante la cara que se refleja para encerrar un área.
Para especificar el vértice generador, uno o más nodos se marcan con anillos, lo que significa que el vértice no está en el espejo o espejos representados por el nodo o los nodos con anillos. (Si se marcan dos o más espejos, el vértice es equidistante de ellos). Un espejo está activo (crea reflejos) solo con respecto a los puntos que no están en él. Un diagrama necesita al menos un nodo activo para representar un politopo. Un diagrama no conectado (subgrupos separados por ramas de orden 2 o espejos ortogonales) requiere al menos un nodo activo en cada subgrafo.
Todos los politopos regulares , representados por el símbolo de Schläfli { p , q , r , ...} , pueden tener sus dominios fundamentales representados por un conjunto de n espejos con un diagrama de Coxeter-Dynkin relacionado de una línea de nodos y ramas etiquetados por p , q , r , ..., con el primer nodo anillado.
Los politopos uniformes con un anillo corresponden a puntos generadores en las esquinas del dominio fundamental del símplex. Dos anillos corresponden a las aristas del símplex y tienen un grado de libertad, con solo el punto medio como solución uniforme para longitudes de aristas iguales. En general, los puntos generadores del anillo k están en las (k-1) caras del símplex, y si todos los nodos están anillados, el punto generador está en el interior del símplex.
El caso especial de politopos uniformes con simetría no reflexiva se representa mediante un marcado secundario en el que se elimina el punto central de un nodo anillado (lo que se denomina agujero ). Estas formas son alternancias de politopos con simetría reflexiva, lo que implica que se eliminan todos los demás vértices. El politopo resultante tendrá una subsimetría del grupo de Coxeter original . Una alternancia truncada se denomina snub .
- Un nodo único representa un espejo único. Esto se denomina grupo A 1 . Si se anilla, se crea un segmento de línea perpendicular al espejo, representado como {}.
- Dos nodos no unidos representan dos espejos perpendiculares . Si ambos nodos están rodeados por un anillo, se puede crear un rectángulo , o un cuadrado si el punto está a la misma distancia de ambos espejos.
- Dos nodos unidos por una rama de orden n pueden crear un n -gono si el punto está en un espejo, y un 2n - gono si el punto está fuera de ambos espejos. Esto forma el grupo I 1 (n) .
- Dos espejos paralelos pueden representar un grupo de polígonos infinitos I 1 (∞) , también llamado Ĩ 1 .
- Tres espejos en un triángulo forman imágenes que se ven en un caleidoscopio tradicional y se pueden representar mediante tres nodos conectados en un triángulo. Los ejemplos repetidos tendrán ramas etiquetadas como (3 3 3), (2 4 4), (2 3 6), aunque las dos últimas se pueden dibujar como una línea (sin tener en cuenta las dos ramas). Esto generará teselas uniformes .
- Tres espejos pueden generar poliedros uniformes ; incluyendo números racionales se obtiene el conjunto de triángulos de Schwarz .
- Tres espejos, uno perpendicular a los otros dos, pueden formar prismas uniformes .
 Hay 7 construcciones uniformes reflectantes dentro de un triángulo general, basadas en 7 posiciones de generador topológico dentro del dominio fundamental. Cada espejo activo genera un borde, con dos espejos activos que tienen generadores en los lados del dominio y tres espejos activos que tienen el generador en el interior. Se pueden resolver uno o dos grados de libertad para una posición única para longitudes de borde iguales del poliedro o mosaico resultante. |  Ejemplo 7 generadores sobre simetría octaédrica , dominio fundamental triángulo (4 3 2), con 8va generación de snub como alternancia |
Los duales de los politopos uniformes a veces se marcan con una barra perpendicular que reemplaza los nodos anillados y con un agujero en la barra para los nodos huecos de los romos. Por ejemplo,

 representa un rectángulo (como dos espejos ortogonales activos), y
representa un rectángulo (como dos espejos ortogonales activos), y

 representa su polígono dual , el rombo .
representa su polígono dual , el rombo .
Ejemplos con poliedros y teselaciones
Por ejemplo, el grupo B 3 de Coxeter tiene un diagrama:



 Esto también se llama simetría octaédrica .
Esto también se llama simetría octaédrica .
Hay 7 poliedros uniformes convexos que pueden construirse a partir de este grupo de simetría y 3 a partir de sus subsimetrías de alternancia , cada uno con un diagrama de Coxeter-Dynkin marcado de forma única. El símbolo de Wythoff representa un caso especial del diagrama de Coxeter para grafos de rango 3, con los 3 órdenes de ramificación nombrados, en lugar de suprimir las ramas de orden 2. El símbolo de Wythoff puede manejar la forma de snub , pero no las alternancias generales sin todos los nodos anillados.
| Poliedros octaédricos uniformes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetría : [4,3], (*432) | [4,3] + (432) | [1 + ,4,3] = [3,3] (*332) | [3 + ,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{3 1,1 } | t{3,4} t{3 1,1 } | {3,4} {3 1,1 } | rr { 4,3} s2 {3,4} | tr{4,3} | sr{4,3} | h{4,3} {3,3} | h2 {4,3} t { 3,3} | s{3,4} s{3 1,1 } |
     |      |      |      |      |      |      |      |      | ||
     =    |      =    |      =    |      |      = =   o o   |      = =   o o   |      = =   | ||||
 |  |   |   |   |   |  |  |   |   |   |
| De poliedros duales a uniformes | ||||||||||
| V4 3 | Versión 3.8 2 | V(3.4) 2 | Versión 4.6 2 | Versión 3 4 | Versión 3.4 3 | V4.6.8 | Versión 3 4 .4 | V3 3 | Versión 3.6 2 | V3 5 |
     |      |      |      |      |      |      |      |      |      |      |
     |      |      |      |      |      |      | ||||
 |  |  |  |  |  |  |  |  |  |  |
Las mismas construcciones se pueden realizar en grupos de Coxeter disjuntos (ortogonales) como los prismas uniformes , y se pueden ver más claramente como teselas de diedros y hosoedros en la esfera, como esta familia [6]×[] o [6,2]:
| Poliedros esféricos diedros hexagonales uniformes | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetría : [6,2] , (*622) | [6,2] + , (622) | [6,2 + ], (2*3) | ||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
     |      |      |      |      |      |      |      |      | ||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| De duales a uniformes | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
| V6 2 | V12 2 | V6 2 | V4.4.6 | Versión 2 6 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
En comparación, [6,3],



 La familia produce un conjunto paralelo de 7 teselación uniforme del plano euclidiano y sus teselación dual. Hay nuevamente 3 alternancias y alguna versión de semisimetría.
La familia produce un conjunto paralelo de 7 teselación uniforme del plano euclidiano y sus teselación dual. Hay nuevamente 3 alternancias y alguna versión de semisimetría.
| Teselación hexagonal/triangular uniforme | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetría : [6,3], (*632) | [6,3] + (632) | [6,3 + ] (3*3) | |||||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | s{3,6} | |||
     |      |      |      |      |      |      |      |      | |||
 |  |  |  |  |  |  |  |  | |||
| 6 3 | 3.12 2 | (3.6) 2 | 6.6.6 | 3 6 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Duelos uniformes | |||||||||||
 |  |  |  |  |  |  |  |  | |||
| V6 3 | Versión 3.12 2 | V(3.6) 2 | V6 3 | Versión 3 6 | V3.4.6.4 | V.4.6.12 | Versión 3 4.6 | Versión 3 6 | |||
En el plano hiperbólico [7,3],



 La familia produce un conjunto paralelo de teselados uniformes y sus teselados duales. Solo hay una alternancia ( snub ) ya que todos los órdenes de ramificación son impares. Se pueden ver muchas otras familias hiperbólicas de teselados uniformes en teselados uniformes en el plano hiperbólico .
La familia produce un conjunto paralelo de teselados uniformes y sus teselados duales. Solo hay una alternancia ( snub ) ya que todos los órdenes de ramificación son impares. Se pueden ver muchas otras familias hiperbólicas de teselados uniformes en teselados uniformes en el plano hiperbólico .
| Teselación heptagonal/triangular uniforme | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetría: [7,3], (*732) | [7,3] + , (732) | ||||||||||
     |      |      |      |      |      |      |      | ||||
 |  |  |  |  |  |  |  | ||||
| {7,3} | t{7,3} | r{7,3} | t{3,7} | {3,7} | rr{7,3} | tr{7,3} | sr{7,3} | ||||
| Duelos uniformes | |||||||||||
     |      |      |      |      |      |      |      | ||||
 |  |  |  |  |  |  |  | ||||
| V7 3 | V3.14.14 | V3.7.3.7 | V6.6.7 | Versión 3 7 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
Diagramas de Coxeter muy extendidos
Un uso incluye una definición muy extendida del uso directo del diagrama de Dynkin que considera a los grupos afines como extendidos , a los grupos hiperbólicos como sobreextendidos y a un tercer nodo como grupos simples muy extendidos . Estas extensiones suelen estar marcadas por un exponente de 1, 2 o 3 + símbolos para el número de nodos extendidos. Esta serie de extensión se puede extender hacia atrás, eliminando secuencialmente los nodos de la misma posición en el gráfico, aunque el proceso se detiene después de eliminar el nodo de ramificación. La familia extendida E 8 es el ejemplo que se muestra con más frecuencia, extendiéndose hacia atrás desde E 3 y hacia adelante hasta E 11 .
El proceso de extensión puede definir una serie limitada de grafos de Coxeter que progresan de finitos a afines a hiperbólicos a lorentzianos. El determinante de las matrices de Cartan determina dónde la serie cambia de finita (positiva) a afín (cero) a hiperbólica (negativa), y termina como un grupo lorentziano, que contiene al menos un subgrupo hiperbólico. [5] Los grupos H n no cristalográficos forman una serie extendida donde H 4 se extiende como un hiperbólico compacto y se sobreextiende en un grupo lorentziano.
Los determinantes de la matriz de Schläfli por rango son: [6]
- det( A 1 n = [2 n −1 ]) = 2 n (Finito para todo n )
- det( A n = [3 n −1 ]) = n + 1 (finito para todo n )
- det( B n = [4,3 n −2 ]) = 2 (finito para todo n )
- det( D n = [3 n −3,1,1 ]) = 4 (finito para todo n )
Los determinantes de la matriz de Schläfli en series excepcionales son:
- det( E n = [3 n −3,2,1 ]) = 9 − n (finito para E 3 (= A 2 A 1 ), E 4 (= A 4 ), E 5 (= D 5 ), E 6 , E 7 y E 8 , afín en E 9 ( ), hiperbólico en E 10 )
- det([3 n −4,3,1 ]) = 2(8 − n ) (finito para n = 4 a 7, afín ( ), e hiperbólico en n = 8.)
- det([3 n −4,2,2 ]) = 3(7 − n ) (finito para n = 4 a 6, afín ( ), e hiperbólico en n = 7.)
- det( F n = [3,4,3 n −3 ]) = 5 − n (finito para F 3 (= B 3 ) a F 4 , afín en F 5 ( ), hiperbólico en F 6 )
- det( G n = [6,3 n −2 ]) = 3 − n (finito para G 2 , afín en G 3 ( ), hiperbólico en G 4 )
| Finito | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rango n | [3 [7] ,3 n −7 ] | [4,3 3 ,3 n −6,1 ] | [3 1,1 ,3,3,3 n −6,1 ] | [3 n −5,2,2 ] | [3 [8] ,3 n −8 ] | [4,3 4 ,3 n −7,1 ] | [3 1,1 ,3,3,3,3 n −7,1 ] | [3 n −5,3,1 ] | En = [3 n −4,2,1 ] |
| 3 | [3 −1,2,1 ] E 3 = A 2 A 1      | ||||||||
| 4 | [3 −1,2,2 ] A 2 2    | [3 −1,3,1 ] Un 3 Un 1        | [3 0,2,1 ] E 4 = A 4      | ||||||
| 5 | [4,3,3,3,3 −1,1 ] segundo 4 un 1          | [3 1,1 ,3,3,3 −1,1 ] re 4 un 1        | [3 0,2,2 ] Un 5      | [3 0,3,1 ] Un 5        | [3 1,2,1 ] E 5 = D 5        | ||||
| 6 | [3 5 ] Un 6      | [ 4,3 4 ] B6          | [3 1,1 ,3,3,3] D 6        | [3 1,2,2 ] E 6        | [4,3,3,3,3,3 −1,1 ] B 5 A 1            | [3 1,1 ,3,3,3,3 −1,1 ] re 5 un 1          | [3 1,3,1 ] D 6          | [3 2,2,1 ] E 6 *          | |
| 7 | [3 [7] ]       | [4,3 3 ,3 1,1 ]           | [3 1,1 ,3,3,3 1,1 ]         | [3 2,2,2 ]         | [3 6 ] Un 7        | [ 4,3 5 ] B7            | [3 1,1 ,3,3,3,3 0,1 ] D 7          | [3 2,3,1 ] E 7 *            | [3 3,2,1 ] E 7 *            |
| 8 | [3 [7] ,3]         | [4,3 3 ,3 2,1 ]             | [3 1,1 ,3,3,3 2,1 ]           | [3 3,2,2 ]           | [3 [8] ] *         | [4,3 4 ,3 1,1 ] *             | [3 1,1 ,3,3,3,3 1,1 ] *           | [3 3,3,1 ] *             | [3 4,2,1 ] E 8 *              |
| 9 | [3 [7] ,3,3] A 6 +++            | [ 4,3 3 ,3 3,1 ] B6 +++                | [3 1,1 ,3,3,3 3,1 ] D 6 +++              | [3 4,2,2 ] E 6 +++              | [3 [8] ,3] *           | [4,3 4 ,3 2,1 ] *               | [3 1,1 ,3,3,3,3 2,1 ] *             | [3 4,3,1 ] *               | [3 5,2,1 ] E 9 = *                |
| 10 | [3 [8] ,3,3] A 7 +++ *              | [4,3 4 , 3 3,1 ] B7 +++ *                  | [3 1,1 ,3,3,3,3 3,1 ] D 7 +++ *                | [3 5,3,1 ] E 7 +++ *                  | [3 6,2,1 ] E 10 = *                  | ||||
| 11 | [3 7,2,1 ] E 11 = E 8 +++ *                    | ||||||||
| Det ( Mn ) | 7(7− n ) | 2(7− n ) | 4(7− n ) | 3(7− n ) | 8(8− n ) | 2(8− n ) | 4(8− n ) | 2(8− n ) | 9− n |
Plegado geométrico
| φ A : A Γ → A Γ' para tipos finitos | |||
|---|---|---|---|
| Γ | Γ' | Descripción plegable | Diagramas de Coxeter-Dynkin |
| Yo 2 ( h ) | Γ(h) | Plegado diedro |  |
| Bn | Un 2n | (yo,s n ) | |
| D n+1 , A 2n-1 | (A 3 ,±ε) | ||
| F4 | E6 | (A 3 ,±ε) | |
| H4 | E8 | (A 4 ,±ε) | |
| H3 | D6 | ||
| H2 | Un 4 | ||
| G2 | Un 5 | (A 5 ,±ε) | |
| D4 | (D 4 ,±ε) | ||
| φ: A Γ + → A Γ' + para tipos afines | |||
| Localmente trivial |  | ||
| (yo,s n ) | |||
| , | (A 3 ,±ε) | ||
| , | (A 3 ,±ε) | ||
| (yo,s n ) | |||
| (I,s n ) y (I,s 0 ) | |||
| (A 3 ,ε) y (I,s 0 ) | |||
| (A3 , ε) y (A3 , ε') | |||
| (A3 , −ε) y (A3 , −ε') | |||
| (yo 1 ) | |||
| , | (A 3 ,±ε) | ||
| , | (A 5 ,±ε) | ||
| , | (B3 , ±ε) | ||
| , | (D 4 ,±ε) | ||
Un diagrama de Coxeter-Dynkin (finito, afín o hiperbólico) (simplemente enlazado) que tiene una simetría (que satisface una condición, a continuación) puede ser cocienteado por la simetría, produciendo un nuevo diagrama, generalmente enlazado de forma múltiple, con el proceso llamado "plegado". [8] [9]
Por ejemplo, en el plegado de D 4 a G 2 , la arista en G 2 apunta desde la clase de los 3 nodos externos (valencia 1), a la clase del nodo central (valencia 3). Y E 8 se pliega en 2 copias de H 4 , la segunda copia escalada por τ . [10]
Geométricamente, esto corresponde a proyecciones ortogonales de politopos y teselaciones uniformes. En particular, cualquier diagrama de Coxeter-Dynkin finito y simplemente enlazado se puede plegar a I 2 ( h ), donde h es el número de Coxeter , que corresponde geométricamente a una proyección al plano de Coxeter .
 Algunos plegamientos hiperbólicos |
Reflexiones complejas
Los diagramas de Coxeter-Dynkin se han extendido al espacio complejo , C n donde los nodos son reflexiones unitarias de período mayor que 2. Los nodos están etiquetados por un índice, que se supone que es 2 para la reflexión real ordinaria si se suprime. Coxeter escribe el grupo complejo, p[q]r, como diagrama



 . [11]
. [11]
Un politopo complejo regular unidimensional se representa como , que tiene p vértices. Su representación real es un polígono regular , { p }. Su simetría es p [] o
, que tiene p vértices. Su representación real es un polígono regular , { p }. Su simetría es p [] o , orden p . Un generador de operadores unitarios para
, orden p . Un generador de operadores unitarios para se ve como una rotación de 2 π / p radianes en sentido antihorario y una
se ve como una rotación de 2 π / p radianes en sentido antihorario y una El borde se crea mediante aplicaciones secuenciales de una única reflexión unitaria. Un generador de reflexión unitaria para un 1-politopo con p vértices es e 2 π i / p = cos(2 π / p ) + i sin(2 π / p ) . Cuando p = 2, el generador es e π i = –1, lo mismo que una reflexión puntual en el plano real.
El borde se crea mediante aplicaciones secuenciales de una única reflexión unitaria. Un generador de reflexión unitaria para un 1-politopo con p vértices es e 2 π i / p = cos(2 π / p ) + i sin(2 π / p ) . Cuando p = 2, el generador es e π i = –1, lo mismo que una reflexión puntual en el plano real.
En un politopo superior, p {} o representa un elemento de borde p , con un borde 2, {} o
representa un elemento de borde p , con un borde 2, {} o , que representa un borde real ordinario entre dos vértices.
, que representa un borde real ordinario entre dos vértices.
 1-politopos complejos,  , representados en el plano de Argand como polígonos regulares para p = 2, 3, 4, 5 y 6, con vértices negros. El centroide de los p vértices se muestra en rojo. Los lados de los polígonos representan una aplicación del generador de simetría, que asigna cada vértice a la siguiente copia en sentido antihorario. Estos lados poligonales no son elementos de borde del politopo, ya que un 1-politopo complejo no puede tener bordes (a menudo es un borde complejo) y solo contiene elementos de vértice. , representados en el plano de Argand como polígonos regulares para p = 2, 3, 4, 5 y 6, con vértices negros. El centroide de los p vértices se muestra en rojo. Los lados de los polígonos representan una aplicación del generador de simetría, que asigna cada vértice a la siguiente copia en sentido antihorario. Estos lados poligonales no son elementos de borde del politopo, ya que un 1-politopo complejo no puede tener bordes (a menudo es un borde complejo) y solo contiene elementos de vértice. |
Un polígono complejo regular en , tiene la forma p { q } r o diagrama de Coxeter



 . El grupo de simetría de un polígono regular complejo
. El grupo de simetría de un polígono regular complejo



 no se llama grupo de Coxeter , sino grupo de Shephard , un tipo de grupo de reflexión complejo . El orden de p [ q ] r es . [13]
no se llama grupo de Coxeter , sino grupo de Shephard , un tipo de grupo de reflexión complejo . El orden de p [ q ] r es . [13]
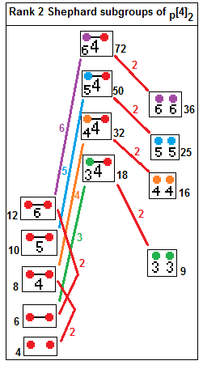
Los grupos de Shephard de rango 2 son: 2 [ q ] 2 , p [4] 2 , 3 [3 ] 3 , 3 [6] 2 , 3 [4] 3 , 4 [3] 4 , 3 [8] 2 , 4 [6] 2 , 4 [4] 3 , 3 [ 5 ] 3 , 5 [3] 5 , 3 [10] 2 , 5 [6] 2 y 5 [4] 3 o

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 de orden 2 q , 2 p 2 , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 y 1800 respectivamente.
de orden 2 q , 2 p 2 , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 y 1800 respectivamente.
El grupo de simetría p 1 [ q ] p 2 está representado por 2 generadores R 1 , R 2 , donde:
- R1p1 = R2p2 = yo .
Si q es par, (R 2 R 1 ) q /2 = (R 1 R 2 ) q /2 . Si q es impar, (R 2 R 1 ) (q-1)/2 R 2 = (R 1 R 2 ) ( q -1)/2 R 1 . Cuando q es impar, p 1 = p 2 .
El grupo
 o [1 1 1] p se define por 3 reflexiones unitarias de período 2 {R 1 , R 2 , R 3 }:
o [1 1 1] p se define por 3 reflexiones unitarias de período 2 {R 1 , R 2 , R 3 }:
- R12 = R12 = R32 = ( R1R2 ) 3 = ( R2R3 ) 3 = ( R3R1 ) 3 = ( R1R2R3R1 ) p = 1 .
El periodo p puede verse como una doble rotación en términos reales .
Un grupo similar

 o [1 1 1] (p) se define por 3 reflexiones unitarias de período 2 {R 1 , R 2 , R 3 }:
o [1 1 1] (p) se define por 3 reflexiones unitarias de período 2 {R 1 , R 2 , R 3 }:
- R12 = R12 = R32 = ( R1R2 ) 3 = ( R2R3 ) 3 = ( R3R1 ) 3 = ( R1R2R3R2 ) p = 1 .
Véase también
- Grupo Coxeter
- Triángulo de Schwarz
- Tetraedro de Goursat
- Diagrama de Dynkin
- Politopo uniforme
- Construcción de Wythoff y símbolo de Wythoff
Referencias
- ^ Hall, Brian C. (2003), Grupos de Lie, álgebras de Lie y representaciones: una introducción elemental , Springer, ISBN 978-0-387-40122-5
- ^ Borovik, Alexandre; Borovik, Anna (2010). Espejos y reflejos . Springer. págs. 118–119.
- ^ Coxeter, Regular Polytopes , (3.ª edición, 1973), edición de Dover, ISBN 0-486-61480-8 , sec. 7.7, pág. 133, Criterio de Schläfli
- ^ Lannér F., Sobre complejos con grupos transitivos de automorfismos , Medd. Universidad de Lund. Estera. Sem. [Com. Sem. Matemáticas. Univ. Lund], 11 (1950), 1–71
- ^ De Buyl, Sophie (2006). "Álgebras de Kac-Moody en teoría M". arXiv : hep-th/0608161 .
- ^ Determinantes de Cartan-Gram para los grupos de Lie simples, Wu, Alfred C. T, The American Institute of Physics, noviembre de 1982
- ^ John Crisp , ' Mapas inyectivos entre grupos de Artin ', en Teoría de grupos en Australia, Actas del Año Especial sobre Teoría de Grupos Geométricos, (Universidad Nacional Australiana, Canberra, Australia, 1996), Postscript Archivado el 16 de octubre de 2005 en Wayback Machine , págs. 13-14, y googlebook, Teoría de grupos geométricos en Australia, pág. 131
- ^ Zuber, Jean-Bernard (1998). "Diagramas de Dynkin generalizados y sistemas de raíces y su plegamiento". Teoría de campos topológicos : 28–30. arXiv : hep-th/9707046 . Código Bibliográfico :1998tftp.conf..453Z. CiteSeerX 10.1.1.54.3122 .
- ^ Dechant, Pierre-Philippe; Boehm, Celine; Twarock, Reidun (2013). "Extensiones afines de grupos de Coxeter no cristalográficos inducidas por proyección". Journal of Mathematical Physics . 54 (9): 093508. arXiv : 1110.5228 . Bibcode :2013JMP....54i3508D. doi :10.1063/1.4820441. S2CID 59469917.
- ^ Dechant, Pierre-Philippe (2017). "La geometría E 8 desde una perspectiva de Clifford". Avances en álgebras de Clifford aplicadas . 27 : 397–421. doi : 10.1007/s00006-016-0675-9 .
- ^ Coxeter, Politopos regulares complejos , segunda edición, (1991)
- ^ Coxeter, Politopos regulares complejos, pág. 177, Tabla III
- ^ Grupos Unitarios de Reflexión , p.87
- ^
- ^ Si entonces así y
Lectura adicional
- James E. Humphreys , Grupos de reflexión y grupos de Coxeter , Cambridge studies in advanced mathematics, 29 (1990)
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1], Googlebooks [2]
- (Documento 17) Coxeter , La evolución de los diagramas de Coxeter-Dynkin , [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
- Coxeter , La belleza de la geometría: doce ensayos , Dover Publications, 1999, ISBN 978-0-486-40919-1 (Capítulo 3: Construcción de Wythoff para politopos uniformes)
- Coxeter , Politopos regulares (1963), Macmillan Company
- Politopos regulares , tercera edición (1973), edición Dover, ISBN 0-486-61480-8 (Capítulo 5: El caleidoscopio y Sección 11.3 Representación mediante gráficos)
- HSM Coxeter y WOJ Moser, Generadores y relaciones para grupos discretos, 4.ª edición, Springer-Verlag, Nueva York, 1980
- Norman Johnson , Geometrías y transformaciones , capítulos 11, 12 y 13, preimpresión 2011
- NW Johnson , R. Kellerhals , JG Ratcliffe, ST Tschantz, El tamaño de un símplex hiperbólico de Coxeter , Transformation Groups, 1999, Volumen 4, Número 4, págs. 329–353 [3] [4]
- Norman W. Johnson y Asia Ivic Weiss Enteros cuadráticos y grupos de Coxeter Archivado el 26 de marzo de 2023 en Wayback Machine PDF Can. J. Math. Vol. 51 (6), 1999, págs. 1307–1336
Enlaces externos
- Weisstein, Eric W. "Diagrama de Coxeter-Dynkin". MathWorld .
- Discusión de octubre de 1978 sobre la historia de los diagramas de Coxeter por Coxeter y Dynkin en Toronto , Canadá ; Colección Eugene Dynkin de entrevistas matemáticas, Biblioteca de la Universidad de Cornell .




![{\displaystyle \left[{\begin{matriz}2&a_{12}\\a_{21}&2\end{matriz}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609b9b4324da49c4903330c430b14203d6f971cb)

![{\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![{\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/934421fb85592c1788a92b7d350953dd2ca94b5e)
![{\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f92222bfe2eeefe46dddcc56620241d8efd5ef1)
![{\displaystyle \left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db286eb5ca733d2b6ab1c5f194f03593440b5b3a)

![{\displaystyle \left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dcf61f3b1fac33acafec6ac2d577c66f9f69306)
![{\displaystyle \left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a16582176db9cb488aa850d0b0a970ff0a62cd6)

![{\displaystyle \left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8548776ee20b1e4a17df57227d372025e5bcbd65)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b77e92921199a57f051014d4938de1a0d22ef38)
![{\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51483cac6134b485a8a8ea0d9e2fee62fda6d13a)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {2}}}}\\-{\sqrt {2+{\sqrt {2}}}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76feec8c86bbfeb5ce6439e1293efa582074902f)

![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {(5+{\sqrt {5}})/2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cae955a07738bbf5a75ab02e8a5f2597346acaa)

![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {3}}}}\\-{\sqrt {2+{\sqrt {3}}}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f97b80af547d6ad0bcd4cc495671b2f7535d98)

![{\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71dd5a3c2a3aa08ab89d00e05a0afe4db4876ff8)



![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd86323eaf497d2bb96f757556dd458abd5863cf)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\cosh(2\lambda )\\-2\cosh(2\lambda )&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7051e92a35badbc10b3096bd2e43a4e328f19674)