Entalpía

Termodinámica
La clásica máquina térmica de Carnot
Sucursales Clásico Estadístico Químico Termodinámica cuántica Equilibrio  / No equilibrio
Leyes Cero Primero Segundo Tercero
Sistemas Sistema cerrado Sistema abierto Sistema aislado Estado Ecuación de estado Gas ideal Gas real Estado de la materia Fase (materia) Equilibrio Controlar el volumen Instrumentos Procesos Isobárico Isocórico Isotermal Adiabático Isentrópico Isentálpico Cuasistático Politrópico Expansión libre Reversibilidad Irreversibilidad Endorreversibilidad Ciclos Motores térmicos Bombas de calor Eficiencia térmica
Propiedades del sistema Nota: Variables conjugadas en cursiva Diagramas de propiedades Propiedades intensivas y extensivas Funciones del proceso Trabajar Calor Funciones del estado Temperatura  / Entropía  ( introducción ) Presión  / Volumen Potencial químico  / Número de partículas Calidad del vapor Propiedades reducidas
Propiedades del material Bases de datos de propiedades Capacidad calorífica específica  ${\estilo de visualización c=}$ ${\estilo de visualización T}$ ${\displaystyle \s parcial}$ ${\estilo de visualización N}$ ${\displaystyle \parcial T}$ Compresibilidad  ${\displaystyle \beta =-}$ ${\estilo de visualización 1}$ ${\displaystyle \V parcial}$ ${\estilo de visualización V}$ ${\displaystyle \p parcial}$ Expansión térmica  ${\displaystyle \alpha =}$ ${\estilo de visualización 1}$ ${\displaystyle \V parcial}$ ${\estilo de visualización V}$ ${\displaystyle \parcial T}$
Ecuaciones Teorema de Carnot Teorema de Clausius Relación fundamental Ley de los gases ideales Relaciones de Maxwell Relaciones recíprocas de Onsager Ecuaciones de Bridgman Tabla de ecuaciones termodinámicas
Potenciales Energía libre Entropía libre Energía interna ${\displaystyle U(S,V)}$ Entalpía ${\displaystyle H(S,p)=U+pV}$ Energía libre de Helmholtz ${\displaystyle A(T,V)=U-TS}$ Energía libre de Gibbs ${\displaystyle G(T,p)=H-TS}$
Historia Cultura Historia General Entropía Leyes de los gases Máquinas de "movimiento perpetuo" Filosofía Entropía y tiempo Entropía y vida Trinquete browniano El demonio de Maxwell Paradoja de la muerte por calor La paradoja de Loschmidt Sinergética Teorías Teoría calórica Vis viva ("fuerza viva") Equivalente mecánico del calor Fuerza motriz Publicaciones clave Una investigación sobre la fuente... la fricción Sobre el equilibrio de sustancias heterogéneas Reflexiones sobre la fuerza motriz del fuego Líneas de tiempo Termodinámica Motores térmicos Arte Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Boltzmann Bridgman Carathéodory Carnot Clapeyron Clausius de Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

Entalpía ( / ˈ ɛ n θ əl p i / ^ⓘ ) es la suma de la energía internadeunsistema termodinámicoy el producto de supresiónyvolumen.^[1]Es unafunción de estadoentermodinámicautilizada en muchas mediciones en sistemas químicos, biológicos y físicos a una presión externa constante, que es proporcionada convenientemente por la gran atmósfera ambiental. El término presión-volumen expresa eltrabajoque se realizó contra la presión externa constantepara establecer las dimensiones físicas del sistema desdehasta un volumen final(como), es decir, para hacerle espacio desplazando sus alrededores.^[2][3]El término presión-volumen es muy pequeño para sólidos y líquidos en condiciones comunes, y bastante pequeño para gases. Por lo tanto, la entalpía es un sustituto dela energíaen los sistemas químicos;enlace,red,solvatacióny otras "energías" químicas son en realidad diferencias de entalpía. Como función de estado, la entalpía depende solo de la configuración final de la energía interna, la presión y el volumen, no del camino tomado para lograrlo. ${\displaystyle W}$${\displaystyle P_{ext}}$${\displaystyle V_{system,initial}=0}$${\displaystyle V_{system,final}}$${\displaystyle W=P_{ext}\Delta V}$

En el Sistema Internacional de Unidades (SI), la unidad de medida de la entalpía es el julio . Otras unidades convencionales históricas que todavía se utilizan son la caloría y la unidad térmica británica (BTU).

La entalpía total de un sistema no se puede medir directamente porque la energía interna contiene componentes que son desconocidos, no son fácilmente accesibles o no son de interés para el problema termodinámico en cuestión. En la práctica, un cambio en la entalpía es la expresión preferida para mediciones a presión constante, porque simplifica la descripción de la transferencia de energía . Cuando también se evita la transferencia de materia dentro o fuera del sistema y no se realiza ningún trabajo eléctrico o mecánico (eje de agitación o bombeo de elevación), a presión constante el cambio de entalpía es igual a la energía intercambiada con el medio ambiente por calor .

En química, la entalpía estándar de reacción es el cambio de entalpía cuando los reactivos en sus estados estándar ( p = 1 bar  ; usualmente T = 298 K ) cambian a productos en sus estados estándar. ^[4] Esta cantidad es el calor estándar de reacción a presión y temperatura constantes, pero se puede medir por métodos calorimétricos incluso si la temperatura varía durante la medición, siempre que la presión y temperatura inicial y final correspondan al estado estándar. El valor no depende del camino desde el estado inicial al final porque la entalpía es una función del estado .

Las entalpías de las sustancias químicas se indican generalmente para una presión de 1 bar (100 kPa) como estado estándar. Las entalpías y los cambios de entalpía de las reacciones varían en función de la temperatura, ^[5] pero las tablas generalmente indican los calores estándar de formación de sustancias a 25 °C (298 K). Para los procesos endotérmicos (que absorben calor), el cambio Δ H es un valor positivo; para los procesos exotérmicos (que liberan calor), es negativo.

La entalpía de un gas ideal es independiente de su presión o volumen y depende únicamente de su temperatura, que se correlaciona con su energía térmica. Los gases reales a temperaturas y presiones comunes suelen aproximarse mucho a este comportamiento, lo que simplifica el diseño y el análisis termodinámicos prácticos.

La palabra "entalpía" se deriva de la palabra griega enthalpein , que significa calentar. ^{[6] [7]}

La entalpía H de un sistema termodinámico se define como la suma de su energía interna y el producto de su presión y volumen: ^[1]

$${\displaystyle H=U+pV,}$$donde U es la energía interna , p es la presión y V es el volumen del sistema; p V a veces se denomina energía de presión Ɛ _p  . ^[8]

La entalpía es una propiedad extensiva ; es proporcional al tamaño del sistema (para sistemas homogéneos). Como propiedades intensivas , la entalpía específica , h = ⁠  yo /metro⁠ ,se refiere a una unidad demasa mdel sistema, y ​​laentalpía molar, H _m = ⁠  yo /norte⁠ ,dondenes el número demoles. Para sistemas no homogéneos, la entalpía es la suma de las entalpías de los subsistemas componentes: donde$${\displaystyle H=\sum _{k}H_{k}\;,}$$

H es la entalpía total de todos los subsistemas,

k se refiere a los diversos subsistemas,

H _k se refiere a la entalpía de cada subsistema.

Un sistema cerrado puede estar en equilibrio termodinámico en un campo gravitacional estático , de modo que su presión p varía continuamente con la altitud , mientras que, debido al requisito de equilibrio, su temperatura T es invariante con la altitud. (Correspondientemente, la densidad de energía potencial gravitatoria del sistema también varía con la altitud). Entonces la suma de entalpías se convierte en una integral : donde$${\displaystyle H=\int \left(\rho \,h\right)\,\mathrm {d} V\;,}$$

ρ (" rho ") es la densidad (masa por unidad de volumen),

h es la entalpía específica (entalpía por unidad de masa),

( ρh ) representa la densidad de entalpía (entalpía por unidad de volumen),

d V denota un elemento infinitesimalmente pequeño de volumen dentro del sistema, por ejemplo, el volumen de una capa horizontal infinitesimalmente delgada.

La integral representa por tanto la suma de las entalpías de todos los elementos del volumen.

La entalpía de un sistema homogéneo cerrado es su función energética H ( S , p ) , con su entropía S [ p ] y su presión p como variables de estado naturales que proporcionan una relación diferencial para d H de la forma más simple, derivada de la siguiente manera. Partimos de la primera ley de la termodinámica para sistemas cerrados para un proceso infinitesimal:

$${\displaystyle \mathrm {d} U=\mathrm {\delta } \,Q-\mathrm {\delta } \,W\;,}$$

dónde

δ Q es una pequeña cantidad de calor agregada al sistema,

δ W es una pequeña cantidad de trabajo realizado por el sistema.

En un sistema homogéneo en el que sólo se consideran procesos reversibles o transferencia de calor pura, la segunda ley de la termodinámica da δ Q = T d S , donde T es la temperatura absoluta y d S el cambio infinitesimal en la entropía S del sistema. Además, si sólo se realiza p V trabajo, δ W = p  d V . Como resultado,

$${\displaystyle \mathrm {d} U=T\,\mathrm {d} S-p\,\mathrm {d} V~.}$$

Sumando d( p V ) a ambos lados de esta expresión se obtiene

$${\displaystyle \mathrm {d} U+\mathrm {d} (p\,V)=T\,\mathrm {d} S-p\,\mathrm {d} V+\mathrm {d} (p\,V)\;,}$$

o

$${\displaystyle \mathrm {d} (U+p\,V)=T\,\mathrm {d} S+V\,\mathrm {d} p~.}$$

Entonces

$${\displaystyle \mathrm {d} H(S,\,p)=T\,\mathrm {d} S+V\,\mathrm {d} p~}$$

y los coeficientes de las variables naturales diferenciales d S y d p son sólo las variables individuales T y V .

La expresión anterior de d H en términos de entropía y presión puede resultar desconocida para algunos lectores. También existen expresiones en términos de variables más directamente mensurables, como la temperatura y la presión: ^{[9] (pág. 88) [10]}

$${\displaystyle \mathrm {d} H=C_{\mathsf {p}}\,\mathrm {d} T+V\,(1-\alpha T)\,\mathrm {d} p~.}$$

Aquí C _p es la capacidad calorífica a presión constante y α es el coeficiente de expansión térmica (cúbica) :

$${\displaystyle \alpha ={\frac {\,1\,}{V}}\left({\frac {\partial V}{\,\partial T\,}}\right)_{\mathsf {p}}~.}$$

Con esta expresión se puede, en principio, determinar la entalpía si C _p y V se conocen como funciones de p y T  . Sin embargo la expresión es más complicada porque T no es una variable natural para la entalpía H .${\displaystyle \;\mathrm {d} H=T\,\mathrm {d} S+V\,\mathrm {d} p\;}$

A presión constante, de modo que Para un gas ideal , se reduce a esta forma incluso si el proceso implica un cambio de presión, porque α T = 1 . ^{[nota 1]}${\displaystyle \;\mathrm {d} P=0\;}$${\displaystyle \;\mathrm {d} H=C_{\mathsf {p}}\,\mathrm {d} T~.}$${\displaystyle \;\mathrm {d} H\;}$

En una forma más general, la primera ley describe la energía interna con términos adicionales que involucran el potencial químico y el número de partículas de varios tipos. El enunciado diferencial para d H se convierte entonces en

$${\displaystyle \mathrm {d} H=T\,\mathrm {d} S+V\,\mathrm {d} p+\sum _{i}\mu _{i}\,\mathrm {d} N_{i}\;,}$$

donde μ _i es el potencial químico por partícula para una  partícula de tipo i , y N _i es el número de dichas partículas. El último término también puede escribirse como μ _i  d n _i (siendo d n _{i  0} el número de moles del componente i añadido al sistema y, en este caso, μ _i el potencial químico molar) o como μ _i d m _i (siendo d m _i la masa del componente i añadido al sistema y, en este caso, μ _i el potencial químico específico).

La entalpía, H ( S [ p ], p , { N _i } ) , expresa la termodinámica de un sistema en la representación de energía . Como función del estado , sus argumentos incluyen tanto una variable de estado intensiva como varias variables de estado extensivas . Se dice que las variables de estado S [ p ] , p y { N _i } son las variables de estado naturales en esta representación. Son adecuadas para describir procesos en los que están determinadas por factores del entorno. Por ejemplo, cuando una parcela virtual de aire atmosférico se mueve a una altitud diferente, la presión que la rodea cambia y el proceso suele ser tan rápido que hay muy poco tiempo para la transferencia de calor. Esta es la base de la llamada aproximación adiabática que se utiliza en meteorología . ^[11]

Conjugada con la entalpía, con estos argumentos, la otra función característica de estado de un sistema termodinámico es su entropía, como función, S [ p ]( H , p , {N _i }) , de la misma lista de variables de estado, excepto que la entropía, S [ p ] , se reemplaza en la lista por la entalpía, H. Expresa la representación de la entropía . Se dice que las variables de estado H , p y { N _i } son las variables de estado naturales en esta representación. Son adecuadas para describir procesos en los que se controlan experimentalmente. Por ejemplo, H y p se pueden controlar permitiendo la transferencia de calor y variando solo la presión externa sobre el pistón que fija el volumen del sistema. ^{[12] [13] [14]}

El término U es la energía del sistema, y ​​el término p V puede interpretarse como el trabajo que se requeriría para "hacer espacio" para el sistema si la presión del entorno permaneciera constante. Cuando un sistema, por ejemplo, n moles de un gas de volumen V a presión p y temperatura T , se crea o se lleva a su estado actual desde el cero absoluto , se debe suministrar energía igual a su energía interna U más p V , donde p V es el trabajo realizado para empujar contra la presión ambiental (atmosférica).

En física y mecánica estadística puede ser más interesante estudiar las propiedades internas de un sistema de volumen constante y por lo tanto se utiliza la energía interna. ^{[15] [16]} En química , los experimentos a menudo se realizan a presión atmosférica constante , y el trabajo presión-volumen representa un intercambio de energía pequeño y bien definido con la atmósfera, de modo que Δ H es la expresión apropiada para el calor de reacción . Para un motor térmico , el cambio en su entalpía después de un ciclo completo es igual a cero, ya que el estado final e inicial son iguales.

Para discutir la relación entre el aumento de entalpía y el suministro de calor, volvemos a la primera ley para sistemas cerrados, con la convención de signos de la física: d U = δ Q − δ W , donde el calor δ Q es suministrado por conducción, radiación, calentamiento Joule . Lo aplicamos al caso especial con una presión constante en la superficie. En este caso el trabajo está dado por p d V (donde p es la presión en la superficie, d V es el aumento del volumen del sistema). Los casos de interacción electromagnética de largo alcance requieren más variables de estado en su formulación, y no se consideran aquí. En este caso la primera ley dice: $${\displaystyle \mathrm {d} U=\mathrm {\delta } \,Q-p\,\mathrm {d} V~.}$$

Ahora,$${\displaystyle \mathrm {d} H=\mathrm {d} U+\mathrm {d} (p\,V)~.}$$

Entonces$${\displaystyle {\begin{aligned}\mathrm {d} H&=\mathrm {\delta } Q+V\,\mathrm {d} p+p\,\mathrm {d} V-p\,\mathrm {d} V\\&=\mathrm {\delta } Q+V\,\mathrm {d} p~.\end{aligned}}}$$

Si el sistema está bajo presión constante , d p = 0 y en consecuencia, el aumento de entalpía del sistema es igual al calor añadido:

$${\displaystyle \mathrm {d} H=\mathrm {\delta } \,Q}$$Por esta razón , en el siglo XIX se utilizó el término hoy obsoleto de contenido calorífico para referirse a la entalpía.

En termodinámica, se puede calcular la entalpía determinando los requisitos para crear un sistema a partir de la "nada"; el trabajo mecánico requerido, p V , difiere según las condiciones que se dan durante la creación del sistema termodinámico .

Se debe suministrar energía para eliminar partículas de los alrededores y hacer espacio para la creación del sistema, suponiendo que la presión p permanece constante; este es el término p V . La energía suministrada también debe proporcionar el cambio en la energía interna, U , que incluye energías de activación , energías de ionización, energías de mezcla, energías de vaporización, energías de enlace químico, etc. En conjunto, estos constituyen el cambio en la entalpía U + p V . Para sistemas a presión constante, sin trabajo externo realizado aparte del trabajo p V , el cambio en la entalpía es el calor recibido por el sistema.

Para un sistema simple con un número constante de partículas a presión constante, la diferencia de entalpía es la cantidad máxima de energía térmica derivable de un proceso termodinámico isobárico. ^[17]

La entalpía total de un sistema no se puede medir directamente; en su lugar, se mide el cambio de entalpía de un sistema . El cambio de entalpía se define mediante la siguiente ecuación: donde$${\displaystyle \Delta H=H_{\mathsf {f}}-H_{\mathsf {i}}\,,}$$

Δ H es el "cambio de entalpía",

H _f es la entalpía final del sistema (en una reacción química, la entalpía de los productos o del sistema en equilibrio),

H _i es la entalpía inicial del sistema (en una reacción química, la entalpía de los reactivos).

Para una reacción exotérmica a presión constante , el cambio de entalpía del sistema, Δ H , es negativo debido a que los productos de la reacción tienen una entalpía menor que los reactivos, y es igual al calor liberado en la reacción si no se realiza trabajo eléctrico o de eje. En otras palabras, la disminución general de la entalpía se logra mediante la generación de calor. ^[18] Por el contrario, para una reacción endotérmica a presión constante , Δ H es positivo e igual al calor absorbido en la reacción.

De la definición de entalpía como H = U + p V , el cambio de entalpía a presión constante es Δ H = Δ U + p Δ V . Sin embargo, para la mayoría de las reacciones químicas, el término de trabajo p Δ V es mucho menor que el cambio de energía interna Δ U , que es aproximadamente igual a Δ H . ​​Como ejemplo, para la combustión de monóxido de carbono 2 CO(g) + O ₂ (g) → 2 CO ₂ (g) , Δ H = −566,0 kJ y Δ U = −563,5 kJ. ^[19] Dado que las diferencias son tan pequeñas, las entalpías de reacción a menudo se describen como energías de reacción y se analizan en términos de energías de enlace .

La entalpía específica de un sistema uniforme se define como h = ⁠ yo/ metro ⁠ dondemes la masa del sistema. Launidad SIpara la entalpía específica es el julio por kilogramo. Puede expresarse en otras cantidades específicas mediante h = u + pv ,dondeues laenergía interna,pes la presión yvesel volumen específico, que es igual a ⁠  1 /ρ⁠ , donde ρ es la densidad .

Un cambio de entalpía describe el cambio de entalpía observado en los componentes de un sistema termodinámico cuando experimenta una transformación o reacción química. Es la diferencia entre la entalpía después de que el proceso se ha completado, es decir, la entalpía de los productos suponiendo que la reacción se completa, y la entalpía inicial del sistema, es decir, los reactivos. Estos procesos se especifican únicamente por sus estados inicial y final, de modo que el cambio de entalpía para el proceso inverso es el negativo del del proceso directo.

Un cambio de entalpía estándar común es la entalpía de formación , que se ha determinado para una gran cantidad de sustancias. Los cambios de entalpía se miden y recopilan de manera rutinaria en obras de referencia químicas y físicas, como el CRC Handbook of Chemistry and Physics . A continuación, se presenta una selección de cambios de entalpía comúnmente reconocidos en termodinámica.

Cuando se utiliza en estos términos reconocidos, el cambio de calificador suele omitirse y la propiedad se denomina simplemente entalpía de "proceso" . Dado que estas propiedades se utilizan a menudo como valores de referencia, es muy común citarlas para un conjunto estandarizado de parámetros ambientales o condiciones estándar , que incluyen:

• Una presión de una atmósfera (1 atm o 1013,25 hPa) o 1 bar
• Una temperatura de 25 °C o 298,15 K
• Una concentración de 1,0 M cuando el elemento o compuesto está presente en solución.
• Elementos o compuestos en sus estados físicos normales, es decir, estado estándar.

Para tales valores estandarizados, el nombre de la entalpía suele ir precedido del término estándar , por ejemplo, entalpía estándar de formación .

Entalpía de reacción : se define como el cambio de entalpía observado en un componente de un sistema termodinámico cuando un mol de sustancia reacciona completamente.

Entalpía de formación : se define como el cambio de entalpía observado en un componente de un sistema termodinámico cuando se forma un mol de un compuesto a partir de sus antecedentes elementales.

Entalpía de combustión : se define como el cambio de entalpía observado en un componente de un sistema termodinámico cuando un mol de una sustancia se quema completamente con oxígeno.

Entalpía de hidrogenación : se define como el cambio de entalpía observado en un componente de un sistema termodinámico cuando un mol de un compuesto insaturado reacciona completamente con un exceso de hidrógeno para formar un compuesto saturado .

Entalpía de atomización : se define como el cambio de entalpía necesario para separar completamente un mol de una sustancia en sus átomos constituyentes .

Entalpía de neutralización : se define como el cambio de entalpía observado en un componente de un sistema termodinámico cuando se forma un mol de agua cuando reaccionan un ácido y una base.

Entalpía estándar de solución : se define como el cambio de entalpía observado en un componente de un sistema termodinámico cuando un mol de soluto se disuelve completamente en un exceso de solvente, de modo que la solución está en dilución infinita.

Entalpía estándar de desnaturalización (bioquímica) : se define como el cambio de entalpía necesario para desnaturalizar un mol de compuesto.

Entalpía de hidratación : se define como el cambio de entalpía observado cuando un mol de iones gaseosos se disuelve completamente en agua formando un mol de iones acuosos.

Entalpía de fusión : se define como el cambio de entalpía necesario para cambiar completamente el estado de un mol de sustancia de sólido a líquido.

Entalpía de vaporización : se define como el cambio de entalpía necesario para cambiar completamente el estado de un mol de sustancia de líquido a gas.

Entalpía de sublimación : se define como el cambio de entalpía necesario para cambiar completamente el estado de un mol de sustancia de sólido a gas.

Entalpía reticular : se define como la energía necesaria para separar un mol de un compuesto iónico en iones gaseosos separados a una distancia infinita (es decir, sin fuerza de atracción).

Entalpía de mezcla : se define como el cambio de entalpía al mezclar dos sustancias químicas (que no reaccionan).

En los sistemas termodinámicos abiertos , la masa (de sustancias) puede fluir hacia dentro y hacia fuera de los límites del sistema. La primera ley de la termodinámica para sistemas abiertos establece: El aumento de la energía interna de un sistema es igual a la cantidad de energía añadida al sistema por la masa que fluye hacia dentro y por el calor, menos la cantidad perdida por la masa que fluye hacia fuera y en forma de trabajo realizado por el sistema:

$${\displaystyle \mathrm {d} U=\mathrm {\delta } \,Q+\mathrm {d} U_{\mathsf {in}}-\mathrm {d} U_{\mathsf {out}}-\mathrm {\delta } \,W\,,}$$

donde U _in es la energía interna promedio que entra al sistema y U _out es la energía interna promedio que sale del sistema.

La región del espacio encerrada por los límites del sistema abierto se suele llamar volumen de control y puede corresponder o no a paredes físicas. Si elegimos la forma del volumen de control de modo que todo el flujo de entrada o salida se produzca perpendicular a su superficie, entonces el flujo de masa hacia el sistema realiza un trabajo como si fuera un pistón de fluido que empuja la masa hacia el sistema, y ​​el sistema realiza un trabajo sobre el flujo de masa hacia fuera como si estuviera impulsando un pistón de fluido. Entonces, hay dos tipos de trabajo realizado: el trabajo de flujo descrito anteriormente, que se realiza sobre el fluido (a esto también se le suele llamar trabajo p V ), y el trabajo mecánico ( trabajo de eje ), que puede realizarse sobre algún dispositivo mecánico como una turbina o una bomba.

Estos dos tipos de trabajo se expresan en la ecuación$${\displaystyle \mathrm {\delta } \,W=\mathrm {d} (p_{\mathsf {out}}V_{\mathsf {out}})-\mathrm {d} (p_{\mathsf {in}}V_{\mathsf {in}})+\mathrm {\delta } \,W_{\mathsf {shaft}}~.}$$

Sustituyendo en la ecuación anterior el volumen de control (cv) obtenemos:

$${\displaystyle \mathrm {d} U_{\mathsf {cv}}=\mathrm {\delta } \,Q+\mathrm {d} U_{\mathsf {in}}+\mathrm {d} \left(p_{\mathsf {in}}V_{\mathsf {in}}\right)-\mathrm {d} U_{\mathsf {out}}-\mathrm {d} \left(p_{\mathsf {out}}V_{\mathsf {out}}\right)-\mathrm {\delta } W_{\mathsf {shaft}}~.}$$

La definición de entalpía, H , nos permite utilizar este potencial termodinámico para tener en cuenta tanto la energía interna como el trabajo p V en fluidos para sistemas abiertos:

$${\displaystyle \mathrm {d} U_{\mathsf {cv}}=\mathrm {\delta } \,Q+\mathrm {d} H_{\mathsf {in}}-\mathrm {d} H_{\mathsf {out}}-\mathrm {\delta } \,W_{\mathsf {shaft}}~.}$$

Si permitimos también que el límite del sistema se mueva (por ejemplo, debido al movimiento de los pistones), obtenemos una forma bastante general de la primera ley para sistemas abiertos. ^[20] En términos de derivadas de tiempo, utilizando la notación de puntos de Newton para derivadas de tiempo, se lee:

$${\displaystyle {\frac {\mathrm {d} U}{\,\mathrm {d} \,t\,}}=\sum _{k}{\dot {Q}}_{k}+\sum _{k}{\dot {H}}_{k}-\sum _{k}p_{k}{\frac {\,\mathrm {d} V_{k}}{\,\mathrm {d} t\,}}-P\,,}$$

con sumas sobre los distintos lugares k donde se suministra calor, fluye masa hacia el sistema y los límites se mueven. .yo_{Los términos k} representan flujos de entalpía, que pueden escribirse como

$${\displaystyle {\dot {H}}_{k}=h_{k}{\dot {m}}_{k}=H_{\mathsf {m}}{\dot {n}}_{k}\,,}$$

con .metro_k el flujo de masa y .norte_k el flujo molar en la posición k respectivamente. El término ⁠ dVk ​_​ / el  o ⁠ representa la tasa de cambio del volumen del sistema en la posición k que da como resultado p V potencia producida por el sistema. El parámetro P representa todas las demás formas de potencia producidas por el sistema, como la potencia del eje, pero también puede ser, por ejemplo, energía eléctrica producida por una planta de energía eléctrica.

Tenga en cuenta que la expresión anterior es válida solo si se conserva el caudal de energía cinética entre la entrada y la salida del sistema. ^{[ aclaración necesaria ]} De lo contrario, debe incluirse en el balance de entalpía. Durante el funcionamiento en estado estacionario de un dispositivo ( ver turbina , bomba y motor ), el promedio ⁠ tú ​ /el  o⁠ puede establecerse como cero. Esto produce una expresión útil para la generación de energía promedio de estos dispositivos en ausencia de reacciones químicas:

$${\displaystyle P=\sum _{k}\left\langle {\dot {Q}}_{k}\right\rangle +\sum _{k}\left\langle {\dot {H}}_{k}\right\rangle -\sum _{k}\left\langle p_{k}{\frac {\,\mathrm {d} V_{k}}{\,\mathrm {d} t\,}}\right\rangle \,,}$$

donde los corchetes angulares indican promedios temporales. La importancia técnica de la entalpía está directamente relacionada con su presencia en la primera ley para sistemas abiertos, como se formuló anteriormente.

Los valores de entalpía de sustancias importantes se pueden obtener utilizando software comercial. Prácticamente todas las propiedades relevantes de los materiales se pueden obtener en forma de tabla o gráfica. Hay muchos tipos de diagramas, como los diagramas h – T , que dan la entalpía específica como función de la temperatura para varias presiones, y los diagramas h – p , que dan h como función de p para varias T . Uno de los diagramas más comunes es el diagrama de entropía específica de la temperatura ( diagrama T – s ). Da la curva de fusión y los valores de líquido y vapor saturados junto con isobaras e isentalpas. Estos diagramas son herramientas poderosas en manos del ingeniero térmico.

Los puntos  a a h en la figura juegan un papel en la discusión de esta sección.

Punto	yo	pag	s	yo
	K	bar	⁠ kJ / kilogramos kilos ⁠	⁠ kJ / kilogramo ⁠
a	300	1	6.85	461
b	380	2	6.85	530
do	300	200	5.16	430
d	270	1	6,79	430
mi	108	13	3,55	100
F	77.2	1	3,75	100
gramo	77.2	1	2.83	28
yo	77.2	1	5.41	230

Los puntos  e y g son líquidos saturados y el punto  h es un gas saturado.

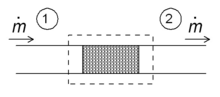
Una de las aplicaciones sencillas del concepto de entalpía es el llamado proceso de estrangulamiento, también conocido como expansión de Joule-Thomson . Se trata de un flujo adiabático constante de un fluido a través de una resistencia al flujo (válvula, tapón poroso o cualquier otro tipo de resistencia al flujo) como se muestra en la figura. Este proceso es muy importante, ya que se encuentra en el corazón de los refrigeradores domésticos , donde es responsable de la caída de temperatura entre la temperatura ambiente y el interior del refrigerador. También es la etapa final en muchos tipos de licuefactores .

Para un régimen de flujo en estado estacionario, la entalpía del sistema (rectángulo punteado) debe ser constante.

$${\displaystyle 0={\dot {m}}h_{1}-{\dot {m}}h_{2}~.}$$

Como el flujo másico es constante, las entalpías específicas en los dos lados de la resistencia al flujo son las mismas:

$${\displaystyle h_{1}=h_{2}\;,}$$

Es decir, la entalpía por unidad de masa no cambia durante la regulación. Las consecuencias de esta relación se pueden demostrar utilizando el diagrama T − s anterior.

El punto  c está a 200 bar y temperatura ambiente (300 K). Una expansión de Joule-Thomson de 200 bar a 1 bar sigue una curva de entalpía constante de aproximadamente 425  ⁠ kJ /kilogramo⁠ (no se muestra en el diagrama) que se encuentra entre los 400 y 450  ⁠ kJ /kilogramo⁠ isentalps y termina en el punto  d , que está a una temperatura de aproximadamente 270 K . Por lo tanto, la expansión de 200 bar a 1 bar enfría el nitrógeno de 300 K a 270 K . En la válvula, hay mucha fricción y se produce mucha entropía, pero aún así la temperatura final está por debajo del valor inicial.

El punto  e se elige de modo que esté en la línea de líquido saturado con h = 100 .  kJ /kilogramo⁠ . Corresponde aproximadamente con p = 13 bar y T = 108 K . La regulación desde este punto hasta una presión de 1 bar termina en la región de dos fases (punto  f ). Esto significa que una mezcla de gas y líquido sale de la válvula de regulación. Dado que la entalpía es un parámetro extensivo, la entalpía en f ( h _f ) es igual a la entalpía en g ( h _g ) multiplicada por la fracción de líquido en f ( x _f ) más la entalpía en h ( h _h ) multiplicada por la fracción de gas en f (1 − x _f ) . Entonces

$${\displaystyle h_{\mathbf {\mathsf {f}} }=x_{\mathbf {\mathsf {f}} }h_{\mathbf {\mathsf {g}} }+(1-x_{\mathbf {\mathsf {f}} })h_{\mathsf {\mathbf {h} }}~.}$$

Con números:

100 = x _f × 28 + ( 1 − x _f ) × 230 , entonces x _f = 0,64 .

Esto significa que la fracción de masa del líquido en la mezcla líquido-gas que sale de la válvula de estrangulamiento es del 64%.

Se aplica una potencia P, por ejemplo, como potencia eléctrica. Si la compresión es adiabática , la temperatura del gas aumenta. En el caso reversible, estaría a entropía constante, lo que corresponde con una línea vertical en el diagrama T – s . Por ejemplo, comprimir nitrógeno de 1 bar (punto a ) a 2 bar (punto b ) daría como resultado un aumento de temperatura de 300 K a 380 K. Para que el gas comprimido salga a temperatura ambiente T _a , es necesario un intercambio de calor, por ejemplo, mediante agua de refrigeración. En el caso ideal, la compresión es isotérmica. El flujo de calor promedio hacia los alrededores es Q̇ . Dado que el sistema está en estado estacionario, la primera ley da

$${\displaystyle 0=-{\dot {Q}}+{\dot {m}}\,h_{1}-{\dot {m}}\,h_{2}+P~.}$$

La potencia mínima necesaria para la compresión se obtiene si la compresión es reversible. En ese caso, la segunda ley de la termodinámica para sistemas abiertos da

$${\displaystyle 0=-{\frac {\,{\dot {Q}}\,}{T_{\mathsf {a}}}}+{\dot {m}}\,s_{1}-{\dot {m}}\,s_{2}~.}$$

La eliminación de Q̇ da como resultado la potencia mínima

$${\displaystyle {\frac {\,P_{\mathsf {min}}\,}{\dot {m}}}=h_{2}-h_{1}-T_{\mathsf {a}}\left(s_{2}-s_{1}\right)~.}$$

Por ejemplo, comprimir 1 kg de nitrógeno de 1 bar a 200 bar cuesta al menos: ( h _c − h _a ) − T _a ( s _c − s _a ) . Con los datos, obtenidos con el diagrama T – s , encontramos un valor de (430 − 461) − 300 × (5,16 − 6,85) = 476 ⁠  kJ /kilogramo⁠ .

La relación de potencia se puede simplificar aún más escribiéndola como

$${\displaystyle {\frac {\,P_{\mathsf {min}}\,}{\dot {m}}}=\int _{1}^{2}\left(\mathrm {d} h-T_{\mathsf {a}}\,\mathrm {d} s\right)~.}$$

Con

d h = T  d s + v  d p ,

Esto da como resultado la relación final

$${\displaystyle {\frac {\,P_{\mathsf {min}}}{\dot {m}}}=\int _{1}^{2}v\,\mathrm {d} p~.}$$

El término entalpía fue acuñado relativamente tarde en la historia de la termodinámica, a principios del siglo XX. El término energía fue introducido en un sentido moderno por Thomas Young en 1802, mientras que el término entropía fue introducido por Rudolf Clausius en 1865. Energía utiliza la raíz de la palabra griega ἔργον ( ergon ), que significa "trabajo", ^[22] para expresar la idea de capacidad para realizar trabajo. Entropía utiliza la palabra griega τροπή ( tropē ), que significa transformación o giro . ^[23] Entalpía utiliza la raíz de la palabra griega θάλπος ( thalpos ), "calor, calidez". ^[24]

El término expresa el concepto obsoleto de contenido de calor , ^{[nota 2]} ya que d H se refiere a la cantidad de calor ganado en un proceso a presión constante solamente, ^[25] pero no en el caso general cuando la presión es variable. ^[18] JW Gibbs utilizó el término "una función de calor para presión constante" para mayor claridad. ^{[nota 3]}

La introducción del concepto de "contenido calorífico" H está asociada con Benoît Paul Émile Clapeyron y Rudolf Clausius ( relación Clausius-Clapeyron , 1850).

El término entalpía apareció impreso por primera vez en 1909. ^[28] Se atribuye a Heike Kamerlingh Onnes , quien probablemente lo introdujo oralmente el año anterior, en la primera reunión del Instituto de Refrigeración en París. ^[29] Ganó popularidad recién en la década de 1920, en particular con las Tablas y diagramas de vapor de Mollier , publicadas en 1927.

Hasta la década de 1920, el símbolo H se utilizaba, de forma un tanto inconsistente, para designar el "calor" en general. La definición de H como estrictamente limitada a la entalpía o "contenido de calor a presión constante" fue propuesta formalmente por A. W. Porter en 1922. ^{[30] [31]}

• Weisstein, Eric. "Entalpía". El mundo de la física de Eric Weisstein – vía scienceworld.wolfram.com.
• "Entalpía". Hipertexto sobre termodinámica. Departamento de Física y Astronomía. Universidad Estatal de Georgia .
• "Ejemplos de cálculos de entalpía" (notas del tutorial). Departamento de Química. Universidad Texas A&M . Archivado desde el original el 10 de octubre de 2006.