Proceso isotérmico

Termodinámica
La clásica máquina térmica de Carnot
Sucursales Clásico Estadístico Químico Termodinámica cuántica Equilibrio  / No equilibrio
Leyes Cero Primero Segundo Tercero
Sistemas Sistema cerrado Sistema abierto Sistema aislado Estado Ecuación de estado Gas ideal Gas real Estado de la materia Fase (materia) Equilibrio Controlar el volumen Instrumentos Procesos Isobárico Isocórico Isotermal Adiabático Isentrópico Isentálpico Cuasistático Politrópico Expansión libre Reversibilidad Irreversibilidad Endorreversibilidad Ciclos Motores térmicos Bombas de calor Eficiencia térmica
Propiedades del sistema Nota: Variables conjugadas en cursiva Diagramas de propiedades Propiedades intensivas y extensivas Funciones del proceso Trabajar Calor Funciones del estado Temperatura  / Entropía  ( introducción ) Presión  / Volumen Potencial químico  / Número de partículas Calidad del vapor Propiedades reducidas
Propiedades del material Bases de datos de propiedades Capacidad calorífica específica  ${\estilo de visualización c=}$ ${\estilo de visualización T}$ ${\displaystyle \s parcial}$ ${\estilo de visualización N}$ ${\displaystyle \parcial T}$ Compresibilidad  ${\displaystyle \beta =-}$ ${\estilo de visualización 1}$ ${\displaystyle \V parcial}$ ${\estilo de visualización V}$ ${\displaystyle \p parcial}$ Expansión térmica  ${\displaystyle \alpha =}$ ${\estilo de visualización 1}$ ${\displaystyle \V parcial}$ ${\estilo de visualización V}$ ${\displaystyle \parcial T}$
Ecuaciones Teorema de Carnot Teorema de Clausius Relación fundamental Ley de los gases ideales Relaciones de Maxwell Relaciones recíprocas de Onsager Ecuaciones de Bridgman Tabla de ecuaciones termodinámicas
Potenciales Energía libre Entropía libre Energía interna ${\displaystyle U(S,V)}$ Entalpía ${\displaystyle H(S,p)=U+pV}$ Energía libre de Helmholtz ${\displaystyle A(T,V)=U-TS}$ Energía libre de Gibbs ${\displaystyle G(T,p)=H-TS}$
Historia Cultura Historia General Entropía Leyes de los gases Máquinas de "movimiento perpetuo" Filosofía Entropía y tiempo Entropía y vida Trinquete browniano El demonio de Maxwell Paradoja de la muerte por calor La paradoja de Loschmidt Sinergética Teorías Teoría calórica Vis viva ("fuerza viva") Equivalente mecánico del calor Fuerza motriz Publicaciones clave Una investigación sobre la fuente... Fricción Sobre el equilibrio de sustancias heterogéneas Reflexiones sobre la fuerza motriz del fuego Líneas de tiempo Termodinámica Motores térmicos Arte Educación Superficie termodinámica de Maxwell La entropía como dispersión de energía
Científicos Bernoulli Boltzman Hombre bridgman Caratheodory Carnot Clapeyron Clausio De Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

Un proceso isotérmico es un tipo de proceso termodinámico en el que la temperatura T de un sistema permanece constante: Δ T  = 0. Esto ocurre típicamente cuando un sistema está en contacto con un depósito térmico externo y se produce un cambio en el sistema lo suficientemente lento como para permitir que el sistema se ajuste continuamente a la temperatura del depósito a través del intercambio de calor (ver cuasiequilibrio ). Por el contrario, un proceso adiabático es donde un sistema no intercambia calor con sus alrededores ( Q  = 0).

De manera sencilla, podemos decir que en un proceso isotérmico

• ${\displaystyle T={\text{constant}}}$
• ${\displaystyle \Delta T=0}$
• ${\displaystyle dT=0}$
• Sólo para gases ideales , energía interna ${\displaystyle \Delta U=0}$

Mientras que en los procesos adiabáticos:

• ${\displaystyle Q=0.}$

El sustantivo isoterma se deriva de las palabras griegas antiguas ἴσος ( ísos ), que significa "igual", y θέρμη ( thérmē ), que significa "calor".

Los procesos isotérmicos pueden ocurrir en cualquier tipo de sistema que tenga algún medio de regular la temperatura, incluyendo máquinas altamente estructuradas , e incluso células vivas . Algunas partes de los ciclos de algunas máquinas térmicas se llevan a cabo de forma isotérmica (por ejemplo, en el ciclo de Carnot ). ^[1] En el análisis termodinámico de las reacciones químicas , es habitual analizar primero lo que ocurre en condiciones isotérmicas y luego considerar el efecto de la temperatura. ^[2] Los cambios de fase , como la fusión o la evaporación , también son procesos isotérmicos cuando, como suele ser el caso, ocurren a presión constante. ^[3] Los procesos isotérmicos se utilizan a menudo como punto de partida para analizar procesos más complejos, no isotérmicos.

Los procesos isotérmicos son de especial interés para los gases ideales. Esto es una consecuencia de la segunda ley de Joule , que establece que la energía interna de una cantidad fija de un gas ideal depende únicamente de su temperatura. ^[4] Por lo tanto, en un proceso isotérmico, la energía interna de un gas ideal es constante. Esto es resultado del hecho de que en un gas ideal no hay fuerzas intermoleculares . ^[4] Nótese que esto es cierto únicamente para los gases ideales; la energía interna depende de la presión así como de la temperatura para líquidos, sólidos y gases reales. ^[5]

En la compresión isotérmica de un gas se realiza trabajo sobre el sistema para disminuir el volumen y aumentar la presión. ^[4] Realizar trabajo sobre el gas aumenta la energía interna y tenderá a aumentar la temperatura. Para mantener la temperatura constante, la energía debe salir del sistema en forma de calor y entrar al ambiente. Si el gas es ideal, la cantidad de energía que entra al ambiente es igual al trabajo realizado sobre el gas, porque la energía interna no cambia. Para la expansión isotérmica, la energía suministrada al sistema realiza trabajo sobre los alrededores. En cualquier caso, con la ayuda de un enlace adecuado, el cambio en el volumen del gas puede realizar trabajo mecánico útil. Para obtener detalles de los cálculos, consulte cálculo del trabajo.

En el caso de un proceso adiabático , en el que no fluye calor hacia dentro o hacia fuera del gas porque su recipiente está bien aislado, Q  = 0. Si tampoco se realiza trabajo, es decir, hay una expansión libre , no hay cambio en la energía interna. En el caso de un gas ideal, esto significa que el proceso también es isotérmico. ^[4] Por lo tanto, especificar que un proceso es isotérmico no es suficiente para especificar un proceso único.

En el caso especial de un gas al que se aplica la ley de Boyle ^[4] , el producto pV ( p para la presión del gas y V para el volumen del gas) es una constante si el gas se mantiene en condiciones isotérmicas. El valor de la constante es nRT , donde n es el número de moles del gas presente y R es la constante del gas ideal . En otras palabras, se aplica la ley de los gases ideales pV  =  nRT . ^[4] Por lo tanto:

${\displaystyle p={nRT \over V}={{\text{constant}} \over V}}$

La familia de curvas generadas por esta ecuación se muestra en el gráfico de la Figura 1. Cada curva se denomina isoterma, es decir, una curva a una misma temperatura T. Estos gráficos se denominan diagramas indicadores y fueron utilizados por primera vez por James Watt y otros para controlar la eficiencia de los motores. La temperatura correspondiente a cada curva de la figura aumenta desde la parte inferior izquierda hasta la parte superior derecha.

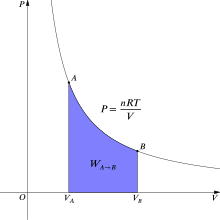
En termodinámica, el trabajo reversible involucrado cuando un gas cambia del estado A al estado B es ^[6]

${\displaystyle W_{A\to B}=-\int _{V_{A}}^{V_{B}}p\,dV}$

donde p es la presión del gas y V el volumen del gas. Para un proceso isotérmico (temperatura constante T ), reversible , esta integral es igual al área bajo la isoterma PV (presión-volumen) relevante, y se indica en violeta en la Figura 2 para un gas ideal. Nuevamente, p  =  ⁠nRT/V⁠ se aplica y siendo T constante (ya que este es un proceso isotérmico), la expresión para el trabajo se convierte en:

${\displaystyle W_{A\to B}=-\int _{V_{A}}^{V_{B}}p\,dV=-\int _{V_{A}}^{V_{B}}{\frac {nRT}{V}}dV=-nRT\int _{V_{A}}^{V_{B}}{\frac {1}{V}}dV=-nRT\ln {\frac {V_{B}}{V_{A}}}}$

En la convención IUPAC , el trabajo se define como el trabajo que el entorno realiza sobre un sistema. Si, por ejemplo, el sistema está comprimido, el trabajo lo realiza el entorno, por lo que el trabajo es positivo y la energía interna del sistema aumenta. Por el contrario, si el sistema se expande (es decir, el entorno del sistema se expande, por lo que no se trata de expansiones libres ), entonces el trabajo es negativo, ya que el sistema realiza trabajo sobre el entorno y la energía interna del sistema disminuye.

También vale la pena señalar que para los gases ideales, si la temperatura se mantiene constante, la energía interna del sistema U también es constante, y por lo tanto Δ U  = 0. Dado que la Primera Ley de la Termodinámica establece que Δ U  =  Q  +  W en la convención IUPAC , se deduce que Q  = − W para la compresión o expansión isotérmica de los gases ideales.

La expansión reversible de un gas ideal puede utilizarse como ejemplo del trabajo producido por un proceso isotérmico. Es de particular interés el grado en que el calor se convierte en trabajo utilizable y la relación entre la fuerza de confinamiento y el grado de expansión.

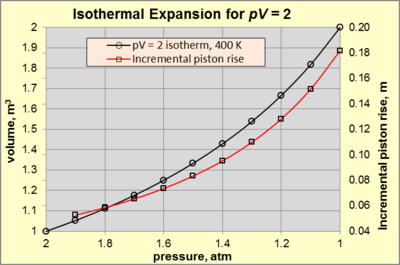
Durante la expansión isotérmica de un gas ideal, tanto p como V cambian a lo largo de una isoterma con un producto pV constante (es decir, T constante ). Considere un gas de trabajo en una cámara cilíndrica de 1 m de alto y 1 m ² de área (es decir, 1 m ³ de volumen) a 400 K en equilibrio estático . Los alrededores consisten en aire a 300 K y 1 atm de presión (designado como p _surr ). El gas de trabajo está confinado por un pistón conectado a un dispositivo mecánico que ejerce una fuerza suficiente para crear una presión de gas de trabajo de 2 atm (estado A ). Para cualquier cambio en el estado A que cause una disminución de la fuerza, el gas se expandirá y realizará trabajo sobre los alrededores. La expansión isotérmica continúa mientras la fuerza aplicada disminuya y se agregue el calor apropiado para mantener pV = 2 [atm·m ³ ] (= 2 atm × 1 m ³ ). Se dice que la expansión es internamente reversible si el movimiento del pistón es suficientemente lento como para que en cada instante durante la expansión la temperatura y la presión del gas sean uniformes y se ajusten a la ley de los gases ideales . La figura 3 muestra la relación p – V para pV = 2 [atm·m ³ ] para una expansión isotérmica de 2 atm (estado A ) a 1 atm (estado B ).

El trabajo realizado (designado ) tiene dos componentes. En primer lugar, el trabajo de expansión contra la presión atmosférica circundante (designado como W _{p Δ V} ), y en segundo lugar, el trabajo mecánico utilizable (designado como W _mech ). La salida W _mech aquí podría ser el movimiento del pistón utilizado para girar un brazo de manivela, que luego haría girar una polea capaz de sacar agua de minas de sal inundadas .${\displaystyle W_{A\to B}}$

${\displaystyle W_{A\to B}=-p\,V\left(\ln {\frac {V_{B}}{V_{A}}}\right)=-W_{p\Delta V}-W_{\rm {mech}}}$

El sistema alcanza el estado B ( pV = 2 [atm·m ³ ] con p = 1 atm y V = 2 m ³ ) cuando la fuerza aplicada llega a cero. En ese punto, es igual a –140,5 kJ, y W _{p Δ V} es –101,3 kJ. Por diferencia, W _mech = –39,1 kJ, que es el 27,9% del calor suministrado al proceso (- 39,1 kJ / - 140,5 kJ). Esta es la cantidad máxima de trabajo mecánico utilizable que se puede obtener del proceso en las condiciones establecidas. El porcentaje de W _mech es una función de pV y p _surr , y se acerca al 100% cuando p _surr se acerca a cero.${\displaystyle W_{A\to B}}$

Para estudiar más a fondo la naturaleza de la expansión isotérmica, observe la línea roja en la Figura 3. El valor fijo de pV provoca un aumento exponencial en la elevación del pistón frente a la disminución de la presión. Por ejemplo, una disminución de la presión de 2 a 1,9 atm provoca una elevación del pistón de 0,0526 m. En comparación, una disminución de la presión de 1,1 a 1 atm provoca una elevación del pistón de 0,1818 m.

Los procesos isotérmicos son especialmente convenientes para calcular cambios en la entropía ya que, en este caso, la fórmula para el cambio de entropía, Δ S , es simplemente

${\displaystyle \Delta S={\frac {Q_{\text{rev}}}{T}}}$

donde Q _rev es el calor transferido (internamente reversible) al sistema y T es la temperatura absoluta . ^[7] Esta fórmula es válida sólo para un proceso reversible hipotético ; es decir, un proceso en el que el equilibrio se mantiene en todo momento.

Un ejemplo sencillo es una transición de fase de equilibrio (como la fusión o la evaporación) que se produce a temperatura y presión constantes. Para una transición de fase a presión constante, el calor transferido al sistema es igual a la entalpía de transformación , Δ H _tr , por lo tanto Q  = Δ H _tr . ^[3] A cualquier presión dada, habrá una temperatura de transición, T _tr , para la cual las dos fases están en equilibrio (por ejemplo, el punto de ebullición normal para la vaporización de un líquido a una presión de una atmósfera). Si la transición se produce en tales condiciones de equilibrio, la fórmula anterior puede utilizarse para calcular directamente el cambio de entropía ^[7]

${\displaystyle \Delta S_{\text{tr}}={\frac {\Delta H_{\text{tr}}}{T_{\text{tr}}}}}$.

Otro ejemplo es la expansión isotérmica reversible (o compresión) de un gas ideal desde un volumen inicial V _A y una presión P _A hasta un volumen final V _B y una presión P _B . Como se muestra en el Cálculo del trabajo, el calor transferido al gas es

${\displaystyle Q=-W=nRT\ln {\frac {V_{\text{B}}}{V_{\text{A}}}}}$.

Este resultado es para un proceso reversible, por lo que se puede sustituir en la fórmula del cambio de entropía para obtener ^[7].

${\displaystyle \Delta S=nR\ln {\frac {V_{\text{B}}}{V_{\text{A}}}}}$.

Dado que un gas ideal obedece la Ley de Boyle , esto se puede reescribir, si se desea, como

${\displaystyle \Delta S=nR\ln {\frac {P_{\text{A}}}{P_{\text{B}}}}}$.

Una vez obtenidas, estas fórmulas se pueden aplicar a un proceso irreversible , como la expansión libre de un gas ideal. Dicha expansión también es isotérmica y puede tener los mismos estados inicial y final que en la expansión reversible. Dado que la entropía es una función de estado (que depende de un estado de equilibrio, no de un camino que el sistema toma para alcanzar ese estado), el cambio en la entropía del sistema es el mismo que en el proceso reversible y se da por las fórmulas anteriores. Nótese que el resultado Q  = 0 para la expansión libre no se puede utilizar en la fórmula para el cambio de entropía ya que el proceso no es reversible.

La diferencia entre lo reversible y lo irreversible se encuentra en la entropía del entorno. En ambos casos, el entorno está a temperatura constante, T , por lo que Δ S _sur  = − ⁠Q/yo⁠ ; se utiliza el signo menos ya que el calor transferido al entorno es igual en magnitud y opuesto en signo al calor Q transferido al sistema. En el caso reversible, el cambio de entropía del entorno es igual y opuesto al cambio en el sistema, por lo que el cambio de entropía del universo es cero. En el irreversible, Q  = 0, por lo que la entropía del entorno no cambia y el cambio de entropía del universo es igual a ΔS para el sistema.

• Efecto Joule-Thomson
• Expansión de Joule (también llamada expansión libre )
• Proceso adiabático
• Proceso cíclico
• Proceso isobárico
• Proceso isocórico
• Proceso politrópico
• Proceso espontáneo