Segunda ley de la termodinámica

Termodinámica
La clásica máquina térmica de Carnot
Sucursales Clásico Estadístico Químico Termodinámica cuántica Equilibrio  / No equilibrio
Leyes Cero Primero Segundo Tercero
Sistemas Sistema cerrado Sistema abierto Sistema aislado Estado Ecuación de estado Gas ideal Gas real Estado de la materia Fase (materia) Equilibrio Controlar el volumen Instrumentos Procesos Isobárico Isocórico Isotermal Adiabático Isentrópico Isentálpico Cuasistático Politrópico Free expansion Reversibility Irreversibility Endoreversibility Cycles Heat engines Heat pumps Thermal efficiency
System properties Note: Conjugate variables in italics Property diagrams Intensive and extensive properties Process functions Work Heat Functions of state Temperature / Entropy (introduction) Pressure / Volume Chemical potential / Particle number Vapor quality Reduced properties
Material properties Property databases Specific heat capacity  ${\displaystyle c=}$ ${\displaystyle T}$ ${\displaystyle \partial S}$ ${\displaystyle N}$ ${\displaystyle \partial T}$ Compressibility  ${\displaystyle \beta =-}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial p}$ Thermal expansion  ${\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial T}$
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Onsager reciprocal relations Bridgman's equations Table of thermodynamic equations
Potentials Free energy Free entropy Internal energy ${\displaystyle U(S,V)}$ Enthalpy ${\displaystyle H(S,p)=U+pV}$ Helmholtz free energy ${\displaystyle A(T,V)=U-TS}$ Gibbs free energy ${\displaystyle G(T,p)=H-TS}$
History Culture History General Entropy Gas laws "Perpetual motion" machines Philosophy Entropy and time Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics Theories Caloric theory Vis viva ("living force") Mechanical equivalent of heat Motive power Key publications An Inquiry Concerning the Source ... Friction On the Equilibrium of Heterogeneous Substances Reflections on the Motive Power of Fire Timelines Thermodynamics Heat engines Art Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Boltzmann Bridgman Carathéodory Carnot Clapeyron Clausius de Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

La segunda ley de la termodinámica es una ley física basada en la observación empírica universal sobre las interconversiones de calor y energía . Una afirmación simple de la ley es que el calor siempre fluye espontáneamente desde las regiones más calientes a las más frías de la materia (o "cuesta abajo" en términos del gradiente de temperatura). Otra afirmación es: "No todo el calor se puede convertir en trabajo en un proceso cíclico ". ^{[1] [2] [3]}

La segunda ley de la termodinámica establece el concepto de entropía como una propiedad física de un sistema termodinámico . Predice si los procesos están prohibidos a pesar de obedecer el requisito de conservación de la energía expresado en la primera ley de la termodinámica y proporciona los criterios necesarios para los procesos espontáneos . Por ejemplo, la primera ley permite el proceso de una taza que se cae de una mesa y se rompe en el suelo, así como el proceso inverso de los fragmentos de la taza que se vuelven a unir y "saltan" de nuevo a la mesa, mientras que la segunda ley permite el primero y niega el segundo. La segunda ley puede formularse mediante la observación de que la entropía de los sistemas aislados dejados a la evolución espontánea no puede disminuir, ya que siempre tienden hacia un estado de equilibrio termodinámico donde la entropía es máxima en la energía interna dada. ^[4] Un aumento en la entropía combinada del sistema y el entorno explica la irreversibilidad de los procesos naturales, a menudo mencionada en el concepto de la flecha del tiempo . ^{[5] [6]}

Históricamente, la segunda ley fue un hallazgo empírico que se aceptó como un axioma de la teoría termodinámica . La mecánica estadística proporciona una explicación microscópica de la ley en términos de distribuciones de probabilidad de los estados de grandes conjuntos de átomos o moléculas . La segunda ley se ha expresado de muchas maneras. Su primera formulación, que precedió a la definición adecuada de entropía y se basó en la teoría calórica , es el teorema de Carnot , formulado por el científico francés Sadi Carnot , quien en 1824 demostró que la eficiencia de conversión de calor en trabajo en un motor térmico tiene un límite superior. ^{[7] [8]} La primera definición rigurosa de la segunda ley basada en el concepto de entropía provino del científico alemán Rudolf Clausius en la década de 1850 e incluyó su afirmación de que el calor nunca puede pasar de un cuerpo más frío a uno más cálido sin que algún otro cambio, conectado con él, ocurra al mismo tiempo.

La segunda ley de la termodinámica permite definir el concepto de temperatura termodinámica , pero ésta ha sido delegada formalmente a la ley cero de la termodinámica .

La primera ley de la termodinámica proporciona la definición de la energía interna de un sistema termodinámico y expresa su cambio para un sistema cerrado en términos de trabajo y calor . ^[9] Puede vincularse con la ley de conservación de la energía . ^[10] Conceptualmente, la primera ley describe el principio fundamental de que los sistemas no consumen ni "agotan" energía, que la energía no se crea ni se destruye, sino que simplemente se convierte de una forma a otra.

La segunda ley se ocupa de la dirección de los procesos naturales. ^[11] Afirma que un proceso natural se desarrolla sólo en un sentido y no es reversible. Es decir, el estado de un sistema natural en sí mismo puede revertirse, pero no sin aumentar la entropía del entorno del sistema, es decir, tanto el estado del sistema como el estado de su entorno no pueden revertirse juntos, por completo, sin implicar la destrucción de la entropía.

Por ejemplo, cuando se crea un camino para la conducción o la radiación , el calor siempre fluye espontáneamente de un cuerpo más caliente a uno más frío. Estos fenómenos se explican en términos de cambio de entropía . ^{[12] [13]} Una bomba de calor puede invertir este flujo de calor, pero tanto el proceso de inversión como el proceso original provocan la producción de entropía, lo que aumenta la entropía de los alrededores del sistema. Si un sistema aislado que contiene subsistemas distintos se mantiene inicialmente en equilibrio termodinámico interno mediante particiones internas mediante paredes impermeables entre los subsistemas, y luego alguna operación hace que las paredes sean más permeables, entonces el sistema evoluciona espontáneamente para alcanzar un nuevo equilibrio termodinámico interno final , y su entropía total, , aumenta.${\displaystyle S}$

En un proceso idealizado, reversible o cuasiestático , de transferencia de energía en forma de calor a un sistema termodinámico cerrado de interés (que permite la entrada o salida de energía, pero no la transferencia de materia), desde un sistema termodinámico auxiliar, se define que un incremento infinitesimal ( ) en la entropía del sistema de interés resulta de una transferencia infinitesimal de calor ( ) al sistema de interés, dividida por la temperatura termodinámica común del sistema de interés y el sistema termodinámico auxiliar: ^[14]${\displaystyle \mathrm {d} S}$${\displaystyle \delta Q}$ ${\displaystyle (T)}$

${\displaystyle \mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; idealized, reversible process)}}.}$

Se utilizan notaciones diferentes para una cantidad infinitesimal de calor y un cambio infinitesimal de entropía porque la entropía es una función del estado , mientras que el calor, como el trabajo, no lo es.${\displaystyle (\delta )}$${\displaystyle (\mathrm {d} )}$

Para un proceso infinitesimal realmente posible sin intercambio de masa con el entorno, la segunda ley requiere que el incremento de la entropía del sistema cumpla la desigualdad ^{[15] [16]}

${\displaystyle \mathrm {d} S>{\frac {\delta Q}{T_{\text{surr}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; actually possible, irreversible process).}}}$

Esto se debe a que un proceso general para este caso (sin intercambio de masa entre el sistema y sus alrededores) puede incluir trabajo realizado sobre el sistema por sus alrededores, lo que puede tener efectos de fricción o viscosos dentro del sistema, porque puede estar en curso una reacción química o porque la transferencia de calor en realidad ocurre solo de manera irreversible, impulsada por una diferencia finita entre la temperatura del sistema ( T ) y la temperatura de los alrededores ( T _surr ). ^{[17] [18]}

La igualdad todavía se aplica para el flujo de calor puro (solo flujo de calor, sin cambios en la composición química y la masa),

${\displaystyle \mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(actually possible quasistatic irreversible process without composition change).}}}$

que es la base para la determinación precisa de la entropía absoluta de sustancias puras a partir de curvas de capacidad térmica medidas y cambios de entropía en transiciones de fase, es decir, por calorimetría. ^{[19] [15]}

Introduciendo un conjunto de variables internas para describir la desviación de un sistema termodinámico de un estado de equilibrio químico en equilibrio físico (con la presión uniforme P y la temperatura T bien definidas requeridas ), se puede registrar la igualdad${\displaystyle \xi }$

${\displaystyle \mathrm {d} S={\frac {\delta Q}{T}}-{\frac {1}{T}}\sum _{j}\,\Xi _{j}\,\delta \xi _{j}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; actually possible quasistatic irreversible process).}}}$

El segundo término representa el trabajo de las variables internas que pueden verse perturbadas por influencias externas, pero el sistema no puede realizar ningún trabajo positivo a través de las variables internas. Esta afirmación introduce la imposibilidad de la reversión de la evolución del sistema termodinámico en el tiempo y puede considerarse como una formulación del segundo principio de la termodinámica , la formulación que, por supuesto, es equivalente a la formulación del principio en términos de entropía. ^{[20] [21]}

La ley cero de la termodinámica, en su forma habitual y breve, permite reconocer que dos cuerpos en una relación de equilibrio térmico tienen la misma temperatura, especialmente que un cuerpo de prueba tiene la misma temperatura que un cuerpo termométrico de referencia. ^[22] Para un cuerpo en equilibrio térmico con otro, existen infinitas escalas de temperatura empíricas, que en general dependen respectivamente de las propiedades de un cuerpo termométrico de referencia particular. La segunda ley permite ^{[ aclaración necesaria ] una escala de temperatura distinguida, que define una} temperatura termodinámica absoluta , independiente de las propiedades de cualquier cuerpo termométrico de referencia particular. ^{[23] [24]}

La segunda ley de la termodinámica puede expresarse de muchas maneras específicas ^[25] , siendo las afirmaciones clásicas más destacadas ^[26] la de Rudolf Clausius (1854), la de Lord Kelvin (1851) y la de Constantin Carathéodory (1909) en termodinámica axiomática . Estas afirmaciones expresan la ley en términos físicos generales y citan la imposibilidad de ciertos procesos. Se ha demostrado que las afirmaciones de Clausius y Kelvin son equivalentes ^{[27] .}

El origen histórico ^[28] de la segunda ley de la termodinámica se encuentra en el análisis teórico de Sadi Carnot sobre el flujo de calor en las máquinas de vapor (1824). La pieza central de ese análisis, ahora conocida como máquina de Carnot , es una máquina térmica ideal que funciona ficticiamente en el modo límite de extrema lentitud conocido como cuasiestático, de modo que las transferencias de calor y trabajo se dan entre subsistemas que siempre están en sus propios estados internos de equilibrio termodinámico . Representa la máxima eficiencia teórica de una máquina térmica que funciona entre dos depósitos térmicos o de calor cualesquiera a diferentes temperaturas. El principio de Carnot fue reconocido por Carnot en una época en la que la teoría calórica representaba la comprensión dominante de la naturaleza del calor, antes del reconocimiento de la primera ley de la termodinámica y antes de la expresión matemática del concepto de entropía. Interpretado a la luz de la primera ley, el análisis de Carnot es físicamente equivalente a la segunda ley de la termodinámica y sigue siendo válido en la actualidad. Algunas muestras de su libro son:

... dondequiera que exista una diferencia de temperatura, se puede producir fuerza motriz. ^[29]

La producción de fuerza motriz se debe entonces en las máquinas de vapor no a un consumo real de calorías, sino a su transporte desde un cuerpo caliente a un cuerpo frío... ^[30]

La fuerza motriz del calor es independiente de los agentes empleados para realizarlo; su cantidad está fijada únicamente por las temperaturas de los cuerpos entre los cuales se efectúa, finalmente, la transferencia de calórico. ^[31]

En términos modernos, el principio de Carnot puede enunciarse con mayor precisión:

La eficiencia de un ciclo de Carnot cuasiestático o reversible depende únicamente de las temperaturas de los dos depósitos de calor y es la misma, independientemente de la sustancia activa. Un motor de Carnot operado de esta manera es el motor térmico más eficiente posible utilizando esas dos temperaturas. ^{[32] [33] [34] [35] [36] [37]}

El científico alemán Rudolf Clausius sentó las bases de la segunda ley de la termodinámica en 1850 al examinar la relación entre la transferencia de calor y el trabajo. ^[38] Su formulación de la segunda ley, que se publicó en alemán en 1854, se conoce como la declaración de Clausius :

El calor nunca puede pasar de un cuerpo más frío a uno más caliente sin que se produzca al mismo tiempo algún otro cambio relacionado con él. ^[39]

La afirmación de Clausius utiliza el concepto de "transferencia de calor". Como es habitual en los debates sobre termodinámica, esto significa "transferencia neta de energía en forma de calor" y no se refiere a transferencias contributivas en un sentido u otro.

El calor no puede fluir espontáneamente de las regiones frías a las calientes sin que se realice un trabajo externo sobre el sistema, lo que resulta evidente a partir de la experiencia ordinaria de la refrigeración , por ejemplo. En un refrigerador, el calor se transfiere del frío al calor, pero solo cuando lo fuerza un agente externo, el sistema de refrigeración.

Lord Kelvin expresó la segunda ley en varias palabras.

Es imposible que una máquina autónoma, sin ayuda de ningún agente externo, transmita calor de un cuerpo a otro a una temperatura más alta.

Es imposible, por medio de la acción de materiales inanimados, derivar un efecto mecánico de cualquier porción de materia enfriándola por debajo de la temperatura del más frío de los objetos circundantes. ^[40]

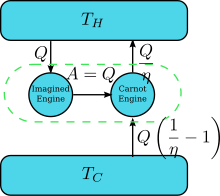
Supongamos que hay un motor que viola el enunciado de Kelvin: es decir, uno que drena calor y lo convierte completamente en trabajo (el calor drenado se convierte completamente en trabajo) de manera cíclica sin ningún otro resultado. Ahora emparejemoslo con un motor de Carnot invertido como se muestra en la figura de la derecha. La eficiencia de un motor térmico normal es η y, por lo tanto, la eficiencia del motor térmico invertido es 1/ η . El efecto neto y único del par combinado de motores es transferir calor del depósito más frío al más caliente, lo que viola el enunciado de Clausius. Esto es una consecuencia de la primera ley de la termodinámica , en cuanto a que la energía del sistema total permanezca igual; , por lo tanto , donde (1) se utiliza la convención de signos del calor en la que el calor que entra (sale) de un motor es positivo (negativo) y (2) se obtiene por la definición de eficiencia del motor cuando el funcionamiento del motor no se invierte. Por lo tanto, una violación del enunciado de Kelvin implica una violación del enunciado de Clausius, es decir, el enunciado de Clausius implica el enunciado de Kelvin. Podemos demostrar de manera similar que el enunciado de Kelvin implica el enunciado de Clausius y, por lo tanto, ambos son equivalentes.${\textstyle \Delta Q=Q\left({\frac {1}{\eta }}-1\right)}$${\textstyle {\text{Input}}+{\text{Output}}=0\implies (Q+Q_{c})-{\frac {Q}{\eta }}=0}$${\textstyle Q_{c}=Q\left({\frac {1}{\eta }}-1\right)}$${\displaystyle {\frac {Q}{\eta }}}$

Planck propuso la siguiente proposición, derivada directamente de la experiencia. A veces se la considera su enunciado de la segunda ley, pero él la consideró un punto de partida para la derivación de la segunda ley.

Es imposible construir un motor que funcione en un ciclo completo y no produzca ningún efecto excepto la producción de trabajo y el enfriamiento de un depósito de calor. ^{[41] [42]}

Es casi habitual en los libros de texto hablar del "enunciado de Kelvin-Planck" de la ley, como por ejemplo en el texto de ter Haar y Wergeland . ^[43] Esta versión, también conocida como el enunciado del motor térmico , de la segunda ley establece que

Es imposible idear un dispositivo que funcione cíclicamente , cuyo único efecto sea absorber energía en forma de calor de un único depósito térmico y entregar una cantidad equivalente de trabajo . ^[2]

Max Planck enunció la segunda ley de la siguiente manera.

Todo proceso que ocurre en la naturaleza se produce en el sentido de que la suma de las entropías de todos los cuerpos que participan en el proceso aumenta. En el límite, es decir, en los procesos reversibles, la suma de las entropías permanece invariable. ^{[44] [45] [46]}

Un planteamiento muy parecido al de Planck es el de George Uhlenbeck y G. W. Ford para los fenómenos irreversibles .

... en un cambio irreversible o espontáneo de un estado de equilibrio a otro (como por ejemplo la igualación de temperatura de dos cuerpos A y B, cuando se ponen en contacto) la entropía siempre aumenta. ^[47]

Constantin Carathéodory formuló la termodinámica sobre una base axiomática puramente matemática. Su enunciado de la segunda ley se conoce como el Principio de Carathéodory, que puede formularse de la siguiente manera: ^[48]

En cada vecindad de cualquier estado S de un sistema adiabáticamente cerrado hay estados inaccesibles desde S. ^[49]

Con esta formulación, describió por primera vez el concepto de accesibilidad adiabática y sentó las bases para un nuevo subcampo de la termodinámica clásica, a menudo llamada termodinámica geométrica . Del principio de Carathéodory se desprende que la cantidad de energía transferida cuasiestáticamente como calor es una función de proceso holonómica , en otras palabras, . ^[50]${\displaystyle \delta Q=TdS}$

Aunque en los libros de texto es casi habitual decir que el principio de Carathéodory expresa la segunda ley y tratarlo como equivalente a los enunciados de Clausius o de Kelvin-Planck, no es así. Para obtener todo el contenido de la segunda ley, el principio de Carathéodory debe complementarse con el principio de Planck, según el cual el trabajo isocórico siempre aumenta la energía interna de un sistema cerrado que inicialmente estaba en su propio equilibrio termodinámico interno. ^{[18] [51] [52] [53] [ aclaración necesaria ]}

En 1926, Max Planck escribió un importante artículo sobre los fundamentos de la termodinámica. ^{[52] [54]} Indicó el principio

La energía interna de un sistema cerrado aumenta mediante un proceso adiabático, durante cuya duración el volumen del sistema permanece constante. ^{[18] [51]}

Esta formulación no menciona el calor ni la temperatura, ni siquiera la entropía, y no se basa necesariamente en esos conceptos de manera implícita, pero implica el contenido de la segunda ley. Una afirmación estrechamente relacionada es que “la presión de fricción nunca realiza trabajo positivo”. ^[55] Planck escribió: “La producción de calor por fricción es irreversible”. ^{[56] [57]}

Sin mencionar la entropía, este principio de Planck se enuncia en términos físicos. Está muy relacionado con el enunciado de Kelvin dado justo antes. ^[58] Es relevante que para un sistema con volumen y número de moles constantes , la entropía es una función monótona de la energía interna. Sin embargo, este principio de Planck no es en realidad el enunciado preferido de Planck de la segunda ley, que se cita anteriormente, en una subsección anterior de la presente sección de este artículo, y se basa en el concepto de entropía.

Claus Borgnakke y Richard E. Sonntag hacen una afirmación que, en cierto sentido, complementa el principio de Planck. No la presentan como una afirmación completa de la segunda ley:

... sólo hay una manera en la que se puede disminuir la entropía de un sistema [cerrado], y es transfiriendo calor desde el sistema. ^[59]

A diferencia del principio de Planck que acabamos de mencionar, este se basa explícitamente en el cambio de entropía. La eliminación de materia de un sistema también puede reducir su entropía.

Se ha demostrado que la segunda ley es equivalente a la energía interna U definida como una función convexa de las otras propiedades extensivas del sistema. ^[60] Es decir, cuando un sistema se describe indicando su energía interna U , una variable extensiva, como una función de su entropía S , volumen V y número molar N , es decir U = U ( S , V , N ), entonces la temperatura es igual a la derivada parcial de la energía interna con respecto a la entropía ^[61] (esencialmente equivalente a la primera ecuación TdS para V y N mantenidas constantes):

${\displaystyle T=\left({\frac {\partial U}{\partial S}}\right)_{V,N}}$

La desigualdad de Clausius, así como algunas otras afirmaciones de la segunda ley, deben ser reformuladas para tener una aplicabilidad general para todas las formas de transferencia de calor, es decir, escenarios que involucran flujos radiativos. Por ejemplo, el integrando (đQ/T) de la expresión de Clausius se aplica a la conducción y convección de calor, y al caso de transferencia de radiación de cuerpo negro (BR) infinitesimal ideal, pero no se aplica a la mayoría de los escenarios de transferencia radiativa y en algunos casos no tiene ningún significado físico. En consecuencia, la desigualdad de Clausius fue reformulada ^[62] para que sea aplicable a ciclos con procesos que involucran cualquier forma de transferencia de calor. La transferencia de entropía con flujos radiativos ( ) se toma por separado de la debida a la transferencia de calor por conducción y convección ( ), donde la temperatura se evalúa en el límite del sistema donde ocurre la transferencia de calor. La desigualdad de Clausius modificada, para todos los escenarios de transferencia de calor, puede entonces expresarse como,$\delta S_{\text{NetRad}}$$\delta Q_{CC}$$${\displaystyle \int _{\text{cycle}}({\frac {\delta Q_{CC}}{T_{b}}}+\delta S_{\text{NetRad}})<=0}$$

En pocas palabras, la desigualdad de Clausius dice que cuando se completa un ciclo, el cambio en la propiedad de estado S será cero, por lo que la entropía que se produjo durante el ciclo debe haberse transferido fuera del sistema por transferencia de calor. El (o đ) indica una integración dependiente de la trayectoria.$\delta$

Debido a la emisión inherente de radiación de toda la materia, la mayoría de los cálculos de flujo de entropía involucran flujos radiativos incidentes, reflejados y emitidos. La energía y la entropía de la radiación térmica de cuerpo negro no polarizado se calculan utilizando las expresiones de energía espectral y radiancia de entropía derivadas por Max Planck ^[63] utilizando la mecánica estadística de equilibrio, donde c es la velocidad de la luz, k es la constante de Boltzmann, h es la constante de Planck, ν es la frecuencia y las cantidades K _v y L _v son los flujos de energía y entropía por unidad de frecuencia, área y ángulo sólido. Al derivar esta radiancia de entropía espectral de cuerpo negro, con el objetivo de derivar la fórmula de energía de cuerpo negro, Planck postuló que la energía de un fotón estaba cuantizada (en parte para simplificar las matemáticas), iniciando así la teoría cuántica.$${\displaystyle K_{\nu }={\frac {2h}{c^{2}}}{\frac {\nu ^{3}}{\exp \left({\frac {h\nu }{kT}}\right)-1}},}$$$${\displaystyle L_{\nu }={\frac {2k\nu ^{2}}{c^{2}}}((1+{\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})\ln(1+{\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})-({\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})\ln({\frac {c^{2}K_{\nu }}{2h\nu ^{3}}}))}$$

También se ha utilizado un enfoque de mecánica estadística de no equilibrio para obtener el mismo resultado que Planck, lo que indica que tiene una significancia más amplia y representa una entropía de no equilibrio. ^[64] Un gráfico de K _v versus frecuencia (v) para varios valores de temperatura ( T) ​​da una familia de espectros de energía de radiación de cuerpo negro, y lo mismo para los espectros de entropía. Para los flujos de emisión de radiación de cuerpo no negro (NBR), la radiancia de entropía espectral L _v se encuentra sustituyendo los datos de radiancia de energía espectral K _v en la expresión L _v (observando que los flujos de entropía emitidos y reflejados, en general, no son independientes). Para la emisión de NBR, incluida la radiación de cuerpo gris (GR), el flujo de entropía emitido resultante, o radiancia L , tiene una mayor relación de entropía a energía ( L/K ), que la de BR. Es decir, el flujo de entropía de la emisión de NBR está más alejado del resultado de conducción y convección q / T que el de la emisión de BR. ^[65] Esta observación es consistente con las fórmulas de energía y entropía de radiación de cuerpo negro de Max Planck y es consistente con el hecho de que la emisión de radiación de cuerpo negro representa la máxima emisión de entropía para todos los materiales con la misma temperatura, así como la máxima emisión de entropía para toda la radiación con la misma radiancia energética.

El análisis de la segunda ley es valioso en el análisis científico y de ingeniería, ya que proporciona una serie de beneficios sobre el análisis de energía solo, incluyendo la base para determinar la calidad de la energía (contenido de exergía ^{[66] [67] [68]} ), comprender los fenómenos físicos fundamentales y mejorar la evaluación y optimización del rendimiento. Como resultado, una declaración conceptual del principio es muy útil en el análisis de ingeniería. Los sistemas termodinámicos se pueden clasificar por las cuatro combinaciones de entropía (S) hacia arriba o hacia abajo, y uniformidad (Y) - entre el sistema y su entorno - hacia arriba o hacia abajo. Esta categoría "especial" de procesos, la categoría IV, se caracteriza por el movimiento en la dirección de bajo desorden y baja uniformidad, contrarrestando la tendencia de la segunda ley hacia la uniformidad y el desorden. ^[69]

La segunda ley puede enunciarse conceptualmente ^[69] de la siguiente manera: la materia y la energía tienen la tendencia a alcanzar un estado de uniformidad o equilibrio interno y externo, un estado de máximo desorden (entropía). Los procesos reales de no equilibrio siempre producen entropía, lo que provoca un mayor desorden en el universo, mientras que los procesos reversibles idealizados no producen entropía y no se conoce ningún proceso que destruya la entropía. La tendencia de un sistema a acercarse a la uniformidad puede contrarrestarse, y el sistema puede volverse más ordenado o complejo, mediante la combinación de dos cosas, una fuente de trabajo o exergía y alguna forma de instrucción o inteligencia. Donde 'exergía' es el potencial de trabajo térmico, mecánico, eléctrico o químico de una fuente o flujo de energía, e 'instrucción o inteligencia', aunque subjetiva, está en el contexto del conjunto de procesos de la categoría IV.

Consideremos un ejemplo de categoría IV de fabricación y montaje robótico de vehículos en una fábrica. La maquinaria robótica requiere instrucciones y entrada de trabajo eléctrico, pero cuando se completa, los productos fabricados tienen menos uniformidad con su entorno o más complejidad (orden superior) en relación con las materias primas de las que se fabricaron. Por lo tanto, la entropía o el desorden del sistema disminuyen mientras que la tendencia a la uniformidad entre el sistema y su entorno se contrarresta. En este ejemplo, las instrucciones, así como la fuente de trabajo, pueden ser internas o externas al sistema, y ​​pueden o no cruzar el límite del sistema. Para ilustrarlo, las instrucciones pueden estar precodificadas y el trabajo eléctrico puede almacenarse en un sistema de almacenamiento de energía en el sitio. Alternativamente, el control de la maquinaria puede ser por operación remota a través de una red de comunicaciones, mientras que el trabajo eléctrico se suministra a la fábrica desde la red eléctrica local. Además, los humanos pueden desempeñar directamente, en todo o en parte, el papel que desempeña la maquinaria robótica en la fabricación. En este caso, pueden intervenir instrucciones, pero la inteligencia es responsable directa o indirectamente de la dirección o aplicación del trabajo de tal manera que se contrarreste la tendencia al desorden y la uniformidad.

También hay situaciones en las que la entropía disminuye espontáneamente por medio de transferencia de energía y entropía. Cuando no existen restricciones termodinámicas, la energía o la masa, así como la entropía que las acompaña, pueden transferirse espontáneamente fuera de un sistema en un proceso para alcanzar el equilibrio externo o la uniformidad en las propiedades intensivas del sistema con su entorno. Esto ocurre espontáneamente porque la energía o la masa transferida del sistema a su entorno da como resultado una mayor entropía en el entorno, es decir, da como resultado una mayor entropía general del sistema más su entorno. Nótese que esta transferencia de entropía requiere un desequilibrio en las propiedades, como una diferencia de temperatura. Un ejemplo de esto es la cristalización por enfriamiento del agua que puede ocurrir cuando los alrededores del sistema están por debajo de las temperaturas de congelación. La transferencia de calor sin restricciones puede ocurrir espontáneamente, lo que lleva a que las moléculas de agua se congelen en una estructura cristalizada de desorden reducido (pegándose entre sí en un cierto orden debido a la atracción molecular). La entropía del sistema disminuye, pero el sistema se acerca a la uniformidad con su entorno (categoría III).

Por otra parte, consideremos la refrigeración del agua en un ambiente cálido. Debido a la refrigeración, a medida que se extrae calor del agua, la temperatura y la entropía del agua disminuyen, a medida que el sistema se aleja de la uniformidad con su entorno o ambiente cálido (categoría IV). El punto principal, la moraleja, es que la refrigeración no solo requiere una fuente de trabajo, sino que requiere un equipo diseñado, así como inteligencia operativa precodificada o directa o instrucciones para lograr el efecto de refrigeración deseado.

Antes de que se estableciera la segunda ley, muchas personas interesadas en inventar una máquina de movimiento perpetuo habían intentado sortear las restricciones de la primera ley de la termodinámica extrayendo la enorme energía interna del entorno como potencia de la máquina. A este tipo de máquinas se las denomina "máquinas de movimiento perpetuo de segundo tipo". La segunda ley declaraba la imposibilidad de tales máquinas.

El teorema de Carnot (1824) es un principio que limita la eficiencia máxima de cualquier motor posible. La eficiencia depende únicamente de la diferencia de temperatura entre los depósitos térmicos frío y caliente. El teorema de Carnot establece:

• Todos los motores térmicos irreversibles entre dos depósitos de calor son menos eficientes que un motor de Carnot que funciona entre los mismos depósitos.
• Todos los motores térmicos reversibles entre dos depósitos de calor son igualmente eficientes y un motor de Carnot funciona entre los mismos depósitos.

En su modelo ideal, el calor del calórico convertido en trabajo podría recuperarse invirtiendo el movimiento del ciclo, un concepto conocido posteriormente como reversibilidad termodinámica . Sin embargo, Carnot postuló además que se pierde algo de calor, que no se convierte en trabajo mecánico. Por lo tanto, ninguna máquina térmica real podría lograr la reversibilidad del ciclo de Carnot y estaba condenada a ser menos eficiente.

Aunque se formuló en términos de calórico (véase la obsoleta teoría calórica ), en lugar de entropía , esta fue una idea temprana de la segunda ley.

El teorema de Clausius (1854) establece que en un proceso cíclico

${\displaystyle \oint {\frac {\delta Q}{T_{\text{surr}}}}\leq 0.}$

La igualdad se cumple en el caso reversible ^[70] y la desigualdad estricta se cumple en el caso irreversible, con T _surr como la temperatura del baño de calor (alrededor) aquí. El caso reversible se utiliza para introducir la función de estado entropía . Esto se debe a que en los procesos cíclicos la variación de una función de estado es cero a partir de la funcionalidad del estado.

Para un motor térmico arbitrario, la eficiencia es:

${\displaystyle \eta ={\frac {|W_{n}|}{q_{\text{H}}}}={\frac {q_{H}+q_{\text{C}}}{q_{\text{H}}}}=1-{\frac {|q_{\text{C}}|}{|q_{\text{H}}|}}}$

( 1 )

donde W _n es el trabajo neto realizado por el motor por ciclo, q _H > 0 es el calor añadido al motor desde un depósito caliente, y q _C = −| q _C | < 0 ^[71] es el calor residual que el motor emite hacia un depósito frío. Por lo tanto, la eficiencia depende únicamente de la relación | q _C | / | q _H |.

El teorema de Carnot establece que todas las máquinas térmicas reversibles que funcionan entre los mismos depósitos de calor tienen la misma eficiencia. Por lo tanto, cualquier máquina térmica reversible que funcione entre las temperaturas T _H y T _C debe tener la misma eficiencia, es decir, la eficiencia es función únicamente de las temperaturas:

${\displaystyle {\frac {|q_{\text{C}}|}{|q_{\text{H}}|}}=f(T_{\text{H}},T_{\text{C}}).}$

( 2 )

Además, un motor térmico reversible que funciona entre las temperaturas T ₁ y T ₃ debe tener la misma eficiencia que uno que consta de dos ciclos, uno entre T ₁ y otra temperatura (intermedia) T ₂ , y el segundo entre T ₂ y T ₃ , donde T ₁ > T ₂ > T ₃ . Esto se debe a que, si una parte del motor de dos ciclos está oculta de manera que se reconoce como un motor entre los depósitos a las temperaturas T ₁ y T ₃ , entonces la eficiencia de este motor debe ser la misma que la del otro motor en los mismos depósitos. Si elegimos motores de manera que el trabajo realizado por el motor de un ciclo y el motor de dos ciclos sea el mismo, entonces la eficiencia de cada motor térmico se escribe como se muestra a continuación.

${\displaystyle \eta _{1}=1-{\frac {|q_{3}|}{|q_{1}|}}=1-f(T_{1},T_{3})}$,

${\displaystyle \eta _{2}=1-{\frac {|q_{2}|}{|q_{1}|}}=1-f(T_{1},T_{2})}$,

${\displaystyle \eta _{3}=1-{\frac {|q_{3}|}{|q_{2}|}}=1-f(T_{2},T_{3})}$.

Aquí, el motor 1 es el motor de un ciclo, y los motores 2 y 3 forman el motor de dos ciclos donde existe el depósito intermedio en T ₂ . También hemos utilizado el hecho de que el calor pasa a través del depósito térmico intermedio en sin perder su energía. (Es decir, no se pierde durante su paso a través del depósito en ). Este hecho puede demostrarse mediante lo siguiente.${\displaystyle q_{2}}$${\displaystyle T_{2}}$${\displaystyle q_{2}}$${\displaystyle T_{2}}$

${\displaystyle {\begin{aligned}&{{\eta }_{2}}=1-{\frac {|{{q}_{2}}|}{|{{q}_{1}}|}}\to |{{w}_{2}}|=|{{q}_{1}}|-|{{q}_{2}}|,\\&{{\eta }_{3}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{2}}^{*}|}}\to |{{w}_{3}}|=|{{q}_{2}}^{*}|-|{{q}_{3}}|,\\&|{{w}_{2}}|+|{{w}_{3}}|=(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|),\\&{{\eta }_{1}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{1}}|}}={\frac {(|{{w}_{2}}|+|{{w}_{3}}|)}{|{{q}_{1}}|}}={\frac {(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|)}{|{{q}_{1}}|}}.\\\end{aligned}}}$

Para tener consistencia en la última ecuación, el calor que fluye desde el motor 2 al depósito intermedio debe ser igual al calor que fluye desde el depósito hacia el motor 3.${\displaystyle q_{2}}$${\displaystyle q_{2}^{*}}$

Entonces

${\displaystyle f(T_{1},T_{3})={\frac {|q_{3}|}{|q_{1}|}}={\frac {|q_{2}||q_{3}|}{|q_{1}||q_{2}|}}=f(T_{1},T_{2})f(T_{2},T_{3}).}$

Consideremos ahora el caso donde es una temperatura de referencia fija: la temperatura del punto triple del agua es 273,16 K; . Entonces, para cualquier T ₂ y T ₃ ,${\displaystyle T_{1}}$${\displaystyle T_{1}=\mathrm {273.16~K} }$

${\displaystyle f(T_{2},T_{3})={\frac {f(T_{1},T_{3})}{f(T_{1},T_{2})}}={\frac {273.16{\text{ K}}\cdot f(T_{1},T_{3})}{273.16{\text{ K}}\cdot f(T_{1},T_{2})}}.}$

Por lo tanto, si la temperatura termodinámica T * se define por

${\displaystyle T^{*}=273.16{\text{ K}}\cdot f(T_{1},T)}$

Entonces la función f , vista como una función de las temperaturas termodinámicas, es simplemente

${\displaystyle f(T_{2},T_{3})=f(T_{2}^{*},T_{3}^{*})={\frac {T_{3}^{*}}{T_{2}^{*}}},}$

y la temperatura de referencia T ₁ * = 273,16 K × f ( T ₁ , T ₁ ) = 273,16 K. (Se puede utilizar cualquier temperatura de referencia y cualquier valor numérico positivo; la elección aquí corresponde a la escala Kelvin ).

Según la igualdad de Clausius , para un proceso reversible

${\displaystyle \oint {\frac {\delta Q}{T}}=0}$

Esto significa que la integral de línea es independiente de la trayectoria para los procesos reversibles.${\displaystyle \int _{L}{\frac {\delta Q}{T}}}$

Así podemos definir una función de estado S llamada entropía, que para un proceso reversible o para transferencia de calor pura satisface

${\displaystyle dS={\frac {\delta Q}{T}}}$

Con esto sólo podemos obtener la diferencia de entropía integrando la fórmula anterior. Para obtener el valor absoluto, necesitamos la tercera ley de la termodinámica , que establece que S = 0 en el cero absoluto para cristales perfectos.

Para cualquier proceso irreversible, dado que la entropía es una función de estado, siempre podemos conectar los estados inicial y terminal con un proceso reversible imaginario e integrar en ese camino para calcular la diferencia de entropía.

Ahora invierta el proceso reversible y combínelo con el mencionado proceso irreversible. Aplicando la desigualdad de Clausius a este bucle, con T _surr como la temperatura del entorno,

${\displaystyle -\Delta S+\int {\frac {\delta Q}{T_{\text{surr}}}}=\oint {\frac {\delta Q}{T_{\text{surr}}}}\leq 0}$

De este modo,

${\displaystyle \Delta S\geq \int {\frac {\delta Q}{T_{\text{surr}}}}}$

donde la igualdad se cumple si la transformación es reversible. Si el proceso es un proceso adiabático , entonces , por lo que .${\displaystyle \delta Q=0}$${\displaystyle \Delta S\geq 0}$

Un caso especial idealizado importante y revelador es considerar la aplicación de la segunda ley al escenario de un sistema aislado (llamado el sistema total o universo), compuesto de dos partes: un subsistema de interés y el entorno del subsistema. Se imagina que estos entornos son tan grandes que pueden considerarse como un depósito de calor ilimitado a temperatura T _R y presión P _R  – de modo que no importa cuánto calor se transfiera hacia (o desde) el subsistema, la temperatura de los alrededores seguirá siendo T _R ; y no importa cuánto se expanda (o contraiga) el volumen del subsistema, la presión de los alrededores seguirá siendo P _R .

Cualesquiera que sean los cambios en dS y dS _R que ocurran en las entropías del subsistema y de los alrededores individualmente, la entropía S _tot del sistema total aislado no debe disminuir de acuerdo con la segunda ley de la termodinámica:

${\displaystyle dS_{\mathrm {tot} }=dS+dS_{\text{R}}\geq 0}$

De acuerdo con la primera ley de la termodinámica , el cambio dU en la energía interna del subsistema es la suma del calor δq añadido al subsistema, menos cualquier trabajo δw realizado por el subsistema, más cualquier energía química neta que ingresa al subsistema d Σ μ _iR N _i , de modo que:

${\displaystyle dU=\delta q-\delta w+d\left(\sum \mu _{iR}N_{i}\right)}$

donde μ _iR son los potenciales químicos de las especies químicas en el entorno externo.

Ahora el calor que sale del depósito y entra al subsistema es

${\displaystyle \delta q=T_{\text{R}}(-dS_{\text{R}})\leq T_{\text{R}}dS}$

donde hemos utilizado primero la definición de entropía en termodinámica clásica (alternativamente, en termodinámica estadística, se puede derivar la relación entre el cambio de entropía, la temperatura y el calor absorbido); y luego la desigualdad de la segunda ley de arriba.

Por lo tanto, se deduce que cualquier trabajo neto δw realizado por el subsistema debe obedecer

${\displaystyle \delta w\leq -dU+T_{\text{R}}dS+\sum \mu _{iR}dN_{i}}$

Es útil separar el trabajo δw realizado por el subsistema en el trabajo útil δw _u que puede realizar el subsistema, además del trabajo p _R dV realizado simplemente por el subsistema expandiéndose contra la presión externa circundante, obteniéndose la siguiente relación para el trabajo útil (exergía) que puede realizar:

${\displaystyle \delta w_{u}\leq -d\left(U-T_{\text{R}}S+p_{\text{R}}V-\sum \mu _{iR}N_{i}\right)}$

Es conveniente definir el lado derecho como la derivada exacta de un potencial termodinámico, llamado disponibilidad o exergía E del subsistema,

${\displaystyle E=U-T_{\text{R}}S+p_{\text{R}}V-\sum \mu _{iR}N_{i}}$

La segunda ley implica, por tanto, que para cualquier proceso que pueda considerarse dividido simplemente en un subsistema y un depósito de temperatura y presión ilimitados con el que está en contacto,

${\displaystyle dE+\delta w_{u}\leq 0}$

es decir, el cambio en la exergía del subsistema más el trabajo útil realizado por el subsistema (o el cambio en la exergía del subsistema menos cualquier trabajo, adicional al realizado por el depósito de presión, realizado sobre el sistema) debe ser menor o igual a cero.

En resumen, si se elige un estado de referencia adecuado tipo reservorio infinito como entorno del sistema en el mundo real, entonces la segunda ley predice una disminución en E para un proceso irreversible y ningún cambio para un proceso reversible.

${\displaystyle dS_{\text{tot}}\geq 0}$es equivalente a${\displaystyle dE+\delta w_{u}\leq 0}$

Esta expresión, junto con el estado de referencia asociado, permite a un ingeniero de diseño que trabaje a escala macroscópica (por encima del límite termodinámico ) utilizar la segunda ley sin medir o considerar directamente el cambio de entropía en un sistema totalmente aislado (véase también Ingeniero de procesos ). Esos cambios ya se han considerado suponiendo que el sistema en cuestión puede alcanzar el equilibrio con el estado de referencia sin alterarlo. También se puede encontrar una eficiencia para un proceso o un conjunto de procesos que lo compare con el ideal reversible (véase Eficiencia exergética ).

Este enfoque de la segunda ley se utiliza ampliamente en la práctica de la ingeniería , la contabilidad ambiental , la ecología de sistemas y otras disciplinas.

La segunda ley determina si un proceso físico o químico propuesto está prohibido o puede ocurrir espontáneamente. En el caso de los sistemas aislados , el entorno no proporciona energía y la segunda ley exige que la entropía del sistema por sí sola aumente: Δ S > 0. Algunos ejemplos de procesos físicos espontáneos en sistemas aislados son los siguientes:

• 1) El calor se puede transferir desde una región de mayor temperatura a una de menor temperatura (pero no al revés).
• 2) La energía mecánica se puede convertir en energía térmica (pero no al revés).
• 3) Un soluto puede moverse de una región de mayor concentración a una región de menor concentración (pero no al revés).

Sin embargo, en el caso de algunos sistemas no aislados que pueden intercambiar energía con su entorno, el entorno intercambia suficiente calor con el sistema o realiza suficiente trabajo sobre el sistema, de modo que los procesos se producen en dirección opuesta. Esto es posible siempre que el cambio de entropía total del sistema más el entorno sea positivo, como lo exige la segunda ley: Δ S _tot = Δ S + Δ S _R > 0. Para los tres ejemplos dados anteriormente:

• 1) El calor puede transferirse desde una región de temperatura más baja a una de temperatura más alta en un refrigerador o en una bomba de calor . Estas máquinas deben proporcionar suficiente trabajo al sistema.
• 2) La energía térmica se puede convertir en trabajo mecánico en un motor térmico , si también se expulsa suficiente calor al entorno.
• 3) Un soluto puede moverse desde una región de menor concentración a una región de mayor concentración en el proceso bioquímico de transporte activo , si se proporciona suficiente trabajo mediante un gradiente de concentración de una sustancia química como el ATP o mediante un gradiente electroquímico .

Para un proceso químico espontáneo en un sistema cerrado a temperatura y presión constantes sin trabajo no PV , la desigualdad de Clausius Δ S > Q/T _surr se transforma en una condición para el cambio en la energía libre de Gibbs.

${\displaystyle \Delta G<0}$

o d G < 0. Para un proceso similar a temperatura y volumen constantes, el cambio en la energía libre de Helmholtz debe ser negativo, . Por lo tanto, un valor negativo del cambio en la energía libre ( G o A ) es una condición necesaria para que un proceso sea espontáneo. Esta es la forma más útil de la segunda ley de la termodinámica en química, donde los cambios de energía libre se pueden calcular a partir de entalpías de formación tabuladas y entropías molares estándar de reactivos y productos. ^{[19] [15]} La condición de equilibrio químico a T y p constantes sin trabajo eléctrico es d G = 0.${\displaystyle \Delta A<0}$

La primera teoría de la conversión de calor en trabajo mecánico se debe a Nicolas Léonard Sadi Carnot en 1824. Fue el primero en comprender correctamente que la eficiencia de esta conversión depende de la diferencia de temperatura entre un motor y su entorno.

Reconociendo la importancia del trabajo de James Prescott Joule sobre la conservación de la energía, Rudolf Clausius fue el primero en formular la segunda ley en 1850, en esta forma: el calor no fluye espontáneamente de los cuerpos fríos a los calientes. Aunque ahora es de conocimiento común, esto era contrario a la teoría calórica del calor popular en ese momento, que consideraba el calor como un fluido. De allí pudo inferir el principio de Sadi Carnot y la definición de entropía (1865).

Establecida durante el siglo XIX, la segunda ley de Kelvin-Planck dice: "Es imposible que cualquier dispositivo que funcione en un ciclo reciba calor de un solo depósito y produzca una cantidad neta de trabajo". Se demostró que esta afirmación era equivalente a la de Clausius.

La hipótesis ergódica también es importante para el enfoque de Boltzmann . Esta hipótesis dice que, durante largos períodos de tiempo, el tiempo transcurrido en alguna región del espacio de fases de microestados con la misma energía es proporcional al volumen de esta región, es decir, que todos los microestados accesibles son igualmente probables durante un largo período de tiempo. De manera equivalente, dice que el promedio de tiempo y el promedio sobre el conjunto estadístico son los mismos.

Existe una doctrina tradicional, que comenzó con Clausius, según la cual la entropía puede entenderse en términos de «desorden» molecular dentro de un sistema macroscópico . Esta doctrina está obsoleta. ^{[72] [73] [74]}

En 1865, el físico alemán Rudolf Clausius enunció lo que llamó el "segundo teorema fundamental en la teoría mecánica del calor " en la siguiente forma: ^[75]

${\displaystyle \int {\frac {\delta Q}{T}}=-N}$

donde Q es el calor, T la temperatura y N el "valor de equivalencia" de todas las transformaciones no compensadas que intervienen en un proceso cíclico. Más tarde, en 1865, Clausius definiría el "valor de equivalencia" como entropía. Inmediatamente después de esta definición, ese mismo año, la versión más famosa de la segunda ley se leyó en una presentación en la Sociedad Filosófica de Zúrich el 24 de abril, en la que, al final de su presentación, Clausius concluye:

La entropía del universo tiende a un máximo.

Esta afirmación es la forma más conocida de expresar la segunda ley. Debido a la vaguedad de su lenguaje (por ejemplo, universo ) y a la falta de condiciones específicas (por ejemplo, abierto, cerrado o aislado), muchas personas interpretan esta sencilla afirmación como que la segunda ley de la termodinámica se aplica prácticamente a todos los temas imaginables. Esto no es cierto; esta afirmación es sólo una versión simplificada de una descripción más amplia y precisa.

En términos de variación temporal, el enunciado matemático de la segunda ley para un sistema aislado que sufre una transformación arbitraria es:

${\displaystyle {\frac {dS}{dt}}\geq 0}$

dónde

S es la entropía del sistema y

Es hora .​

El signo de igualdad se aplica después del equilibrio. Una forma alternativa de formular la segunda ley para sistemas aislados es:

${\displaystyle {\frac {dS}{dt}}={\dot {S}}_{\text{i}}}$con${\displaystyle {\dot {S}}_{\text{i}}\geq 0}$

con la suma de la tasa de producción de entropía por todos los procesos dentro del sistema. La ventaja de esta formulación es que muestra el efecto de la producción de entropía. La tasa de producción de entropía es un concepto muy importante ya que determina (limita) la eficiencia de las máquinas térmicas. Multiplicada por la temperatura ambiente da la llamada energía disipada .${\displaystyle {\dot {S}}_{\text{i}}}$${\displaystyle T_{\text{a}}}$${\displaystyle P_{\text{diss}}=T_{\text{a}}{\dot {S}}_{\text{i}}}$

La expresión de la segunda ley para sistemas cerrados (es decir, que permiten el intercambio de calor y el movimiento de los límites, pero no el intercambio de materia) es:

${\displaystyle {\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}_{\text{i}}}$con${\displaystyle {\dot {S}}_{\text{i}}\geq 0}$

Aquí,

${\displaystyle {\dot {Q}}}$es el flujo de calor en el sistema

${\displaystyle T}$es la temperatura en el punto donde el calor entra al sistema.

El signo de igualdad se cumple en el caso de que sólo se produzcan procesos reversibles en el interior del sistema. Si se producen procesos irreversibles (como ocurre en los sistemas reales en funcionamiento), se cumple el signo >. Si se suministra calor al sistema en varios puntos, tenemos que realizar la suma algebraica de los términos correspondientes.

Para sistemas abiertos (que también permiten el intercambio de materia):

${\displaystyle {\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}+{\dot {S}}_{\text{i}}}$con${\displaystyle {\dot {S}}_{\text{i}}\geq 0}$

Aquí, el flujo de entropía hacia el sistema está asociado con el flujo de materia que ingresa al sistema. No debe confundirse con la derivada temporal de la entropía. Si se aporta materia en varios lugares, debemos tomar la suma algebraica de estas contribuciones.${\displaystyle {\dot {S}}}$

La mecánica estadística explica la segunda ley al postular que un material está compuesto de átomos y moléculas que están en constante movimiento. Un conjunto particular de posiciones y velocidades para cada partícula en el sistema se denomina microestado del sistema y, debido al movimiento constante, el sistema cambia constantemente su microestado. La mecánica estadística postula que, en equilibrio, cada microestado en el que pueda estar el sistema tiene la misma probabilidad de ocurrir, y cuando se hace esta suposición, conduce directamente a la conclusión de que la segunda ley debe cumplirse en un sentido estadístico. Es decir, la segunda ley se cumplirá en promedio, con una variación estadística del orden de 1/ √ N donde N es el número de partículas en el sistema. Para situaciones cotidianas (macroscópicas), la probabilidad de que se viole la segunda ley es prácticamente cero. Sin embargo, para sistemas con un pequeño número de partículas, los parámetros termodinámicos, incluida la entropía, pueden mostrar desviaciones estadísticas significativas de lo predicho por la segunda ley. La teoría termodinámica clásica no se ocupa de estas variaciones estadísticas.

El primer argumento mecánico de la teoría cinética de los gases de que las colisiones moleculares implican una igualación de temperaturas y, por lo tanto, una tendencia hacia el equilibrio se debió a James Clerk Maxwell en 1860; ^[76] Ludwig Boltzmann con su teorema H de 1872 también argumentó que debido a las colisiones los gases deberían con el tiempo tender hacia la distribución de Maxwell-Boltzmann .

Debido a la paradoja de Loschmidt , las derivaciones de la segunda ley tienen que hacer una suposición con respecto al pasado, a saber, que el sistema no está correlacionado en algún momento en el pasado; esto permite un tratamiento probabilístico simple. Esta suposición suele considerarse como una condición de contorno y, por lo tanto, la segunda ley es en última instancia una consecuencia de las condiciones iniciales en algún lugar en el pasado, probablemente al comienzo del universo (el Big Bang ), aunque también se han sugerido otros escenarios . ^{[77] [78] [79]}

Dadas estas suposiciones, en mecánica estadística, la segunda ley no es un postulado, sino una consecuencia del postulado fundamental , también conocido como postulado de probabilidad previa igual, siempre que uno tenga claro que los argumentos de probabilidad simple se aplican solo al futuro, mientras que para el pasado hay fuentes auxiliares de información que nos dicen que era de baja entropía. ^{[ cita requerida ]} La primera parte de la segunda ley, que establece que la entropía de un sistema aislado térmicamente solo puede aumentar, es una consecuencia trivial del postulado de probabilidad previa igual, si restringimos la noción de entropía a sistemas en equilibrio térmico. La entropía de un sistema aislado en equilibrio térmico que contiene una cantidad de energía de es:${\displaystyle E}$

${\displaystyle S=k_{\mathrm {B} }\ln \left[\Omega \left(E\right)\right]}$

donde es el número de estados cuánticos en un pequeño intervalo entre y . Aquí hay un intervalo de energía macroscópicamente pequeño que se mantiene fijo. Estrictamente hablando, esto significa que la entropía depende de la elección de . Sin embargo, en el límite termodinámico (es decir, en el límite de un tamaño de sistema infinitamente grande), la entropía específica (entropía por unidad de volumen o por unidad de masa) no depende de .${\displaystyle \Omega \left(E\right)}$${\displaystyle E}$${\displaystyle E+\delta E}$${\displaystyle \delta E}$${\displaystyle \delta E}$${\displaystyle \delta E}$

Supongamos que tenemos un sistema aislado cuyo estado macroscópico está especificado por una serie de variables. Estas variables macroscópicas pueden referirse, por ejemplo, al volumen total, a las posiciones de los pistones en el sistema, etc. Entonces dependerá de los valores de estas variables. Si una variable no es fija (por ejemplo, no fijamos un pistón en una posición determinada), entonces, como todos los estados accesibles son igualmente probables en equilibrio, la variable libre en equilibrio será tal que se maximice en la energía dada del sistema aislado ^[80], ya que esa es la situación más probable en equilibrio.${\displaystyle \Omega }$${\displaystyle \Omega }$

Si la variable se fijó inicialmente en algún valor, luego, al liberarla y cuando se haya alcanzado el nuevo equilibrio, el hecho de que la variable se ajuste por sí sola de modo que se maximice, implica que la entropía habrá aumentado o se habrá mantenido igual (si el valor en el que se fijó la variable resultó ser el valor de equilibrio). Supongamos que partimos de una situación de equilibrio y de repente eliminamos una restricción sobre una variable. Entonces, justo después de hacer esto, hay una serie de microestados accesibles, pero el equilibrio aún no se ha alcanzado, por lo que las probabilidades reales de que el sistema esté en algún estado accesible aún no son iguales a la probabilidad previa de . Ya hemos visto que en el estado de equilibrio final, la entropía habrá aumentado o se habrá mantenido igual en relación con el estado de equilibrio anterior. Sin embargo, el teorema H de Boltzmann demuestra que la cantidad H aumenta monótonamente como una función del tiempo durante el estado intermedio fuera del equilibrio.${\displaystyle \Omega }$${\displaystyle \Omega }$${\displaystyle 1/\Omega }$

La segunda parte de la segunda ley establece que el cambio de entropía de un sistema que experimenta un proceso reversible viene dado por:

${\displaystyle dS={\frac {\delta Q}{T}}}$

donde la temperatura se define como:

${\displaystyle {\frac {1}{k_{\mathrm {B} }T}}\equiv \beta \equiv {\frac {d\ln \left[\Omega \left(E\right)\right]}{dE}}}$

Véase el conjunto microcanónico para la justificación de esta definición. Supongamos que el sistema tiene algún parámetro externo, x , que puede cambiarse. En general, los estados propios de energía del sistema dependerán de x . Según el teorema adiabático de la mecánica cuántica, en el límite de un cambio infinitamente lento del hamiltoniano del sistema, el sistema permanecerá en el mismo estado propio de energía y, por lo tanto, cambiará su energía de acuerdo con el cambio de energía del estado propio de energía en el que se encuentra.

La fuerza generalizada, X , correspondiente a la variable externa x se define de modo que sea el trabajo realizado por el sistema si x se incrementa en una cantidad dx . Por ejemplo, si x es el volumen, entonces X es la presión. La fuerza generalizada para un sistema que se sabe que está en estado propio de energía viene dada por:${\displaystyle Xdx}$${\displaystyle E_{r}}$

${\displaystyle X=-{\frac {dE_{r}}{dx}}}$

Dado que el sistema puede estar en cualquier estado propio de energía dentro de un intervalo de , definimos la fuerza generalizada para el sistema como el valor esperado de la expresión anterior:${\displaystyle \delta E}$

${\displaystyle X=-\left\langle {\frac {dE_{r}}{dx}}\right\rangle \,}$

Para evaluar el promedio, dividimos los estados propios de energía contando cuántos de ellos tienen un valor para dentro de un rango entre y . Llamando a este número , tenemos:${\displaystyle \Omega \left(E\right)}$${\displaystyle {\frac {dE_{r}}{dx}}}$${\displaystyle Y}$${\displaystyle Y+\delta Y}$${\displaystyle \Omega _{Y}\left(E\right)}$

${\displaystyle \Omega \left(E\right)=\sum _{Y}\Omega _{Y}\left(E\right)\,}$

El promedio que define la fuerza generalizada ahora se puede escribir:

${\displaystyle X=-{\frac {1}{\Omega \left(E\right)}}\sum _{Y}Y\Omega _{Y}\left(E\right)\,}$

Podemos relacionar esto con la derivada de la entropía con respecto a x a energía constante E de la siguiente manera. Supongamos que cambiamos x a x + dx . Entonces cambiará porque los estados propios de energía dependen de x , lo que hace que los estados propios de energía se muevan dentro o fuera del rango entre y . Centrémonos de nuevo en los estados propios de energía para los que se encuentra dentro del rango entre y . Dado que estos estados propios de energía aumentan en energía en Y dx , todos los estados propios de energía que están en el intervalo que va desde E – Y dx a E se mueven desde debajo de E a encima de E . Hay${\displaystyle \Omega \left(E\right)}$${\displaystyle E}$${\displaystyle E+\delta E}$${\textstyle {\frac {dE_{r}}{dx}}}$${\displaystyle Y}$${\displaystyle Y+\delta Y}$

${\displaystyle N_{Y}\left(E\right)={\frac {\Omega _{Y}\left(E\right)}{\delta E}}Ydx\,}$

tales estados propios de energía. Si , todos estos estados propios de energía se moverán dentro del rango entre y y contribuirán a un aumento en . La cantidad de estados propios de energía que se mueven de abajo hacia arriba está dada por . La diferencia${\displaystyle Ydx\leq \delta E}$${\displaystyle E}$${\displaystyle E+\delta E}$${\displaystyle \Omega }$${\displaystyle E+\delta E}$${\displaystyle E+\delta E}$${\displaystyle N_{Y}\left(E+\delta E\right)}$

${\displaystyle N_{Y}\left(E\right)-N_{Y}\left(E+\delta E\right)\,}$

es por lo tanto la contribución neta al aumento de . Si Y dx es mayor que habrá estados propios de energía que se mueven desde debajo de E hasta arriba de . Se cuentan tanto en como , por lo tanto, la expresión anterior también es válida en ese caso.${\displaystyle \Omega }$${\displaystyle \delta E}$${\displaystyle E+\delta E}$${\displaystyle N_{Y}\left(E\right)}$${\displaystyle N_{Y}\left(E+\delta E\right)}$

Expresando la expresión anterior como derivada con respecto a E y sumando sobre Y se obtiene la expresión:

${\displaystyle \left({\frac {\partial \Omega }{\partial x}}\right)_{E}=-\sum _{Y}Y\left({\frac {\partial \Omega _{Y}}{\partial E}}\right)_{x}=\left({\frac {\partial \left(\Omega X\right)}{\partial E}}\right)_{x}\,}$

La derivada logarítmica de con respecto a x viene dada por:${\displaystyle \Omega }$

${\displaystyle \left({\frac {\partial \ln \left(\Omega \right)}{\partial x}}\right)_{E}=\beta X+\left({\frac {\partial X}{\partial E}}\right)_{x}\,}$

El primer término es intensivo, es decir, no escala con el tamaño del sistema. Por el contrario, el último término escala con el tamaño inverso del sistema y, por lo tanto, se desvanecerá en el límite termodinámico. Por lo tanto, hemos descubierto que:

${\displaystyle \left({\frac {\partial S}{\partial x}}\right)_{E}={\frac {X}{T}}\,}$

Combinando esto con

${\displaystyle \left({\frac {\partial S}{\partial E}}\right)_{x}={\frac {1}{T}}\,}$

da:

${\displaystyle dS=\left({\frac {\partial S}{\partial E}}\right)_{x}dE+\left({\frac {\partial S}{\partial x}}\right)_{E}dx={\frac {dE}{T}}+{\frac {X}{T}}dx={\frac {\delta Q}{T}}\,}$

Si un sistema está en contacto térmico con un baño de calor a una temperatura T , entonces, en equilibrio, la distribución de probabilidad sobre los valores propios de energía está dada por el conjunto canónico :

${\displaystyle P_{j}={\frac {\exp \left(-{\frac {E_{j}}{k_{\mathrm {B} }T}}\right)}{Z}}}$

Aquí Z es un factor que normaliza la suma de todas las probabilidades a 1, esta función se conoce como función de partición . Consideremos ahora un cambio infinitesimal reversible en la temperatura y en los parámetros externos de los que dependen los niveles de energía. De la fórmula general para la entropía se deduce:

${\displaystyle S=-k_{\mathrm {B} }\sum _{j}P_{j}\ln \left(P_{j}\right)}$

eso

${\displaystyle dS=-k_{\mathrm {B} }\sum _{j}\ln \left(P_{j}\right)dP_{j}}$

Insertando la fórmula para el conjunto canónico aquí obtenemos:${\displaystyle P_{j}}$

${\displaystyle dS={\frac {1}{T}}\sum _{j}E_{j}dP_{j}={\frac {1}{T}}\sum _{j}d\left(E_{j}P_{j}\right)-{\frac {1}{T}}\sum _{j}P_{j}dE_{j}={\frac {dE+\delta W}{T}}={\frac {\delta Q}{T}}}$

Como se explicó anteriormente, se cree que la segunda ley de la termodinámica es resultado de las condiciones iniciales de muy baja entropía en el Big Bang . Desde un punto de vista estadístico, estas eran condiciones muy especiales. Por otro lado, eran bastante simples, ya que el universo -o al menos la parte del mismo a partir de la cual se desarrolló el universo observable- parece haber sido extremadamente uniforme. ^[81]

Esto puede parecer algo paradójico, ya que en muchos sistemas físicos las condiciones uniformes (por ejemplo, gases mezclados en lugar de separados) tienen una entropía alta. La paradoja se resuelve una vez que se comprende que los sistemas gravitacionales tienen capacidad calorífica negativa , de modo que cuando la gravedad es importante, las condiciones uniformes (por ejemplo, un gas de densidad uniforme) de hecho tienen una entropía menor en comparación con las no uniformes (por ejemplo, agujeros negros en el espacio vacío). ^[82] Otro enfoque más es que el universo tenía una entropía alta (o incluso máxima) dado su tamaño, pero a medida que el universo creció salió rápidamente del equilibrio termodinámico, su entropía solo aumentó ligeramente en comparación con el aumento de la entropía máxima posible, y por lo tanto llegó a una entropía muy baja en comparación con el máximo posible mucho mayor dado su tamaño posterior. ^[83]

En cuanto a la razón por la cual las condiciones iniciales fueron así, una sugerencia es que la inflación cosmológica fue suficiente para eliminar la falta de suavidad, mientras que otra es que el universo fue creado espontáneamente , donde el mecanismo de creación implica condiciones iniciales de baja entropía. ^[84]

Existen dos formas principales de formular la termodinámica: (a) a través de pasos de un estado de equilibrio termodinámico a otro, y (b) a través de procesos cíclicos, mediante los cuales el sistema permanece inalterado, mientras que la entropía total del entorno aumenta. Estas dos formas ayudan a comprender los procesos de la vida. La termodinámica de los organismos vivos ha sido considerada por muchos autores, entre ellos Erwin Schrödinger (en su libro ¿Qué es la vida? ) y Léon Brillouin . ^[85]

En una aproximación justa, los organismos vivos pueden considerarse como ejemplos de (b). Aproximadamente, el estado físico de un animal cambia día a día, dejando al animal casi sin cambios. Los animales toman alimento, agua y oxígeno y, como resultado del metabolismo , emiten productos de descomposición y calor. Las plantas absorben energía radiativa del sol, que puede considerarse calor, y dióxido de carbono y agua. Emiten oxígeno. De esta manera crecen. Finalmente mueren y sus restos se pudren, convirtiéndose en su mayoría de nuevo en dióxido de carbono y agua. Esto puede considerarse un proceso cíclico. En general, la luz solar proviene de una fuente de alta temperatura, el sol, y su energía pasa a un sumidero de temperatura más baja, es decir, se irradia al espacio. Esto es un aumento de la entropía de los alrededores de la planta. Por lo tanto, los animales y las plantas obedecen la segunda ley de la termodinámica, considerada en términos de procesos cíclicos.

Además, la capacidad de los organismos vivos de crecer y aumentar su complejidad, así como de formar correlaciones con su entorno en forma de adaptación y memoria, no se opone a la segunda ley; más bien, es similar a los resultados generales que se derivan de ella: según algunas definiciones, un aumento de la entropía también resulta en un aumento de la complejidad ^[86], y para un sistema finito que interactúa con reservorios finitos, un aumento de la entropía es equivalente a un aumento de las correlaciones entre el sistema y los reservorios ^{[87] .}

Los organismos vivos pueden considerarse sistemas abiertos, porque la materia entra y sale de ellos. La termodinámica de los sistemas abiertos se considera actualmente en términos de pasajes de un estado de equilibrio termodinámico a otro, o en términos de flujos en la aproximación del equilibrio termodinámico local. El problema para los organismos vivos puede simplificarse aún más mediante la aproximación de suponer un estado estable con flujos inmutables. Los principios generales de producción de entropía para tales aproximaciones son un tema de investigación en curso .

Por lo general, los sistemas en los que la gravedad no es importante tienen una capacidad térmica positiva , es decir, su temperatura aumenta con su energía interna. Por lo tanto, cuando la energía fluye desde un objeto de alta temperatura a un objeto de baja temperatura, la temperatura de la fuente disminuye mientras que la temperatura del sumidero aumenta; por lo tanto, las diferencias de temperatura tienden a disminuir con el tiempo.

Este no siempre es el caso de los sistemas en los que la fuerza gravitacional es importante: los sistemas que están limitados por su propia gravedad, como las estrellas, pueden tener capacidades térmicas negativas. A medida que se contraen, tanto su energía total como su entropía disminuyen ^[88] pero su temperatura interna puede aumentar . Esto puede ser significativo para las protoestrellas e incluso para los planetas gigantes gaseosos como Júpiter . Sin embargo, cuando se incluye la entropía de la radiación de cuerpo negro emitida por los cuerpos, se puede demostrar que la entropía total del sistema aumenta incluso cuando la entropía del planeta o la estrella disminuye. ^[89]

La teoría de la termodinámica clásica o del equilibrio es idealizada. Un postulado o supuesto principal, a menudo ni siquiera enunciado explícitamente, es la existencia de sistemas en sus propios estados internos de equilibrio termodinámico. En general, una región del espacio que contiene un sistema físico en un momento dado, que puede encontrarse en la naturaleza, no está en equilibrio termodinámico, entendido en términos más estrictos. En términos más generales, nada en todo el universo está o ha estado nunca verdaderamente en equilibrio termodinámico exacto. ^{[90] [91]}

Para los fines del análisis físico, a menudo es bastante conveniente hacer una suposición de equilibrio termodinámico . Tal suposición puede basarse en prueba y error para su justificación. Si la suposición está justificada, a menudo puede ser muy valiosa y útil porque hace disponible la teoría de la termodinámica. Los elementos de la suposición de equilibrio son que se observa que un sistema no cambia durante un tiempo indefinidamente largo, y que hay tantas partículas en un sistema, que su naturaleza particulada puede ignorarse por completo. Bajo tal suposición de equilibrio, en general, no hay fluctuaciones macroscópicamente detectables . Hay una excepción, el caso de los estados críticos , que exhiben a simple vista el fenómeno de opalescencia crítica . Para estudios de laboratorio de estados críticos, se necesitan tiempos de observación excepcionalmente largos.

En todos los casos, la suposición de equilibrio termodinámico, una vez realizada, implica como consecuencia que ninguna posible "fluctuación" candidata altera la entropía del sistema.

Puede ocurrir fácilmente que un sistema físico presente cambios macroscópicos internos lo suficientemente rápidos como para invalidar la hipótesis de la constancia de la entropía, o que un sistema físico tenga tan pocas partículas que la naturaleza de las partículas se manifieste en fluctuaciones observables. En ese caso, debe abandonarse la hipótesis del equilibrio termodinámico. No existe una definición general absoluta de la entropía para los estados de no equilibrio. ^[92]

Hay casos intermedios, en los que el supuesto de equilibrio termodinámico local es una muy buena aproximación, ^{[93] [94] [95] [96]} pero estrictamente hablando sigue siendo una aproximación, no teóricamente ideal.

En general, para las situaciones de no equilibrio, puede ser útil considerar las definiciones mecánicas estadísticas de otras magnitudes que pueden llamarse convenientemente "entropía", pero no deben confundirse ni combinarse con la entropía termodinámica definida correctamente para la segunda ley. Estas otras magnitudes pertenecen de hecho a la mecánica estadística, no a la termodinámica, el ámbito primario de la segunda ley.

La física de las fluctuaciones observables macroscópicamente está más allá del alcance de este artículo.

La segunda ley de la termodinámica es una ley física que no es simétrica a la inversión de la dirección del tiempo. Esto no entra en conflicto con las simetrías observadas en las leyes fundamentales de la física (en particular la simetría CPT ), ya que la segunda ley se aplica estadísticamente en condiciones de contorno asimétricas en el tiempo. ^[97] La ​​segunda ley se ha relacionado con la diferencia entre avanzar y retroceder en el tiempo, o con el principio de que la causa precede al efecto ( la flecha causal del tiempo o causalidad ). ^[98]

La irreversibilidad de los procesos termodinámicos es consecuencia del carácter asimétrico de las operaciones termodinámicas y no de propiedades microscópicas irreversibles internas de los cuerpos. Las operaciones termodinámicas son intervenciones externas macroscópicas impuestas a los cuerpos participantes, no derivadas de sus propiedades internas. Existen supuestas "paradojas" que surgen de no reconocer esto.

La paradoja de Loschmidt , también conocida como paradoja de la reversibilidad, es la objeción de que no debería ser posible deducir un proceso irreversible a partir de la dinámica simétrica en el tiempo que describe la evolución microscópica de un sistema macroscópico.

En opinión de Schrödinger, "es ahora bastante obvio de qué manera hay que reformular la ley de la entropía -o, en realidad, todos los demás enunciados irreversibles- de modo que puedan derivarse de modelos reversibles. No hay que hablar de un sistema aislado, sino al menos de dos, que por el momento se pueden considerar aislados del resto del mundo, pero no siempre uno del otro". ^[99] Los dos sistemas están aislados entre sí por el muro, hasta que éste es eliminado por la operación termodinámica, tal como prevé la ley. La operación termodinámica es impuesta externamente, no está sujeta a las leyes dinámicas microscópicas reversibles que gobiernan los constituyentes de los sistemas. Es la causa de la irreversibilidad. El enunciado de la ley en este artículo cumple con el consejo de Schrödinger. La relación causa-efecto es lógicamente anterior a la segunda ley, no se deriva de ella.

El teorema de recurrencia de Poincaré considera una descripción microscópica teórica de un sistema físico aislado. Esto puede considerarse como un modelo de un sistema termodinámico después de que una operación termodinámica haya eliminado una pared interna. El sistema, después de un tiempo suficientemente largo, volverá a un estado definido microscópicamente muy cercano al inicial. El tiempo de recurrencia de Poincaré es el tiempo transcurrido hasta el retorno. Es extremadamente largo, probablemente más largo que la vida del universo, y depende sensiblemente de la geometría de la pared que fue eliminada por la operación termodinámica. El teorema de recurrencia puede percibirse como aparentemente contradictorio con la segunda ley de la termodinámica. Sin embargo, más obviamente, es simplemente un modelo microscópico de equilibrio termodinámico en un sistema aislado formado por la eliminación de una pared entre dos sistemas. Para un sistema termodinámico típico, el tiempo de recurrencia es tan grande (muchas, muchas veces más largo que la vida del universo) que, para todos los fines prácticos, uno no puede observar la recurrencia. Sin embargo, se podría desear imaginar que se podría esperar a que se produjera la recurrencia de Poincaré y luego volver a insertar la pared que se eliminó mediante la operación termodinámica. Es evidente entonces que la apariencia de irreversibilidad se debe a la absoluta imprevisibilidad de la recurrencia de Poincaré, dado únicamente que el estado inicial era uno de equilibrio termodinámico, como es el caso de la termodinámica macroscópica. Incluso si se pudiera esperar, no se tendría ninguna posibilidad práctica de elegir el instante correcto en el que volver a insertar la pared. El teorema de recurrencia de Poincaré proporciona una solución a la paradoja de Loschmidt. Si se pudiera monitorear un sistema termodinámico aislado durante un número cada vez mayor de múltiplos del tiempo promedio de recurrencia de Poincaré, el comportamiento termodinámico del sistema se volvería invariante bajo la inversión del tiempo.

James Clerk Maxwell imaginó un recipiente dividido en dos partes, A y B. Ambas partes están llenas del mismo gas a temperaturas iguales y colocadas una al lado de la otra, separadas por una pared. Observando las moléculas de ambos lados, un demonio imaginario guarda una trampilla microscópica en la pared. Cuando una molécula más rápida que el promedio de A vuela hacia la trampilla, el demonio la abre y la molécula volará de A a B. La velocidad promedio de las moléculas en B habrá aumentado mientras que en A se habrán ralentizado en promedio. Como la velocidad molecular promedio corresponde a la temperatura, la temperatura disminuye en A y aumenta en B , en contra de la segunda ley de la termodinámica. ^[100]

Una respuesta a esta pregunta fue sugerida en 1929 por Leó Szilárd y más tarde por Léon Brillouin . Szilárd señaló que un demonio de Maxwell de la vida real necesitaría tener algún medio para medir la velocidad molecular, y que el acto de adquirir información requeriría un gasto de energía. ^[101] Asimismo, Brillouin demostró que la disminución de la entropía causada por el demonio sería menor que la entropía producida al elegir moléculas en función de su velocidad. ^[100]

El «demonio» de Maxwell altera repetidamente la permeabilidad de la pared entre A y B. Por lo tanto, está realizando operaciones termodinámicas a escala microscópica, no solo observando procesos termodinámicos macroscópicos espontáneos o naturales ordinarios. ^[101]

Wikiquote tiene citas relacionadas con Segunda ley de la termodinámica .

La ley de que la entropía siempre aumenta ocupa, creo, la posición suprema entre las leyes de la naturaleza . Si alguien te señala que tu teoría favorita del universo está en desacuerdo con las ecuaciones de Maxwell , tanto peor para las ecuaciones de Maxwell. Si se descubre que la observación la contradice, bueno, estos experimentalistas a veces cometen errores. Pero si se descubre que tu teoría está en contra de la segunda ley de la termodinámica, no puedo darte ninguna esperanza; no te queda otra opción que derrumbarte en la más profunda humillación.

—  Sir Arthur Stanley Eddington , La naturaleza del mundo físico (1927)

Ha habido casi tantas formulaciones de la segunda ley como discusiones sobre ella.

—  Filósofo/físico P. W. Bridgman (1941)

Clausius es el autor de la sibílica frase: «La energía del universo es constante; la entropía del universo tiende a un máximo». Los objetivos de la termomecánica del continuo no llegan a explicar el «universo», pero dentro de esa teoría podemos derivar fácilmente una afirmación explícita que en algunos aspectos recuerda a la de Clausius, pero que se refiere sólo a un objeto modesto: un cuerpo aislado de tamaño finito.

—  Truesdell, C. , Muncaster, RG (1980). Fundamentos de la teoría cinética de Maxwell de un gas monatómico simple, tratada como una rama de la mecánica racional , Academic Press, Nueva York, ISBN  0-12-701350-4 , pág. 17.

• Goldstein, Martin e Inge F., 1993. The Refrigerator and the Universe . Harvard Univ. Press. Los capítulos 4 a 9 contienen una introducción a la segunda ley, un poco menos técnica que esta entrada. ISBN 978-0-674-75324-2 
• Leff, Harvey S. y Rex, Andrew F. (eds.) 2003. Maxwell's Demon 2: Entropía, información clásica y cuántica, computación . Bristol, Reino Unido; Filadelfia, Pensilvania: Instituto de Física . ISBN 978-0-585-49237-7 
• Halliwell, JJ (1994). Orígenes físicos de la asimetría temporal . Cambridge. ISBN 978-0-521-56837-1.(técnico).
• Carnot, Sadi (1890). Thurston, Robert Henry (ed.). Reflexiones sobre la fuerza motriz del calor y sobre las máquinas adaptadas para desarrollar esa fuerza . Nueva York: J. Wiley & Sons.(texto completo de la edición de 1897) (html Archivado el 18 de agosto de 2007 en Wayback Machine )
• Stephen Jay Kline (1999). La verdad sobre la entropía y la termodinámica interpretativa , La Cañada, CA: DCW Industries. ISBN 1-928729-01-0 . 
• Kostic, M (2011). Revisitando la segunda ley de degradación de energía y generación de entropía: del ingenioso razonamiento de Sadi Carnot a la generalización holística . Actas de la conferencia AIP. Vol. 1411. págs. 327–350. Bibcode :2011AIPC.1411..327K. CiteSeerX  10.1.1.405.1945 . doi :10.1063/1.3665247. ISBN 978-0-7354-0985-9. {{cite book}}: |journal=ignorado ( ayuda ) también en [1].

• Enciclopedia de Filosofía de Stanford : "Filosofía de la mecánica estadística", por Lawrence Sklar.
• Segunda ley de la termodinámica en el curso Termodinámica unificada y propulsión del MIT del profesor ZS Spakovszky
• ET Jaynes , 1988, "La evolución del principio de Carnot", en GJ Erickson y CR Smith (eds.) Métodos bayesianos y de máxima entropía en ciencia e ingeniería , vol. 1: pág. 267.
• Caratheodory, C., "Examen de los fundamentos de la termodinámica", trad. de DH Delphenich
• La segunda ley de la termodinámica, charla en BBC Radio 4 con John Gribbin, Peter Atkins y Monica Grady ( In Our Time , 16 de diciembre de 2004)
• Revista de la Sociedad Internacional de Historia de la Filosofía de la Ciencia, 2012