Ciclo termodinámico
| Termodinámica |
|---|
 |
Un ciclo termodinámico consiste en secuencias enlazadas de procesos termodinámicos que implican transferencia de calor y trabajo dentro y fuera del sistema, mientras varían la presión, la temperatura y otras variables de estado dentro del sistema, y que eventualmente devuelven el sistema a su estado inicial. [1] En el proceso de pasar a través de un ciclo, el fluido de trabajo (sistema) puede convertir el calor de una fuente cálida en trabajo útil y disponer del calor restante en un sumidero frío, actuando así como un motor térmico . A la inversa, el ciclo puede invertirse y utilizar el trabajo para mover el calor de una fuente fría y transferirlo a un sumidero cálido, actuando así como una bomba de calor . Si en cada punto del ciclo el sistema está en equilibrio termodinámico , el ciclo es reversible. Ya sea que se lleve a cabo de forma reversible o irreversible, el cambio de entropía neta del sistema es cero, ya que la entropía es una función de estado .
Durante un ciclo cerrado, el sistema vuelve a su estado termodinámico original de temperatura y presión. Las magnitudes del proceso (o magnitudes de trayectoria), como el calor y el trabajo, dependen del proceso. En un ciclo en el que el sistema vuelve a su estado inicial, se aplica la primera ley de la termodinámica :
Lo anterior indica que no hay cambios en la energía interna ( ) del sistema durante el ciclo. representa el trabajo total y la entrada de calor durante el ciclo y sería el trabajo total y la salida de calor durante el ciclo. La naturaleza repetitiva de la trayectoria del proceso permite un funcionamiento continuo, lo que hace que el ciclo sea un concepto importante en termodinámica . Los ciclos termodinámicos a menudo se representan matemáticamente como procesos cuasiestáticos en el modelado del funcionamiento de un dispositivo real.
Calor y trabajo
Dos clases principales de ciclos termodinámicos son los ciclos de potencia y los ciclos de bomba de calor . Los ciclos de potencia son ciclos que convierten una parte de la entrada de calor en una salida de trabajo mecánico , mientras que los ciclos de bomba de calor transfieren calor de temperaturas bajas a altas utilizando trabajo mecánico como entrada. Los ciclos compuestos enteramente de procesos cuasiestáticos pueden funcionar como ciclos de potencia o de bomba de calor controlando la dirección del proceso. En un diagrama de presión-volumen (PV) o un diagrama de temperatura-entropía , las direcciones en sentido horario y antihorario indican ciclos de potencia y de bomba de calor, respectivamente.
Relación con el trabajo

Debido a que la variación neta en las propiedades de estado durante un ciclo termodinámico es cero, se forma un bucle cerrado en un diagrama PV . El eje Y de un diagrama PV muestra la presión ( P ) y el eje X muestra el volumen ( V ). El área encerrada por el bucle es el trabajo ( W ) realizado por el proceso:
Este trabajo es igual al balance de calor (Q) transferido al sistema:
La ecuación (2) es consistente con la Primera Ley; aunque la energía interna cambia durante el curso del proceso cíclico, cuando el proceso cíclico termina la energía interna del sistema es la misma que tenía cuando comenzó el proceso.
Si el proceso cíclico se mueve en el sentido de las agujas del reloj alrededor del bucle, entonces W será positivo y representará una máquina térmica . Si se mueve en el sentido contrario a las agujas del reloj, entonces W será negativo y representará una bomba de calor .
Una lista de procesos termodinámicos
Los siguientes procesos se utilizan a menudo para describir diferentes etapas de un ciclo termodinámico:
- Adiabático : No hay transferencia de energía en forma de calor (Q) durante esa parte del ciclo ( ). La transferencia de energía se considera únicamente como trabajo realizado por el sistema.
- Isotermal : el proceso se desarrolla a una temperatura constante durante esa parte del ciclo (T=constante ). La transferencia de energía se considera como calor extraído del sistema o trabajo realizado por éste.
- Isobárico : la presión en esa parte del ciclo permanecerá constante. (P = constante, ). La transferencia de energía se considera como calor extraído del sistema o trabajo realizado por el mismo.
- Isocórico : El proceso es de volumen constante (V=constante, ). La transferencia de energía se considera como calor extraído del sistema, ya que el trabajo realizado por el sistema es cero.
- Isentrópico : El proceso es de entropía constante (S=constante, ). Es adiabático (no hay intercambio de calor ni de masa) y reversible.
- Isentálpico : Proceso que se desarrolla sin ningún cambio en la entalpía o entalpía específica.
- Politrópico : Proceso que obedece a la relación .
- Reversible : Proceso donde la producción neta de entropía es cero; .
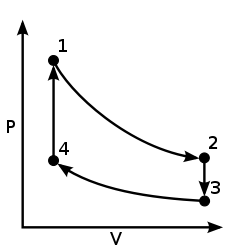
Ejemplo: El ciclo Otto

El ciclo Otto es un ejemplo de ciclo termodinámico reversible.
- 1→2: Expansión isentrópica / adiabática : Entropía constante (s), Disminución de la presión (P), Aumento del volumen (v), Disminución de la temperatura (T)
- 2→3: Enfriamiento isocórico : Volumen constante (v), Disminución de la presión (P), Disminución de la entropía (S), Disminución de la temperatura (T)
- 3→4: Compresión isentrópica/adiabática: Entropía constante (s), Aumento de presión (P), Disminución de volumen (v), Aumento de temperatura (T)
- 4→1: Calentamiento isocórico: Volumen constante (v), Aumento de la presión (P), Aumento de la entropía (S), Aumento de la temperatura (T)
Ciclos de energía

Los ciclos de potencia termodinámicos son la base del funcionamiento de los motores térmicos, que suministran la mayor parte de la energía eléctrica del mundo y hacen funcionar la gran mayoría de los vehículos de motor . Los ciclos de potencia se pueden organizar en dos categorías: ciclos reales y ciclos ideales. Los ciclos que se encuentran en los dispositivos del mundo real (ciclos reales) son difíciles de analizar debido a la presencia de efectos que los complican (fricción) y a la ausencia de tiempo suficiente para el establecimiento de las condiciones de equilibrio. Para fines de análisis y diseño, se crean modelos idealizados (ciclos ideales); estos modelos ideales permiten a los ingenieros estudiar los efectos de los principales parámetros que dominan el ciclo sin tener que dedicar un tiempo significativo a resolver los intrincados detalles presentes en el modelo del ciclo real.
Los ciclos de potencia también pueden dividirse según el tipo de motor térmico que buscan modelar. Los ciclos más comunes utilizados para modelar motores de combustión interna son el ciclo Otto , que modela motores de gasolina , y el ciclo Diesel , que modela motores diésel . Los ciclos que modelan motores de combustión externa incluyen el ciclo Brayton , que modela turbinas de gas , el ciclo Rankine , que modela turbinas de vapor , el ciclo Stirling , que modela motores de aire caliente , y el ciclo Ericsson , que también modela motores de aire caliente.

Por ejemplo: el trabajo mecánico de presión-volumen resultante del ciclo Stirling ideal (trabajo neto), que consta de 4 procesos termodinámicos, es [ cita requerida ] [ dudoso – discutir ] :
Para el ciclo Stirling ideal, no ocurre ningún cambio de volumen en los procesos 4-1 y 2-3, por lo que la ecuación (3) se simplifica a:
Ciclos de bomba de calor
Los ciclos de bomba de calor termodinámicos son los modelos para bombas de calor domésticas y refrigeradores . No hay diferencia entre los dos excepto que el propósito del refrigerador es enfriar un espacio muy pequeño mientras que la bomba de calor doméstica está destinada a calentar o enfriar una casa. Ambos funcionan moviendo calor de un espacio frío a un espacio cálido. El ciclo de refrigeración más común es el ciclo de compresión de vapor , que modela sistemas que utilizan refrigerantes que cambian de fase. El ciclo de refrigeración por absorción es una alternativa que absorbe el refrigerante en una solución líquida en lugar de evaporarlo. Los ciclos de refrigeración de gas incluyen el ciclo Brayton invertido y el ciclo Hampson-Linde . Los ciclos de compresión y expansión múltiples permiten que los sistemas de refrigeración de gas licúen los gases .
Modelado de sistemas reales
 |
Los ciclos termodinámicos se pueden utilizar para modelar dispositivos y sistemas reales, generalmente haciendo una serie de suposiciones. [2] A menudo es necesario simplificar las suposiciones para reducir el problema a una forma más manejable. [2] Por ejemplo, como se muestra en la figura, los dispositivos como una turbina de gas o un motor a reacción se pueden modelar como un ciclo Brayton . El dispositivo real está formado por una serie de etapas, cada una de las cuales se modela como un proceso termodinámico idealizado. Aunque cada etapa que actúa sobre el fluido de trabajo es un dispositivo real complejo, se pueden modelar como procesos idealizados que se aproximan a su comportamiento real. Si se agrega energía por otros medios que no sean la combustión, entonces una suposición adicional es que los gases de escape pasarían desde el escape a un intercambiador de calor que hundiría el calor residual al medio ambiente y el gas de trabajo se reutilizaría en la etapa de entrada.
La diferencia entre un ciclo idealizado y el rendimiento real puede ser significativa. [2] Por ejemplo, las siguientes imágenes ilustran las diferencias en el trabajo de salida previsto por un ciclo Stirling ideal y el rendimiento real de un motor Stirling:
 |  |  |
| Ciclo Stirling ideal | Rendimiento real | Superposición de lo real y lo ideal, que muestra la diferencia en el rendimiento laboral |
Como el resultado neto de trabajo de un ciclo está representado por el interior del ciclo, existe una diferencia significativa entre el resultado de trabajo previsto del ciclo ideal y el resultado de trabajo real que muestra un motor real. También se puede observar que los procesos individuales reales difieren de sus contrapartes idealizadas; por ejemplo, la expansión isocórica (proceso 1-2) ocurre con algún cambio de volumen real.
Ciclos termodinámicos conocidos
En la práctica, los ciclos termodinámicos idealizados simples suelen estar formados por cuatro procesos termodinámicos . Se puede utilizar cualquier proceso termodinámico. Sin embargo, cuando se modelan ciclos idealizados, a menudo se utilizan procesos en los que una variable de estado se mantiene constante, como:
- adiabático (calor constante)
- isotérmico (temperatura constante)
- isobárico (presión constante)
- isocórico (volumen constante)
- isentrópico (entropía constante)
- isentálpico (entalpía constante)
Algunos ejemplos de ciclos termodinámicos y sus procesos constituyentes son los siguientes:
| Ciclo | Compresión, 1→2 | Adición de calor, 2→3 | Expansión, 3→4 | Rechazo de calor, 4→1 | Notas |
|---|---|---|---|---|---|
| Ciclos de potencia normalmente con combustión externa - o ciclos de bomba de calor: | |||||
| Campana Coleman | adiabático | isobárico | adiabático | isobárico | Un ciclo Brayton invertido |
| Carnot | isentrópico | isotérmico | isentrópico | isotérmico | Motor térmico de Carnot |
| Ericsson | isotérmico | isobárico | isotérmico | isobárico | El segundo ciclo de Ericsson de 1853 |
| Rankine | adiabático | isobárico | adiabático | isobárico | Máquinas de vapor |
| Higroscópico | adiabático | isobárico | adiabático | isobárico | |
| Escuderos | adiabático | Presión y volumen variables | adiabático | isocórico | |
| Stirling | isotérmico | isocórico | isotérmico | isocórico | Motores Stirling |
| Manson | isotérmico | isocórico | isotérmico | isocórico luego adiabático | Motores Manson y Manson-Guise |
| Stoddard | adiabático | isobárico | adiabático | isobárico | |
| Ciclos de potencia normales con combustión interna : | |||||
| Atkinson | isentrópico | isocórico | isentrópico | isocórico | Se diferencia del ciclo Otto en que V 1 < V 4 . |
| Brayton | adiabático | isobárico | adiabático | isobárico | Estatorreactores , turborreactores , hélices y ejes . Originalmente desarrollados para su uso en motores alternativos. La versión de combustión externa de este ciclo se conoce como el primer ciclo Ericsson de 1833. |
| Diesel | adiabático | isobárico | adiabático | isocórico | Motor diésel |
| Humphrey | isentrópico | isocórico | isentrópico | isobárico | Shcramjets , motores de detonación pulsada y continua |
| Lenoir | isocórico | adiabático | isobárico | Pulso-chorros . 1→2 logra tanto la disipación de calor como la compresión. Originalmente desarrollado para su uso en motores alternativos. | |
| Otón | isentrópico | isocórico | isentrópico | isocórico | Motores de gasolina/gasolina |
Ciclo ideal

Un ciclo ideal es sencillo de analizar y consta de:
- PARTE SUPERIOR (A) y PARTE INFERIOR (C) del bucle: un par de procesos isobáricos paralelos
- DERECHA (B) e IZQUIERDA (D) del bucle: un par de procesos isocóricos paralelos
Si la sustancia activa es un gas perfecto , es solo una función de para un sistema cerrado ya que su presión interna se anula. Por lo tanto, los cambios de energía interna de un gas perfecto que experimenta varios procesos que conectan el estado inicial con el estado final siempre están dados por la fórmula
Suponiendo que es constante, para cualquier proceso experimentado por un gas perfecto.
Bajo este conjunto de supuestos, para los procesos A y C tenemos y , mientras que para los procesos B y D tenemos y .
El trabajo total realizado por ciclo es , que es simplemente el área del rectángulo. Si se requiere el flujo de calor total por ciclo, esto se obtiene fácilmente. Como , tenemos .
De esta forma, el flujo de calor total por ciclo se calcula sin conocer las capacidades térmicas y los cambios de temperatura para cada paso (aunque esta información sería necesaria para evaluar la eficiencia termodinámica del ciclo).
Ciclo de Carnot
El ciclo de Carnot es un ciclo compuesto por procesos totalmente reversibles de compresión y expansión isentrópica y adición y eliminación de calor isotérmico . La eficiencia térmica de un ciclo de Carnot depende únicamente de las temperaturas absolutas de los dos reservorios en los que tiene lugar la transferencia de calor, y para un ciclo de potencia es:
donde es la temperatura más baja del ciclo y la más alta. Para los ciclos de potencia de Carnot, el coeficiente de rendimiento de una bomba de calor es:
y para un refrigerador el coeficiente de rendimiento es:
La segunda ley de la termodinámica limita la eficiencia y el coeficiente de rendimiento de todos los dispositivos cíclicos a niveles iguales o inferiores a la eficiencia de Carnot. El ciclo Stirling y el ciclo Ericsson son otros dos ciclos reversibles que utilizan la regeneración para obtener transferencia de calor isotérmica.
Ciclo Stirling
Un ciclo Stirling es como un ciclo Otto, excepto que las adiabáticas se sustituyen por isotermas. También es igual que un ciclo Ericsson, en el que los procesos isobáricos se sustituyen por procesos de volumen constante.
- PARTE SUPERIOR e INFERIOR del bucle: un par de procesos isotérmicos cuasi paralelos
- Lados IZQUIERDO y DERECHO del bucle: un par de procesos isocóricos paralelos
El calor fluye hacia el interior del circuito a través de la isoterma superior y la isocora izquierda, y parte de este calor fluye de regreso hacia afuera a través de la isoterma inferior y la isocora derecha, pero la mayor parte del flujo de calor se produce a través del par de isotermas. Esto tiene sentido, ya que todo el trabajo realizado por el ciclo lo realizan el par de procesos isotérmicos, que se describen mediante Q=W . Esto sugiere que todo el calor neto entra a través de la isoterma superior. De hecho, todo el calor que entra a través de la isocora izquierda sale a través de la isocora derecha: dado que la isoterma superior está toda a la misma temperatura más cálida y la isoterma inferior está toda a la misma temperatura más fría , y dado que el cambio de energía para una isocora es proporcional al cambio de temperatura, entonces todo el calor que entra a través de la isocora izquierda se cancela exactamente por el calor que sale por la isocora derecha.
Funciones de estado y entropía
Si Z es una función de estado , entonces el equilibrio de Z permanece sin cambios durante un proceso cíclico:
- .
La entropía es una función de estado y se define en sentido absoluto a través de la Tercera Ley de la Termodinámica como
donde se elige un camino reversible desde el cero absoluto hasta el estado final, de modo que para un proceso reversible isotérmico
- .
En general, para cualquier proceso cíclico los puntos de estado se pueden conectar mediante caminos reversibles, de modo que
lo que significa que el cambio neto de entropía del fluido de trabajo durante un ciclo es cero.
Véase también
Referencias
- ^ Cengel, Yunus A.; Boles, Michael A. (2002). Termodinámica: un enfoque de ingeniería . Boston: McGraw-Hill. pp. 14. ISBN 0-07-238332-1.
- ^ abc Cengel, Yunus A.; Boles, Michael A. (2002). Termodinámica: un enfoque de ingeniería. Boston: McGraw-Hill. pp. 452. ISBN 0-07-238332-1 .
Lectura adicional
- Halliday, Resnick y Walker. Fundamentos de física , 5.ª edición. John Wiley & Sons, 1997. Capítulo 21, Entropía y segunda ley de la termodinámica .
- Çengel, Yunus A., y Michael A. Boles. Termodinámica: un enfoque de ingeniería , 7.ª ed. Nueva York: McGraw-Hill, 2011. Impreso.
- Hill y Peterson. "Mecánica y termodinámica de la propulsión", 2.ª ed. Prentice Hall, 1991. 760 págs.


























































