Nucleación

Termodinámica
La clásica máquina térmica de Carnot
Sucursales Clásico Estadístico Químico Termodinámica cuántica Equilibrio  / No equilibrio
Leyes Cero Primero Segundo Tercero
Sistemas Sistema cerrado Sistema abierto Sistema aislado Estado Ecuación de estado Gas ideal Gas real Estado de la materia Fase (materia) Equilibrio Controlar el volumen Instrumentos Procesos Isobárico Isocórico Isotermal Adiabático Isentrópico Isentálpico Cuasistático Politrópico Expansión libre Reversibilidad Irreversibilidad Endorreversibilidad Ciclos Motores térmicos Bombas de calor Eficiencia térmica
Propiedades del sistema Nota: Variables conjugadas en cursiva Diagramas de propiedades Propiedades intensivas y extensivas Funciones del proceso Trabajar Calor Funciones del estado Temperatura  / Entropía  ( introducción ) Presión  / Volumen Potencial químico  / Número de partículas Calidad del vapor Propiedades reducidas
Propiedades del material Bases de datos de propiedades Capacidad calorífica específica  ${\estilo de visualización c=}$ ${\estilo de visualización T}$ ${\displaystyle \s parcial}$ ${\estilo de visualización N}$ ${\displaystyle \parcial T}$ Compresibilidad  ${\displaystyle \beta =-}$ ${\estilo de visualización 1}$ ${\displaystyle \V parcial}$ ${\estilo de visualización V}$ ${\displaystyle \p parcial}$ Expansión térmica  ${\displaystyle \alpha =}$ ${\estilo de visualización 1}$ ${\displaystyle \V parcial}$ ${\estilo de visualización V}$ ${\displaystyle \parcial T}$
Ecuaciones Teorema de Carnot Teorema de Clausius Relación fundamental Ley de los gases ideales Relaciones de Maxwell Relaciones recíprocas de Onsager Ecuaciones de Bridgman Tabla de ecuaciones termodinámicas
Potenciales Energía libre Entropía libre Energía interna ${\displaystyle U(S,V)}$ Entalpía ${\displaystyle H(S,p)=U+pV}$ Energía libre de Helmholtz ${\displaystyle A(T,V)=U-TS}$ Energía libre de Gibbs ${\displaystyle G(T,p)=H-TS}$
Historia Cultura Historia General Entropía Leyes de los gases Máquinas de "movimiento perpetuo" Filosofía Entropía y tiempo Entropía y vida Trinquete browniano El demonio de Maxwell Paradoja de la muerte por calor La paradoja de Loschmidt Sinergética Teorías Teoría calórica Vis viva ("fuerza viva") Equivalente mecánico del calor Fuerza motriz Publicaciones clave Una investigación sobre la fuente... la fricción Sobre el equilibrio de sustancias heterogéneas Reflexiones sobre la fuerza motriz del fuego Timelines Thermodynamics Heat engines Art Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Boltzmann Bridgman Carathéodory Carnot Clapeyron Clausius de Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

En termodinámica , la nucleación es el primer paso en la formación de una nueva fase o estructura termodinámica a través del autoensamblaje o la autoorganización dentro de una sustancia o mezcla . La nucleación se define típicamente como el proceso que determina cuánto tiempo tiene que esperar un observador antes de que aparezca la nueva fase o estructura autoorganizada. Por ejemplo, si un volumen de agua se enfría (a presión atmosférica ) significativamente por debajo de 0  °C, tenderá a congelarse en hielo , pero los volúmenes de agua enfriados solo unos pocos grados por debajo de 0  °C a menudo permanecen completamente libres de hielo durante largos períodos ( sobreenfriamiento ). En estas condiciones, la nucleación del hielo es lenta o no ocurre en absoluto. Sin embargo, a temperaturas más bajas, la nucleación es rápida y los cristales de hielo aparecen después de poco o ningún retraso. ^{[1] [2]}

La nucleación es un mecanismo común que genera transiciones de fase de primer orden y es el inicio del proceso de formación de una nueva fase termodinámica. Por el contrario, las nuevas fases en transiciones de fase continuas comienzan a formarse inmediatamente.

La nucleación suele ser muy sensible a las impurezas del sistema. Estas impurezas pueden ser demasiado pequeñas para ser vistas a simple vista, pero aun así pueden controlar la velocidad de nucleación. Por ello, suele ser importante distinguir entre nucleación heterogénea y nucleación homogénea. La nucleación heterogénea se produce en los sitios de nucleación de las superficies del sistema. ^[1] La nucleación homogénea se produce lejos de una superficie.

La nucleación es generalmente un proceso estocástico (aleatorio), por lo que incluso en dos sistemas idénticos la nucleación ocurrirá en momentos diferentes. ^{[1] [2] [3] [4]} Un mecanismo común se ilustra en la animación de la derecha. Esta muestra la nucleación de una nueva fase (mostrada en rojo) en una fase existente (blanca). En la fase existente aparecen fluctuaciones microscópicas de la fase roja y decaen continuamente, hasta que una fluctuación inusualmente grande de la nueva fase roja es tan grande que es más favorable para ella crecer que contraerse hasta la nada. Este núcleo de la fase roja crece entonces y convierte el sistema a esta fase. La teoría estándar que describe este comportamiento para la nucleación de una nueva fase termodinámica se llama teoría clásica de nucleación . Sin embargo, la CNT falla en la descripción de los resultados experimentales de nucleación de vapor a líquido incluso para sustancias modelo como el argón por varios órdenes de magnitud. ^[5]

Para la nucleación de una nueva fase termodinámica, como la formación de hielo en agua por debajo de 0  °C, si el sistema no evoluciona con el tiempo y la nucleación ocurre en un solo paso, entonces la probabilidad de que la nucleación no haya ocurrido debería sufrir una desintegración exponencial . Esto se ve, por ejemplo, en la nucleación de hielo en pequeñas gotas de agua superenfriadas . ^[6] La tasa de desintegración exponencial da la tasa de nucleación. La teoría clásica de la nucleación es una teoría aproximada ampliamente utilizada para estimar estas tasas y cómo varían con variables como la temperatura. Predice correctamente que el tiempo que hay que esperar para la nucleación disminuye extremadamente rápido cuando está sobresaturada . ^{[1] [2] [4]}

No son solo las nuevas fases, como líquidos y cristales, las que se forman mediante la nucleación seguida de crecimiento. El proceso de autoensamblaje que forma objetos como los agregados amiloides asociados con la enfermedad de Alzheimer también comienza con la nucleación. ^[7] Los sistemas autoorganizados que consumen energía, como los microtúbulos en las células, también muestran nucleación y crecimiento.

La nucleación heterogénea, es decir, la nucleación con el núcleo en una superficie, es mucho más común que la nucleación homogénea. ^{[1] [3]} Por ejemplo, en la nucleación de hielo a partir de gotitas de agua superenfriada, la purificación del agua para eliminar todas o casi todas las impurezas da como resultado gotitas de agua que se congelan a temperaturas inferiores a -35  °C, ^{[1] [3] [6]} mientras que el agua que contiene impurezas puede congelarse a -5  °C o más. ^[1]

Esta observación de que la nucleación heterogénea puede ocurrir cuando la tasa de nucleación homogénea es esencialmente cero, se entiende a menudo utilizando la teoría de nucleación clásica . Esta predice que la nucleación se ralentiza exponencialmente con la altura de una barrera de energía libre ΔG*. Esta barrera proviene de la penalización de energía libre de formar la superficie del núcleo en crecimiento. Para la nucleación homogénea, el núcleo se aproxima por una esfera, pero como podemos ver en el esquema de gotas macroscópicas a la derecha, las gotas en las superficies no son esferas completas y, por lo tanto, el área de la interfaz entre la gota y el fluido circundante es menor que la de una esfera . Esta reducción en el área de superficie del núcleo reduce la altura de la barrera a la nucleación y, por lo tanto, acelera la nucleación exponencialmente. ^[2]${\displaystyle 4\pi r^{2}}$

La nucleación también puede comenzar en la superficie de un líquido. Por ejemplo, las simulaciones por computadora de nanopartículas de oro muestran que la fase cristalina a veces se nuclea en la superficie del oro líquido. ^[8]

La teoría clásica de la nucleación parte de una serie de supuestos; por ejemplo, trata un núcleo microscópico como si fuera una gota macroscópica con una superficie bien definida cuya energía libre se calcula utilizando una propiedad de equilibrio: la tensión interfacial σ. En el caso de un núcleo que puede tener tan solo diez moléculas de diámetro, no siempre resulta claro que podamos tratar algo tan pequeño como un volumen más una superficie. Además, la nucleación es un fenómeno inherentemente fuera del equilibrio termodinámico , por lo que no siempre resulta obvio que su velocidad pueda estimarse utilizando propiedades de equilibrio.

Sin embargo, las computadoras modernas son lo suficientemente potentes como para calcular tasas de nucleación esencialmente exactas para modelos simples. Estas se han comparado con la teoría clásica, por ejemplo para el caso de la nucleación de la fase cristalina en el modelo de esferas duras. Este es un modelo de esferas perfectamente duras en movimiento térmico, y es un modelo simple de algunos coloides . Para la cristalización de esferas duras, la teoría clásica es una teoría aproximada muy razonable. ^[9] Por lo tanto, para los modelos simples que podemos estudiar, la teoría de nucleación clásica funciona bastante bien, pero no sabemos si funciona igualmente bien para (por ejemplo) moléculas complejas que cristalizan a partir de una solución.

Los procesos de transición de fase también se pueden explicar en términos de descomposición espinodal , donde la separación de fases se retrasa hasta que el sistema entra en la región inestable donde una pequeña perturbación en la composición conduce a una disminución de la energía y, por lo tanto, al crecimiento espontáneo de la perturbación. ^[10] Esta región de un diagrama de fases se conoce como región espinodal y el proceso de separación de fases se conoce como descomposición espinodal y puede estar regido por la ecuación de Cahn-Hilliard .

En muchos casos, los líquidos y las soluciones se pueden enfriar o concentrar hasta condiciones en las que el líquido o la solución son significativamente menos estables termodinámicamente que el cristal, pero donde no se formarán cristales durante minutos, horas, semanas o más; este proceso se llama superenfriamiento . La nucleación del cristal se evita entonces mediante una barrera sustancial. Esto tiene consecuencias, por ejemplo, las nubes frías a gran altitud pueden contener grandes cantidades de pequeñas gotas de agua líquida que están muy por debajo de los 0  °C.

En volúmenes pequeños, como en gotas pequeñas, puede que solo se necesite un evento de nucleación para la cristalización. En estos volúmenes pequeños, el tiempo hasta que aparece el primer cristal suele definirse como el tiempo de nucleación. La nucleación de cristales de carbonato de calcio depende no solo del grado de sobresaturación, sino también de la relación entre iones de calcio y de carbonato en soluciones acuosas. ^[11] En volúmenes mayores, se producirán muchos eventos de nucleación. Un modelo simple para la cristalización en ese caso, que combina nucleación y crecimiento, es el modelo KJMA o de Avrami .

Aunque las teorías existentes, incluida la teoría clásica de nucleación, explican bien el estado de nucleación estable cuando la tasa de nucleación de los cristales no depende del tiempo, la nucleación transitoria inicial en estado no estable ^[12] y el período de incubación aún más misterioso requieren más atención de la comunidad científica. Se sugirió que el ordenamiento químico del líquido de subenfriamiento antes de la nucleación de los cristales era responsable de esa característica ^[13] al reducir la barrera energética para la nucleación. ^[14]

El tiempo transcurrido hasta la aparición del primer cristal también se denomina tiempo de nucleación primaria, para distinguirlo de los tiempos de nucleación secundaria. En este caso, el término primario se refiere al primer núcleo que se forma, mientras que los núcleos secundarios son núcleos de cristal producidos a partir de un cristal preexistente. La nucleación primaria describe la transición a una nueva fase que no depende de que la nueva fase ya esté presente, ya sea porque es el primer núcleo de esa fase que se forma o porque el núcleo se forma lejos de cualquier pieza preexistente de la nueva fase. En particular, en el estudio de la cristalización, la nucleación secundaria puede ser importante. Se trata de la formación de núcleos de un nuevo cristal causada directamente por cristales preexistentes. ^[15]

Por ejemplo, si los cristales están en una solución y el sistema está sujeto a fuerzas de cizallamiento, se podrían desprender pequeños núcleos de cristales de un cristal en crecimiento, aumentando así el número de cristales en el sistema. Por lo tanto, tanto la nucleación primaria como la secundaria aumentan el número de cristales en el sistema, pero sus mecanismos son muy diferentes y la nucleación secundaria depende de que los cristales ya estén presentes.

Normalmente es difícil estudiar experimentalmente la nucleación de los cristales. El núcleo es microscópico y, por lo tanto, demasiado pequeño para ser observado directamente. En grandes volúmenes de líquido, normalmente hay múltiples eventos de nucleación y es difícil separar los efectos de la nucleación de los del crecimiento de la fase nucleada. Estos problemas se pueden superar trabajando con gotas pequeñas. Como la nucleación es estocástica , se necesitan muchas gotas para poder obtener estadísticas de los eventos de nucleación.

A la derecha se muestra un ejemplo de conjunto de datos de nucleación. Se trata de la nucleación a temperatura constante y, por lo tanto, de la sobresaturación de la fase cristalina en pequeñas gotas de estaño líquido superenfriado; este es el trabajo de Pound y La Mer. ^[16]

La nucleación se produce en diferentes gotitas en diferentes momentos, por lo que la fracción no es una función escalonada simple que cae bruscamente de uno a cero en un momento particular. La curva roja es un ajuste de una función de Gompertz a los datos. Esta es una versión simplificada del modelo que Pound y La Mer usaron para modelar sus datos. ^[16] El modelo supone que la nucleación se produce debido a partículas de impureza en las gotitas de estaño líquido, y hace la suposición simplificadora de que todas las partículas de impureza producen nucleación a la misma velocidad. También supone que estas partículas están distribuidas por Poisson entre las gotitas de estaño líquido. Los valores de ajuste son que la tasa de nucleación debido a una sola partícula de impureza es 0,02/s, y el número promedio de partículas de impureza por gotita es 1,2. Nótese que alrededor del 30% de las gotitas de estaño nunca se congelan; los datos se estabilizan en una fracción de aproximadamente 0,3. En el modelo se supone que esto se debe a que, por casualidad, estas gotitas no tienen ni una sola partícula de impureza y, por lo tanto, no hay nucleación heterogénea. Se supone que la nucleación homogénea es insignificante en la escala de tiempo de este experimento. Las gotitas restantes se congelan de forma estocástica, a velocidades de 0,02/s si tienen una partícula de impureza, 0,04/s si tienen dos, y así sucesivamente.

Estos datos son sólo un ejemplo, pero ilustran características comunes de la nucleación de cristales en el sentido de que hay evidencia clara de nucleación heterogénea y que la nucleación es claramente estocástica.

La congelación de pequeñas gotas de agua en forma de hielo es un proceso importante, en particular en la formación y dinámica de las nubes. ^[1] El agua (a presión atmosférica) no se congela a 0  °C, sino a temperaturas que tienden a disminuir a medida que disminuye el volumen del agua y aumenta la concentración de sustancias químicas disueltas en el agua. ^[1]

Así, pequeñas gotas de agua, como las que se encuentran en las nubes, pueden permanecer líquidas mucho más allá de los 0  °C.

A la derecha se muestra un ejemplo de datos experimentales sobre la congelación de pequeñas gotas de agua. El gráfico muestra la fracción de un gran conjunto de gotas de agua que todavía son agua líquida, es decir, que aún no se han congelado, en función de la temperatura. Nótese que la temperatura más alta a la que cualquiera de las gotas se congela está cerca de los -19  °C, mientras que la última gota en congelarse lo hace a casi -35  °C. ^[17]

• Las nubes se forman cuando el aire húmedo se enfría (a menudo porque el aire se eleva ) y muchas pequeñas gotas de agua se nuclean a partir del aire sobresaturado. ^[1] La cantidad de vapor de agua que el aire puede transportar disminuye con temperaturas más bajas . El exceso de vapor comienza a nuclearse y a formar pequeñas gotas de agua que forman una nube. La nucleación de las gotas de agua líquida es heterogénea y se produce en partículas denominadas núcleos de condensación de nubes . La siembra de nubes es el proceso de agregar núcleos de condensación artificiales para acelerar la formación de nubes.
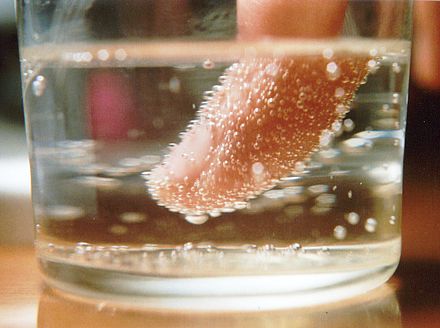
• Las burbujas de dióxido de carbono se nuclean poco después de que se libera la presión de un recipiente con líquido carbonatado .
• La nucleación en ebullición puede ocurrir en el líquido a granel si se reduce la presión de modo que el líquido se sobrecaliente con respecto al punto de ebullición dependiente de la presión. Más a menudo, la nucleación ocurre en la superficie de calentamiento, en los sitios de nucleación. Por lo general, los sitios de nucleación son pequeñas grietas donde se mantiene la superficie libre de gas-líquido o puntos en la superficie de calentamiento con propiedades de humectación inferiores . Se puede lograr un sobrecalentamiento sustancial de un líquido después de que el líquido se desgasifique y si las superficies de calentamiento están limpias, lisas y hechas de materiales bien humectados por el líquido.
• Algunos agitadores de champán funcionan proporcionando muchos sitios de nucleación a través de una gran superficie y esquinas afiladas, lo que acelera la liberación de burbujas y elimina la carbonatación del vino.
• La erupción de la Coca-Cola Light y los caramelos Mentos es otro ejemplo. La superficie de los caramelos Mentos proporciona puntos de nucleación para la formación de burbujas de dióxido de carbono a partir de refrescos carbonatados.
• Tanto la cámara de burbujas como la cámara de nubes dependen de la nucleación de burbujas y gotas, respectivamente.

• El proceso de cristalización más común en la Tierra es la formación de hielo. El agua líquida no se congela a 0  °C a menos que ya haya hielo presente;  se requiere un enfriamiento significativo por debajo de 0 °C para que se nuclee el hielo y el agua se congele. Por ejemplo, pequeñas gotas de agua muy pura pueden permanecer líquidas hasta por debajo de los -30 °C, aunque el hielo es el estado estable por debajo de 0  °C. ^[1]
• Muchos de los materiales que fabricamos y utilizamos son cristalinos, pero están hechos de líquidos, por ejemplo, el hierro cristalino está hecho de hierro líquido fundido en un molde, por lo que la nucleación de materiales cristalinos se estudia ampliamente en la industria. ^[18] Se utiliza mucho en la industria química para casos como la preparación de polvos ultradispersos metálicos que pueden servir como catalizadores. Por ejemplo, el platino depositado sobre nanopartículas de TiO ₂ cataliza la descomposición del agua. ^[19] Es un factor importante en la industria de semiconductores, ya que la energía de la brecha de banda en los semiconductores está influenciada por el tamaño de los nanocúmulos. ^[20]

Además de la nucleación y el crecimiento de cristales, por ejemplo, en vidrios no cristalinos, la nucleación y el crecimiento de precipitados de impurezas en cristales en y entre los límites de grano es bastante importante a nivel industrial. Por ejemplo, en los metales, la nucleación en estado sólido y el crecimiento de precipitados desempeñan un papel importante, por ejemplo, en la modificación de propiedades mecánicas como la ductilidad, mientras que en los semiconductores desempeñan un papel importante, por ejemplo, en la captura de impurezas durante la fabricación de circuitos integrados. ^[21]