Motor térmico

Termodinámica
La clásica máquina térmica de Carnot
Sucursales Clásico Estadístico Químico Termodinámica cuántica Equilibrio  / No equilibrio
Leyes Cero Primero Segundo Tercero
Sistemas Sistema cerrado Sistema abierto Sistema aislado Estado Ecuación de estado Gas ideal Gas real Estado de la materia Fase (materia) Equilibrio Controlar el volumen Instrumentos Procesos Isobárico Isocórico Isotermal Adiabático Isentrópico Isentálpico Cuasistático Politrópico Expansión libre Reversibilidad Irreversibilidad Endorreversibilidad Ciclos Heat engines Heat pumps Thermal efficiency
System properties Note: Conjugate variables in italics Property diagrams Intensive and extensive properties Process functions Work Heat Functions of state Temperature / Entropy (introduction) Pressure / Volume Chemical potential / Particle number Vapor quality Reduced properties
Material properties Property databases Specific heat capacity  ${\displaystyle c=}$ ${\displaystyle T}$ ${\displaystyle \partial S}$ ${\displaystyle N}$ ${\displaystyle \partial T}$ Compressibility  ${\displaystyle \beta =-}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial p}$ Thermal expansion  ${\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial T}$
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Onsager reciprocal relations Bridgman's equations Table of thermodynamic equations
Potentials Free energy Free entropy Internal energy ${\displaystyle U(S,V)}$ Enthalpy ${\displaystyle H(S,p)=U+pV}$ Helmholtz free energy ${\displaystyle A(T,V)=U-TS}$ Gibbs free energy ${\displaystyle G(T,p)=H-TS}$
History Culture History General Entropy Gas laws "Perpetual motion" machines Philosophy Entropy and time Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics Theories Caloric theory Vis viva ("living force") Mechanical equivalent of heat Motive power Key publications An Inquiry Concerning the Source ... Friction On the Equilibrium of Heterogeneous Substances Reflections on the Motive Power of Fire Timelines Thermodynamics Heat engines Art Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Boltzmann Bridgman Carathéodory Carnot Clapeyron Clausius de Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

Un motor térmico es un sistema que convierte el calor en energía utilizable , particularmente energía mecánica , que luego puede usarse para realizar trabajo mecánico . ^{[1] [2]} Si bien originalmente se concibió en el contexto de la energía mecánica, el concepto de motor térmico se ha aplicado a varios otros tipos de energía, particularmente la eléctrica , desde al menos fines del siglo XIX. ^{[3] [4]} El motor térmico hace esto al llevar una sustancia de trabajo de una temperatura de estado más alta a una temperatura de estado más baja. Una fuente de calor genera energía térmica que lleva la sustancia de trabajo al estado de temperatura más alta. La sustancia de trabajo genera trabajo en el cuerpo de trabajo del motor mientras transfiere calor al disipador más frío hasta que alcanza un estado de temperatura más baja. Durante este proceso, parte de la energía térmica se convierte en trabajo al explotar las propiedades de la sustancia de trabajo. La sustancia de trabajo puede ser cualquier sistema con una capacidad térmica distinta de cero , pero generalmente es un gas o un líquido. Durante este proceso, normalmente se pierde algo de calor al entorno y no se convierte en trabajo. Además, parte de la energía es inutilizable debido a la fricción y la resistencia .

En general, un motor es cualquier máquina que convierte energía en trabajo mecánico . Los motores térmicos se distinguen de otros tipos de motores por el hecho de que su eficiencia está limitada fundamentalmente por el teorema de la termodinámica de Carnot . ^[5] Aunque esta limitación de la eficiencia puede ser un inconveniente, una ventaja de los motores térmicos es que la mayoría de las formas de energía se pueden convertir fácilmente en calor mediante procesos como reacciones exotérmicas (como la combustión), fisión nuclear , absorción de luz o partículas energéticas, fricción , disipación y resistencia . Dado que la fuente de calor que suministra energía térmica al motor puede ser alimentada por prácticamente cualquier tipo de energía, los motores térmicos cubren una amplia gama de aplicaciones.

Los motores térmicos suelen confundirse con los ciclos que intentan implementar. Normalmente, el término "motor" se utiliza para referirse a un dispositivo físico y "ciclo" para referirse a los modelos.

En termodinámica , los motores térmicos suelen modelarse utilizando un modelo de ingeniería estándar, como el ciclo Otto . El modelo teórico se puede refinar y aumentar con datos reales de un motor en funcionamiento, utilizando herramientas como un diagrama de indicadores . Dado que muy pocas implementaciones reales de motores térmicos coinciden exactamente con sus ciclos termodinámicos subyacentes, se podría decir que un ciclo termodinámico es un caso ideal de un motor mecánico. En cualquier caso, comprender plenamente un motor y su eficiencia requiere una buena comprensión del modelo teórico (posiblemente simplificado o idealizado), los matices prácticos de un motor mecánico real y las discrepancias entre ambos.

En términos generales, cuanto mayor sea la diferencia de temperatura entre la fuente caliente y el sumidero frío, mayor será la eficiencia térmica potencial del ciclo. En la Tierra, el lado frío de cualquier motor térmico está limitado a estar cerca de la temperatura ambiente del entorno, o no mucho más bajo que 300 kelvin , por lo que la mayoría de los esfuerzos para mejorar las eficiencias termodinámicas de varios motores térmicos se centran en aumentar la temperatura de la fuente, dentro de los límites materiales. La eficiencia teórica máxima de un motor térmico (que ningún motor alcanza nunca) es igual a la diferencia de temperatura entre los extremos caliente y frío dividida por la temperatura en el extremo caliente, cada una expresada en temperatura absoluta .

La eficiencia de los diversos motores térmicos propuestos o utilizados en la actualidad varía mucho:

• 3% ^[6] (97 por ciento de calor residual utilizando calor de baja calidad) para la propuesta de energía oceánica de conversión de energía térmica oceánica (OTEC)
• 25% para la mayoría de los motores de gasolina para automóviles ^[7]
• 49% para una central eléctrica de carbón supercrítico como la central eléctrica de Avedøre
• 60% para una turbina de gas de ciclo combinado ^[8]

La eficiencia de estos procesos es aproximadamente proporcional a la caída de temperatura a través de ellos. Los equipos auxiliares, como las bombas, pueden consumir una cantidad significativa de energía, lo que reduce efectivamente la eficiencia.

Aunque algunos ciclos tienen una ubicación de combustión típica (interna o externa), a menudo se pueden implementar con el otro. Por ejemplo, John Ericsson ^[9] desarrolló un motor calentado externamente que funciona en un ciclo muy similar al ciclo Diesel anterior . Además, los motores calentados externamente a menudo se pueden implementar en ciclos abiertos o cerrados. En un ciclo cerrado, el fluido de trabajo se retiene dentro del motor al completarse el ciclo, mientras que en un ciclo abierto, el fluido de trabajo se intercambia con el medio ambiente junto con los productos de la combustión en el caso del motor de combustión interna o simplemente se ventila al medio ambiente en el caso de los motores de combustión externa como los motores de vapor y las turbinas .

Ejemplos cotidianos de motores térmicos incluyen la central térmica , el motor de combustión interna , las armas de fuego , los refrigeradores y las bombas de calor . Las centrales eléctricas son ejemplos de motores térmicos que funcionan en dirección hacia adelante en el que el calor fluye desde un depósito caliente y fluye hacia un depósito frío para producir trabajo como producto deseado. Los refrigeradores, los acondicionadores de aire y las bombas de calor son ejemplos de motores térmicos que funcionan en sentido inverso, es decir, utilizan trabajo para tomar energía térmica a baja temperatura y elevar su temperatura de una manera más eficiente que la simple conversión de trabajo en calor (ya sea a través de fricción o resistencia eléctrica). Los refrigeradores extraen calor de dentro de una cámara sellada térmicamente a baja temperatura y ventilan el calor residual a una temperatura más alta al medio ambiente y las bombas de calor toman calor del entorno de baja temperatura y lo "ventilan" a una cámara sellada térmicamente (una casa) a mayor temperatura.

En general, los motores térmicos explotan las propiedades térmicas asociadas con la expansión y compresión de los gases de acuerdo con las leyes de los gases o las propiedades asociadas con los cambios de fase entre los estados gaseoso y líquido.

La atmósfera y la hidrosfera de la Tierra (el motor térmico de la Tierra) son procesos acoplados que compensan constantemente los desequilibrios del calentamiento solar a través de la evaporación del agua superficial, la convección, las precipitaciones, los vientos y la circulación oceánica, al distribuir el calor alrededor del globo. ^[10]

Una célula de Hadley es un ejemplo de motor térmico. Implica el ascenso de aire cálido y húmedo en la región ecuatorial de la Tierra y el descenso de aire más frío en las zonas subtropicales, lo que crea una circulación directa impulsada térmicamente, con la consiguiente producción neta de energía cinética. ^[11]

En los ciclos de cambio de fase y en los motores, los fluidos de trabajo son gases y líquidos. El motor convierte el fluido de trabajo de gas a líquido, de líquido a gas o de ambos, generando trabajo a partir de la expansión o compresión del fluido.

• Ciclo Rankine ( máquina de vapor clásica )
• Ciclo regenerativo ( máquina de vapor más eficiente que el ciclo Rankine )
• Ciclo orgánico de Rankine (Fase de cambio del refrigerante en rangos de temperatura de hielo y agua líquida caliente)
• Ciclo de vapor a líquido ( pájaro bebedero , inyector , rueda Minto )
• Ciclo de líquido a sólido ( levantamiento por congelación : el agua que cambia de hielo a líquido y viceversa puede levantar rocas hasta 60 cm).
• Ciclo de sólido a gas ( armas de fuego : los propulsores sólidos se queman y forman gases calientes).

En estos ciclos y motores el fluido de trabajo es siempre un gas (es decir, no hay cambio de fase):

• Ciclo de Carnot ( máquina térmica de Carnot )
• Ciclo de Ericsson (Barco Calórico John Ericsson)
• Ciclo Stirling ( motor Stirling , ^[12] dispositivos termoacústicos )
• Motor de combustión interna (MCI):
  • Ciclo Otto (por ejemplo , motor de gasolina )
  • Ciclo diésel (por ejemplo, motor diésel )
  • Ciclo Atkinson (motor Atkinson)
  • Ciclo Brayton o ciclo Joule originalmente ciclo Ericsson ( turbina de gas )
  • Ciclo Lenoir (por ejemplo, motor de chorro de pulso )
  • Ciclo Miller (motor Miller)

En estos ciclos y motores el fluido de trabajo es siempre como líquido:

• Ciclo Stirling ( motor Malone )

• Convertidor de energía termoeléctrica Johnson
• Termoeléctrica ( efecto Peltier-Seebeck )
• Celda termogalvánica
• Emisión termoiónica
• Refrigeración por termotúnel

• Motor termomagnético (Tesla)

Un refrigerador doméstico es un ejemplo de bomba de calor : un motor térmico en sentido inverso. Se utiliza trabajo para crear un diferencial de calor. Muchos ciclos pueden funcionar en sentido inverso para mover el calor del lado frío al lado caliente, haciendo que el lado frío sea más frío y el lado caliente más caliente. Las versiones de estos ciclos con motor de combustión interna no son, por su naturaleza, reversibles.

Los ciclos de refrigeración incluyen:

• Maquina de ciclo de aire
• Refrigerador de absorción de gas
• Refrigeración magnética
• Refrigerador criogénico Stirling
• Refrigeración por compresión de vapor
• Ciclo de Vuilleumier

El motor de evaporación Barton es un motor térmico basado en un ciclo que produce energía y aire húmedo enfriado a partir de la evaporación del agua en aire seco y caliente.

Los motores térmicos mesoscópicos son dispositivos a escala nanométrica que pueden servir para procesar flujos de calor y realizar trabajo útil a escalas pequeñas. Las aplicaciones potenciales incluyen, por ejemplo, dispositivos de refrigeración eléctricos. En estos motores térmicos mesoscópicos, el trabajo por ciclo de operación fluctúa debido al ruido térmico. Existe una igualdad exacta que relaciona el promedio de los exponentes del trabajo realizado por cualquier motor térmico y la transferencia de calor del baño térmico más caliente. ^[13] Esta relación transforma la desigualdad de Carnot en igualdad exacta. Esta relación también es una igualdad del ciclo de Carnot.

La eficiencia de un motor térmico relaciona la cantidad de trabajo útil que se produce para una cantidad determinada de energía térmica introducida.

De las leyes de la termodinámica , después de un ciclo completo: ^[14]

${\displaystyle W+Q=\Delta _{cycle}U=0}$

y por lo tanto

${\displaystyle W=-Q=-(Q_{c}+Q_{h})}$

dónde

${\displaystyle W=-\oint PdV}$es el trabajo neto extraído del motor en un ciclo. (Es negativo, en la convención IUPAC , ya que el trabajo lo realiza el motor).

${\displaystyle Q_{h}>0}$es la energía térmica extraída de la fuente de calor de alta temperatura en los alrededores en un ciclo. (Es positiva ya que se agrega energía térmica al motor).

${\displaystyle Q_{c}=-|Q_{c}|<0}$es el calor residual que emite el motor hacia el disipador de calor de temperatura fría. (Es negativo ^[14] ya que el motor pierde calor hacia el disipador).

En otras palabras, un motor térmico absorbe energía térmica de la fuente de calor de alta temperatura, convirtiendo parte de ella en trabajo útil y emitiendo el resto como calor residual al sumidero de calor de temperatura fría.

En general, la eficiencia de un proceso de transferencia de calor determinado se define por la relación entre "lo que se extrae" y "lo que se introduce". (En el caso de un refrigerador o una bomba de calor, que pueden considerarse como un motor térmico que funciona en sentido inverso, este es el coeficiente de rendimiento y es ≥ 1). En el caso de un motor, se desea extraer trabajo y se debe introducir calor , por ejemplo, a partir de la combustión de un combustible, por lo que la eficiencia del motor se define razonablemente como${\displaystyle Q_{h}}$

${\displaystyle \eta ={\frac {|W|}{Q_{h}}}={\frac {Q_{h}+Q_{c}}{Q_{h}}}=1+{\frac {Q_{c}}{Q_{h}}}=1-{\frac {|Q_{c}|}{Q_{h}}}}$

La eficiencia es inferior al 100% debido al calor residual que se pierde inevitablemente en el disipador frío (y el trabajo de compresión correspondiente que se realiza) durante la recompresión requerida a temperatura fría antes de que pueda ocurrir nuevamente la carrera de potencia del motor.${\displaystyle Q_{c}<0}$

La eficiencia máxima teórica de cualquier motor térmico depende únicamente de las temperaturas entre las que opera. Esta eficiencia se suele obtener utilizando un motor térmico ideal imaginario, como el motor térmico de Carnot , aunque otros motores que utilizan ciclos diferentes también pueden alcanzar la eficiencia máxima. Matemáticamente, después de un ciclo completo, el cambio total de entropía es cero:

${\displaystyle \ \ \ \Delta S_{h}+\Delta S_{c}=\Delta _{cycle}S=0}$

Nótese que es positivo porque la expansión isotérmica en la carrera de potencia aumenta la multiplicidad del fluido de trabajo mientras que es negativo porque la recompresión disminuye la multiplicidad. Si el motor es ideal y funciona de manera reversible , y , y por lo tanto ^{[15] [14]}${\displaystyle \Delta S_{h}}$${\displaystyle \Delta S_{c}}$${\displaystyle Q_{h}=T_{h}\Delta S_{h}}$${\displaystyle Q_{c}=T_{c}\Delta S_{c}}$

${\displaystyle Q_{h}/T_{h}+Q_{c}/T_{c}=0}$,

lo que da por tanto el límite de Carnot para la eficiencia del motor térmico,${\displaystyle Q_{c}/Q_{h}=-T_{c}/T_{h}}$

${\displaystyle \eta _{\text{max}}=1-{\frac {T_{c}}{T_{h}}}}$

donde es la temperatura absoluta de la fuente caliente y la del sumidero frío, normalmente medida en kelvins .${\displaystyle T_{h}}$${\displaystyle T_{c}}$

El razonamiento que sustenta esta máxima eficiencia es el siguiente. En primer lugar, se supone que, si es posible crear un motor térmico más eficiente que un motor de Carnot, se podría hacer funcionar en sentido inverso como una bomba de calor. Se puede utilizar un análisis matemático para demostrar que esta combinación supuesta daría como resultado una disminución neta de la entropía . Dado que, según la segunda ley de la termodinámica , esto es estadísticamente improbable hasta el punto de exclusión, la eficiencia de Carnot es un límite superior teórico para la eficiencia confiable de cualquier ciclo termodinámico.

Empíricamente, nunca se ha demostrado que un motor térmico funcione con mayor eficiencia que un motor térmico de ciclo de Carnot.

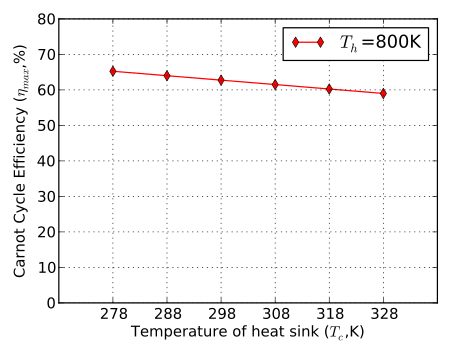
Las figuras 2 y 3 muestran variaciones en la eficiencia del ciclo de Carnot con la temperatura. La figura 2 indica cómo cambia la eficiencia con un aumento en la temperatura de adición de calor para una temperatura de entrada del compresor constante. La figura 3 indica cómo cambia la eficiencia con un aumento en la temperatura de rechazo de calor para una temperatura de entrada de la turbina constante.

Por su naturaleza, cualquier ciclo de Carnot de máxima eficiencia debe funcionar con un gradiente de temperatura infinitesimal ; esto se debe a que cualquier transferencia de calor entre dos cuerpos de diferentes temperaturas es irreversible, por lo que la expresión de eficiencia de Carnot se aplica solo al límite infinitesimal. El problema principal es que el objetivo de la mayoría de los motores térmicos es producir potencia, y rara vez se desea una potencia infinitesimal.

Una medida diferente de la eficiencia ideal de un motor térmico se da mediante consideraciones de termodinámica endorreversible , donde el sistema se divide en subsistemas reversibles, pero con interacciones no reversibles entre ellos. Un ejemplo clásico es el motor de Curzon-Ahlborn, ^[16] muy similar a un motor de Carnot, pero donde se permite que los depósitos térmicos a temperatura y sean diferentes de las temperaturas de la sustancia que pasa por el ciclo de Carnot reversible: y . Las transferencias de calor entre los depósitos y la sustancia se consideran conductivas (e irreversibles) en la forma . En este caso, se debe hacer un equilibrio entre la potencia de salida y la eficiencia. Si el motor funciona muy lentamente, el flujo de calor es bajo y se encuentra el resultado clásico de Carnot. ${\displaystyle T_{h}}$${\displaystyle T_{c}}$${\displaystyle T'_{h}}$${\displaystyle T'_{c}}$${\displaystyle dQ_{h,c}/dt=\alpha (T_{h,c}-T'_{h,c})}$${\displaystyle T\approx T'}$

${\displaystyle \eta =1-{\frac {T_{c}}{T_{h}}}}$,

Pero al precio de una potencia de salida que desaparece. Si, en cambio, se opta por hacer funcionar el motor a su máxima potencia de salida, la eficiencia se reduce.

${\displaystyle \eta =1-{\sqrt {\frac {T_{c}}{T_{h}}}}}$(Nota: T en unidades de K o °R )

Este modelo hace un mejor trabajo al predecir qué tan bien pueden funcionar los motores térmicos del mundo real (Callen 1985, ver también termodinámica endorreversible ):

Eficiencias de las centrales eléctricas ^[16]

Central eléctrica	${\displaystyle T_{c}}$(°C)	${\displaystyle T_{h}}$(°C)	${\displaystyle \eta }$(Carnot)	${\displaystyle \eta }$(Endorreversible)	${\displaystyle \eta }$(Observado)
Central eléctrica de carbón de West Thurrock (Reino Unido)	25	565	0,64	0,40	0,36
Central nuclear CANDU (Canadá)	25	300	0,48	0,28	0,30
Central geotérmica de Larderello (Italia)	80	250	0,33	0,178	0,16

Como se muestra, la eficiencia de Curzon-Ahlborn modela mucho más de cerca lo observado.

Los motores térmicos se conocen desde la antigüedad, pero recién en el siglo XVIII, durante la revolución industrial, se convirtieron en dispositivos útiles y hoy en día siguen desarrollándose.

Los ingenieros han estudiado los distintos ciclos de los motores térmicos para mejorar la cantidad de trabajo utilizable que pueden extraer de una fuente de energía determinada. El límite del ciclo de Carnot no se puede alcanzar con ningún ciclo basado en gas, pero los ingenieros han encontrado al menos dos formas de sortear ese límite y una forma de obtener una mayor eficiencia sin saltarse ninguna regla:

1. Aumentar la diferencia de temperatura en el motor térmico. La forma más sencilla de hacerlo es aumentar la temperatura del lado caliente, que es el enfoque utilizado en las turbinas de gas de ciclo combinado modernas . Desafortunadamente, los límites físicos (como el punto de fusión de los materiales utilizados para construir el motor) y las preocupaciones ambientales con respecto a la producción de NO _x (si la fuente de calor es la combustión con aire ambiente) restringen la temperatura máxima en los motores térmicos que funcionan. Las turbinas de gas modernas funcionan a temperaturas lo más altas posibles dentro del rango de temperaturas necesarias para mantener una salida de NO _{x aceptable} ^{[ cita requerida ]} . Otra forma de aumentar la eficiencia es reducir la temperatura de salida. Un nuevo método para hacerlo es usar fluidos de trabajo químicos mixtos y luego explotar el comportamiento cambiante de las mezclas. Uno de los más famosos es el llamado ciclo Kalina , que utiliza una mezcla 70/30 de amoníaco y agua como fluido de trabajo. Esta mezcla permite que el ciclo genere energía útil a temperaturas considerablemente más bajas que la mayoría de los otros procesos.
2. Explotar las propiedades físicas del fluido de trabajo. La explotación más común de este tipo es el uso de agua por encima del punto crítico ( agua supercrítica ). El comportamiento de los fluidos por encima de su punto crítico cambia radicalmente, y con materiales como el agua y el dióxido de carbono es posible explotar esos cambios de comportamiento para extraer una mayor eficiencia termodinámica del motor térmico, incluso si se utiliza un ciclo Brayton o Rankine bastante convencional. Un material más nuevo y muy prometedor para tales aplicaciones es el CO ₂ supercrítico . El SO ₂ y el xenón también se han considerado para tales aplicaciones. Las desventajas incluyen problemas de corrosión y erosión, el diferente comportamiento químico por encima y por debajo del punto crítico, las altas presiones necesarias y, en el caso del dióxido de azufre y, en menor medida, el dióxido de carbono, la toxicidad. Entre los compuestos mencionados, el xenón es el menos adecuado para su uso en un reactor nuclear debido a la alta sección transversal de absorción de neutrones de casi todos los isótopos del xenón , mientras que el dióxido de carbono y el agua también pueden funcionar como moderadores de neutrones para un reactor de espectro térmico.
3. Explotar las propiedades químicas del fluido de trabajo. Una explotación bastante nueva y novedosa es utilizar fluidos de trabajo exóticos con propiedades químicas ventajosas. Uno de ellos es el dióxido de nitrógeno (NO ₂ ), un componente tóxico del smog, que tiene un dímero natural como tetraóxido de dinitrógeno (N ₂ O ₄ ). A baja temperatura, el N ₂ O ₄ se comprime y luego se calienta. El aumento de temperatura hace que cada N ₂ O ₄ se rompa en dos moléculas de NO ₂ . Esto reduce el peso molecular del fluido de trabajo, lo que aumenta drásticamente la eficiencia del ciclo. Una vez que el NO ₂ se ha expandido a través de la turbina, se enfría por el disipador de calor , lo que hace que se recombine en N ₂ O ₄ . Luego, este es realimentado por el compresor para otro ciclo. Especies como el bromuro de aluminio (Al ₂ Br ₆ ), NOCl y Ga ₂ I ₆ se han investigado para tales usos. Hasta la fecha, sus inconvenientes no han justificado su uso, a pesar de las ganancias de eficiencia que se pueden lograr. ^[17]

Cada proceso es uno de los siguientes:

• isotérmico (a temperatura constante, mantenido con calor añadido o eliminado de una fuente o sumidero de calor)
• isobárico (a presión constante)
• isométrico/isocórico (a volumen constante), también denominado isovolumétrico
• adiabático (no se agrega ni se elimina calor del sistema durante el proceso adiabático)
• isentrópico (proceso adiabático reversible, no se agrega ni elimina calor durante el proceso isentrópico)

• Motor térmico de Carnot
• Cogeneración
• Refrigerador Einstein
• Bomba de calor
• Motor alternativo para una descripción general de la mecánica de los motores de pistón.
• Motor Stirling
• Termosíntesis
• Cronología de la tecnología de los motores térmicos

Wikimedia Commons alberga una categoría multimedia sobre Motores térmicos .

• Kroemer, Herbert; Kittel, Charles (1980). Física térmica (2.ª ed.). WH Freeman Company. ISBN 0-7167-1088-9.
• Callen, Herbert B. (1985). Termodinámica e introducción a la termoestadística (2.ª ed.). John Wiley & Sons, Inc. ISBN 0-471-86256-8.
• Robinson, Clark (1943). La termodinámica de las armas de fuego . MaGraw-Hill Book Company Inc.