16 celdas

Es posible que este artículo deba ser limpiado para cumplir con los estándares de calidad de Wikipedia . El problema específico es: eliminar las notas explicativas a pie de página. Los lectores de pantalla pueden colocarlas al final del artículo, lo que resulta confuso y fuera de contexto. Incorporarlas a la prosa principal o eliminarlas donde el contenido ya esté cubierto por un artículo vinculado. Por favor, ayude a mejorar este artículo si puede. ( Mayo de 2024 ) ( Aprenda cómo y cuándo eliminar este mensaje )

16 células (4-ortoplex)
Diagrama de Schlegel (vértices y aristas)
Tipo	Convexo regular 4-politopo 4- ortoplex 4- demicubo
Símbolo de Schläfli	{3,3,4}
Diagrama de Coxeter
Células	16 {3,3}
Caras	32 {3}
Bordes	24
Vértices	8
Figura de vértice	Octaedro
Polígono de Petrie	octágono
Grupo Coxeter	B 4 , [3,3,4], orden 384 D 4 , orden 192
Dual	Teseracto
Propiedades	politopo convexo , isogonal , isotoxal , isoédrico , regular , de Hanner
Índice uniforme	12

En geometría , el 16-cell es el 4-politopo convexo regular (análogo cuatridimensional de un sólido platónico) con símbolo de Schläfli {3,3,4}. Es uno de los seis 4-politopos convexos regulares descritos por primera vez por el matemático suizo Ludwig Schläfli a mediados del siglo XIX. ^[1] También se le llama C ₁₆ , hexadecacoron , ^[2] o hexdecaedroide [ sic ? ] . ^[3]

Es el miembro 4-dimensional de una familia infinita de politopos llamados politopos cruzados , ortoplexos o hiperoctaedros que son análogos al octaedro en tres dimensiones. Es el politopo de Coxeter. ^[4] El politopo dual es el teseracto ( cubo de 4 ), con el que se puede combinar para formar una figura compuesta . Las celdas del teseracto de 16 celdas son duales con respecto a los 16 vértices del teseracto.${\displaystyle \beta _{4}}$

La celda 16 es la segunda en la secuencia de 6 4-politopos regulares convexos (en orden de tamaño y complejidad). ^[a]

Cada uno de sus 4 politopos regulares convexos sucesores se puede construir como la envoltura convexa de un politopo compuesto de múltiples 16 celdas: el teseracto de 16 vértices como un compuesto de dos 16 celdas, el teseracto de 24 vértices y 24 celdas como un compuesto de tres 16 celdas, el teseracto de 120 vértices y 600 celdas como un compuesto de quince 16 celdas, y el teseracto de 120 vértices y 600 celdas como un compuesto de setenta y cinco 16 celdas. ^[b]

Politopos cuatripartitos convexos regulares
Grupo de simetría	Un 4	B4​		F4​	H4​
Nombre	5 celdas Hipertetraedro de 5 puntas	16 celdas Hiper - octaedro de 8 puntas	8 celdas Hipercubo de 16 puntos	24 celdas 24 puntos	600 celdas Hipericosaedro de 120 puntos	120 celdas Hiperdodecaedro de 600 puntos
Símbolo de Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Espejos Coxeter
Diédricos especulares	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
Gráfico
Vértices	5 tetraédricos	8 octaédrico	16 tetraédrico	24 cúbicos	120 icosaédricos	600 tetraédricos
Bordes	10 triangular	24 cuadrados	32 triangular	96 triangular	720 pentagonal	1200 triangular
Caras	10 triángulos	32 triángulos	24 cuadrados	96 triángulos	1200 triángulos	720 pentágonos
Células	5 tetraedros	16 tetraedros	8 cubos	24 octaedros	600 tetraedros	120 dodecaedros
Toros	1 5-tetraedro	2 8-tetraedro	2 4 cubos	4 6-octaedro	20 30-tetraedro	12 10-dodecaedro
Inscrito	120 en 120 celdas	675 en 120 celdas	2 de 16 celdas	3 de 8 celdas	25 24 celdas	10 600 celdas
Grandes polígonos		2 cuadrados x 3	4 rectángulos x 4	4 hexágonos x 4	12 decágonos x 6	100 hexágonos irregulares x 4
Polígonos de Petrie	1 pentágono x 2	1 octágono x 3	2 octágonos x 4	2 dodecágonos x 4	4 30-ágonos x 6	20 30-ágonos x 4
Radio largo	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$
Longitud del borde	${\displaystyle {\sqrt {\tfrac {5}{2}}}\aproximadamente 1,581}$	${\displaystyle {\sqrt {2}}\aproximadamente 1,414}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\displaystyle {\tfrac {1}{\phi }}\aproximadamente 0,618}$	${\displaystyle {\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\aproximadamente 0,270}$
Radio corto	${\displaystyle {\frac {1}{4}}}$	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\sqrt {\tfrac {1}{2}}}\aproximadamente 0,707}$	${\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\aproximadamente 0,926}$	${\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\aproximadamente 0,926}$
Área	${\displaystyle 10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\aproximadamente 10,825}$	${\displaystyle 32\left({\sqrt {\tfrac {3}{4}}}\right)\aproximadamente 27,713}$	${\estilo de visualización 24}$	${\displaystyle 96\left({\sqrt {\tfrac {3}{16}}}\right)\aproximadamente 41,569}$	${\displaystyle 1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\aproximadamente 198,48}$	${\displaystyle 720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\aproximadamente 90,366}$
Volumen	${\displaystyle 5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\aproximadamente 2,329}$	${\displaystyle 16\left({\tfrac {1}{3}}\right)\aproximadamente 5,333}$	${\estilo de visualización 8}$	${\displaystyle 24\left({\tfrac {\sqrt {2}}{3}}\right)\aproximadamente 11,314}$	${\displaystyle 600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\aproximadamente 16,693}$	${\displaystyle 120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\aproximadamente 18,118}$
4-Contenido	${\displaystyle {\tfrac {\sqrt {5}}{24}}\izquierda({\tfrac {\sqrt {5}}{2}}\derecha)^{4}\aproximadamente 0,146}$	${\displaystyle {\tfrac {2}{3}}\aproximadamente 0,667}$	${\estilo de visualización 1}$	${\estilo de visualización 2}$	${\displaystyle {\tfrac {{\text{Corto}}\times {\text{Vol}}}{4}}\aprox 3.863}$	${\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193}$

La celda 16 es el politopo cruzado de 4 dimensiones (4-ortoplex) , lo que significa que sus vértices se encuentran en pares opuestos en los 4 ejes de un sistema de coordenadas cartesianas (w, x, y, z).

Los ocho vértices son (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). Todos los vértices están conectados por aristas, excepto los pares opuestos. La longitud de la arista es √ 2 .

Las coordenadas de los vértices forman 6 cuadrados centrales ortogonales que se encuentran en los 6 planos de coordenadas. Los cuadrados en planos opuestos que no comparten un eje (por ejemplo, en los planos xy y wz ) son completamente disjuntos (no se intersecan en ningún vértice). ^[c]

Las 16 celdas constituyen una base ortonormal para la elección de un marco de referencia de 4 dimensiones, porque sus vértices definen exactamente los cuatro ejes ortogonales.

El símbolo de Schläfli del modelo de 16 celdas es {3,3,4}, lo que indica que sus celdas son tetraedros regulares {3,3} y su figura de vértice es un octaedro regular {3,4}. Hay 8 tetraedros, 12 triángulos y 6 aristas que se unen en cada vértice. Su figura de arista es un cuadrado. Hay 4 tetraedros y 4 triángulos que se unen en cada arista.

El sistema de 16 celdas está delimitado por 16 celdas , todas ellas tetraedros regulares . ^[e] Tiene 32 caras triangulares , 24 aristas y 8 vértices . Las 24 aristas delimitan 6 cuadrados centrales ortogonales que se encuentran en círculos máximos en los 6 planos de coordenadas (3 pares de cuadrados máximos completamente ortogonales ⁾ . En cada vértice, 3 cuadrados máximos se cruzan perpendicularmente. Las 6 aristas se encuentran en el vértice de la misma forma que las 6 aristas se encuentran en el vértice de una pirámide octaédrica canónica . ^[d] Los 6 planos centrales ortogonales del sistema de 16 celdas se pueden dividir en 4 hiperplanos centrales ortogonales (3-espacios), cada uno de los cuales forma un octaedro con 3 cuadrados máximos ortogonales.

Una proyección 3D de un sistema de 16 celdas que realiza una rotación simple

Una proyección 3D de 16 celdas realizando una doble rotación.

Las rotaciones en el espacio euclidiano de 4 dimensiones pueden verse como la composición de dos rotaciones bidimensionales en planos completamente ortogonales. ^[6] El sistema de 16 celdas es un marco simple en el que observar rotaciones de 4 dimensiones, porque cada uno de los 6 grandes cuadrados de las 16 celdas tiene otro gran cuadrado completamente ortogonal (hay 3 pares de cuadrados completamente ortogonales). [c] Muchas rotaciones de las 16 celdas pueden caracterizarse por el ángulo de rotación en uno de sus planos de grandes cuadrados (por ejemplo, el plano xy ) y otro ángulo de rotación en el plano de gran cuadrado completamente ortogonal (el plano wz ). ^{[j ]} Los grandes cuadrados completamente ortogonales tienen vértices disjuntos: 4 de los 8 vértices de las 16 celdas rotan en un plano y los otros 4 rotan independientemente en el plano completamente ortogonal. ^[g]

En 2 o 3 dimensiones, una rotación se caracteriza por un único plano de rotación; este tipo de rotación que tiene lugar en el espacio de 4 dimensiones se denomina rotación simple , en la que solo uno de los dos planos completamente ortogonales gira (el ángulo de rotación en el otro plano es 0). En el modelo de 16 celdas, una rotación simple en uno de los 6 planos ortogonales mueve solo 4 de los 8 vértices; los otros 4 permanecen fijos. (En la animación de rotación simple anterior, los 8 vértices se mueven porque el plano de rotación no es uno de los 6 planos de base ortogonales).

En una doble rotación, ambos conjuntos de 4 vértices se mueven, pero de forma independiente: los ángulos de rotación pueden ser diferentes en los 2 planos completamente ortogonales. Si los dos ángulos son iguales, se produce una rotación isoclínica de máxima simetría. ^[q] En la celda de 16, una rotación isoclínica de 90 grados de cualquier par de planos cuadrados completamente ortogonales lleva cada plano cuadrado a su plano cuadrado completamente ortogonal. ^[r]

Octaedro${\displaystyle \beta _{3}}$	16 celdas${\displaystyle \beta _{4}}$
Proyecciones ortogonales para inclinar el hiperplano hexagonal

La construcción más simple del sistema de 16 celdas se realiza sobre el politopo cruzado tridimensional, el octaedro . El octaedro tiene 3 ejes perpendiculares y 6 vértices en 3 pares opuestos (su polígono de Petrie es el hexágono ). Agregue otro par de vértices, sobre un cuarto eje perpendicular a los otros 3 ejes. Conecte cada nuevo vértice a los 6 vértices originales, agregando 12 nuevos bordes. Esto genera dos pirámides octaédricas sobre una base octaédrica compartida que se encuentra en el hiperplano central del sistema de 16 celdas. ^[10]

El octaedro con el que se inicia la construcción tiene tres cuadrados perpendiculares que se intersecan (que aparecen como rectángulos en las proyecciones hexagonales). Cada cuadrado se interseca con cada uno de los otros cuadrados en dos vértices opuestos, y dos de los cuadrados se cruzan en cada vértice. Luego se agregan dos puntos más en la cuarta dimensión (encima y debajo del hiperplano tridimensional). Estos nuevos vértices se conectan con todos los vértices del octaedro, lo que crea 12 nuevas aristas y tres cuadrados más (que aparecen de canto como los 3 diámetros del hexágono en la proyección) y tres octaedros más. ^[h]

También se ha creado algo sin precedentes. Nótese que cada cuadrado ya no se interseca con todos los demás cuadrados: sí se interseca con cuatro de ellos ( ahora tres de los cuadrados se cruzan en cada vértice), pero cada cuadrado tiene otro cuadrado con el que no comparte vértices: no está conectado directamente con ese cuadrado en absoluto. Estos dos cuadrados perpendiculares separados (hay tres pares de ellos) son como los bordes opuestos de un tetraedro : perpendiculares, pero no se intersecan. Se encuentran uno frente al otro (paralelos en cierto sentido), y no se tocan, pero también pasan uno a través del otro como dos eslabones perpendiculares de una cadena (pero a diferencia de los eslabones de una cadena tienen un centro común). Son un ejemplo de planos paralelos de Clifford , y el politopo regular de 16 celdas es el más simple en el que aparecen. El paralelismo de Clifford ^[l] de objetos de más de una dimensión (más que solo líneas curvas ) surge aquí y ocurre en todos los politopos regulares de 4 dimensiones posteriores, donde puede verse como la relación definitoria entre los 4-politopos regulares concéntricos disjuntos y sus partes correspondientes. Puede ocurrir entre politopos congruentes (similares) de 2 o más dimensiones. ^[11] Por ejemplo, como se señaló anteriormente, todos los 4-politopos regulares convexos posteriores son compuestos de múltiples 16 celdas; esas 16 celdas son politopos paralelos de Clifford .

El sistema de 16 celdas tiene dos construcciones de Wythoff a partir de tetraedros regulares, una forma regular y una forma alternada, que se muestran aquí como redes , la segunda representada por celdas tetraédricas de dos colores alternados. La forma alternada es una construcción de simetría inferior del sistema de 16 celdas llamada demitesseract .

La construcción de Wythoff replica la característica de 5 celdas del sistema de 16 celdas en un caleidoscopio de espejos. Cada politopo regular de 4 celdas tiene su ortosquema característico de 4 celdas, un sistema irregular de 5 celdas . ^[s] Hay tres politopos regulares de 4 celdas con celdas tetraédricas: el de 5 celdas , el de 16 celdas y el de 600 celdas . Aunque todos están limitados por celdas tetraédricas regulares , sus 5 celdas características (ortosquemas de 4 celdas) son pirámides tetraédricas diferentes , todas basadas en el mismo tetraedro irregular característico . Comparten el mismo tetraedro característico (ortosquema de 3 celdas) y el triángulo rectángulo característico (ortosquema de 2 celdas) porque tienen el mismo tipo de celda. ^[t]

Características de las 16 celdas [13]
	borde [14]	arco		diedro [15]
𝒍	${\displaystyle {\sqrt {2}}\approx 1.414}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$	120°	${\displaystyle {\tfrac {2\pi }{3}}}$
𝟀	${\displaystyle {\sqrt {\tfrac {2}{3}}}\approx 0.816}$	60″	${\displaystyle {\tfrac {\pi }{3}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
Yo [u]	${\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}$	45″	${\displaystyle {\tfrac {\pi }{4}}}$	45°	${\displaystyle {\tfrac {\pi }{4}}}$
𝟁	${\displaystyle {\sqrt {\tfrac {1}{6}}}\approx 0.408}$	30″	${\displaystyle {\tfrac {\pi }{6}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
${\displaystyle _{0}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {3}{4}}}\approx 0.866}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{1}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {1}{4}}}=0.5}$	45°	${\displaystyle {\tfrac {\pi }{4}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{2}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {1}{12}}}\approx 0.289}$	30°	${\displaystyle {\tfrac {\pi }{6}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{0}R^{4}/l}$	${\displaystyle 1}$
${\displaystyle _{1}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}$
${\displaystyle _{2}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{3}}}\approx 0.577}$
${\displaystyle _{3}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{4}}}=0.5}$

La característica de 5 celdas del sistema regular de 16 celdas está representada por el diagrama de Coxeter-Dynkin. , que puede leerse como una lista de los ángulos diedros entre sus facetas especulares. Es una pirámide tetraédrica irregular basada en el tetraedro característico del tetraedro regular . La pirámide regular de 16 celdas se subdivide por sus hiperplanos de simetría en 384 instancias de su característica pirámide de 5 celdas que se encuentran todas en su centro.

La celda característica de 5 (ortosquema de 4) tiene cuatro aristas más que su tetraedro característico de base (ortosquema de 3), uniendo los cuatro vértices de la base a su vértice (el quinto vértice del ortosquema de 4, en el centro de la celda regular de 16). ^[v] Si la celda regular de 16 tiene una arista de radio unidad y una longitud de arista 𝒍 = , las diez aristas de su celda característica de 5 tienen longitudes , , alrededor de su cara exterior de triángulo rectángulo (las aristas opuestas a los ángulos característicos 𝟀, 𝝉, 𝟁), ^[u] más , , (las otras tres aristas del ortosquema de 3 exteriores hacen faceta del tetraedro característico, que son los radios característicos del tetraedro regular), más , , , (aristas que son los radios característicos de la celda regular de 16). La ruta de 4 aristas a lo largo de las aristas ortogonales del ortoesquema es , , , , primero desde un vértice de 16 celdas hasta un centro de arista de 16 celdas, luego gira 90° hasta un centro de cara de 16 celdas, luego gira 90° hasta un centro de celda tetraédrica de 16 celdas, luego gira 90° hasta el centro de 16 celdas.${\displaystyle {\sqrt {2}}}$${\displaystyle {\sqrt {\tfrac {2}{3}}}}$${\displaystyle {\sqrt {\tfrac {1}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$${\displaystyle {\sqrt {\tfrac {3}{4}}}}$${\displaystyle {\sqrt {\tfrac {1}{4}}}}$${\displaystyle {\sqrt {\tfrac {1}{12}}}}$${\displaystyle 1}$${\displaystyle {\sqrt {\tfrac {1}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{3}}}}$${\displaystyle {\sqrt {\tfrac {1}{4}}}}$${\displaystyle {\sqrt {\tfrac {1}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$${\displaystyle {\sqrt {\tfrac {1}{4}}}}$${\displaystyle {\sqrt {\tfrac {1}{4}}}}$

Se puede construir un sistema de 16 celdas (de tres maneras diferentes) a partir de dos hélices de Boerdijk-Coxeter de ocho tetraedros encadenados, cada uno doblado en la cuarta dimensión en un anillo. ^{[16] [17]} Las dos hélices circulares se enroscan en espiral una alrededor de la otra, se anidan una dentro de la otra y pasan una a través de la otra formando un enlace de Hopf . Las 16 caras triangulares se pueden ver en una red 2D dentro de un mosaico triangular , con 6 triángulos alrededor de cada vértice. Los bordes morados representan el polígono de Petrie del sistema de 16 celdas. El anillo de ocho celdas de tetraedros contiene tres octagramas de diferentes colores, caminos circulares de ocho aristas que se enrollan dos veces alrededor del sistema de 16 celdas en cada tercer vértice del octagrama. Los bordes naranja y amarillo son dos mitades de cuatro aristas de un octagrama, que unen sus extremos para formar una banda de Möbius .

De este modo, la celda de 16 puede descomponerse en dos cadenas circulares de ocho tetraedros cada una, de cuatro aristas, separadas entre sí, una de ellas en espiral hacia la derecha (en el sentido de las agujas del reloj) y la otra hacia la izquierda (en el sentido contrario a las agujas del reloj). Los anillos celulares levógiros y diestros encajan entre sí, anidándose uno dentro del otro y llenando por completo la celda de 16, aunque tengan quiralidad opuesta. Esta descomposición puede verse en una construcción de duoantiprisma 4-4 de la celda de 16:o, Símbolo de Schläfli {2}⨂{2} o s{2}s{2}, simetría [4,2 ⁺ ,4], orden 64.

Tres caminos de ocho aristas (de diferentes colores) se mueven en espiral a lo largo de cada anillo de ocho celdas, formando ángulos de 90° en cada vértice. (En la hélice de Boerdijk-Coxeter antes de doblarse en un anillo, los ángulos en los diferentes caminos varían, pero no son de 90°). Tres caminos (con tres colores diferentes y ángulos aparentes) pasan por cada vértice. Cuando la hélice se dobla en un anillo, los segmentos de cada camino de ocho aristas (de varias longitudes) unen sus extremos, formando una banda de Möbius de ocho aristas de largo a lo largo de su circunferencia de un solo lado de 4𝝅, y una arista de ancho. ^[p] Las seis mitades de cuatro aristas de los tres caminos de ocho aristas forman cada una cuatro ángulos de 90°, pero no son los seis grandes cuadrados ortogonales: son cuadrados abiertos, hélices de 360° de cuatro aristas cuyos extremos abiertos son vértices antípodas . Los cuatro bordes provienen de cuatro grandes cuadrados diferentes y son mutuamente ortogonales. Combinados de extremo a extremo en pares de la misma quiralidad , los seis caminos de cuatro bordes forman tres bucles de Möbius de ocho bordes, octagramas helicoidales . Cada octagrama es a la vez un polígono de Petrie del sistema de 16 celdas y la pista helicoidal a lo largo de la cual los ocho vértices giran juntos, en una de las rotaciones isoclínicas distintivas del sistema de 16 celdas. ^[w]

Cinco maneras de mirar el mismo octagrama oblicuo [x]
Camino del borde	Polígono de Petrie [18]	16 celdas	Fibración discreta	Cuerdas de diámetro
Octagrama {8/3} [19]	Octagrama {8/1}	Avión Coxeter B4	Octagrama {8/2}=2{4}	Octagrama {8/4}=4{2}
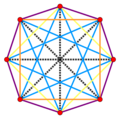Las ocho cuerdas √ 2 de la trayectoria del borde de una isoclina. [y]	Octágono oblicuo de ocho aristas de √ 2. El de 16 celdas tiene 3 de estos circuitos de 8 vértices.	Las 24 aristas √ 2 y los cuatro ejes ortogonales √ 4 .	Dos grandes cuadrados completamente ortogonales (disjuntos) de √ 2 aristas. [g]	Las cuatro cuerdas √ 4 de una isoclina. Cada cuarto vértice de la isoclina está unido a su vértice antípoda por un eje de 16 celdas. [y]

Cada hélice de ocho aristas es un octagrama oblicuo _{8/3} que da tres vueltas alrededor de la celda de 16 y visita cada vértice antes de cerrarse en un bucle. Sus ocho aristas de √ 2 son cuerdas de una isoclina , un arco helicoidal en el que los 8 vértices giran durante una rotación isoclínica. ^[p] Los ocho vértices de 16 celdas están separados por √ 2, excepto los vértices opuestos (antípodas), que están separados por √ 4. Un vértice que se mueve en la isoclina visita otros tres vértices que están separados por √ 2 antes de llegar al cuarto vértice que está separado por √ 4. ^[o]

El anillo de ocho celdas es quiral : hay una forma dextrógira que gira en el sentido de las agujas del reloj y una forma levógira que gira en el sentido contrario. El anillo de 16 celdas contiene una de cada una, por lo que también contiene una isoclina izquierda y otra derecha; la isoclina es el eje circular alrededor del cual gira el anillo de ocho celdas. Cada isoclina visita los ocho vértices del anillo de 16 celdas. ^[ab] Cada anillo de ocho celdas contiene la mitad de las 16 celdas, pero los 8 vértices; los dos anillos comparten los vértices, ya que se anidan entre sí y encajan entre sí. También comparten las 24 aristas, aunque las hélices de octagrama izquierda y derecha son caminos de ocho aristas diferentes. ^[ac]

Como hay tres pares de grandes cuadrados completamente ortogonales, ^[c] hay tres formas congruentes de componer un anillo de 16 celdas a partir de dos anillos de ocho celdas. El anillo de 16 celdas contiene tres pares de anillos de ocho celdas de izquierda a derecha en diferentes orientaciones, y cada anillo de celdas contiene su isoclina axial. ^[w] Cada par de isoclinas de izquierda a derecha es la trayectoria de un par de rotaciones isoclínicas de izquierda a derecha distintas: las rotaciones en un par de planos de rotación invariantes completamente ortogonales. ^[g] En cada vértice, hay tres grandes cuadrados y seis isoclinas de octagrama que se cruzan en el vértice y comparten una cuerda axial de 16 celdas. ^[ad]

Esta matriz de configuración representa las 16 celdas. Las filas y columnas corresponden a vértices, aristas, caras y celdas. Los números diagonales indican cuántos elementos de cada tipo hay en las 16 celdas. Los números no diagonales indican cuántos elementos de la columna hay en el elemento de la fila o en su interior.

${\displaystyle {\begin{bmatrix}{\begin{matrix}8&6&12&8\\2&24&4&4\\3&3&32&2\\4&6&4&16\end{matrix}}\end{bmatrix}}}$

Se puede teselar un espacio euclidiano de cuatro dimensiones mediante 16 celdas regulares. Esto se denomina panal de 16 celdas y tiene el símbolo de Schläfli {3,3,4,3}. Por lo tanto, la celda de 16 celdas tiene un ángulo diedro de 120°. ^[21] Cada celda de 16 tiene 16 vecinas con las que comparte un tetraedro, 24 vecinas con las que comparte solo una arista y 72 vecinas con las que comparte solo un punto. Veinticuatro celdas de 16 se encuentran en cualquier vértice dado en esta teselación.

La teselación dual, el panal de 24 celdas , {3,4,3,3}, está formada por 24 celdas regulares . Junto con el panal teseractico {4,3,3,4}, estas son las únicas tres teselaciones regulares de R ⁴ .

proyecciones ortográficas

Avión Coxeter	B4​	B3 / D4 / A2​	B2 / D3​
Gráfico
Simetría diedral	[8]	[6]	[4]
Avión Coxeter	F4​	Un 3
Gráfico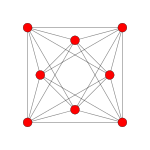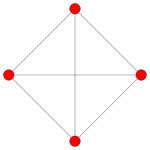
Simetría diedral	[12/3]	[4]

La proyección paralela de la primera celda del cubo de 16 celdas en el espacio tridimensional tiene una envoltura cúbica . Las celdas más cercanas y más lejanas se proyectan en tetraedros inscritos dentro del cubo, lo que corresponde a las dos formas posibles de inscribir un tetraedro regular en un cubo. Alrededor de cada uno de estos tetraedros hay otros 4 volúmenes tetraédricos (no regulares) que son las imágenes de las 4 celdas tetraédricas circundantes, llenando el espacio entre el tetraedro inscrito y el cubo. Las 6 celdas restantes se proyectan sobre las caras cuadradas del cubo. En esta proyección del cubo de 16 celdas, todas sus aristas se encuentran en las caras de la envoltura cúbica.

La proyección en perspectiva de celdas primero de las 16 celdas en el espacio de 3 tiene una envoltura triakistetraédrica . La disposición de las celdas dentro de esta envoltura es análoga a la de la proyección paralela de celdas primero.

La proyección paralela de primer vértice de la celda de 16 en el espacio de 3 tiene una envoltura octaédrica . Este octaedro se puede dividir en 8 volúmenes tetraédricos, cortando a lo largo de los planos de coordenadas. Cada uno de estos volúmenes es la imagen de un par de celdas en la celda de 16. El vértice más cercano de la celda de 16 al observador se proyecta sobre el centro del octaedro.

Finalmente, la proyección paralela con las aristas primero tiene una envoltura octaédrica acortada, y la proyección paralela con las caras primero tiene una envoltura bipiramidal hexagonal .

Una proyección tridimensional de las 16 celdas y las 4 esferas que se intersecan (un diagrama de Venn de 4 conjuntos) son topológicamente equivalentes.

El grupo de simetría de 16 celdas se denota B ₄ .

Existe una forma de simetría inferior del 16-cell , llamada demiteseracto o 4-demicube , un miembro de la familia de los semihipercubos , y representado por h{4,3,3} y diagramas de Coxeter. oSe puede dibujar bicolor con celdas tetraédricas alternas.

También se puede ver en forma de simetría inferior como un antiprisma tetraédrico , construido por 2 tetraedros paralelos en configuraciones duales, conectados por 8 tetraedros (posiblemente alargados). Se representa por s{2,4,3} y diagrama de Coxeter:.

También puede verse como un ortótopo snub 4 , representado por s{2 ^1,1,1 }, y diagrama de Coxeter:o.

Con el teseracto construido como un duoprisma 4-4 , las 16 celdas pueden verse como su dual, una duopirámide 4-4 .

Nombre	Diagrama de Coxeter	Símbolo de Schläfli	Notación de Coxeter	Orden	Figura de vértice
Regular de 16 celdas		{3,3,4}	[3,3,4]	384
Demitesseract Quasiregular de 16 células	= =	h{4,3,3} {3,3 1,1 }	[3 1,1,1 ] = [1 + ,4,3,3]	192
Duoprisma alternado 4-4		2s{4,2,4}	[[4,2 + ,4]]	64
Antiprisma tetraédrico		s{2,4,3}	[2 + ,4,3]	48
Prisma cuadrado alterno		sr{2,2,4}	[(2,2) + ,4]	16
Desaire 4- ortotopo	=	s{2 1,1,1 }	[2,2,2] + = [2 1,1,1 ] +	8
4- fusil
		{3,3,4}	[3,3,4]	384
		{4}+{4} o 2{4}	[[4,2,4]] = [8,2 + ,8]	128
		{3,4}+{ }	[4,3,2]	96
		{4}+2{ }	[4,2,2]	32
		{ }+{ }+{ }+{ } o 4{ }	[2,2,2]	16

El polígono de Möbius-Kantor es un polígono complejo regular ₃ {3} ₃ ,, comparte los mismos vértices que la celda 16. Tiene 8 vértices y 8 aristas de 3 lados. ^{[22] [23]}${\displaystyle \mathbb {C} ^{2}}$

El polígono complejo regular, ₂ {4} ₄ ,, tiene una representación real como una celda de 16 en un espacio de 4 dimensiones con 8 vértices, 16 aristas de 2 caras, solo la mitad de las aristas de la celda de 16. Su simetría es ₄ [4] ₂ , orden 32. ^[24]${\displaystyle \mathbb {C} ^{2}}$

Proyecciones ortográficas de polígonos de ₂ {4} ₄

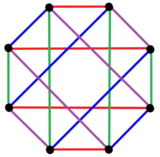En el plano de Coxeter B 4 , 2 {4} 4 tiene 8 vértices y 16 aristas 2, que se muestran aquí con 4 conjuntos de colores.

Los 8 vértices están agrupados en 2 conjuntos (mostrados en rojo y azul), cada uno conectado únicamente con aristas a los vértices del otro conjunto, lo que hace de este polígono un gráfico bipartito completo , K 4,4 . [25]

El teseracto y el 16-cell regular son los miembros regulares de un conjunto de 15 4-politopos uniformes con la misma simetría B ₄ . El 16-cell es también uno de los politopos uniformes de simetría D ₄ .

El de 16 celdas también está relacionado con el panal cúbico , el panal dodecaédrico de orden 4 y el panal hexagonal de orden 4 , que tienen figuras de vértice octaédricas .

Pertenece a la secuencia de 4-politopos {3,3,p} que tienen celdas tetraédricas. La secuencia incluye tres 4-politopos regulares del 4-espacio euclidiano, el {3,3,3} de 5 celdas , el {3,3,4} de 16 celdas y el {3,3,5} de 600 celdas ), y el panal tetraédrico de orden 6 {3,3,6} del espacio hiperbólico.

Es el primero de una secuencia de politopos y panales cuasirregulares h{4,p,q}, y una secuencia de semisimetría para formas regulares {p,3,4}.

• 24 celdas
• 4-politopo
• Politopo D4

• Weisstein, Eric W. "16 celdas". MathWorld .
• Der 16-Zeller (16 celdas) Politopos regulares de Marco Möller en R ⁴ (alemán)
• Descripción y diagramas de proyecciones de 16 celdas
• Klitzing, Richard. "Polítopos uniformes 4D (policora) x3o3o4o – hex".