Figura de isotoxal

En geometría , un politopo (por ejemplo, un polígono o un poliedro ) o un mosaico es isotoxal (del griego τόξον  'arco') o transitivo en sus aristas si sus simetrías actúan transitivamente sobre sus aristas . De manera informal, esto significa que solo hay un tipo de arista para el objeto: dadas dos aristas, hay una traslación , rotación y/o reflexión que moverá una arista hacia la otra mientras deja la región ocupada por el objeto sin cambios.

Un polígono isotoxal es un polígono de lados pares, es decir, equilátero , pero no todos los polígonos equiláteros son isotoxales. Los duales de los polígonos isotoxales son polígonos isogonales . Los isotoxales -gonos son simétricos centralmente , por lo que también son zonógonos .${\estilo de visualización 4n}$

En general, un -gono isotoxal (no regular) tiene simetría diedro . Por ejemplo, un rombo (no cuadrado) es un " × -gono" isotoxal (cuadrilátero) con simetría. Todos los -gonos regulares (también con impar ) son isotoxales, con el doble del orden de simetría mínimo: un -gono regular tiene simetría diedro.${\estilo de visualización 2n}$${\displaystyle \mathrm {D} _{n},(^{*}nn)}$ ${\estilo de visualización 2}$${\estilo de visualización 2}$${\displaystyle \mathrm {D} _{2},(^{*}22)}$${\displaystyle {\color {azul real}n}}$${\estilo de visualización n}$${\estilo de visualización n}$${\displaystyle \mathrm {D} _{n},(^{*}nn)}$

Un isotoxal -gono con ángulo interno externo se puede denotar por El ángulo interno interno puede ser menor o mayor que , formando polígonos convexos o cóncavos respectivamente.${\displaystyle {\mathbf {2}}n}$${\estilo de visualización \alpha}$${\displaystyle \{n_{\alpha }\}.}$${\estilo de visualización (\beta )}$${\estilo de visualización 180}$${\displaystyle {\color {azul real}^{\mathsf {o}}},}$

Un estrella -gono${\displaystyle {\color {azul real}{\mathbf {2}}n}}$ también puede ser isotoxal, denotado por con y con el máximo común divisor donde es el número de giro o densidad . ^[1] Los vértices internos cóncavos se pueden definir para Si entonces se "reduce" a un compuesto de copias rotadas de${\displaystyle \{(n/q)_{\alpha }\},}$${\displaystyle q\leq n-1}$ ${\displaystyle \mcd(n,q)=1,}$${\estilo de visualización q}$${\displaystyle q<n/2.}$${\displaystyle D=\mcd(n,q)\geq 2,}$${\displaystyle \{(n/q)_{\alpha }\}=\{(Dm/Dp)_{\alpha }\}}$${\displaystyle D\{(m/p)_{\alpha }\}}$${\estilo de visualización D}$${\displaystyle \{(m/p)_{\alpha }\}.}$

Precaución:

Los vértices de no siempre se colocan como los de mientras que los vértices del regular se colocan como los del regular${\displaystyle \{(n/q)_{\alpha }\}}$${\displaystyle \{n_{\alpha}\},}$${\displaystyle \{n/q\}}$${\displaystyle \{n\}.}$

Se puede definir un conjunto de teselas "uniformes" , en realidad teselas isogonales que utilizan polígonos isotoxales como caras menos simétricas que las regulares.

Ejemplos de polígonos y compuestos isotoxales no regulares

Número de lados:${\estilo de visualización 2n}$	2×2 (simb. cent.)	2×3	2×4 (simb. cent.)	2×5	2×6 (simb. cent.)	2×7	2×8 (simb. cent.)
${\displaystyle \{n_{\alpha}\}}$ Convexo: Cóncavo: ${\displaystyle \beta <180^{\circ }.}$ ${\displaystyle \beta >180^{\circ }.}$	${\displaystyle \{2_{\alpha}\}}$	${\displaystyle \{3_{\alpha}\}}$	${\displaystyle \{4_{\alpha}\}}$	${\displaystyle \{5_{\alpha}\}}$	${\displaystyle \{6_{\alpha}\}}$	${\displaystyle \{7_{\alpha}\}}$	${\displaystyle \{8_{\alpha}\}}$
2 vueltas 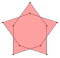${\displaystyle \{(n/2)_{\alpha }\}}$	--	${\displaystyle \{(3/2)_{\alpha}\}}$	${\displaystyle 2\{2_{\alpha}\}}$	${\displaystyle \{(5/2)_{\alpha}\}}$	${\displaystyle 2\{3_{\alpha}\}}$	${\displaystyle \{(7/2)_{\alpha}\}}$	${\displaystyle 2\{4_{\alpha}\}}$
3 vueltas ${\displaystyle \{(n/3)_{\alpha }\}}$	--	--	${\displaystyle \{(4/3)_{\alpha}\}}$	${\displaystyle \{(5/3)_{\alpha}\}}$	${\displaystyle 3\{2_{\alpha}\}}$	${\displaystyle \{(7/3)_{\alpha }\}}$	${\displaystyle \{(8/3)_{\alpha }\}}$
4 vueltas ${\displaystyle \{(n/4)_{\alpha }\}}$	--	--	--	${\displaystyle \{(5/4)_{\alpha}\}}$	${\displaystyle 2\{(3/2)_{\alpha}\}}$	${\displaystyle \{(7/4)_{\alpha }\}}$	${\displaystyle 4\{2_{\alpha}\}}$
5 vueltas ${\displaystyle \{(n/5)_{\alpha }\}}$	--	--	--	--	${\displaystyle \{(6/5)_{\alpha }\}}$	${\displaystyle \{(7/5)_{\alpha}\}}$	${\displaystyle \{(8/5)_{\alpha }\}}$
6 vueltas ${\displaystyle \{(n/6)_{\alpha }\}}$	--	--	--	--	--	${\displaystyle \{(7/6)_{\alpha}\}}$	${\displaystyle 2\{(4/3)_{\alpha}\}}$
7 vueltas ${\displaystyle \{(n/7)_{\alpha }\}}$	--	--	--	--	--	--	${\displaystyle \{(8/7)_{\alpha}\}}$

Los poliedros regulares son isoédricos (transitivos por caras), isogonales (transitivos por vértices) e isotoxales (transitivos por aristas).

Los poliedros cuasirregulares , como el cuboctaedro y el icosidodecaedro , son isogonales e isotoxales, pero no isoédricos. Sus duales, incluidos el dodecaedro rómbico y el triacontaedro rómbico , son isoédricos e isotoxales, pero no isogonales.

Ejemplos

Poliedro cuasirregular	Poliedro dual cuasirregular	Poliedro estrellado cuasirregular	Poliedro de estrella dual cuasirregular	Teselación cuasirregular	Teselación dual cuasirregular
Un cuboctaedro es un poliedro isogonal e isotoxal.	Un dodecaedro rómbico es un poliedro isoédrico e isotoxal.	Un gran icosidodecaedro es un poliedro estrellado isogonal e isotoxal.	Un gran triacontaedro rómbico es un poliedro estrellado isoédrico e isotoxal.	El mosaico trihexagonal es un mosaico isogonal e isotoxal.	El mosaico de rombos es un mosaico isoédrico e isotoxal con simetría p6m (*632).

No todos los poliedros o teselaciones bidimensionales construidas a partir de polígonos regulares son isotoxales. Por ejemplo, el icosaedro truncado (el conocido balón de fútbol) no es isotoxal, ya que tiene dos tipos de aristas: hexágono-hexágono y hexágono-pentágono, y no es posible que una simetría del sólido mueva una arista hexágono-hexágono sobre una arista hexágono-pentágono.

Un poliedro isotoxal tiene el mismo ángulo diedro para todos los bordes.

El dual de un poliedro convexo es también un poliedro convexo. ^[2]

El dual de un poliedro no convexo es también un poliedro no convexo. ^[2] (Por contraposición.)

El dual de un poliedro isotoxal es también un poliedro isotoxal. (Véase el artículo Poliedro dual ).

Hay nueve poliedros isotoxales convexos : los cinco sólidos platónicos ( regulares ) , los dos núcleos comunes ( cuasirregulares ) de los sólidos platónicos duales y sus dos duales.

Hay catorce poliedros isotoxales no convexos: los cuatro poliedros de Kepler-Poinsot (regulares) , los dos núcleos comunes (cuasirregulares) de los poliedros duales de Kepler-Poinsot y sus dos duales, más los tres poliedros estelares ditrigonales cuasirregulares (3 | pq ) y sus tres duales.

Hay al menos cinco compuestos poliédricos isotoxales: los cinco compuestos poliédricos regulares ; sus cinco duales son también los cinco compuestos poliédricos regulares (o un gemelo quiral).

Hay al menos cinco teselaciones poligonales isotoxales del plano euclidiano, e infinitas teselaciones poligonales isotoxales del plano hiperbólico, incluidas las construcciones de Wythoff a partir de las teselaciones hiperbólicas regulares { p , q }, y grupos no rectos ( pqr ).

• Tabla de ángulos diedros de poliedros
• Vértice-transitivo
• Transición facial
• Célula transitiva

• Peter R. Cromwell, Polyhedra , Cambridge University Press, 1997, ISBN 0-521-55432-2 , Transitividad, pág. 371 
• Grünbaum, Branko ; Shephard, GC (1987). Mosaicos y patrones . Nueva York: WH Freeman. ISBN 0-7167-1193-1.(6.4 Tejas isotoxales, págs. 309–321)
• Coxeter, Harold Scott MacDonald ; Longuet-Higgins, MS; Miller, JCP (1954), "Poliedros uniformes", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences , 246 (916): 401–450, Bibcode :1954RSPTA.246..401C, doi :10.1098/rsta.1954.0003, ISSN  0080-4614, JSTOR  91532, MR  0062446, S2CID  202575183