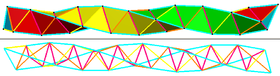
Hélice de Boerdijk-Coxeter

Hélices de Coxeter a partir de tetraedros regulares

Giro en sentido antihorario y horario

Los bordes se pueden colorear en 6 grupos, 3 hélices principales (cian), con los bordes cóncavos formando una hélice lenta hacia adelante (magenta) y dos hélices hacia atrás (amarillo y naranja) [1]

La hélice de Boerdijk-Coxeter , llamada así por HSM Coxeter y Arie Hendrick Boerdijk  [es] , es un apilamiento lineal de tetraedros regulares , dispuestos de modo que las aristas del complejo que pertenecen a un solo tetraedro formen tres hélices entrelazadas . Hay dos formas quirales , con devanados en el sentido de las agujas del reloj o en el sentido contrario. A diferencia de cualquier otro apilamiento de sólidos platónicos , la hélice de Boerdijk-Coxeter no es rotacionalmente repetitiva en el espacio tridimensional. Incluso en una cadena infinita de tetraedros apilados, no habrá dos tetraedros con la misma orientación, porque el paso helicoidal por celda no es una fracción racional del círculo. Sin embargo, se han encontrado formas modificadas de esta hélice que son rotacionalmente repetitivas, ^[2] y en el espacio de 4 dimensiones esta hélice se repite en anillos de exactamente 30 celdas tetraédricas que teselan la superficie de 3 esferas de la de 600 celdas , una de las seis policoras convexas regulares .

Buckminster Fuller lo denominó tetrahélice y lo consideró con elementos tetraédricos regulares e irregulares. ^[3]

Las coordenadas de los vértices de la hélice de Boerdijk-Coxeter compuesta por tetraedros con longitud de arista unitaria se pueden escribir en la forma

${\displaystyle (r\cos n\theta ,r\sin n\theta ,nh)}$

donde , , y es un entero arbitrario. Los dos valores diferentes de corresponden a dos formas quirales. Todos los vértices están ubicados en el cilindro con radio a lo largo del eje z. Dado cómo se alternan los tetraedros, esto da un giro aparente de cada dos tetraedros. Hay otro cilindro inscrito con radio dentro de la hélice. ^[4]${\displaystyle r=3{\sqrt {3}}/10}$${\displaystyle \theta =\pm \cos ^{-1}(-2/3)\aproximadamente 131,81^{\circ }}$${\displaystyle h=1/{\sqrt {10}}}$${\estilo de visualización n}$${\estilo de visualización \theta}$${\estilo de visualización r}$${\displaystyle 2\theta -{\frac {4}{3}}\pi \aproximadamente 23,62^{\circ }}$${\displaystyle 3{\sqrt {2}}/20}$

Las 600 celdas se dividen en 20 anillos de 30 tetraedros , cada uno una hélice de Boerdijk-Coxeter. ^[5] Cuando se superpone a la curvatura de 3 esferas se vuelve periódica, con un período de diez vértices, que abarca las 30 celdas. El colectivo de tales hélices en las 600 celdas representa una fibración de Hopf discreta . ^{[6] Mientras que en 3 dimensiones las aristas son hélices, en la} topología de 3 esferas impuesta son geodésicas y no tienen torsión . Se enroscan una alrededor de la otra de forma natural debido a la fibración de Hopf. ^[7] El colectivo de aristas forma otra fibración de Hopf discreta de 12 anillos con 10 vértices cada uno. Estos corresponden a anillos de 10 dodecaedros en las 120 celdas duales .

Además, la partición de 16 celdas en dos anillos de 8 tetraedros , con cuatro aristas de largo, y la partición de 5 celdas en un único anillo degenerado de 5 tetraedros .

4-politopo	Anillos	Tetraedros/anillos	Duración de los ciclos	Neto	Proyección
600 celdas	20	30	30, 10 3 , 15 2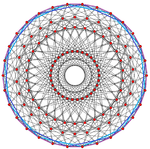
16 celdas	2	8	8, 8, 4 2
5 celdas	1	5	(5, 5), 5

Las pirámides cuadradas equiláteras también se pueden encadenar entre sí formando una hélice, con dos configuraciones de vértice , 3.4.3.4 y 3.3.4.3.3.4. Esta hélice existe como un anillo finito de 30 pirámides en un politopo de 4 dimensiones .

Y las pirámides pentagonales equiláteras se pueden encadenar con 3 configuraciones de vértice, 3.3.5, 3.5.3.5 y 3.3.3.5.3.3.5:

La Torre de Arte Mito se basa en una hélice de Boerdijk-Coxeter.

• Anillos de células paralelas de Clifford
• Poliedro toroidal
• Grupo de líneas#Simetría helicoidal
• Apeirogon sesgado # Apeirogons helicoidales en 3 dimensiones

• Animación de la hélice de Boerdijk-Coxeter
• Datos de la tetrahélice