Hiperrectángulo
Ortotopo hiperrectángulo | |
|---|---|
 Un cuboide rectangular es un 3-ortotopo | |
| Tipo | Prisma |
| Caras | 2 n |
| Bordes | n ×2n − 1 |
| Vértices | 2 n |
| Símbolo de Schläfli | {}×{}×···×{} = {} n [1] |
| Diagrama de Coxeter |    ··· ··· |
| Grupo de simetría | [2 n −1 ] , orden 2 n |
| Poliedro dual | Fusil rectangular n |
| Propiedades | convexo , zonoedro , isogonal |

En geometría , un hiperrectángulo (también llamado caja , hipercaja , -celda u ortótopo [2] ), es la generalización de un rectángulo (una figura plana ) y del cuboide rectangular (una figura sólida ) a dimensiones superiores . Una condición necesaria y suficiente es que sea congruente con el producto cartesiano de intervalos finitos . [3] Esto significa que un sólido rectangular -dimensional tiene cada una de sus aristas igual a uno de los intervalos cerrados utilizados en la definición. Toda -celda es compacta . [4] [5]
Si todas las aristas tienen la misma longitud, se trata de un hipercubo . Un hiperrectángulo es un caso especial de paraleletopo .
Definición formal
Para cada entero de a , sean y números reales tales que . El conjunto de todos los puntos en cuyas coordenadas satisfacen las desigualdades es una -celda . [6]
Intuición
Una celda de dimensión α es especialmente simple. Por ejemplo, una celda 1 es simplemente el intervalo con α . Una celda 2 es el rectángulo formado por el producto cartesiano de dos intervalos cerrados, y una celda 3 es un sólido rectangular.
Los lados y los bordes de una celda no necesitan ser iguales en longitud (euclidiana); aunque el cubo unitario (que tiene límites de igual longitud euclidiana) es una celda de 3, el conjunto de todas las celdas de 3 con bordes de igual longitud es un subconjunto estricto del conjunto de todas las celdas de 3.
Tipos
Un ortotopo de cuatro dimensiones es probablemente un hipercuboide. [7]
El caso especial de un ortótopo n -dimensional donde todos los bordes tienen la misma longitud es el n - cubo o hipercubo. [2]
Por analogía, el término "hiperrectángulo" puede referirse a productos cartesianos de intervalos ortogonales de otros tipos, como rangos de claves en la teoría de bases de datos o rangos de números enteros , en lugar de números reales . [8]
Politopo dual
| n -fusil | |
|---|---|
 Ejemplo: 3 fusiles | |
| Tipo | Prisma |
| Caras | 2 n |
| Vértices | 2 n |
| Símbolo de Schläfli | {}+{}+···+{} = n {} [1] |
| Diagrama de Coxeter |     ... ...  |
| Grupo de simetría | [2 n −1 ] , orden 2 n |
| Poliedro dual | n -ortotopo |
| Propiedades | convexo , isotópico |
El politopo dual de un n -ortótopo se ha denominado de diversas formas: n - ortoplex rectangular , n - fusil rómbico o n - rombo . Está formado por 2 n puntos ubicados en el centro de las caras rectangulares del ortótopo.
El símbolo Schläfli de un fusil n se puede representar mediante una suma de n segmentos de línea ortogonales: { } + { } + ... + { } o n { }.
Un 1-fusil es un segmento de línea . Un 2-fusil es un rombo . Sus selecciones transversales planas en todos los pares de ejes son rombos .
| norte | Imagen de ejemplo |
|---|---|
| 1 |  Segmento de línea { }  |
| 2 | 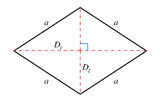 Rombo { } + { } = 2{ }    |
| 3 | 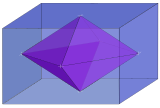 3-ortoplex rómbico dentro de 3-ortotopo { } + { } + { } = 3{ }      |
Véase también
Notas
- ^ ab NW Johnson : Geometrías y transformaciones , (2018) ISBN 978-1-107-10340-5 Capítulo 11: Grupos de simetría finitos , 11.5 Grupos esféricos de Coxeter, pág. 251
- ^Por Coxeter, 1973
- ^ Foran (1991)
- ^ Rudin (1976:39)
- ^ Foran (1991:24)
- ^ Rudin (1976:31)
- ^ Hirotsu, Takashi (2022). "Hipercuboides de tamaño normal en un hipercubo dado". arXiv : 2211.15342 .
- ^ Véase, por ejemplo, Zhang, Yi; Munagala, Kamesh; Yang, Jun (2011), "Almacenamiento de matrices en disco: teoría y práctica revisadas" (PDF) , Proc. VLDB , 4 (11): 1075–1086, doi :10.14778/3402707.3402743.
Referencias
- Coxeter, Harold Scott MacDonald (1973). Politopos regulares (3.ª ed.). Nueva York: Dover. pp. 122-123. ISBN 0-486-61480-8.
Enlaces externos
- Weisstein, Eric W. "Ortótopo". MathWorld .
- Foran, James (7 de enero de 1991). Fundamentos del análisis real. CRC Press. ISBN 9780824784539. Recuperado el 23 de mayo de 2014 .
- Rudin, Walter (1976). Principios del análisis matemático . McGraw-Hill.












![{\estilo de visualización [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
