Ángulo diedro

| Tipos de ángulos |
|---|
| Ángulos 2D |
| Esférico |
| Pares de ángulos 2D |
Complementario |
| Ángulos 3D |
Diédrico |
Un ángulo diedro es el ángulo entre dos planos o semiplanos que se intersecan . En química , es el ángulo en el sentido de las agujas del reloj entre semiplanos que pasan por dos conjuntos de tres átomos , que tienen dos átomos en común. En geometría de sólidos , se define como la unión de una línea y dos semiplanos que tienen esta línea como borde común . En dimensiones superiores , un ángulo diedro representa el ángulo entre dos hiperplanos . Se dice que los planos de una máquina voladora están en un ángulo diedro positivo cuando tanto el plano principal de estribor como el de babor (comúnmente llamados "alas") están inclinados hacia arriba con respecto al eje lateral; cuando están inclinados hacia abajo, se dice que están en un ángulo diedro negativo.
Antecedentes matemáticos
Cuando los dos planos que se intersectan se describen en términos de coordenadas cartesianas mediante las dos ecuaciones
El ángulo diedro entre ellos viene dado por:
y satisface Se puede observar fácilmente que el ángulo es independiente de y .
Alternativamente, si n A y n B son vectores normales a los planos, se tiene
donde n A · n B es el producto escalar de los vectores y | n A | | n B | es el producto de sus longitudes. [1]
El valor absoluto es necesario en las fórmulas anteriores, ya que los planos no se modifican al cambiar todos los signos de los coeficientes en una ecuación o al reemplazar un vector normal por su opuesto.
Sin embargo, los valores absolutos pueden y deben evitarse cuando se considera el ángulo diedro de dos semiplanos cuyos límites son la misma línea. En este caso, los semiplanos pueden describirse mediante un punto P de su intersección y tres vectores b 0 , b 1 y b 2 tales que P + b 0 , P + b 1 y P + b 2 pertenecen respectivamente a la línea de intersección, al primer semiplano y al segundo semiplano. El ángulo diedro de estos dos semiplanos se define mediante
- ,
y satisface En este caso, cambiar los dos semiplanos da el mismo resultado, y lo mismo ocurre con reemplazar con En química (ver más abajo), definimos un ángulo diedro tal que reemplazar con cambia el signo del ángulo, que puede estar entre − π y π .
En física de polímeros
En algunas áreas científicas como la física de polímeros , se puede considerar una cadena de puntos y enlaces entre puntos consecutivos. Si los puntos están numerados secuencialmente y ubicados en las posiciones r 1 , r 2 , r 3 , etc. entonces los vectores de enlace se definen por u 1 = r 2 − r 1 , u 2 = r 3 − r 2 y u i = r i+1 − r i , de manera más general. [2] Este es el caso de las cadenas cinemáticas o aminoácidos en una estructura de proteína . En estos casos, a menudo uno está interesado en los semiplanos definidos por tres puntos consecutivos y el ángulo diedro entre dos de esos semiplanos consecutivos. Si u 1 , u 2 y u 3 son tres vectores de enlace consecutivos, la intersección de los semiplanos está orientada, lo que permite definir un ángulo diedro que pertenece al intervalo (− π , π ] . Este ángulo diedro está definido por [3]
o, utilizando la función atan2 ,
Este ángulo diedro no depende de la orientación de la cadena (orden en el que se consideran los puntos); invertir este orden consiste en reemplazar cada vector por su vector opuesto e intercambiar los índices 1 y 3. Ambas operaciones no cambian el coseno, pero sí el signo del seno. Por lo tanto, juntas, no cambian el ángulo.
Una fórmula más simple para el mismo ángulo diedro es la siguiente (la prueba se da a continuación)
o equivalentemente,
Esto se puede deducir de las fórmulas anteriores utilizando la fórmula del producto cuadruple vectorial y el hecho de que un producto triple escalar es cero si contiene dos veces el mismo vector:
Dada la definición del producto vectorial , esto significa que es el ángulo en el sentido de las agujas del reloj del cuarto átomo en comparación con el primer átomo, mientras se mira hacia abajo el eje desde el segundo átomo hasta el tercero. Los casos especiales (se podría decir los casos habituales) son , y , que se denominan conformaciones trans , gauche + y gauche − .
En estereoquímica
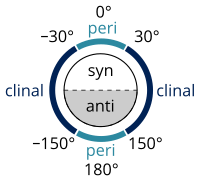 | 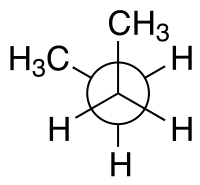 |  |
| Nombres de configuración según el ángulo diedro | syn n- Butano en la conformación gauche − (−60°) Proyección de Newman | syn n- Proyección de caballete de butano |

En estereoquímica , un ángulo de torsión se define como un ejemplo particular de un ángulo diedro, que describe la relación geométrica de dos partes de una molécula unidas por un enlace químico . [4] [5] Cada conjunto de tres átomos no colineales de una molécula define un semiplano. Como se explicó anteriormente, cuando dos de estos semiplanos se intersecan (es decir, un conjunto de cuatro átomos enlazados consecutivamente), el ángulo entre ellos es un ángulo diedro. Los ángulos diedros se utilizan para especificar la conformación molecular . [6] Las disposiciones estereoquímicas correspondientes a ángulos entre 0° y ±90° se denominan syn (s), las correspondientes a ángulos entre ±90° y 180° anti (a). De manera similar, las disposiciones correspondientes a ángulos entre 30° y 150° o entre −30° y −150° se denominan clinales (c) y aquellas entre 0° y ±30° o ±150° y 180° se denominan periplanares (p).
Los dos tipos de términos pueden combinarse para definir cuatro rangos de ángulos: 0° a ±30° sinperiplanar (sp); 30° a 90° y −30° a −90° sinclinal (sc); 90° a 150° y −90° a −150° anticlinal (ac); ±150° a 180° antiperiplanar (ap). La conformación sinperiplanar también se conoce como conformación syn o cis ; la antiperiplanar como anti o trans ; y la sinclinal como gauche o skew .
Por ejemplo, con n - butano se pueden especificar dos planos en términos de los dos átomos de carbono centrales y cualquiera de los átomos de carbono del metilo. La conformación syn mostrada arriba, con un ángulo diedro de 60° es menos estable que la conformación anti con un ángulo diedro de 180°.
Para el uso macromolecular se recomiendan los símbolos T, C, G + , G − , A + y A − (ap, sp, +sc, −sc, +ac y −ac respectivamente).
Proteínas

Un diagrama de Ramachandran (también conocido como diagrama de Ramachandran o diagrama [ φ , ψ ]), desarrollado originalmente en 1963 por GN Ramachandran , C. Ramakrishnan y V. Sasisekharan, [7] es una forma de visualizar las regiones energéticamente permitidas para los ángulos diedros de la cadena principal ψ contra φ de los residuos de aminoácidos en la estructura de la proteína . En una cadena de proteínas se definen tres ángulos diedros:
- ω (omega) es el ángulo en la cadena C α − C' − N − C α ,
- φ (phi) es el ángulo en la cadena C' − N − C α − C'
- ψ (psi) es el ángulo en la cadena N − C α − C' − N (llamado φ′ por Ramachandran)
La figura de la derecha ilustra la ubicación de cada uno de estos ángulos (pero no muestra correctamente la forma en que están definidos). [8]
La planaridad del enlace peptídico generalmente restringe el ω a 180° (el caso trans típico ) o 0° (el caso cis poco frecuente). La distancia entre los átomos de C α en los isómeros trans y cis es de aproximadamente 3,8 y 2,9 Å, respectivamente. La gran mayoría de los enlaces peptídicos en las proteínas son trans , aunque el enlace peptídico al nitrógeno de la prolina tiene una mayor prevalencia de cis en comparación con otros pares de aminoácidos. [9]
Los ángulos diedros de la cadena lateral se designan con χ n (chi- n ). [10] Tienden a agruparse cerca de 180°, 60° y −60°, que se denominan conformaciones trans , gauche − y gauche + . La estabilidad de ciertos ángulos diedros de la cadena lateral se ve afectada por los valores φ y ψ . [11] Por ejemplo, existen interacciones estéricas directas entre el C γ de la cadena lateral en el rotámero gauche + y el nitrógeno de la cadena principal del siguiente residuo cuando ψ está cerca de -60°. [12] Esto es evidente a partir de distribuciones estadísticas en bibliotecas de rotámeros dependientes de la cadena principal .
Geometría
Cada poliedro tiene un ángulo diedro en cada arista que describe la relación de las dos caras que comparten esa arista. Este ángulo diedro, también llamado ángulo de la cara , se mide como el ángulo interno con respecto al poliedro. Un ángulo de 0° significa que los vectores normales de las caras son antiparalelos y las caras se superponen entre sí, lo que implica que es parte de un poliedro degenerado . Un ángulo de 180° significa que las caras son paralelas, como en un mosaico . Un ángulo mayor de 180° existe en porciones cóncavas de un poliedro.
Todos los ángulos diedros de un poliedro transitivo de aristas tienen el mismo valor. Esto incluye los 5 sólidos platónicos , los 13 sólidos Catalan , los 4 poliedros de Kepler-Poinsot , los dos sólidos cuasirregulares y los dos sólidos duales cuasirregulares.
Ley de los cosenos para el ángulo diedro
Dadas 3 caras de un poliedro que se encuentran en un vértice común P y tienen aristas AP, BP y CP, el coseno del ángulo diedro entre las caras que contienen a APC y BPC es: [13]
Esto se puede deducir de la ley esférica de los cosenos .
Véase también
Referencias
- ^ "Ángulo entre dos planos". TutorVista.com . Archivado desde el original el 28 de octubre de 2020. Consultado el 6 de julio de 2018 .
- ^ Kröger, Martin (2005). Modelos para líquidos poliméricos y anisotrópicos . Springer. ISBN 3540262105.
- ^ Blondel, Arnaud; Karplus, Martin (7 de diciembre de 1998). "Nueva formulación para derivadas de ángulos de torsión y ángulos de torsión impropios en mecánica molecular: eliminación de singularidades". Journal of Computational Chemistry . 17 (9): 1132–1141. doi :10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T.
- ^ IUPAC , Compendio de terminología química , 2.ª edición (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "Ángulo de torsión". doi :10.1351/goldbook.T06406
- ^ IUPAC , Compendio de terminología química , 2.ª edición (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "Ángulo diedro". doi :10.1351/goldbook.D01730
- ^ Anslyn, Eric; Dennis Dougherty (2006). Química orgánica física moderna . University Science. pág. 95. ISBN 978-1891389313.
- ^ Ramachandran, GN; Ramakrishnan, C.; Sasisekharan, V. (1963). "Estereoquímica de las configuraciones de la cadena polipeptídica". Revista de Biología Molecular . 7 : 95–9. doi :10.1016/S0022-2836(63)80023-6. PMID 13990617.
- ^ Richardson, JS (1981). "La anatomía y taxonomía de la estructura de las proteínas". Anatomía y taxonomía de las estructuras de las proteínas . Avances en la química de las proteínas. Vol. 34. págs. 167–339. doi :10.1016/S0065-3233(08)60520-3. ISBN 9780120342341.PMID 7020376 .
- ^ Singh J, Hanson J, Heffernan R, Paliwal K, Yang Y, Zhou Y (agosto de 2018). "Detección de isómeros cis de prolina y no prolina en estructuras de proteínas a partir de secuencias mediante aprendizaje profundo de conjuntos residuales". Journal of Chemical Information and Modeling . 58 (9): 2033–2042. doi :10.1021/acs.jcim.8b00442. PMID 30118602. S2CID 52031431.
- ^ "Conformación de la cadena lateral".
- ^ Dunbrack, RL Jr.; Karplus, M (20 de marzo de 1993). "Biblioteca de rotámeros dependiente de la cadena principal para proteínas. Aplicación a la predicción de la cadena lateral". Journal of Molecular Biology . 230 (2): 543–74. doi :10.1006/jmbi.1993.1170. PMID 8464064.
- ^ Dunbrack, RL Jr; Karplus, M (mayo de 1994). "Análisis conformacional de las preferencias de rotámeros dependientes de la estructura principal de las cadenas laterales de proteínas". Nature Structural Biology . 1 (5): 334–40. doi :10.1038/nsb0594-334. PMID 7664040. S2CID 9157373.
- ^ "calculadora del ángulo diedro de un poliedro" www.had2know.com . Archivado desde el original el 25 de noviembre de 2015 . Consultado el 25 de octubre de 2015 .
Enlaces externos
- El ángulo diedro en la carpintería en Tips.FM
- El análisis de los cinco poliedros regulares proporciona una derivación paso a paso de estos valores exactos.

















![{\displaystyle (\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3})=[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{1}]\mathbf {u} _{2}-[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{2}]\mathbf {u} _{1}=[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{1}]\mathbf {u} _{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78dfd079ef2f25bdd1f87bcbd9d208c2af4ca75b)



