Grafo bipartito completo

Grafo bipartito completo
Un gráfico bipartito completo con m = 5 y n = 3
Vértices	n + m
Bordes	Minnesota
Radio	${\displaystyle \left\{{\begin{array}{ll}1&m=1\vee n=1\\2&{\text{de lo contrario}}\end{array}}\right.}$
Diámetro	${\displaystyle \left\{{\begin{array}{ll}1&m=n=1\\2&{\text{de lo contrario}}\end{array}}\right.}$
Circunferencia	${\displaystyle \left\{{\begin{array}{ll}\infty &m=1\lor n=1\\4&{\text{de lo contrario}}\end{array}}\right.}$
Automorfismos	${\displaystyle \left\{{\begin{array}{ll}2m!n!&n=m\\m!n!&{\text{de lo contrario}}\end{array}}\right.}$
Número cromático	2
Índice cromático	máx{ m , n }
Espectro	${\displaystyle \left\{0^{n+m-2},(\pm {\sqrt {nm}})^{1}\right\}}$
Notación	K { m , n }
Tabla de gráficos y parámetros

En el campo matemático de la teoría de grafos , un grafo bipartito completo o biclique es un tipo especial de grafo bipartito donde cada vértice del primer conjunto está conectado a cada vértice del segundo conjunto. ^{[1] [2]}

La teoría de grafos se suele fechar como algo que comienza con el trabajo de Leonhard Euler de 1736 sobre los Siete Puentes de Königsberg . Sin embargo, los dibujos de grafos bipartitos completos ya se imprimieron en 1669, en relación con una edición de las obras de Ramon Llull editada por Athanasius Kircher . ^{[3] [4]} El propio Llull había hecho dibujos similares de grafos completos tres siglos antes. ^[3]

Un grafo bipartito completo es un grafo cuyos vértices pueden ser particionados en dos subconjuntos V ₁ y V ₂ tales que ninguna arista tiene ambos puntos finales en el mismo subconjunto, y cada arista posible que podría conectar vértices en diferentes subconjuntos es parte del grafo. Es decir, es un grafo bipartito ( V ₁ , V ₂ , E ) tal que para cada dos vértices v ₁ ∈ V ₁ y v ₂ ∈ V ₂ , v ₁ v ₂ es una arista en E . Un grafo bipartito completo con particiones de tamaño | V ₁ | = m y | V ₂ | = n , se denota K _{m , n} ; ^{[1] [2]} cada dos grafos con la misma notación son isomorfos .

• Para cualquier k , K _{1, k} se llama estrella . ^[2] Todos los gráficos bipartitos completos que son árboles son estrellas.
  • El gráfico K _1,3 se denomina garra y se utiliza para definir los gráficos sin garra . ^[5]
• El gráfico K _3,3 se denomina gráfico de utilidades . Este uso proviene de un problema matemático estándar en el que tres servicios públicos deben estar conectados a tres edificios; es imposible resolverlo sin cruces debido a la falta de planaridad de K _3,3 . ^[6]
• Los biclíneos máximos que se encuentran como subgrafos del dígrafo de una relación se denominan conceptos . Cuando se forma un retículo tomando encuentros y uniones de estos subgrafos, la relación tiene un retículo de conceptos inducido . Este tipo de análisis de relaciones se denomina análisis formal de conceptos .

Ejemplo K _{p , p} grafos bipartitos completos ^[7]

K3,3​	K 4,4	K5,5​
3 colores de borde	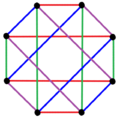4 colores de borde	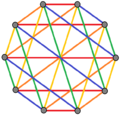5 coloraciones de borde
Los polígonos regulares complejos de la forma 2{4} p tienen gráficos bipartitos completos con 2 p vértices (rojo y azul) y p 2 2-aristas. También se pueden dibujar con p coloraciones de aristas.

• Dado un gráfico bipartito, probar si contiene un subgráfico bipartito completo K _{i , i} para un parámetro  i es un problema NP-completo . ^[8]
• Un grafo plano no puede contener K _3,3 como menor ; un grafo exterior-planar no puede contener K _3,2 como menor (Estas no son condiciones suficientes para la planaridad y exterior-planaridad, pero son necesarias). Por el contrario, todo grafo no plano contiene K _3,3 o el grafo completo K ₅ como menor; este es el teorema de Wagner . ^[9]
• Todo grafo bipartito completo. K _{n , n} es un grafo de Moore y una jaula ( n ,4) . ^[10]
• Los grafos bipartitos completos K _{n , n} y K _{n , n +1} tienen el máximo número posible de aristas entre todos los grafos libres de triángulos con el mismo número de vértices; este es el teorema de Mantel . El resultado de Mantel se generalizó a grafos k -partitos y grafos que evitan camarillas más grandes como subgrafos en el teorema de Turán , y estos dos grafos bipartitos completos son ejemplos de grafos de Turán , los grafos extremales para este problema más general. ^[11]
• El gráfico bipartito completo K _{m , n} tiene un número de cobertura de vértices de min { m , n } y un número de cobertura de aristas de max { m , n }.
• El gráfico bipartito completo K _{m , n} tiene un conjunto independiente máximo de tamaño max { m , n }.
• La matriz de adyacencia de un grafo bipartito completo K _{m , n} tiene valores propios √ nm , − √ nm y 0; con multiplicidad 1, 1 y n + m − 2 respectivamente. ^[12]
• La matriz laplaciana de un grafo bipartito completo K _{m , n} tiene valores propios n + m , n , m y 0; con multiplicidad 1, m − 1 , n − 1 y 1 respectivamente.
• Un gráfico bipartito completo K _{m , n} tiene m ^{n −1} n ^{m −1} árboles de expansión . ^[13]
• Un gráfico bipartito completo K _{m , n} tiene una coincidencia máxima de tamaño min { m , n }.
• Un gráfico bipartito completo K _{n , n} tiene una coloración de arista n adecuada correspondiente a un cuadrado latino . ^[14]
• Todo grafo bipartito completo es un grafo modular : cada triple de vértices tiene una mediana que pertenece a los caminos más cortos entre cada par de vértices. ^[15]

• Gráfico libre de bicliques , una clase de gráficos dispersos definidos por la evitación de subgrafos bipartitos completos
• Gráfico de corona , un gráfico formado al eliminar una coincidencia perfecta de un gráfico bipartito completo
• Gráfico multipartito completo , una generalización de gráficos bipartitos completos a más de dos conjuntos de vértices
• Ataque biclicuo