5-símplex

5-politopo regular

Hexaterón 5-símplex (hix)
Tipo	5-politopo uniforme
Símbolo de Schläfli	{3 ⁴ }
Diagrama de Coxeter
4 caras	6	6 {3,3,3}
Células	15	15 {3,3}
Caras	20	20 {3}
Bordes	15
Vértices	6
Figura de vértice	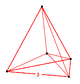5 celdas
Grupo Coxeter	A ₅ , [3 ⁴ ], orden 720
Dual	auto-dual
Punto base	(0,0,0,0,0,1)
Circunradio	0,645497
Propiedades	convexo , isogonal regular , autodual

En geometría de cinco dimensiones , un 5- símplex es un 5-politopo regular autodual . Tiene seis vértices , 15 aristas , 20 caras triangulares, 15 celdas tetraédricas y 6 facetas de 5 celdas . Tiene un ángulo diedro de cos ⁻¹ ( ⁠ 1/5) , o aproximadamente 78,46°.

El 5-símplex es una solución al problema: hacer 20 triángulos equiláteros usando 15 fósforos, donde cada lado de cada triángulo es exactamente un fósforo.

Nombres alternativos

También se le puede llamar hexaterón o hexa-5-topo , ya que es un politopo de 6 facetas en 5 dimensiones. El nombre hexaterón se deriva de hexa- , que significa que tiene seis facetas , y teron ( ter- es una corrupción de tetra- ), que significa que tiene facetas de cuatro dimensiones.

Jonathan Bowers le da al hexaterón el acrónimo hix . ^[1]

Como configuración

Esta matriz de configuración representa el 5-símplex. Las filas y columnas corresponden a vértices, aristas, caras, celdas y 4-caras. Los números diagonales indican cuántos elementos de cada uno hay en todo el 5-símplex. Los números no diagonales indican cuántos elementos de la columna hay en el elemento de la fila o en él. La matriz de este símplex autodual es idéntica a su rotación de 180 grados. ^[2]^[3]

${\begin{bmatrix}{\begin{matrix}6&5&10&10&5\\2&15&4&6&4\\3&3&20&3&3\\4&6&4&15&2\\5&10&10&5&6\end{matrix}}\end{bmatrix}}$

Coordenadas cartesianas del hexaterón regular

El hexaterón se puede construir a partir de un triángulo de 5 celdas agregando un sexto vértice tal que sea equidistante de todos los demás vértices del triángulo de 5 celdas.

Las coordenadas cartesianas de los vértices de un hexaterón regular centrado en el origen que tiene una longitud de arista de 2 son:

{\begin{aligned}&\left({\frac {1}{\sqrt {15}}},\ {\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)\\[5pt]&\left({\frac {1}{\sqrt {15}}},\ {\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ -{\frac {2}{\sqrt {3}}},\ 0\right)\\[5pt]&\left({\frac {1}{\sqrt {15}}},\ {\frac {1}{\sqrt {10}}},\ -{\frac {\sqrt {3}}{\sqrt {2}}},\ 0,\ ​​0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ -{\tfrac {2{\sqrt {2}}}{\sqrt {5}}},\ 0,\ ​​0,\ ​​0\right)\\[5pt]&\left(-{\tfrac {\sqrt {5}}{\sqrt {3}}},\ 0,\ ​​0,\ ​​0,\ ​​0\right)\end{aligned}}

Los vértices del 5-símplex se pueden posicionar de forma más sencilla en un hiperplano en el 6-espacio como permutaciones de (0,0,0,0,0,1) o (0,1,1,1,1,1). Estas construcciones se pueden considerar como facetas del 6-ortoplex o del 6-cubo rectificado respectivamente.

Imágenes proyectadas

proyecciones ortográficas
Un _avión de Coxeter	Un ₅	Un ₄
Gráfico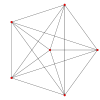
Simetría diedral	[6]	[5]
Un _avión de Coxeter	Un ₃	Un ₂
Gráfico
Simetría diedral	[4]	[3]

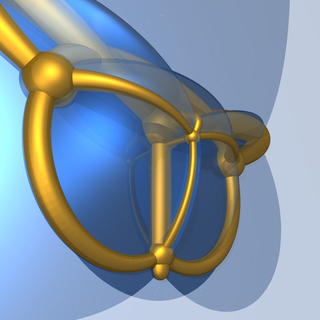Proyección estereográfica 4D a 3D del diagrama de Schlegel 5D a 4D del hexaterón.

Formas de simetría inferior

Una forma de simetría inferior es una pirámide de 5 celdas {3,3,3}∨( ), con un orden de simetría [3,3,3] de 120, construida como una base de 5 celdas en un hiperplano de 4 espacios y un punto de vértice por encima del hiperplano. Los cinco lados de la pirámide están formados por celdas de 5 celdas. Estas se ven como figuras de vértice de 6-politopos regulares truncados , como un 6-cubo truncado .

Otra forma es {3,3}∨{ }, con orden de simetría [3,3,2,1] 48, la unión de un diágono ortogonal y un tetraedro, desplazados ortogonalmente, con todos los pares de vértices conectados entre sí. Otra forma es {3}∨{3}, con orden de simetría [3,2,3,1] 36, y simetría extendida [[3,2,3],1], orden 72. Representa la unión de 2 triángulos ortogonales, desplazados ortogonalmente, con todos los pares de vértices conectados entre sí.

La forma { }∨{ }∨{ } tiene simetría [2,2,1,1], orden 8, extendida permutando 3 segmentos como [3[2,2],1] o [4,3,1,1], orden 48.

Estos se ven en las figuras de vértice de politopos regulares de 6 bits truncados y tritruncados, como un cubo de 6 bits truncados y un simplex de 6 bits truncados . Las etiquetas de borde aquí representan los tipos de caras a lo largo de esa dirección y, por lo tanto, representan diferentes longitudes de borde.

La figura del vértice del panal 5-símplex omnitruncado ,, es un 5-símplex con un ciclo de polígono de Petrie de 5 aristas largas. Su simetría es isomorfa al grupo diedro Dih ₆ o grupo de rotación simple [6,2] ⁺ , orden 12.

Figuras de vértice para 6-politopos uniformes
Unirse	{3,3,3}∨( )	{3,3}∨{ }	{3}∨{3}	{ }∨{ }∨{ }
Simetría	[3,3,3,1] Orden 120	[3,3,2,1] Orden 48	[[3,2,3],1] Orden 72	[3[2,2],1,1]=[4,3,1,1] Orden 48	~[6] o ~[6,2] ⁺ Orden 12
Diagrama
Politopo	6-símplex truncado	bitruncado 6-símplex	tritruncado 6-símplex	Prisma 3-3-3	Panal de abeja 5-símplex omnitruncado

Compuesto

El compuesto de dos 5-símplex en configuraciones duales se puede ver en esta proyección del plano de Coxeter A6 , con vértices y aristas de 5-símplex rojo y azul. Este compuesto tiene simetría [[3,3,3,3]], orden 1440. La intersección de estos dos 5-símplex es un 5-símplex birectificado uniforme .=∩.

5-politopos uniformes relacionados

Es el primero de una serie dimensional de politopos y panales uniformes, expresados por Coxeter como la serie 1 _3k . Existe un caso degenerado de 4 dimensiones como teselación de 3 esferas, un hosoedro tetraédrico .

1 figuras dimensionales _{de 3k}
Espacio	Finito				Euclidiano	Hiperbólico
norte	4	5	6	7	8	9
Grupo Coxeter	Un ₃ Un ₁	Un ₅	D6	E7	${\tilde {E}}_{7}$ =E ₇⁺	${\bar {T}}_{8}$ = _E7⁺⁺
Diagrama de Coxeter
Simetría	[3 ^−1,3,1 ]	[3 ^0,3,1 ]	[3 ^1,3,1 ]	[3 ^2,3,1 ]	[[3 ^3,3,1 ]]	[3 ^4,3,1 ]
Orden	48	720	23.040	2.903.040	∞
Gráfico					-	-
Nombre	1 _3,-1	130	1 ₃₁	1 ₃₂	1 ₃₃	134

Es el primero de una serie dimensional de politopos y panales uniformes, expresados por Coxeter como series 3 _k1 . Existe un caso degenerado de 4 dimensiones como teselación de 3 esferas, un diedro tetraédrico .

Figuras tridimensionales de 3 _k1
Espacio	Finito				Euclidiano	Hiperbólico
norte	4	5	6	7	8	9
Grupo Coxeter	Un ₃ Un ₁	Un ₅	D6	E7	${\tilde {E}}_{7}$ =E ₇⁺	${\bar {T}}_{8}$ = _E7⁺⁺
Diagrama de Coxeter
Simetría	[3 ^−1,3,1 ]	[3 ^0,3,1 ]	[[3 ^1,3,1 ]] = [4,3,3,3,3]	[3 ^2,3,1 ]	[3 ^3,3,1 ]	[3 ^4,3,1 ]
Orden	48	720	46.080	2.903.040	∞
Gráfico					-	-
Nombre	3 _1,-1	310	3 ₁₁	3 ₂₁	3 ₃₁	341

El 5-símplex, como politopo 2 _20, es el primero en la serie dimensional 2 _2k .

2 _2k figuras de n dimensiones
Espacio	Finito			Euclidiano	Hiperbólico
norte	4	5	6	7	8
Grupo Coxeter	Un ₂ Un ₂	Un ₅	E6	${\tilde {E}}_{6}$ =E ₆⁺	E6 ₊₊
Diagrama de Coxeter
Gráfico				∞	∞
Nombre	2 _2,-1	220	2 ₂₁	2 ₂₂	223

El 5-símplex regular es uno de los 19 polígonos uniformes basados en el grupo de Coxeter [3,3,3,3] , todos mostrados aquí en proyecciones ortográficas del plano de Coxeter A _5. (Los vértices están coloreados por orden de superposición de proyecciones, rojo, naranja, amarillo, verde, cian, azul, violeta tienen progresivamente más vértices)

Politopos A5
Para	el ₁	dos	t0,1	t0,2	1,2	t0,3
1,3	0,4	0,1,2	t0,1,3	0,2,3	1,2,3	0,1,4
0,2,4	0,1,2,3	0,1,2,4	0,1,3,4	0,1,2,3,4

Véase también

11 celdas

Notas

^ Klitzing, Richard. "Polítopos uniformes 5D (politera) x3o3o3o3o — hix".
^ Coxeter 1973, §1.8 Configuraciones
^ Coxeter, HSM (1991). Politopos complejos regulares (2.ª ed.). Cambridge University Press. pág. 117. ISBN 9780521394901.

Referencias

Gosset, T. (1900). "Sobre las figuras regulares y semirregulares en el espacio de n dimensiones". Messenger of Mathematics. Macmillan. págs. 43–44.
Coxeter, HSM :
- — (1973). "Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)". Politopos regulares (3.ª ed.). Dover. pp. 296. ISBN 0-486-61480-8.
- Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Caleidoscopios: escritos selectos de HSM Coxeter. Wiley. ISBN 978-0-471-01003-6.
  - (Artículo 22) — (1940). "Polítopos regulares y semirregulares I". Math. Zeit . 46 : 380–407. doi :10.1007/BF01181449. S2CID 186237114.
  - (Artículo 23) — (1985). "Polítopos regulares y semirregulares II". Math. Zeit . 188 (4): 559–591. doi :10.1007/BF01161657. S2CID 120429557.
  - (Artículo 24) — (1988). "Polítopos regulares y semirregulares III". Math. Zeit . 200 : 3–45. doi :10.1007/BF01161745. S2CID 186237142.
Conway, John H .; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "26. Hemicubos: 1 _n1 ". Las simetrías de las cosas . pág. 409. ISBN 978-1-56881-220-5.
Johnson, Norman (1991). "Polítopos uniformes" (manuscrito). Norman Johnson.
- Johnson, NW (1966). La teoría de politopos uniformes y panales (PhD). Universidad de Toronto.

Enlaces externos

Olshevsky, George. "Simplex". Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
Politopos de varias dimensiones, Jonathan Bowers
Glosario multidimensional

en a mi Politopos fundamentales convexos regulares y uniformes en dimensiones 2–10
Familia	Un	Bn	Yo ₂ (p) / D _n	Mi ₆ / Mi ₇ / Mi ₈ / Fa ₄ / Sol ₂	H- _n
Polígono regular	Triángulo	Cuadrado	p-gon	Hexágono	Pentágono
Poliedro uniforme	Tetraedro	Octaedro • Cubo	Semicubo		Dodecaedro • Icosaedro
Policoron uniforme	Pentachoron	16 celdas • Tesseract	Acto de Demitesseract	24 celdas	120 celdas • 600 celdas
Politopo 5 uniforme	5-símplex	5-ortoplex • 5-cubo	5-demicubes
Politopo uniforme de 6 elementos	6-símplex	6-ortoplex • 6-cubo	6-demicubes	1 ₂₂ • 2 ₂₁
Politopo 7 uniforme	7-símplex	7-ortoplex • 7-cubo	7-demicube	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Politopo 8 uniforme	8-símplex	8-ortoplex • 8-cubo	8-demicubes	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Politopo uniforme de 9 elementos	9-símplex	9-ortoplex • 9-cubo	9-demicubes
Politopo uniforme de 10	10-símplex	10-ortoplex • 10-cubo	10-demicubes
Politopo uniforme n	n - símplex	n - ortoplex • n - cubo	n - demicubo	1 _k2 • 2 _k1 • k21	n - politopo pentagonal
Temas: Familias de politopos • Politopo regular • Lista de politopos regulares y compuestos

[1] Klitzing, Richard. "Polítopos uniformes 5D (politera) x3o3o3o3o — hix".

[2] Coxeter 1973, §1.8 Configuraciones

[3] Coxeter, HSM (1991). Politopos complejos regulares (2.ª ed.). Cambridge University Press. pág. 117. ISBN 9780521394901.