Espacio de ocho dimensiones

En matemáticas , una sucesión de n números reales puede entenderse como una posición en un espacio de n dimensiones . Cuando n = 8, el conjunto de todas esas posiciones se denomina espacio de 8 dimensiones . A menudo, estos espacios se estudian como espacios vectoriales , sin ninguna noción de distancia. El espacio euclidiano de ocho dimensiones es un espacio de ocho dimensiones dotado de la métrica euclidiana .

En términos más generales, el término puede referirse a un espacio vectorial de ocho dimensiones sobre cualquier cuerpo , como un espacio vectorial complejo de ocho dimensiones , que tiene 16 dimensiones reales. También puede referirse a una variedad de ocho dimensiones, como una 8-esfera , o a una variedad de otras construcciones geométricas.

Un politopo en ocho dimensiones se llama 8-politopo. Los más estudiados son los politopos regulares , de los cuales sólo hay tres en ocho dimensiones : el 8-símplex , el 8-cubo y el 8-ortoplex . Una familia más amplia son los 8-politopos uniformes , construidos a partir de dominios de simetría fundamental de reflexión, cada dominio definido por un grupo de Coxeter . Cada politopo uniforme está definido por un diagrama de Coxeter-Dynkin anillado . El 8-demicubo es un politopo único de la familia D ₈ , y 4 ₂₁ , 2 ₄₁ y 1 ₄₂ politopos de la familia E ₈ .

Politopos regulares y uniformes en ocho dimensiones
(mostrados como proyecciones ortogonales en cada plano de simetría de Coxeter)

Un 8			B8​						D8​
8-símplex {3,3,3,3,3,3,3}			8 cubos {4,3,3,3,3,3,3}			8-ortoplex {3,3,3,3,3,3,4}		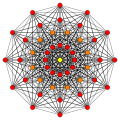	8-demicubes h{4,3,3,3,3,3,3}
E8​
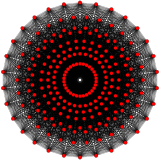4 21 {3,3,3,3,3 2,1 }				2 41 {3,3,3 4,1 }		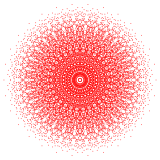		1 42 {3,3 4,2 }

La 7-esfera o hiperesfera en ocho dimensiones es la superficie heptadimensional equidistante de un punto, por ejemplo el origen. Tiene símbolo S ⁷ , con definición formal para la 7-esfera con radio r de$${\displaystyle S^{7}=\left\{x\in \mathbb {R} ^{8}:\|x\|=r\right\}.}$$

El volumen del espacio delimitado por esta 7-esfera es 4.05871 × r ⁸ , o 0.01585 del 8-cubo que contiene la 7-esfera.$${\displaystyle V_{8}\,={\frac {\pi ^{4}}{24}}\,R^{8}}$$

El problema del número del beso se ha resuelto en ocho dimensiones gracias a la existencia del politopo 4 ₂₁ y su red asociada . El número del beso en ocho dimensiones es 240 .

Los octoniones son un álgebra de división normada sobre los números reales, la mayor de estas álgebras. Matemáticamente, se pueden especificar mediante 8-tillos de números reales, por lo que forman un espacio vectorial de 8 dimensiones sobre los reales, siendo la adición de vectores la adición en el álgebra. Un álgebra normada es aquella cuyo producto satisface

${\displaystyle \|xy\|\leq \|x\|\|y\|}$

para todos los x e y en el álgebra. Un álgebra de división normada debe ser además de dimensión finita y tener la propiedad de que cada vector distinto de cero tiene un inverso multiplicativo único. El teorema de Hurwitz prohíbe que una estructura de este tipo exista en dimensiones distintas de 1, 2, 4 u 8.

Los cuaterniones complejizados , o " biquaterniones ", son un álgebra de ocho dimensiones que data del trabajo de William Rowan Hamilton en la década de 1850. Esta álgebra es equivalente (es decir, isomorfa ) al álgebra de Clifford y al álgebra de Pauli . También se ha propuesto como una herramienta práctica o pedagógica para hacer cálculos en relatividad especial , y en ese contexto se la conoce con el nombre de Álgebra del espacio físico (que no debe confundirse con el álgebra del espacio-tiempo , que es de 16 dimensiones).${\displaystyle \mathbb {C} \otimes \mathbb {H} }$ ${\displaystyle C\ell _{2}(\mathbb {C} )}$

• HSM Coxeter :
  • HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
• Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 Wiley::Caleidoscopios: escritos selectos de HSM Coxeter
  • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
  • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
• Tabla de los números de besos más altos conocidos en la actualidad, mantenida por Gabriele Nebe y Neil Sloane (límites inferiores)
• Conway, John Horton ; Smith, Derek A. (2003), Sobre cuaterniones y octoniones: su geometría, aritmética y simetría , AK Peters, Ltd., ISBN 1-56881-134-9. (Revisar).
• Duplij, Steven [en ucraniano] ; Siegel , Warren; Bagger, Jonathan, eds. (2005), Enciclopedia concisa de supersimetría y estructuras no conmutativas en matemáticas y física , Berlín, Nueva York: Springer , ISBN 978-1-4020-1338-6(Segunda impresión)