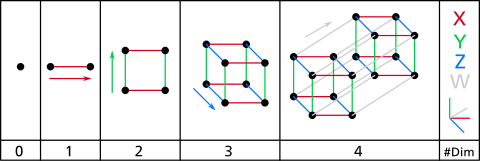Teseracto

Tesseract de 8 celdas (4 cubos)
Tipo	Politopo cuatripartito regular convexo
Símbolo de Schläfli	{4,3,3} t 0,3 {4,3,2} o {4,3}×{ } t 0,2 {4,2,4} o {4}×{4} t 0,2,3 {4,2,2} o {4}×{ }×{ } t 0,1,2,3 {2,2,2} o { }×{ }×{ }×{ }
Diagrama de Coxeter
Células	8 {4,3}
Caras	24 {4}
Bordes	32
Vértices	16
Figura de vértice	Tetraedro
Polígono de Petrie	octágono
Grupo Coxeter	B 4 , [3,3,4]
Dual	16 celdas
Propiedades	politopo convexo , isogonal , isotoxal , isoédrico , de Hanner
Índice uniforme	10

Busque teseracto en Wikcionario, el diccionario libre.

En geometría , un teseracto o 4-cubo es un hipercubo de cuatro dimensiones , análogo a un cuadrado bidimensional y a un cubo tridimensional . ^[1] Así como el perímetro del cuadrado consta de cuatro aristas y la superficie del cubo consta de seis caras cuadradas , la hipersuperficie del teseracto consta de ocho celdas cúbicas , que se encuentran en ángulos rectos . El teseracto es uno de los seis 4-politopos regulares convexos .

El teseracto también se denomina octacoro de 8 celdas , C ₈ , (regular) o prisma cúbico . Es el politopo de medida de cuatro dimensiones , tomado como unidad de hipervolumen. ^[2] Coxeter lo denomina politopo γ ₄ . ^[3] El término hipercubo sin una referencia de dimensión se trata con frecuencia como sinónimo de este politopo específico .

El Oxford English Dictionary rastrea la palabra tesseract hasta el libro de Charles Howard Hinton de 1888 Una nueva era del pensamiento . El término deriva del griego téssara ( τέσσαρα 'cuatro') y aktís ( ἀκτίς 'rayo'), haciendo referencia a las cuatro aristas desde cada vértice hasta otros vértices. Hinton originalmente deletreó la palabra como tessaract . ^[4]

Como politopo regular con tres cubos plegados juntos alrededor de cada arista, tiene el símbolo de Schläfli {4,3,3} con simetría hiperoctaédrica de orden 384. Construido como un hiperprisma 4D hecho de dos cubos paralelos, puede ser nombrado como un símbolo de Schläfli compuesto {4,3} × { }, con orden de simetría 96. Como duoprisma 4-4 , un producto cartesiano de dos cuadrados , puede ser nombrado por un símbolo de Schläfli compuesto {4} × {4}, con orden de simetría 64. Como ortótopo puede ser representado por el símbolo de Schläfli compuesto { } × { } × { } × { } o { } ⁴ , con orden de simetría 16.

Como cada vértice de un teseracto es adyacente a cuatro aristas, la figura del vértice del teseracto es un tetraedro regular . El politopo dual del teseracto es el poliedro de 16 celdas con el símbolo de Schläfli {3,3,4}, con el que se puede combinar para formar el compuesto de teseracto y 16 celdas.

Cada arista de un teseracto regular tiene la misma longitud. Esto es interesante cuando se utilizan teseractos como base para una topología de red para vincular múltiples procesadores en computación paralela : la distancia entre dos nodos es de 4 como máximo y hay muchos caminos diferentes para permitir el equilibrio de peso.

Un teseracto está delimitado por ocho hiperplanos tridimensionales . Cada par de hiperplanos no paralelos se interseca para formar 24 caras cuadradas. Tres cubos y tres cuadrados se intersecan en cada arista. Hay cuatro cubos, seis cuadrados y cuatro aristas que se encuentran en cada vértice. En total, un teseracto consta de 8 cubos, 24 cuadrados, 32 aristas y 16 vértices.

Un teseracto unitario tiene una longitud de lado de 1 y se toma típicamente como la unidad básica para el hipervolumen en un espacio de 4 dimensiones. El teseracto unitario en un sistema de coordenadas cartesianas para un espacio de 4 dimensiones tiene dos vértices opuestos en las coordenadas [0, 0, 0, 0] y [1, 1, 1, 1] y otros vértices con coordenadas en todas las combinaciones posibles de 0 y 1. Es el producto cartesiano del intervalo unitario cerrado [0, 1] en cada eje.

A veces, un teseracto unitario está centrado en el origen, de modo que sus coordenadas son más simétricas. Este es el producto cartesiano del intervalo cerrado en cada eje.${\displaystyle {\bigl (}{\pm {\tfrac {1}{2}}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}}{\bigr )}.}$${\displaystyle {\bigl [}{-{\tfrac {1}{2}}},{\tfrac {1}{2}}{\bigr ]}}$

Otro teseracto que suele ser muy útil es el producto cartesiano del intervalo cerrado [−1, 1] en cada eje, con vértices en las coordenadas (±1, ±1, ±1, ±1) . Este teseracto tiene una longitud de lado de 2 y un hipervolumen de 2 ⁴ = 16 .

Un despliegue de un politopo se denomina red . Hay 261 redes distintas del teseracto. ^[5] Los despliegues del teseracto se pueden contar asignando las redes a árboles pareados (un árbol junto con una correspondencia perfecta en su complemento ).

La construcción de hipercubos se puede imaginar de la siguiente manera:

• Unidimensional: Dos puntos A y B se pueden conectar para formar una línea, dando lugar a un nuevo segmento de línea AB.
• Bidimensional: Dos segmentos de línea paralelos AB y CD separados por una distancia AB se pueden conectar para formar un cuadrado, con las esquinas marcadas como ABCD.
• Tridimensional: Dos cuadrados paralelos ABCD y EFGH separados por una distancia AB se pueden conectar para formar un cubo, con las esquinas marcadas como ABCDEFGH.
• 4-dimensional: Dos cubos paralelos ABCDEFGH e IJKLMNOP separados por una distancia AB pueden conectarse para formar un teseracto, con las esquinas marcadas como ABCDEFGHIJKLMNOP. Sin embargo, esta posición paralela de dos cubos de manera que sus 8 pares de vértices correspondientes estén separados por una distancia AB solo puede lograrse en un espacio de 4 o más dimensiones.

Las 8 celdas del teseracto pueden considerarse (de tres maneras diferentes) como dos anillos entrelazados de cuatro cubos. ^[6]

El teseracto se puede descomponer en politopos de 4 dimensiones más pequeños. Es la envoltura convexa del compuesto de dos teseractos demitacos ( 16 celdas ). También se puede triangular en símplices de 4 dimensiones ( 5 celdas irregulares ) que comparten sus vértices con el teseracto. Se sabe que hay92 487 256 triangulaciones de este tipo ^[7] y que la menor cantidad de símplices de 4 dimensiones en cualquiera de ellas es 16. ^[8]

La disección del teseracto en instancias de su símplex característico (un ortoesquema particular con diagrama de Coxeter)) es la construcción directa más básica posible del teseracto. La característica de 5 celdas del 4-cubo es una región fundamental del grupo de simetría definitorio del teseracto , el grupo que genera los politopos B ₄ . El símplex característico del teseracto genera directamente el teseracto a través de las acciones del grupo, al reflejarse en sus propias facetas delimitadoras (sus paredes especulares ).

El radio de una hiperesfera circunscrita a un politopo regular es la distancia desde el centro del politopo hasta uno de los vértices, y para el teseracto este radio es igual a la longitud de su arista; el diámetro de la esfera, la longitud de la diagonal entre vértices opuestos del teseracto, es el doble de la longitud de la arista. Solo unos pocos politopos uniformes tienen esta propiedad, incluidos el teseracto de cuatro dimensiones y de 24 celdas , el cuboctaedro tridimensional y el hexágono bidimensional . En particular, el teseracto es el único hipercubo (aparte de un punto de dimensión cero) que es radialmente equilátero . La diagonal de vértice a vértice más larga de un hipercubo de una dimensión con una longitud de arista unitaria es que para el cuadrado es para el cubo es y solo para el teseracto es longitudes de arista.${\estilo de visualización n}$${\displaystyle {\sqrt {n{\vphantom {t}}}},}$${\displaystyle {\sqrt {2}},}$${\displaystyle {\sqrt {3}},}$${\displaystyle {\sqrt {4}}=2}$

Un teseracto alineado con el eje inscrito en una 3-esfera de radio unitario tiene vértices con coordenadas${\displaystyle {\bigl (}{\pm {\tfrac {1}{2}}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}}{\bigr )}.}$

Para un teseracto con longitud lateral s :

• Hipervolumen (4D):$Estilo de visualización H=s^{4}}$
• Volumen de superficie (3D):$Estilo de visualización SV=8s^{3}}$
• Diagonal de la cara :${\displaystyle d_{\mathrm {2}}={\sqrt {2}}s}$
• Diagonal de celda :${\displaystyle d_{\mathrm {3}}={\sqrt {3}}s}$
• Diagonal de 4 espacios:${\displaystyle d_{\mathrm {4} }=2s}$

Esta matriz de configuración representa el teseracto. Las filas y columnas corresponden a vértices, aristas, caras y celdas. Los números de la diagonal indican cuántos elementos de cada tipo hay en todo el teseracto. La diagonal se reduce al vector f (16,32,24,8).

Los números no diagonales indican cuántos elementos de la columna se encuentran en o en el elemento de la fila. ^[9] Por ejemplo, el 2 en la primera columna de la segunda fila indica que hay 2 vértices en (es decir, en los extremos de) cada arista; el 4 en la segunda columna de la primera fila indica que 4 aristas se encuentran en cada vértice.

La fila inferior define las facetas, en este caso cubos, que tienen el vector f (8,12,6). La fila siguiente a la izquierda de la diagonal son los elementos de cresta (faceta del cubo), en este caso un cuadrado (4,4).

La fila superior es el vector f de la figura de vértice , en este caso tetraedros (4,6,4). La fila siguiente es la cresta de la figura de vértice, en este caso un triángulo (3,3).

${\displaystyle {\begin{bmatrix}{\begin{matrix}16&4&6&4\\2&32&3&3\\4&4&24&2\\8&12&6&8\end{matrix}}\end{bmatrix}}}$

Es posible proyectar teseractos en espacios tridimensionales y bidimensionales, de forma similar a proyectar un cubo en un espacio bidimensional.

La proyección paralela de las primeras celdas del teseracto en el espacio tridimensional tiene una envoltura cúbica . Las celdas más cercanas y más lejanas se proyectan sobre el cubo, y las seis celdas restantes se proyectan sobre las seis caras cuadradas del cubo.

La proyección paralela de las caras del teseracto en el espacio tridimensional tiene una envoltura cúbica . Dos pares de celdas se proyectan hacia las mitades superior e inferior de esta envoltura, y las cuatro celdas restantes se proyectan hacia las caras laterales.

La proyección paralela de aristas primero del teseracto en el espacio tridimensional tiene una envoltura en forma de prisma hexagonal . Seis celdas se proyectan sobre prismas rómbicos, que están dispuestos en el prisma hexagonal de manera análoga a cómo las caras del cubo 3D se proyectan sobre seis rombos en una envoltura hexagonal bajo proyección de vértice primero. Las dos celdas restantes se proyectan sobre las bases del prisma.

La proyección paralela de vértice primero del teseracto en el espacio tridimensional tiene una envoltura dodecaédrica rómbica . Dos vértices del teseracto se proyectan al origen. Hay exactamente dos maneras de diseccionar un dodecaedro rómbico en cuatro romboedros congruentes, lo que da un total de ocho romboedros posibles, cada uno de ellos un cubo proyectado del teseracto. Esta proyección es también la que tiene el volumen máximo. Un conjunto de vectores de proyección son u = (1,1,−1,−1) , v = (−1,1,−1,1) , w = (1,−1,−1,1) .

Proyecciones ortográficas

Avión Coxeter	B4​	B4 -- > A3	Un 3
Gráfico
Simetría diedral	[8]	[4]	[4]
Avión Coxeter	Otro	B3 / D4 / A2​	B2 / D3​
Gráfico
Simetría diedral	[2]	[6]	[4]

Proyección en 3D de un teseracto que realiza una rotación simple sobre un plano en un espacio de cuatro dimensiones. El plano divide la figura en dos, de adelante hacia atrás, de izquierda a derecha, y de arriba hacia abajo.

Una proyección 3D de un teseracto que realiza una doble rotación alrededor de dos planos ortogonales en un espacio de 4 dimensiones.

Perspectiva con eliminación de volumen oculto . La esquina roja es la más cercana en 4D y tiene 4 celdas cúbicas que se unen a su alrededor.

El tetraedro forma la envoltura convexa de la proyección central centrada en el vértice del teseracto. Se muestran cuatro de las ocho celdas cúbicas. El decimosexto vértice se proyecta al infinito y no se muestran las cuatro aristas que lo delimitan.

Proyección estereográfica (Los bordes se proyectan sobre la esfera tridimensional )

Proyección estereoscópica 3D de un teseracto (vista paralela)

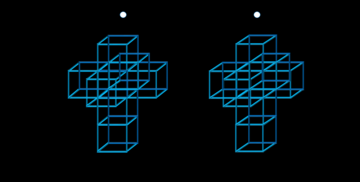Hipercubo desarmado estereoscópico 3D

El teseracto, como todos los hipercubos , tesela el espacio euclidiano . El panal teseractico autodual que consta de 4 teseractos alrededor de cada cara tiene el símbolo de Schläfli {4,3,3,4} . Por lo tanto, el teseracto tiene un ángulo diedro de 90°. ^[10]

La simetría equilátera radial del teseracto hace que su teselación sea la única red cúbica regular centrada en el cuerpo de esferas de igual tamaño, en cualquier número de dimensiones.

El teseracto es el cuarto de una serie de hipercubos :

Proyecciones ortográficas del polígono de Petrie

Segmento de línea	Cuadrado	Cubo	4 cubos	5 cubos	6 cubos	7 cubos	8 cubos	9 cubos	10 cubos

El teseracto (de 8 celdas) es el tercero de la secuencia de 6 4-politopos regulares convexos (en orden de tamaño y complejidad).

Politopos cuatripartitos convexos regulares
Grupo de simetría	Un 4	B4​		F4​	H4​
Nombre	5 celdas Hipertetraedro de 5 puntas	16 celdas Hiper - octaedro de 8 puntas	8 celdas Hipercubo de 16 puntos	24 celdas 24 puntos	600 celdas Hipericosaedro de 120 puntos	120 celdas Hiperdodecaedro de 600 puntos
Símbolo de Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Espejos Coxeter
Diédricos especulares	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
Gráfico
Vértices	5 tetraédricos	8 octaédrico	16 tetraédrico	24 cúbicos	120 icosaédricos	600 tetraédricos
Bordes	10 triangular	24 cuadrados	32 triangular	96 triangular	720 pentagonal	1200 triangular
Caras	10 triángulos	32 triángulos	24 cuadrados	96 triángulos	1200 triángulos	720 pentágonos
Células	5 tetraedros	16 tetraedros	8 cubos	24 octaedros	600 tetraedros	120 dodecaedros
Toros	1 5-tetraedro	2 8-tetraedro	2 4 cubos	4 6-octaedro	20 30-tetraedro	12 10-dodecaedro
Inscrito	120 en 120 celdas	675 en 120 celdas	2 de 16 celdas	3 de 8 celdas	25 24 celdas	10 600 celdas
Grandes polígonos		2 cuadrados x 3	4 rectángulos x 4	4 hexágonos x 4	12 decágonos x 6	100 hexágonos irregulares x 4
Polígonos de Petrie	1 pentágono x 2	1 octágono x 3	2 octágonos x 4	2 dodecágonos x 4	4 30-ágonos x 6	20 30-ágonos x 4
Radio largo	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$
Longitud del borde	${\displaystyle {\sqrt {\tfrac {5}{2}}}\aproximadamente 1,581}$	${\displaystyle {\sqrt {2}}\aproximadamente 1,414}$	${\estilo de visualización 1}$	${\estilo de visualización 1}$	${\displaystyle {\tfrac {1}{\phi }}\aproximadamente 0,618}$	${\displaystyle {\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\aproximadamente 0,270}$
Radio corto	${\displaystyle {\frac {1}{4}}}$	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\sqrt {\tfrac {1}{2}}}\aproximadamente 0,707}$	${\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\aproximadamente 0,926}$	${\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\aproximadamente 0,926}$
Área	${\displaystyle 10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\aproximadamente 10,825}$	${\displaystyle 32\left({\sqrt {\tfrac {3}{4}}}\right)\aproximadamente 27,713}$	${\estilo de visualización 24}$	${\displaystyle 96\left({\sqrt {\tfrac {3}{16}}}\right)\aproximadamente 41,569}$	${\displaystyle 1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\aproximadamente 198,48}$	${\displaystyle 720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\aproximadamente 90,366}$
Volumen	${\displaystyle 5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\aproximadamente 2,329}$	${\displaystyle 16\left({\tfrac {1}{3}}\right)\aproximadamente 5,333}$	${\estilo de visualización 8}$	${\displaystyle 24\left({\tfrac {\sqrt {2}}{3}}\right)\aproximadamente 11,314}$	${\displaystyle 600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\aproximadamente 16,693}$	${\displaystyle 120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\aproximadamente 18,118}$
4-Contenido	${\displaystyle {\tfrac {\sqrt {5}}{24}}\izquierda({\tfrac {\sqrt {5}}{2}}\derecha)^{4}\aproximadamente 0,146}$	${\displaystyle {\tfrac {2}{3}}\aproximadamente 0,667}$	${\estilo de visualización 1}$	${\estilo de visualización 2}$	${\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863}$	${\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193}$

Como duoprisma uniforme , el teseracto existe en una secuencia de duoprismas uniformes : { p }×{4}.

El teseracto regular, junto con el de 16 celdas , existe en un conjunto de 15 4-politopos uniformes con la misma simetría . El teseracto {4,3,3} existe en una secuencia de 4-politopos y panales regulares , { p ,3,3} con figuras de vértices tetraédricas , {3,3}. El teseracto también está en una secuencia de 4-politopos y panales regulares , {4,3, p } con celdas cúbicas .

Ortogonal	Perspectiva
4 {4} 2 , con 16 vértices y 8 aristas de 4, con las 8 aristas de 4 mostradas aquí como 4 cuadrados rojos y 4 azules

El politopo complejo regular ₄ {4} ₂ ,, tiene una representación real como un teseracto o duoprisma 4-4 en un espacio de 4 dimensiones. ₄ {4} ₂ tiene 16 vértices y 8 aristas de 4 dimensiones. Su simetría es ₄ [4] ₂ , orden 32. También tiene una construcción de simetría inferior,${\displaystyle \mathbb {C} ^{2}}$, o ₄ {}× ₄ {}, con simetría ₄ [2] ₄ , orden 16. Esta es la simetría si los 4 bordes rojo y azul se consideran distintos. ^[11]

Desde su descubrimiento, los hipercubos de cuatro dimensiones han sido un tema popular en el arte, la arquitectura y la ciencia ficción. Algunos ejemplos notables incluyen:

• " Y construyó una casa torcida ", la historia de ciencia ficción de Robert Heinlein de 1940 que presenta un edificio en forma de hipercubo de cuatro dimensiones. ^[12] Este y "El profesor sin lados" de Martin Gardner , publicado en 1946, se encuentran entre los primeros en ciencia ficción en presentar a los lectores la banda de Moebius , la botella de Klein y el hipercubo (teseracto).
• Crucifixión (Corpus Hypercubus) , una pintura al óleo de 1954 de Salvador Dalí que presenta un hipercubo de cuatro dimensiones desplegado en una cruz latina tridimensional. ^[13]
• El Gran Arco , un monumento y edificio cerca de París, Francia, terminado en 1989. Según el ingeniero del monumento, Erik Reitzel , el Gran Arco fue diseñado para parecerse a la proyección de un hipercubo. ^[14]
• Fez , un videojuego en el que uno juega con un personaje que puede ver más allá de las dos dimensiones que otros personajes pueden ver, y debe usar esta habilidad para resolver acertijos de plataformas. Presenta a "Dot", un teseracto que ayuda al jugador a navegar por el mundo y le dice cómo usar habilidades, lo que se ajusta al tema de ver más allá de la percepción humana del espacio dimensional conocido. ^[15]

La palabra teseracto ha sido adoptada para numerosos otros usos en la cultura popular, incluso como recurso argumental en obras de ciencia ficción, a menudo con poca o ninguna conexión con el hipercubo de cuatro dimensiones; véase Teseracto (desambiguación) .

• Matemáticas y arte

• Coxeter, HSM (1973). Politopos regulares (3.ª ed.). Nueva York: Dover. pp. 122–123.
• F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) Caleidoscopios: escritos seleccionados de HSM Coxeter , Wiley-Interscience Publication ISBN 978-0-471-01003-6 [1] 
  • (Documento 22) HSM Coxeter, Politopos regulares y semiregulares I , Mathematische Zeitschrift 46 (1940) 380–407, MR 2,10]
  • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
  • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
• Coxeter, HSM (1970), "Panales retorcidos", Serie de conferencias regionales sobre matemáticas del Conference Board of the Mathematical Sciences , 4 , Providence, Rhode Island: American Mathematical Society
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss (2008) Las simetrías de las cosas , ISBN 978-1-56881-220-5 (Capítulo 26, págs. 409: Hemicubos: 1 _n1 ) 
• T. Gosset (1900) Sobre las figuras regulares y semirregulares en el espacio de n dimensiones , Messenger of Mathematics , Macmillan.
• Hall, T. Proctor (1893). "La proyección de figuras cuádruples sobre un plano de tres". American Journal of Mathematics . 15 (2): 179–189. doi :10.2307/2369565. JSTOR  2369565.
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. (1966)
• Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper , Waren.

• Klitzing, Richard. "Polítopos uniformes 4D (policoros) x4o3o3o - tes".
• Página de inicio de Ken Perlin Una forma de visualizar hipercubos, por Ken Perlin
• Algunas notas sobre la cuarta dimensión incluye tutoriales animados sobre varios aspectos diferentes del teseracto, por Davide P. Cervone
• Animación de Tesseract con eliminación de volumen oculto

Proyecciones ortográficas del polígono de Petrie

Segmento de línea	Cuadrado	Cubo	4 cubos	5 cubos	6 cubos	7 cubos	8 cubos	9 cubos	10 cubos