Teseracto truncado

Teseracto	Teseracto truncado	Teseracto rectificado	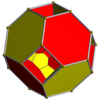Teseracto bitruncado
Diagramas de Schlegel centrados en [4,3] (celdas visibles en [3,3])
16 celdas	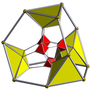16 celdas truncadas	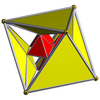Rectificado de 16 celdas ( 24 celdas )	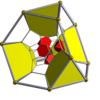Teseracto bitruncado
Diagramas de Schlegel centrados en [3,3] (celdas visibles en [4,3])

En geometría , un teseracto truncado es un politopo uniforme de 4 elementos formado como el truncamiento del teseracto regular .

Hay tres truncamientos, incluido un bitruncation y un tritruncamiento, que crea el truncamiento de 16 celdas .

Teseracto truncado
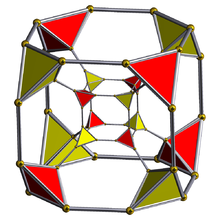Diagrama de Schlegel ( células tetraédricas visibles)
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t{4,3,3}
Diagramas de Coxeter
Células	24	8 3.8.8 16 3.3.3
Caras	88	64 {3} 24 {8}
Bordes	128
Vértices	64
Figura de vértice	( )v{3}
Dual	Tetrakis de 16 células
Grupo de simetría	B 4 , [4,3,3], orden 384
Propiedades	convexo
Índice uniforme	12 13 14

El teseracto truncado está delimitado por 24 celdas : 8 cubos truncados y 16 tetraedros .

• Teseracto truncado ( Norman W. Johnson )
• Teseracto truncado (acrónimo tat) (George Olshevsky y Jonathan Bowers) ^[1]

El teseracto truncado se puede construir truncando los vértices del teseracto en la longitud de la arista. Se forma un tetraedro regular en cada vértice truncado.${\displaystyle 1/({\sqrt {2}}+2)}$

Las coordenadas cartesianas de los vértices de un teseracto truncado con una longitud de arista de 2 se dan mediante todas las permutaciones de:

${\displaystyle \left(\pm 1,\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}})\right)}$

En la primera proyección paralela del cubo truncado del teseracto truncado en el espacio tridimensional, la imagen se presenta de la siguiente manera:

• La envolvente de proyección es un cubo .
• Dos de las celdas del cubo truncado se proyectan sobre un cubo truncado inscrito en la envoltura cúbica.
• Los otros 6 cubos truncados se proyectan sobre las caras cuadradas del sobre.
• Los 8 volúmenes tetraédricos entre la envoltura y las caras triangulares del cubo truncado central son las imágenes de los 16 tetraedros, un par de celdas para cada imagen.

proyecciones ortográficas

Avión Coxeter	B4​	B3 / D4 / A2​	B2 / D3​
Gráfico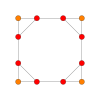
Simetría diedral	[8]	[6]	[4]
Avión Coxeter	F4​	Un 3
Gráfico
Simetría diedral	[12/3]	[4]

Una red poliédrica

Teseracto truncado proyectado sobre la 3-esfera con una proyección estereográfica en el 3-espacio.

El teseracto truncado es el tercero de una secuencia de hipercubos truncados :

Hipercubos truncados

Imagen								...
Nombre	Octágono	Cubo truncado	Teseracto truncado	Cubo truncado de 5	Cubo truncado de 6	Cubo 7 truncado	Cubo 8 truncado
Diagrama de Coxeter
Figura de vértice	( )v( )	( )v{ }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3,3}	( )v{3,3,3,3,3}

Teseracto bitruncado
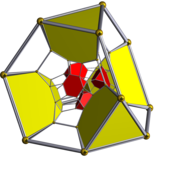Dos diagramas de Schlegel , centrados en células tetraédricas u octaédricas truncadas, con tipos de células alternativos ocultos.
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	2t{4,3,3} 2t{3,3 1,1 } h 2,3 {4,3,3}
Diagramas de Coxeter	=
Células	24	8 4.6.6 16 3.6.6
Caras	120	32 {3} 24 {4} 64 {6}
Bordes	192
Vértices	96
Figura de vértice	Difenoide digonal
Grupo de simetría	B 4 , [3,3,4], orden 384 D 4 , [3 1,1,1 ], orden 192
Propiedades	convexo , transitivo de vértice
Índice uniforme	15 16 17

El teseracto bitruncado , bitruncado de 16 celdas o teseractihexadecacoron se construye mediante una operación de bitruncación aplicada al teseracto . También se lo puede llamar teseracto runcicántico con la mitad de los vértices de un teseracto runcicantelado con unconstrucción.

• Teseracto bitruncado/teseracto runicántico ( Norman W. Johnson )
• Tesseractihexadecachoron (acrónimo tah) (George Olshevsky y Jonathan Bowers) ^[2]

Un teseracto se bitrunca truncando sus celdas más allá de sus puntos medios, convirtiendo los ocho cubos en ocho octaedros truncados . Estos aún comparten sus caras cuadradas, pero las caras hexagonales forman tetraedros truncados que comparten sus caras triangulares entre sí.

Las coordenadas cartesianas de los vértices de un teseracto bitruncado que tiene una longitud de arista de 2 se dan mediante todas las permutaciones de:

${\displaystyle \left(0,\ \pm {\sqrt {2}},\ \pm 2{\sqrt {2}},\ \pm 2{\sqrt {2}}\right)}$

Los octaedros truncados están conectados entre sí por sus caras cuadradas, y con los tetraedros truncados por sus caras hexagonales. Los tetraedros truncados están conectados entre sí por sus caras triangulares.

proyecciones ortográficas

Avión Coxeter	B4​	B3 / D4 / A2​	B2 / D3​
Gráfico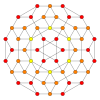
Simetría diedral	[8]	[6]	[4]
Avión Coxeter	F4​	Un 3
Gráfico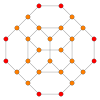
Simetría diedral	[12/3]	[4]

La proyección del octaedro truncado primero del teseracto bitruncado en el espacio 3D tiene una envoltura cúbica truncada . Dos de las celdas octaédricas truncadas se proyectan sobre un octaedro truncado inscrito en esta envoltura, con las caras cuadradas tocando los centros de las caras octaédricas. Las 6 caras octaédricas son las imágenes de las 6 celdas octaédricas truncadas restantes. El espacio restante entre el octaedro truncado inscrito y la envoltura está ocupado por 8 tetraedros truncados aplanados, cada uno de los cuales es la imagen de un par de celdas tetraédricas truncadas.

Proyecciones estereográficas

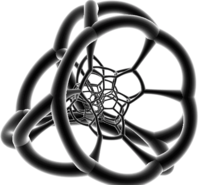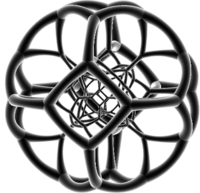Coloreado de forma transparente con triángulos rosas, cuadrados azules y hexágonos grises.

El teseracto bitruncado es el segundo en una secuencia de hipercubos bitruncados :

Hipercubos bitruncados

Imagen							...
Nombre	Cubo bitruncado	Teseracto bitruncado	5 cubos bitruncados	Cubo de 6 bits truncado	Cubo de 7 bits truncado	Cubo de 8 bits truncado
Coxeter
Figura de vértice	( )v{ }	{ }v{ }	{ }v{3}	{ }v{3,3}	{ }v{3,3,3}	{ }v{3,3,3,3}

Teseracto cántico truncado de 16 celdas
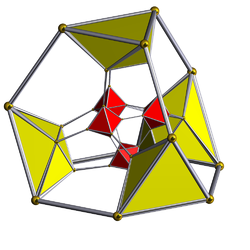Diagrama de Schlegel ( células del octaedro visibles)
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t {4,3,3} t{3,3 1,1 } h2 {4,3,3}
Diagramas de Coxeter	=
Células	24	8 3.3.3.3 16 3.6.6
Caras	96	64 {3} 32 {6}
Bordes	120
Vértices	48
Figura de vértice	pirámide cuadrada
Dual	Teseracto de Hexakis
Grupos de Coxeter	B 4 [3,3,4], orden 384 D 4 [3 1,1,1 ], orden 192
Propiedades	convexo
Índice uniforme	16 17 18

El teseracto cántico truncado de 16 celdas , hexadecacoron truncado , que está limitado por 24 celdas : 8 octaedros regulares y 16 tetraedros truncados . Tiene la mitad de los vértices de un teseracto cantelado con construcción.

Está relacionado con el politopo de 24 celdas , pero no debe confundirse con él , que es un politopo regular de 4 elementos delimitado por 24 octaedros regulares.

• Teseracto cántico de dieciséis celdas truncado ( Norman W. Johnson )
• Hexadecacoron truncado (acrónimo thex) (George Olshevsky y Jonathan Bowers) ^[3]

El sistema de 16 celdas truncadas se puede construir a partir de las 16 celdas truncando sus vértices en 1/3 de la longitud de la arista. Esto da como resultado las 16 celdas tetraédricas truncadas y presenta los 8 octaedros (figuras de vértices).

(Al truncar una celda de 16 a la mitad de la longitud del borde se obtiene una celda de 24 , que tiene un mayor grado de simetría porque las celdas truncadas se vuelven idénticas a las figuras de los vértices).

Las coordenadas cartesianas de los vértices de una celda truncada de 16 que tiene una longitud de arista de √2 se dan mediante todas las permutaciones y combinaciones de signos de

(0,0,1,2)

Una construcción alternativa comienza con un semiteseracto con coordenadas de vértice (±3,±3,±3,±3), que tiene un número par de cada signo, y lo trunca para obtener las permutaciones de

(1,1,3,3), con un número par de cada signo.

Los tetraedros truncados están unidos entre sí por sus caras hexagonales. Los octaedros están unidos a los tetraedros truncados por sus caras triangulares.

La proyección paralela del octaedro primero de la celda truncada de 16 en el espacio tridimensional tiene la siguiente estructura:

• La envolvente de proyección es un octaedro truncado .
• Las 6 caras cuadradas de la envolvente son las imágenes de 6 de las celdas octaédricas.
• En el centro de la envoltura se encuentra un octaedro, unido al centro de las 6 caras cuadradas por 6 aristas. Esta es la imagen de las otras 2 celdas octaédricas.
• El espacio restante entre la envoltura y el octaedro central está ocupado por 8 tetraedros truncados (distorsionados por la proyección). Éstas son las imágenes de las 16 celdas tetraédricas truncadas, un par de celdas por cada imagen.

Esta disposición de las celdas en la proyección es análoga a la disposición de las caras en la proyección del octaedro truncado en el espacio bidimensional. Por lo tanto, el truncado de 16 celdas puede considerarse el análogo en cuatro dimensiones del octaedro truncado.

La primera proyección paralela del tetraedro truncado de 16 celdas en el espacio tridimensional tiene la siguiente estructura:

• La envolvente de proyección es un cubo truncado .
• El tetraedro truncado más cercano al punto de vista 4D se proyecta hacia el centro de la envolvente, con sus caras triangulares unidas a 4 volúmenes octaédricos que lo conectan a 4 de las caras triangulares de la envolvente.
• El espacio restante en la envoltura está ocupado por otros cuatro tetraedros truncados.
• Estos volúmenes son las imágenes de las celdas que se encuentran en el lado cercano de las 16 celdas truncadas; las otras celdas se proyectan sobre la misma disposición excepto en la configuración dual.
• Las seis caras octogonales de la envolvente de proyección son las imágenes de las 6 celdas tetraédricas truncadas restantes.

proyecciones ortográficas

Avión Coxeter	B4​	B3 / D4 / A2​	B2 / D3​
Gráfico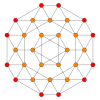
Simetría diedral	[8]	[6]	[4]
Avión Coxeter	F4​	Un 3
Gráfico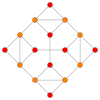
Simetría diedral	[12/3]	[4]

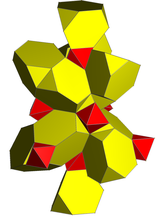Neto	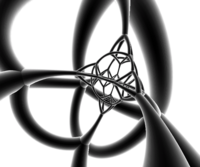Proyección estereográfica (centrada en el tetraedro truncado )

Un truncamiento de 16 celdas, como un 4-cubo cántico, está relacionado con la familia dimensional de n-cubos cánticos:

Familia dimensional de n-cubos cánticos

norte	3	4	5	6	7	8
Simetría [1 + ,4,3 n-2 ]	[1 + ,4,3] = [3,3]	[1 + ,4,3 2 ] = [3,3 1,1 ]	[1 + ,4,3 3 ] = [3,3 2,1 ]	[1 + ,4,3 4 ] = [3,3 3,1 ]	[1 + ,4,3 5 ] = [3,3 4,1 ]	[1 + ,4,3 6 ] = [3,3 5,1 ]
Figura cántica
Coxeter	=	=	=	=	=	=
Colapso	h2 { 4,3}	h2 { 4,32 }​	h2 { 4,33 }​	h2 { 4,3 4 }	h2 { 4,3 5 }	h2 { 4,3 6 }

D 4 policora uniforme
{3,3 1,1 } h{4,3,3}	2r{3,3 1,1 } h3 {4,3,3 }	t{3,3 1,1 } h2 {4,3,3 }	2t{3,3 1,1 } h2,3 { 4,3,3}	r{3,3 1,1 } {3 1,1,1 }={3,4,3}	rr{3,3 1,1 } r{3 1,1,1 }=r{3,4,3}	tr{3,3 1,1 } t{3 1,1,1 }=t{3,4,3}	sr{3,3 1,1 } s{3 1,1,1 }=s{3,4,3}

Politopos de simetría B4
Nombre	teseracto	teseracto rectificado	teseracto truncado	teseracto cantelado	teseracto runcinado	teseracto bitruncado	teseracto truncado	teseracto runcitruncado	teseracto omnitruncado
Diagrama de Coxeter		=				=
Símbolo de Schläfli	{4,3,3}	t1 { 4,3,3 } r{4,3,3}	t0,1 {4,3,3} t { 4,3,3}	t 0,2 {4,3,3} rr{4,3,3}	t0,3 { 4,3,3}	t1,2 {4,3,3} 2t {4,3,3}	t 0,1,2 {4,3,3} tr{4,3,3}	t0,1,3 { 4,3,3}	t0,1,2,3 { 4,3,3}
Diagrama de Schlegel
B4​
Nombre	16 celdas	rectificado de 16 celdas	16 celdas truncadas	cantelado de 16 celdas	Runcinated de 16 celdas	bitruncado de 16 celdas	cantitruncado de 16 celdas	Runcitruncado de 16 celdas	omnitruncado de 16 celdas
Diagrama de Coxeter	=	=	=	=		=	=
Símbolo de Schläfli	{3,3,4}	t1 { 3,3,4 } r{3,3,4}	t0,1 {3,3,4} t { 3,3,4}	t 0,2 {3,3,4} rr{3,3,4}	t0,3 { 3,3,4}	t1,2 {3,3,4} 2t {3,3,4}	t 0,1,2 {3,3,4} tr{3,3,4}	t0,1,3 { 3,3,4}	t0,1,2,3 { 3,3,4}
Diagrama de Schlegel
B4​

• T. Gosset : Sobre las figuras regulares y semirregulares en el espacio de n dimensiones , Messenger of Mathematics, Macmillan, 1900
• HSM Coxeter :
  • Coxeter, Regular Polytopes , (3.ª edición, 1973), edición Dover, ISBN  0-486-61480-8 , pág. 296, Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)
  • HSM Coxeter, Regular Polytopes , 3.ª edición, Dover Nueva York, 1973, pág. 296, Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)
  • Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
    • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
    • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26, págs. 409: Hemicubos: 1 _n1 ) 
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. (1966)
• 2. Polícora uniforme convexa basada en el teseracto (8 celdas) y el hexadecacoron (16 celdas) - Modelos 13, 16, 17, George Olshevsky.
• Klitzing, Richard. "Polítopos uniformes 4D (policora)".o3o3o4o - tat, o3x3x4o - tah, x3x3o4o - thex

• Modelo de papel de teseracto truncado creado utilizando redes generadas por el software Stella4D