Hexágono

Hexágono regular
Un hexágono regular
Tipo	Polígono regular
Aristas y vértices	6
Símbolo de Schläfli	{6}, t{3}
Diagramas de Coxeter-Dynkin
Grupo de simetría	Diédrico (D 6 ), orden 2×6
Angulo interno ( grados )	120°
Propiedades	Convexo , cíclico , equilátero , isogonal , isotoxal
Polígono dual	Ser

En geometría , un hexágono (del griego ἕξ , hex , que significa "seis", y γωνία , gonía , que significa "esquina, ángulo") es un polígono de seis lados . ^[1] El total de los ángulos internos de cualquier hexágono simple (no autointersecante) es 720°.

Un hexágono regular tiene el símbolo de Schläfli {6} ^[2] y también puede construirse como un triángulo equilátero truncado , t{3}, que alterna dos tipos de aristas.

Un hexágono regular se define como un hexágono que es equilátero y equiangular . Es bicéntrico , es decir, es cíclico (tiene un círculo circunscrito) y tangencial (tiene un círculo inscrito).

La longitud común de los lados es igual al radio del círculo circunscrito o circuncírculo , que es igual a veces la apotema (radio del círculo inscrito ). Todos los ángulos internos son de 120 grados . Un hexágono regular tiene seis simetrías rotacionales ( simetría rotacional de orden seis ) y seis simetrías de reflexión ( seis ejes de simetría ), que forman el grupo diedro D ₆ . Las diagonales más largas de un hexágono regular, que conectan vértices diametralmente opuestos, tienen el doble de longitud de un lado. De esto se puede ver que un triángulo con un vértice en el centro del hexágono regular y que comparte un lado con el hexágono es equilátero , y que el hexágono regular se puede dividir en seis triángulos equiláteros.${\displaystyle {\tfrac {2}{\sqrt {3}}}}$

Al igual que los cuadrados y los triángulos equiláteros , los hexágonos regulares encajan entre sí sin dejar espacios vacíos para formar mosaicos en el plano (tres hexágonos que se encuentran en cada vértice), por lo que son útiles para construir teselaciones . Las celdas de un panal de abejas son hexagonales por esta razón y porque la forma hace un uso eficiente del espacio y de los materiales de construcción. El diagrama de Voronoi de una red triangular regular es la teselación en panal de abejas de hexágonos.

El diámetro máximo (que corresponde a la diagonal larga del hexágono), D , es el doble del radio máximo o circunradio , R , que es igual a la longitud del lado, t . El diámetro mínimo o diámetro del círculo inscrito (separación de lados paralelos, distancia de plano a plano, diagonal corta o altura cuando reposa sobre una base plana), d , es el doble del radio mínimo o inradio , r . Los máximos y mínimos están relacionados por el mismo factor:

${\displaystyle {\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t}$   y, de manera similar,${\displaystyle d={\frac {\sqrt {3}}{2}}D.}$

El área de un hexágono regular

${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\[3pt]&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\[3pt]&\aproximadamente 2,598R^{2}\aproximadamente 3,464r^{2}\\&\aproximadamente 0,6495D^{2}\aproximadamente 0,866d^{2}.\end{aligned}}}$

Para cualquier polígono regular , el área también se puede expresar en términos de la apotema a y el perímetro p . Para el hexágono regular, estos valores se dan por a = r y p , por lo que${\displaystyle {}=6R=4r{\sqrt {3}}}$

${\displaystyle {\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{2}}=2r^{2}{\sqrt {3}}\\&\aproximadamente 3,464r^{2}.\end{aligned}}}$

El hexágono regular rellena la fracción de su círculo circunscrito .${\displaystyle {\tfrac {3{\sqrt {3}}}{2\pi }}\aproximadamente 0,8270}$

Si un hexágono regular tiene vértices sucesivos A, B, C, D, E, F y si P es cualquier punto del círculo circunscrito entre B y C, entonces PE + PF = PA + PB + PC + PD .

De la relación entre el radio circunscrito y el radio interno se deduce que la relación entre la altura y el ancho de un hexágono regular es 1:1,1547005; es decir, un hexágono con una diagonal larga de 1,0000000 tendrá una distancia de 0,8660254 entre lados paralelos.

Para un punto arbitrario en el plano de un hexágono regular con radio circunscrito , cuyas distancias al centroide del hexágono regular y sus seis vértices son y respectivamente, tenemos ^[3]${\estilo de visualización R}$${\estilo de visualización L}$$estilo de visualización d_{i}}$

${\displaystyle d_{1}^{2}+d_{4}^{2}=d_{2}^{2}+d_{5}^{2}=d_{3}^{2}+d_{6}^{2}=2\left(R^{2}+L^{2}\right),}$

${\displaystyle d_{1}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{2}+d_{4}^{2}+d_{6}^{2}=3\left(R^{2}+L^{2}\right),}$

${\displaystyle d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{2}^{4}+d_{4}^{4}+d_{6}^{4}=3\left(\left(R^{2}+L^{2}\right)^{2}+2R^{2}L^{2}\right).}$

Si son las distancias desde los vértices de un hexágono regular a cualquier punto de su circunferencia circunscrita, entonces ^[3]$estilo de visualización d_{i}}$

${\displaystyle \left(\suma _{i=1}^{6}d_{i}^{2}\right)^{2}=4\suma _{i=1}^{6}d_{i}^{4}.}$

Ejemplo de hexágonos por simetría
R12 normal i4 d6 isotoxal g6 dirigido p6 isogonal d2 Paralelogono general g2 pág. 2 g3 a1

El hexágono regular tiene simetría D ₆ . Hay 16 subgrupos. Hay 8 hasta el isomorfismo: el propio (D ₆ ), 2 diedros: (D _{3 ,} D ₂ ), 4 cíclicos : (Z ₆ , Z ₃ , Z ₂ , Z ₁ ) y el trivial (e)

Estas simetrías expresan nueve simetrías distintas de un hexágono regular. John Conway las etiqueta con una letra y un orden de grupo. ^[4] r12 es simetría completa y a1 no es simetría. p6 , un hexágono isogonal construido con tres espejos puede alternar aristas largas y cortas, y d6 , un hexágono isotoxal construido con longitudes de arista iguales, pero vértices que alternan dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del hexágono regular. Las formas i4 son hexágonos regulares aplanados o estirados a lo largo de una dirección de simetría. Puede verse como un rombo alargado , mientras que d2 y p2 pueden verse como cometas alargadas horizontal y verticalmente . Los hexágonos g2 , con lados opuestos paralelos, también se denominan paralelogones hexagonales .

Cada subgrupo de simetría permite uno o más grados de libertad para las formas irregulares. Solo el subgrupo g6 no tiene grados de libertad, pero puede verse como aristas dirigidas .

Los hexágonos de simetría g2 , i4 y r12 , como paralelogones , pueden teselar el plano euclidiano por traslación. Otras formas hexagonales pueden teselar el plano con diferentes orientaciones.

pág. 6 m (*632)	cmm (2*22)	pág. 2 (2222)	pág. 31 m (3*3)	pmg (22*)		pág. (××)
r12	i4	g2	d2	d2	pág. 2	a1
Día 6	Di 2	El 2	Di 1			El 1

Raíces del grupo A2

Raíces del grupo G2

Las 6 raíces del grupo de Lie simple A2 , representadas por un diagrama de Dynkin , tienen un patrón hexagonal regular. Las dos raíces simples tienen un ángulo de 120° entre sí.

Las 12 raíces del grupo de Lie excepcional G2 , representadas por un diagrama de Dynkin También tienen un patrón hexagonal. Las dos raíces simples de dos longitudes tienen un ángulo de 150° entre ellas.

Proyección de 6 cubos	12 disección de rombos

Coxeter afirma que cada zonógono (un 2 m -gono cuyos lados opuestos son paralelos y de igual longitud) puede diseccionarse en paralelogramos de 1 ⁄ 2 m ( m − 1) . ^[5] En particular, esto es cierto para polígonos regulares con lados uniformes, en cuyo caso los paralelogramos son todos rombos. Esta descomposición de un hexágono regular se basa en una proyección de polígono de Petrie de un cubo , con 3 de 6 caras cuadradas. Otros paralelogonos y direcciones proyectivas del cubo se disecan dentro de cuboides rectangulares .

Disección de hexágonos en tres rombos y paralelogramos
2D	Rombos	Paralelogramos
	Regular {6}	Paralelogonos hexagonales
3D	Caras cuadradas		Caras rectangulares
	Cubo		Cuboide rectangular

Un hexágono regular tiene el símbolo de Schläfli {6}. Un hexágono regular es una parte del mosaico hexagonal regular , {6,3}, con tres caras hexagonales alrededor de cada vértice.

Un hexágono regular también puede crearse como un triángulo equilátero truncado , con el símbolo de Schläfli t{3}. Vista con dos tipos (colores) de aristas, esta forma solo tiene simetría D _{3 .}

Un hexágono truncado , t{6}, es un dodecágono , {12}, que alterna dos tipos (colores) de aristas. Un hexágono alternado , h{6}, es un triángulo equilátero , {3}. Un hexágono regular se puede estelarizar con triángulos equiláteros en sus aristas, creando un hexagrama . Un hexágono regular se puede dividir en seis triángulos equiláteros añadiendo un punto central. Este patrón se repite dentro del mosaico triangular regular .

Un hexágono regular se puede convertir en un dodecágono regular añadiendo cuadrados y triángulos equiláteros alternados a su alrededor. Este patrón se repite dentro del mosaico rombitrihexagonal .

Regular {6}	T truncado {3} = {6}	Triángulos hipertruncados			Figura de estrella estrellada 2{3}	T truncado {6} = {12}	h{6} alternado = {3}

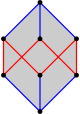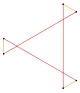
Hexágono cruzado	Un hexágono cóncavo	Un hexágono que se interseca consigo mismo ( polígono estrellado )	Central extendida {6} en {12}	Un hexágono oblicuo , dentro de un cubo	Disecado {6}	octaedro de proyección	Gráfica completa

Hay seis hexágonos autocruzados con la disposición de vértices del hexágono regular:

Hexágonos autointersecantes con vértices regulares

Di 2			Di 1		Di 3
Figura ocho	Giro al centro	Unicursal	Cola de pez	Doble cola	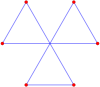Triple cola

Desde los panales de las abejas hasta la Calzada del Gigante , los patrones hexagonales son comunes en la naturaleza debido a su eficiencia. En una cuadrícula hexagonal, cada línea es lo más corta posible si se debe llenar un área grande con la menor cantidad de hexágonos. Esto significa que los panales requieren menos cera para construirse y ganan mucha resistencia bajo compresión .

Los hexágonos irregulares con aristas opuestas y paralelas se denominan paralelogones y también pueden teselar el plano por traslación. En tres dimensiones, los prismas hexagonales con caras opuestas y paralelas se denominan paraleloedros y pueden teselar el espacio tridimensional por traslación.

Teselaciones de prismas hexagonales

Forma	Azulejos hexagonales	Panal prismático hexagonal
Regular
Paralelogonal

Además del hexágono regular, que determina una teselación única del plano, cualquier hexágono irregular que satisfaga el criterio de Conway teselará el plano.

El teorema de Pascal (también conocido como "Teorema del Hexagrammum Mysticum") establece que si se inscribe un hexágono arbitrario en cualquier sección cónica y se extienden pares de lados opuestos hasta que se encuentran, los tres puntos de intersección estarán en una línea recta, la "línea de Pascal" de esa configuración.

El hexágono de Lemoine es un hexágono cíclico (inscrito en un círculo) con vértices dados por las seis intersecciones de las aristas de un triángulo y las tres líneas paralelas a las aristas que pasan por su punto simediano .

Si los lados sucesivos de un hexágono cíclico son a , b , c , d , e , f , entonces las tres diagonales principales se intersecan en un solo punto si y sólo si ace = bdf . ^[6]

Si, para cada lado de un hexágono cíclico, los lados adyacentes se extienden hasta su intersección, formando un triángulo exterior al lado dado, entonces los segmentos que conectan los circuncentros de triángulos opuestos son concurrentes . ^[7]

Si un hexágono tiene vértices en el círculo circunscrito de un triángulo agudo en los seis puntos (incluidos tres vértices del triángulo) donde las alturas extendidas del triángulo se encuentran con el círculo circunscrito, entonces el área del hexágono es el doble del área del triángulo. ^{[8] : p. 179}

Sea ABCDEF un hexágono formado por seis rectas tangentes a una sección cónica. Entonces el teorema de Brianchon establece que las tres diagonales principales AD, BE y CF se cortan en un único punto.

En un hexágono que es tangente a un círculo y que tiene lados consecutivos a , b , c , d , e y f , ^[9]

${\displaystyle a+c+e=b+d+f.}$

Si se construye un triángulo equilátero externamente en cada lado de cualquier hexágono, entonces los puntos medios de los segmentos que conectan los centroides de triángulos opuestos forman otro triángulo equilátero. ^{[10] : Teo. 1}

Un hexágono oblicuo es un polígono oblicuo con seis vértices y aristas pero que no se encuentran en el mismo plano. El interior de un hexágono de este tipo no suele estar definido. Un hexágono oblicuo en zigzag tiene vértices que se alternan entre dos planos paralelos.

Un hexágono oblicuo regular es transitivo por vértices con longitudes de aristas iguales. En tres dimensiones será un hexágono oblicuo en zigzag y se puede ver en los vértices y aristas laterales de un antiprisma triangular con la misma simetría D _3d , [2 ⁺ ,6], orden 12.

El cubo y el octaedro (igual que el antiprisma triangular) tienen hexágonos oblicuos regulares como polígonos de Petrie.

Hexágonos oblicuos en ejes triples

Cubo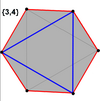

Octaedro

El hexágono oblicuo regular es el polígono de Petrie para estos poliedros y politopos regulares , uniformes y duales de dimensiones superiores, que se muestran en estas proyecciones ortogonales oblicuas :

4D		5D
Duoprisma 3-3	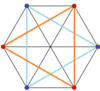3-3 duopirámide	5-símplex

La diagonal principal de un hexágono es la diagonal que divide al hexágono en cuadriláteros. En cualquier hexágono equilátero convexo (uno con todos los lados iguales) con un lado común a , existe ^{[11] : p.184, #286.3} una diagonal principal d ₁ tal que

${\displaystyle {\frac {d_{1}}{a}}\leq 2}$

y una diagonal principal d ₂ tal que

${\displaystyle {\frac {d_{2}}{a}}>{\sqrt {3}}.}$

No existe un sólido platónico formado únicamente por hexágonos regulares, porque los hexágonos se teselan , lo que no permite que el resultado se "pliegue". Los sólidos arquimedianos con algunas caras hexagonales son el tetraedro truncado , el octaedro truncado , el icosaedro truncado (de la fama del balón de fútbol y el fulereno ), el cuboctaedro truncado y el icosidodecaedro truncado . Estos hexágonos pueden considerarse triángulos truncados , con diagramas de Coxeter de la formay.

Hexágonos en sólidos arquimedianos
Tetraédrico	Octaédrico		Icosaédrica
tetraedro truncado	octaedro truncado	cuboctaedro truncado	icosaedro truncado	icosidodecaedro truncado

Existen otros poliedros de simetría con hexágonos estirados o aplanados, como este poliedro de Goldberg G(2,0):

Hexágonos en los poliedros de Goldberg
Tetraédrico	Octaédrico	Icosaédrica
Tetraedro biselado	Cubo biselado	Dodecaedro biselado

También hay 9 sólidos de Johnson con hexágonos regulares:

Sólidos de Johnson con hexágonos
cúpula triangular	cúpula triangular alargada	Cúpula triangular giroelongada
prisma hexagonal aumentado	prisma hexagonal parabiaumentado	prisma hexagonal metabiaumentado
prisma hexagonal triaumentado	tetraedro truncado aumentado	Hebesfenorrotunda triangular

Prismoides con hexágonos
Prisma hexagonal	Antiprisma hexagonal	Pirámide hexagonal

Azulejos con hexágonos regulares
Regular	1-uniform
{6,3}	r{6,3}	rr{6,3}	tr{6,3}
2-azulejos uniformes

• 
  La estructura cristalina ideal del grafeno es una rejilla hexagonal.
• 
  Segmentos de espejo E-ELT ensamblados
• 
  Un panal de abejas
• 
  Los escudos del caparazón de una tortuga
• 
  El hexágono de Saturno , un patrón de nubes hexagonal alrededor del polo norte del planeta.
• 
  Micrografía de un copo de nieve
• 
  Benceno , el compuesto aromático más simple con forma hexagonal.
• 
  Orden hexagonal de burbujas en una espuma.
• 
  Estructura cristalina de un hexágono molecular compuesto por anillos aromáticos hexagonales.
• 
  Columnas de basalto formadas naturalmente en la Calzada del Gigante en Irlanda del Norte ; las grandes masas deben enfriarse lentamente para formar un patrón de fractura poligonal
• 
  Vista aérea del Fuerte Jefferson en el Parque Nacional Dry Tortugas
• 
  El espejo del telescopio espacial James Webb está compuesto por 18 segmentos hexagonales.
• 
  En francés, l'Hexagone se refiere a la Francia metropolitana por su forma vagamente hexagonal.
• 
  Cristal de hanksita hexagonal , uno de los muchos minerales del sistema cristalino hexagonal
• 
  Granero hexagonal
• 
  The Hexagon , un teatro hexagonal en Reading, Berkshire
• 
  El ajedrez hexagonal de Władysław Gliński
• 
  Pabellón en el Jardín Botánico de Taiwán
• 
  Ventana hexagonal

• 24 celdas : una figura de cuatro dimensiones que, como el hexágono, tiene facetas ortoplexas , es autodual y tesela el espacio euclidiano.
• Sistema cristalino hexagonal
• Número hexagonal
• Mosaico hexagonal : mosaico regular de hexágonos en un plano.
• Hexagrama : estrella de seis lados dentro de un hexágono regular
• Hexagrama unicursal : camino único, estrella de seis lados, dentro de un hexágono
• Conjetura del panal
• Havannah : juego de mesa abstracto que se juega en una cuadrícula hexagonal de seis lados.
• Teoría del lugar central

Busque hexágono en Wikcionario, el diccionario libre.

• Weisstein, Eric W. "Hexágono". MathWorld .

• Definición y propiedades de un hexágono con animación interactiva y construcción con compás y regla.
• Una introducción a la geometría hexagonal en Hexnet, un sitio web dedicado a las matemáticas hexagonales.
• Los hexágonos son los mejores en YouTube : un video animado de Internet sobre hexágonos realizado por CGP Grey .