Grupo cíclico

Estructura algebraica → Teoría de grupos Teoría de grupos
Nociones básicas Subgrupo Subgrupo normal Acción grupal Grupo de cocientes Producto (semi) directo Suma directa Producto gratuito Producto de corona Homomorfismos de grupo núcleo imagen simple finito infinito continuo multiplicativo aditivo cíclico abeliano diedro nilpotente soluble Glosario de teoría de grupos Lista de temas de teoría de grupos
Grupos finitos Grupo cíclico Z n Grupo simétrico S n Grupo alterno A n Grupo diedro D n Grupo de cuaterniones Q Teorema de Cauchy Teorema de Lagrange Teoremas de Sylow Teorema de Hall p -grupo Grupo abeliano elemental Grupo Frobenius Multiplicador de Schur Clasificación de grupos finitos simples cíclico alterno Tipo de mentira esporádico
Grupos discretos Celosías Números enteros (${\displaystyle \mathbb {Z}}$) Grupo libre Grupos modulares LPS(2,${\displaystyle \mathbb {Z}}$) SL(2,${\displaystyle \mathbb {Z}}$) Grupo aritmético Enrejado Grupo hiperbólico
Grupos topológicos y de Lie Solenoide Círculo GL lineal general ( n ) SL lineal especial ( n ) O( n ) ortogonal E( n ) euclidiana SO( n ) ortogonal especial Unitario U( n ) SU unitario especial ( n ) Sp( n ) simpléctico G2​ F4​ E6​ E7​ E8​ Lorentz Poincaré Conforme Difeomorfismo Bucle Grupo de Lie de dimensión infinita O(∞) SU(∞) Sp(∞)
Grupos algebraicos Grupo algebraico lineal Grupo reductivo Variedad abeliana Curva elíptica
en a mi

En álgebra abstracta , un grupo cíclico o grupo monógeno es un grupo , denotado C _n (también frecuentemente _n o Z _n , que no debe confundirse con el anillo conmutativo de números p -ádicos ), que es generado por un solo elemento. ^[1] Es decir, es un conjunto de elementos invertibles con una sola operación binaria asociativa , y contiene un elemento  g tal que cada otro elemento del grupo puede obtenerse aplicando repetidamente la operación de grupo a  g o su inversa. Cada elemento puede escribirse como una potencia entera de  g en notación multiplicativa, o como un múltiplo entero de g en notación aditiva. Este elemento  g se llama generador del grupo. ^[1]${\displaystyle \mathbb {Z} }$

Todo grupo cíclico infinito es isomorfo al grupo aditivo de  Z , los números enteros . Todo grupo cíclico finito de orden  n es isomorfo al grupo aditivo de Z / n Z , los números enteros módulo  n . Todo grupo cíclico es un grupo abeliano (lo que significa que su operación de grupo es conmutativa ), y todo grupo abeliano finitamente generado es un producto directo de grupos cíclicos.

Todo grupo cíclico de orden primo es un grupo simple , que no puede descomponerse en grupos más pequeños. En la clasificación de los grupos simples finitos , una de las tres clases infinitas está formada por los grupos cíclicos de orden primo. Los grupos cíclicos de orden primo se encuentran, por tanto, entre los bloques a partir de los cuales pueden construirse todos los grupos.

Para cualquier elemento  g en cualquier grupo  G , se puede formar el subgrupo que consiste en todas sus potencias enteras: ⟨ g ⟩ = { g ^k | k ∈ Z } , llamado el subgrupo cíclico generado por  g . El orden de  g es |⟨ g ⟩|, el número de elementos en ⟨ g ⟩, abreviado convencionalmente como | g |, como ord( g ), o como o( g ). Es decir, el orden de un elemento es igual al orden del subgrupo cíclico que genera.

Un grupo cíclico es un grupo que es igual a uno de sus subgrupos cíclicos: G = ⟨ g ⟩ para algún elemento  g , llamado generador de G .

Para un grupo cíclico finito  G de orden  n tenemos G = { e , g , g ² , ... , g ^{n −1} } , donde e es el elemento identidad y g ⁱ = g ^j siempre que i ≡ j ( mod  n ); en particular g ⁿ = g ⁰ = e , y g ⁻¹ = g ^{n −1} . Un grupo abstracto definido por esta multiplicación a menudo se denota C _n , y decimos que G es isomorfo al grupo cíclico estándar C _n . Un grupo así también es isomorfo a Z / n Z , el grupo de números enteros módulo n con la operación de adición, que es el grupo cíclico estándar en notación aditiva. Bajo el isomorfismo χ definido por χ ( g ⁱ ) = i el elemento identidad  e corresponde a 0, los productos corresponden a las sumas y las potencias corresponden a los múltiplos.

Por ejemplo, el conjunto de raíces 6tas complejas de la unidad: forma un grupo bajo multiplicación. Es cíclico, ya que es generado por la raíz primitiva que es, G = ⟨ z ⟩ = { 1, z , z ² , z ³ , z ⁴ , z ⁵ } con z ⁶ = 1. Bajo un cambio de letras, esto es isomorfo a (estructuralmente igual que) el grupo cíclico estándar de orden 6, definido como C ₆ = ⟨ g ⟩ = { e , g , g ² , g ³ , g ⁴ , g ⁵ } con multiplicación g ^j · g ^k = g ^{j + k (mod 6)} , de modo que g ⁶ = g ⁰ = e . Estos grupos también son isomorfos a Z /6 Z = {0, 1, 2, 3, 4, 5} con la operación de adición módulo 6, correspondiendo z ^k y g ^k a  k . Por ejemplo, 1 + 2 ≡ 3 (mod 6) corresponde a z ¹ · z ² = z ³ , y 2 + 5 ≡ 1 (mod 6) corresponde a z ² · z ⁵ = z ⁷ = z ¹ , y así sucesivamente. Cualquier elemento genera su propio subgrupo cíclico, como ⟨ z ² ⟩ = { e , z ² , z ⁴ } de orden 3, isomorfo a C ₃ y Z /3 Z ; y ⟨ z ⁵ ⟩ = { e , z ⁵ , z ¹⁰ = z ⁴ , z ¹⁵ = z ³ , z ²⁰ = z ² , z ²⁵ = z } = G , de modo que z ⁵ tiene orden 6 y es un generador alternativo de  G$${\displaystyle G=\left\{\pm 1,\pm {\left({\tfrac {1}{2}}+{\tfrac {\sqrt {3}}{2}}i\right)},\pm {\left({\tfrac {1}{2}}-{\tfrac {\sqrt {3}}{2}}i\right)}\right\}}$$ ${\displaystyle z={\tfrac {1}{2}}+{\tfrac {\sqrt {3}}{2}}i=e^{2\pi i/6}:}$ .

En lugar de las notaciones de cociente Z / n Z , Z /( n ) o Z / n , algunos autores denotan un grupo cíclico finito como Z _n , pero esto choca con la notación de la teoría de números , donde Z _p denota un anillo de números p -ádico , o localización en un ideal primo .

Grupos cíclicos infinitos

p1, ( *∞∞ )	pág. 11g, (22∞)
Dos grupos de frisos son isomorfos a  Z. Con un generador, p1 tiene traslaciones y p11g tiene reflexiones de deslizamiento.

Por otra parte, en un grupo cíclico infinito G = ⟨ g ⟩ , las potencias g ^k dan elementos distintos para todos los enteros k , de modo que G = { ... , g ⁻² , g ⁻¹ , e , g , g ² , ... }, y G es isomorfo al grupo estándar C = C _∞ y a Z , el grupo aditivo de los enteros. Un ejemplo es el primer grupo de friso . Aquí no hay ciclos finitos, y el nombre "cíclico" puede ser engañoso. ^[2]

Para evitar esta confusión, Bourbaki introdujo el término grupo monógeno para un grupo con un único generador y restringió el término "grupo cíclico" para significar un grupo monógeno finito, evitando el término "grupo cíclico infinito". ^{[nota 1]}

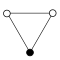
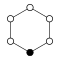
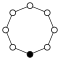
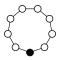
Ejemplos de grupos cíclicos en simetría rotacional

C 1	C 2	C 3
C 4	C 5	C6

El conjunto de números enteros  Z , con la operación de adición, forma un grupo. ^[1] Es un grupo cíclico infinito , porque todos los números enteros pueden escribirse sumando o restando repetidamente el único número 1. En este grupo, 1 y −1 son los únicos generadores. Todo grupo cíclico infinito es isomorfo a  Z .

Para cada entero positivo  n , el conjunto de enteros módulo  n , de nuevo con la operación de adición, forma un grupo cíclico finito, denotado Z / n Z . ^[1] Un entero modular  i es un generador de este grupo si i es relativamente primo a  n , porque estos elementos pueden generar todos los demás elementos del grupo a través de la adición de enteros. (El número de tales generadores es φ ( n ), donde φ es la función totient de Euler .) Todo grupo cíclico finito G es isomorfo a Z / n Z , donde n = | G | es el orden del grupo.

Las operaciones de adición de números enteros y enteros modulares, utilizadas para definir los grupos cíclicos, son las operaciones de adición de anillos conmutativos , también denotadas Z y Z / n Z o Z / ( n ). Si p es un primo , entonces Z / p Z es un cuerpo finito , y usualmente se denota F _p o GF ( p ) para el cuerpo de Galois.

Para cada entero positivo  n , el conjunto de los enteros módulo  n que son primos entre sí con  n se escribe como ( Z / n Z ) ^× ; forma un grupo bajo la operación de multiplicación. Este grupo no siempre es cíclico, pero lo es siempre que n sea 1, 2, 4, una potencia de un primo impar o el doble de una potencia de un primo impar (secuencia A033948 en la OEIS ). ^{[4] [5]} Este es el grupo multiplicativo de unidades del anillo Z / n Z ; hay φ ( n ) de ellas, donde nuevamente φ es la función totient de Euler . Por ejemplo, ( Z /6 Z ) ^× = {1, 5}, y dado que 6 es el doble de un primo impar, este es un grupo cíclico. En contraste, ( Z /8 Z ) ^× = {1, 3, 5, 7} es un 4-grupo de Klein y no es cíclico. Cuando ( Z / n Z ) ^× es cíclico, sus generadores se llaman raíces primitivas módulo n .

Para un número primo  p , el grupo ( Z / p Z ) ^× es siempre cíclico, y está formado por los elementos no nulos del cuerpo finito de orden  p . En términos más generales, todo subgrupo finito del grupo multiplicativo de cualquier cuerpo es cíclico. ^[6]

El conjunto de simetrías rotacionales de un polígono forma un grupo cíclico finito. ^[7] Si hay n maneras diferentes de mover el polígono hacia sí mismo mediante una rotación (incluyendo la rotación nula) entonces este grupo de simetría es isomorfo a Z / n Z . En tres dimensiones o más existen otros grupos de simetría finitos que son cíclicos , pero que no son todas rotaciones alrededor de un eje, sino rotoreflexiones .

El grupo de todas las rotaciones de un círculo (el grupo del círculo , también denominado S ^{1 )} no es cíclico, porque no existe una única rotación cuyas potencias enteras generen todas las rotaciones. De hecho, el grupo cíclico infinito C _∞ es contable , mientras que S ¹ no lo es. El grupo de rotaciones por ángulos racionales es contable, pero aún así no es cíclico.

Una raíz n -ésima de la unidad es un número complejo cuya potencia n -ésima es 1, una raíz del polinomio x ⁿ − 1 . El conjunto de todas las raíces n -ésimas de la unidad forma un grupo cíclico de orden n bajo la multiplicación. ^[1] Los generadores de este grupo cíclico son las raíces primitivas n -ésimas de la unidad ; son las raíces del polinomio ciclotómico n -ésimo . Por ejemplo, el polinomio z ³ − 1 se factoriza como ( z − 1)( z − ω )( z − ω ² ) , donde ω = e ^{2 πi /3} ; el conjunto {1, ω , ω ² } = { ω ⁰ , ω ¹ , ω ² } forma un grupo cíclico bajo la multiplicación. El grupo de Galois de la extensión del campo de los números racionales generados por las raíces n -ésimas de la unidad forma un grupo diferente, isomorfo al grupo multiplicativo ( Z/ n Z ) ^× de orden φ ( n ) , que es cíclico para algunos pero no para todos  los n (ver arriba).

Una extensión de campo se denomina extensión cíclica si su grupo de Galois es cíclico. Para campos de característica cero , tales extensiones son objeto de la teoría de Kummer y están íntimamente relacionadas con la solubilidad por radicales . Para una extensión de campos finitos de característica  p , su grupo de Galois es siempre finito y cíclico, generado por una potencia de la función de Frobenius . ^[8] A la inversa, dado un campo finito  F y un grupo cíclico finito  G , existe una extensión de campo finito de  F cuyo grupo de Galois es  G. ^[9 ]

Todos los subgrupos y grupos cocientes de grupos cíclicos son cíclicos. Específicamente, todos los subgrupos de Z son de la forma ⟨ m ⟩ = m Z , con m un entero positivo. Todos estos subgrupos son distintos entre sí, y aparte del grupo trivial {0} = 0 Z , todos son isomorfos a  Z . La red de subgrupos de Z es isomorfa al dual de la red de números naturales ordenados por divisibilidad . ^[10] Por lo tanto, dado que un número primo  p no tiene divisores no triviales, p Z es un subgrupo propio maximal, y el grupo cociente Z / p Z es simple ; de hecho, un grupo cíclico es simple si y solo si su orden es primo. ^[11]

Todos los grupos cocientes Z / n Z son finitos, con excepción de Z /0 Z = Z /{0}. Para cada divisor positivo  d de  n , el grupo cociente Z / n Z tiene precisamente un subgrupo de orden  d , generado por la clase de residuo de  n / d . No hay otros subgrupos.

Todo grupo cíclico es abeliano . ^[1] Es decir, su operación de grupo es conmutativa : gh = hg (para todo g y h en G ). Esto es claro para los grupos de adición entera y modular ya que r + s ≡ s + r (mod n ) y se deduce para todos los grupos cíclicos ya que todos son isomorfos a estos grupos estándar. Para un grupo cíclico finito de orden n , g ⁿ es el elemento identidad para cualquier elemento  g . Esto nuevamente se deduce usando el isomorfismo a la adición modular, ya que kn ≡ 0 (mod n ) para cada entero  k . (Esto también es cierto para un grupo general de orden n , debido al teorema de Lagrange ).

En el caso de una potencia prima , el grupo se denomina grupo cíclico primario . El teorema fundamental de los grupos abelianos establece que todo grupo abeliano finitamente generado es un producto directo finito de grupos cíclicos primarios y grupos cíclicos infinitos.${\displaystyle p^{k}}$${\displaystyle Z/p^{k}Z}$

Como un grupo cíclico es abeliano, cada una de sus clases de conjugación consta de un único elemento. Por lo tanto, un grupo cíclico de orden  n tiene n clases de conjugación.

Si d es divisor de  n , entonces el número de elementos en Z / n Z que tienen orden d es φ ( d ), y el número de elementos cuyo orden divide a d es exactamente  d . Si G es un grupo finito en el que, para cada n > 0 , G contiene como máximo n elementos de orden que divide a n , entonces G debe ser cíclico. ^{[nota 2]} El orden de un elemento m en Z / n Z es n / mcd ( n , m ).

Si n y m son coprimos , entonces el producto directo de dos grupos cíclicos Z / n Z y Z / m Z es isomorfo al grupo cíclico Z / nm Z , y también se cumple la inversa: esta es una forma del teorema del resto chino . Por ejemplo, Z /12 Z es isomorfo al producto directo Z /3 Z × Z /4 Z bajo el isomorfismo ( k mod 12) → ( k mod 3, k mod 4) ; pero no es isomorfo a Z /6 Z × Z /2 Z , en el que cada elemento tiene orden como máximo 6.

Si p es un número primo , entonces cualquier grupo con p elementos es isomorfo al grupo simple Z / p Z . Un número n se llama número cíclico si Z / n Z es el único grupo de orden  n , lo cual es cierto exactamente cuando mcd( n , φ ( n )) = 1 . ^[13] La secuencia de números cíclicos incluye todos los primos, pero algunos son compuestos como 15. Sin embargo, todos los números cíclicos son impares excepto 2. Los números cíclicos son:

1, 2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 41, 43, 47, 51, 53, 59, 61, 65, 67, 69, 71, 73, 77, 79, 83, 85, 87, 89, 91, 95, 97, 101, 103, 107, 109, 113, 115, 119, 123, 127, 131, 133, 137, 139, 141, 143, ... (secuencia A003277 en la OEIS )

La definición implica inmediatamente que los grupos cíclicos tienen presentación de grupo C _∞ = ⟨ x | ⟩ y C _n = ⟨ x | x ⁿ ⟩ para n finito  . ^[14]

La teoría de la representación del grupo cíclico es un caso base crítico para la teoría de la representación de grupos finitos más generales. En el caso complejo , una representación de un grupo cíclico se descompone en una suma directa de caracteres lineales, haciendo transparente la conexión entre la teoría de caracteres y la teoría de la representación. En el caso característico positivo , las representaciones indecomponibles del grupo cíclico forman un modelo y una base inductiva para la teoría de la representación de grupos con subgrupos de Sylow cíclicos y, de manera más general, la teoría de la representación de bloques de defecto cíclico.

Un gráfico de ciclo ilustra los diversos ciclos de un grupo y es particularmente útil para visualizar la estructura de pequeños grupos finitos . Un gráfico de ciclo para un grupo cíclico es simplemente un gráfico circular , donde el orden del grupo es igual al número de nodos. Un generador único define el grupo como una ruta direccional en el gráfico, y el generador inverso define una ruta hacia atrás. Una ruta trivial (identidad) se puede dibujar como un bucle , pero generalmente se suprime. Z ₂ a veces se dibuja con dos bordes curvos como un multigrafo . ^[15]

Un grupo cíclico Z _n , con orden n , corresponde a un ciclo único graficado simplemente como un polígono de n lados con los elementos en los vértices.

Gráficas de ciclos hasta orden 24

El 1	El 2	El 3	Z4​	Z5​	Z6 = Z3 × Z2​	Z7​	Z8​
Z9​	Z10 = Z5 × Z2​	El 11	Z12 = Z4 × Z3​	El 13	Z14 = Z7 × Z2​	Z15 = Z5 × Z3​	Z16​
El 17	Z18 = Z9 × Z2​	El 19	Z20 = Z5 × Z4​	Z21 = Z7 × Z3​	Z22 = Z11 × Z2​	Z23​	Z24 = Z8 × Z3​

Un grafo de Cayley es un grafo definido a partir de un par ( G , S ) donde G es un grupo y S es un conjunto de generadores para el grupo; tiene un vértice para cada elemento del grupo y una arista para cada producto de un elemento con un generador. En el caso de un grupo cíclico finito, con su único generador, el grafo de Cayley es un grafo de ciclo , y para un grupo cíclico infinito con su generador, el grafo de Cayley es un grafo de trayectoria doblemente infinito . Sin embargo, los grafos de Cayley también se pueden definir a partir de otros conjuntos de generadores. Los grafos de Cayley de grupos cíclicos con conjuntos generadores arbitrarios se denominan grafos circulantes . ^[16] Estos grafos se pueden representar geométricamente como un conjunto de puntos igualmente espaciados en un círculo o en una línea, con cada punto conectado a vecinos con el mismo conjunto de distancias que cada otro punto. Son exactamente los grafos transitivos de vértice cuyo grupo de simetría incluye un grupo cíclico transitivo. ^[17]

El anillo de endomorfismo del grupo abeliano Z/nZ es isomorfo al propio Z/nZ como anillo. [18] Bajo este isomorfismo, el número r corresponde al endomorfismo de Z/nZ que asigna cada elemento a la suma de r copias del mismo ^. Esto es una biyección si y solo si r es coprimo con n , por lo que el grupo de automorfismo de Z / nZ es isomorfo al grupo unitario ( Z / nZ ) ^× . ^[18]

De manera similar, el anillo de endomorfismo del grupo aditivo de  Z es isomorfo al anillo  Z . Su grupo de automorfismo es isomorfo al grupo de unidades del anillo  Z , que es ({−1, +1}, ×) ≅ C ₂ .

Se puede demostrar que el producto tensorial Z / m Z ⊗ Z / n Z es isomorfo a Z / mcd( m , n ) Z . De modo que podemos formar la colección de homomorfismos de grupo desde Z / m Z hasta Z / n Z , denotada hom( Z / m Z , Z / n Z ) , que es en sí misma un grupo.

Para el producto tensorial, esto es una consecuencia del hecho general de que R / I ⊗ _R R / J ≅ R /( I + J ) , donde R es un anillo conmutativo con unidad e I y J son ideales del anillo. Para el grupo Hom, recuerde que es isomorfo al subgrupo de Z / n Z que consiste en los elementos de orden que dividen a m . Ese subgrupo es cíclico de orden mcd( m , n ) , lo que completa la prueba.

Se han definido varias otras clases de grupos por su relación con los grupos cíclicos:

Un grupo se llama virtualmente cíclico si contiene un subgrupo cíclico de índice finito (el número de clases laterales que tiene el subgrupo). En otras palabras, cualquier elemento en un grupo virtualmente cíclico se puede obtener multiplicando un miembro del subgrupo cíclico y un miembro de un cierto conjunto finito. Todo grupo cíclico es virtualmente cíclico, como lo es todo grupo finito. Un grupo infinito es virtualmente cíclico si y solo si es finitamente generado y tiene exactamente dos extremos ; ^{[nota 3]} un ejemplo de tal grupo es el producto directo de Z / n Z y Z , en el que el factor Z tiene índice finito  n . Todo subgrupo abeliano de un grupo hiperbólico de Gromov es virtualmente cíclico. ^[20]

Un grupo profinito se denomina procíclico si puede generarse topológicamente a partir de un único elemento. Entre los ejemplos de grupos profinitos se incluyen los números enteros profinitos o los números enteros p -ádicos para un número primo p .${\displaystyle {\widehat {\mathbb {Z} }}}$${\displaystyle \mathbb {Z} _{p}}$

Un grupo localmente cíclico es un grupo en el que cada subgrupo finitamente generado es cíclico. Un ejemplo es el grupo aditivo de los números racionales : cada conjunto finito de números racionales es un conjunto de múltiplos enteros de una única fracción unitaria , el inverso de su mínimo común denominador , y genera como subgrupo un grupo cíclico de múltiplos enteros de esta fracción unitaria. Un grupo es localmente cíclico si y solo si su red de subgrupos es una red distributiva . ^[21]

Un grupo ordenado cíclicamente es un grupo que conserva un orden cíclico gracias a la estructura del grupo. A cada grupo cíclico se le puede dar una estructura como grupo ordenado cíclicamente, de acuerdo con el orden de los números enteros (o de los números enteros módulo el orden del grupo). Cada subgrupo finito de un grupo ordenado cíclicamente es cíclico. ^[22]

Un grupo metacíclico es un grupo que contiene un subgrupo normal cíclico cuyo cociente también es cíclico. ^[23] Estos grupos incluyen los grupos cíclicos, los grupos dicíclicos y los productos directos de dos grupos cíclicos. Los grupos policíclicos generalizan los grupos metacíclicos al permitir más de un nivel de extensión de grupo . Un grupo es policíclico si tiene una secuencia descendente finita de subgrupos, cada uno de los cuales es normal en el subgrupo anterior con un cociente cíclico, que termina en el grupo trivial. Todo grupo abeliano o grupo nilpotente finitamente generado es policíclico. ^[24]

• Gráfica de ciclo (grupo)
• Módulo cíclico
• Tamizado cíclico
• Grupo de Prüfer ( análogo numerable infinito )
• Grupo circular ( análogo infinito incontable )

• Alonso, JM; et al. (1991), "Notes on word hyperbolic groups", Teoría de grupos desde un punto de vista geométrico (Trieste, 1990) (PDF) , River Edge, NJ: World Scientific, Corolario 3.6, MR  1170363, archivado desde el original (PDF) el 25 de abril de 2013 , consultado el 26 de noviembre de 2013
• Alspach, Brian (1997), "Isomorfismo y grafos de Cayley en grupos abelianos", Graph symmetry (Montreal, PQ, 1996), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 497, Dordrecht: Kluwer Acad. Publ., págs. 1–22, ISBN 978-0-792-34668-5, Sr.  1468786
• Aluffi, Paolo (2009), "6.4 Ejemplo: subgrupos de grupos cíclicos", Álgebra, Capítulo 0, Estudios de posgrado en matemáticas , vol. 104, American Mathematical Society, págs. 82–84, ISBN 978-0-8218-4781-7
• Bourbaki, Nicolas (1998-08-03) [1970], Álgebra I: Capítulos 1-3, Elementos de Matemáticas, vol. 1 (edición reimpresa en tapa blanda), Springer Science & Business Media, ISBN 978-3-540-64243-5
• Coxeter, HSM ; Moser, WOJ (1980), Generadores y relaciones para grupos discretos , Nueva York: Springer-Verlag, p. 1, ISBN 0-387-09212-9
• Lajoie, Caroline; Mura, Roberta (noviembre de 2000), "¿Qué hay en un nombre? Una dificultad de aprendizaje relacionada con los grupos cíclicos", For the Learning of Mathematics , 20 (3): 29–33, JSTOR  40248334
• Cox, David A. (2012), Teoría de Galois , Matemáticas puras y aplicadas (2.ª ed.), John Wiley & Sons, Teorema 11.1.7, pág. 294, doi : 10.1002/9781118218457, ISBN 978-1-118-07205-9
• Gallian, Joseph (2010), Álgebra abstracta contemporánea (7.ª ed.), Cengage Learning, Ejercicio 43, pág. 84, ISBN 978-0-547-16509-7
• Gannon, Terry (2006), Moonshine más allá del monstruo: el puente que conecta el álgebra, las formas modulares y la física, Monografías de Cambridge sobre física matemática, Cambridge University Press, pág. 18, ISBN 978-0-521-83531-2, Z _n es simple si y solo si n es primo.
• Jungnickel, Dieter (1992), "Sobre la unicidad del grupo cíclico de orden n ", American Mathematical Monthly , 99 (6): 545–547, doi :10.2307/2324062, JSTOR  2324062, MR  1166004
• Fuchs, László (2011), Sistemas algebraicos parcialmente ordenados, Serie internacional de monografías sobre matemáticas puras y aplicadas, vol. 28, Courier Dover Publications, pág. 63, ISBN 978-0-486-48387-0
• Kurzweil, Hans; Stellmacher, Bernd (2004), La teoría de los grupos finitos: una introducción, Universitext, Springer, pág. 50, ISBN 978-0-387-40510-0
• Motwani, Rajeev ; Raghavan, Prabhakar (1995), Algoritmos aleatorios, Cambridge University Press, Teorema 14.14, pág. 401, ISBN 978-0-521-47465-8
• Ore, Øystein (1938), "Estructuras y teoría de grupos. II", Duke Mathematical Journal , 4 (2): 247–269, doi :10.1215/S0012-7094-38-00419-3, hdl : 10338.dmlcz/100155 , MR  1546048
• Rotman, Joseph J. (1998), Teoría de Galois, Universitext, Springer, Teorema 62, pág. 65, ISBN 978-0-387-98541-1
• Stallings, John (1970), "Grupos de dimensión cohomológica uno", Aplicaciones del álgebra categórica (Proc. Sympos. Pure Math., vol. XVIII, Nueva York, 1968) , Providence, RI: Amer. Math. Soc., págs. 124-128, MR  0255689
• Stewart, Ian ; Golubitsky, Martin (2010), Simetría temible: ¿es Dios un geómetra?, Courier Dover Publications, págs. 47–48, ISBN 978-0-486-47758-9
• Vilfred, V. (2004), "Sobre los grafos circulantes", en Balakrishnan, R.; Sethuraman, G.; Wilson, Robin J. (eds.), Graph Theory and its Applications (Anna University, Chennai, 14-16 de marzo de 2001), Alpha Science, págs. 34-36, ISBN 8173195692
• Vinogradov, IM (2003), "§ VI RAÍCES E ÍNDICES PRIMITIVOS", Elementos de teoría de números , Mineola, NY: Dover Publications, págs. 105-132, ISBN 0-486-49530-2

• Herstein, IN (1996), Álgebra abstracta (3.ª ed.), Prentice Hall , págs. 53–60, ISBN 978-0-13-374562-7, Sr.  1375019

• Milne, Teoría de grupos, http://www.jmilne.org/math/CourseNotes/gt.html
• Introducción a los grupos cíclicos
• Weisstein, Eric W. "Grupo cíclico". MathWorld .
• Grupos cíclicos de orden pequeño en GroupNames
• Todo grupo cíclico es abeliano