Distribución beta
Función de densidad de probabilidad  | |||
Función de distribución acumulativa 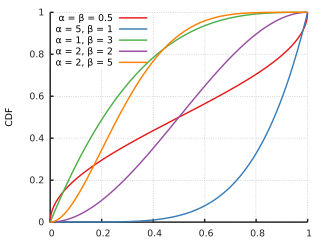 | |||
| Notación | Beta( α , β ) | ||
|---|---|---|---|
| Parámetros | α > 0 forma ( real ) β > 0 forma ( real ) | ||
| Apoyo | o | ||
donde y es la función Gamma . | |||
| CDF | (la función beta incompleta regularizada ) | ||
| Significar |
| ||
| Mediana | |||
| Modo | para α , β > 1 cualquier valor en para α , β = 1 {0, 1} (bimodal) para α , β < 1 0 para α ≤ 1, β ≥ 1, α ≠ β 1 para α ≥ 1, β ≤ 1, α ≠ β | ||
| Diferencia | (ver función trigamma y ver sección: Varianza geométrica) | ||
| Oblicuidad | |||
| Exceso de curtosis | |||
| Entropía | |||
| MGF | |||
| CF | (ver Función hipergeométrica confluente ) | ||
| Información de Fisher | Ver sección: Matriz de información de Fisher | ||
| Método de momentos | |||
En teoría de probabilidad y estadística , la distribución beta es una familia de distribuciones de probabilidad continuas definidas en el intervalo [0, 1] o (0, 1) en términos de dos parámetros positivos , denotados por alfa ( α ) y beta ( β ), que aparecen como exponentes de la variable y su complemento a 1, respectivamente, y controlan la forma de la distribución.
La distribución beta se ha aplicado para modelar el comportamiento de variables aleatorias limitadas a intervalos de longitud finita en una amplia variedad de disciplinas. La distribución beta es un modelo adecuado para el comportamiento aleatorio de porcentajes y proporciones.
En la inferencia bayesiana , la distribución beta es la distribución de probabilidad previa conjugada para las distribuciones de Bernoulli , binomial , binomial negativa y geométrica .
La formulación de la distribución beta que se analiza aquí también se conoce como distribución beta de primer tipo , mientras que la distribución beta de segundo tipo es un nombre alternativo para la distribución beta prima . La generalización a múltiples variables se denomina distribución de Dirichlet .
Definiciones
Función de densidad de probabilidad

La función de densidad de probabilidad (PDF) de la distribución beta, para o , y parámetros de forma , , es una función de potencia de la variable y de su reflejo como sigue:
donde es la función gamma . La función beta , , es una constante de normalización para garantizar que la probabilidad total sea 1. En las ecuaciones anteriores hay una realización —un valor observado que realmente ocurrió— de una variable aleatoria .
Varios autores, incluidos NL Johnson y S. Kotz , [1] utilizan los símbolos y (en lugar de y ) para los parámetros de forma de la distribución beta, que recuerdan a los símbolos utilizados tradicionalmente para los parámetros de la distribución de Bernoulli , porque la distribución beta se aproxima a la distribución de Bernoulli en el límite cuando ambos parámetros de forma y se aproximan al valor de cero.
A continuación, se presenta una variable aleatoria con distribución beta y parámetros y que se denotará por: [2] [3]
Otras notaciones para variables aleatorias distribuidas en beta utilizadas en la literatura estadística son [4] y [5] .
Función de distribución acumulativa


La función de distribución acumulativa es
donde es la función beta incompleta y es la función beta incompleta regularizada .
Parametrizaciones alternativas
Dos parámetros
Media y tamaño de la muestra
La distribución beta también puede ser reparametrizada en términos de su media μ (0 < μ < 1) y la suma de los dos parámetros de forma ν = α + β > 0 ( [3] p. 83). Denotando por αPosterior y βPosterior los parámetros de forma de la distribución beta posterior resultante de aplicar el teorema de Bayes a una función de verosimilitud binomial y una probabilidad previa, la interpretación de la suma de ambos parámetros de forma como tamaño de muestra = ν = α ·Posterior + β ·Posterior solo es correcta para la probabilidad previa de Haldane Beta(0,0). Específicamente, para la previa de Bayes (uniforme) Beta(1,1) la interpretación correcta sería tamaño de muestra = α ·Posterior + β Posterior − 2, o ν = (tamaño de muestra) + 2. Para un tamaño de muestra mucho mayor que 2, la diferencia entre estas dos previas se vuelve insignificante. (Ver la sección Inferencia bayesiana para más detalles.) ν = α + β se conoce como el "tamaño de muestra" de una distribución beta, pero uno debe recordar que es, estrictamente hablando, el "tamaño de muestra" de una función de verosimilitud binomial solo cuando se utiliza una distribución previa Haldane Beta(0,0) en el teorema de Bayes.
Esta parametrización puede ser útil en la estimación de parámetros bayesianos. Por ejemplo, se puede administrar una prueba a un número de individuos. Si se supone que la puntuación de cada persona (0 ≤ θ ≤ 1) se extrae de una distribución beta a nivel de población, entonces una estadística importante es la media de esta distribución a nivel de población. Los parámetros de media y tamaño de muestra están relacionados con los parámetros de forma α y β a través de [3].
- α = μν , β = (1 − μ ) ν
Bajo esta parametrización , se puede colocar una probabilidad previa no informativa sobre la media y una probabilidad previa vaga (como una distribución exponencial o gamma ) sobre los reales positivos para el tamaño de la muestra, si son independientes y los datos y/o creencias previos lo justifican.
Modo y concentración
Las distribuciones beta cóncavas , que tienen , se pueden parametrizar en términos de moda y "concentración". La moda, , y la concentración, , se pueden utilizar para definir los parámetros de forma habituales de la siguiente manera: [6]
Para que la moda, , esté bien definida, necesitamos , o equivalentemente . Si en cambio definimos la concentración como , la condición se simplifica a y la densidad beta en y puede escribirse como:
donde escala directamente las estadísticas suficientes , y . Nótese también que en el límite, , la distribución se vuelve plana.
Media y varianza
Resolviendo el sistema de ecuaciones (acopladas) dado en las secciones anteriores como las ecuaciones para la media y la varianza de la distribución beta en términos de los parámetros originales α y β , se pueden expresar los parámetros α y β en términos de la media ( μ ) y la varianza (var):
Esta parametrización de la distribución beta puede llevar a una comprensión más intuitiva que la basada en los parámetros originales α y β . Por ejemplo, expresando la moda, la asimetría, el exceso de curtosis y la entropía diferencial en términos de la media y la varianza:
Cuatro parámetros
Una distribución beta con los dos parámetros de forma α y β se admite en el rango [0,1] o (0,1). Es posible alterar la ubicación y la escala de la distribución introduciendo dos parámetros adicionales que representan los valores mínimos, a , y máximos c ( c > a ), de la distribución, [1] mediante una transformación lineal que sustituye la variable adimensional x en términos de la nueva variable y (con soporte [ a , c ] o ( a , c )) y los parámetros a y c :
La función de densidad de probabilidad de la distribución beta de cuatro parámetros es igual a la distribución de dos parámetros, escalada por el rango ( c − a ), (de modo que el área total bajo la curva de densidad es igual a una probabilidad de uno), y con la variable "y" desplazada y escalada de la siguiente manera:
Que una variable aleatoria Y tenga una distribución beta con cuatro parámetros α, β, a y c se denotará por:
Algunas medidas de ubicación central se escalan (por ( c − a )) y se desplazan (por a ), de la siguiente manera:
Nota: la media geométrica y la media armónica no se pueden transformar mediante una transformación lineal como sí lo hacen la media, la mediana y la moda.
Los parámetros de forma de Y se pueden escribir en términos de su media y varianza como
Las medidas de dispersión estadística se escalan (no es necesario desplazarlas porque ya están centradas en la media) por el rango ( c − a ), linealmente para la desviación media y no linealmente para la varianza:
Dado que la asimetría y el exceso de curtosis son cantidades adimensionales (como momentos centrados en la media y normalizados por la desviación estándar ), son independientes de los parámetros a y c , y por lo tanto iguales a las expresiones dadas anteriormente en términos de X (con soporte [0,1] o (0,1)):
Propiedades
Medidas de tendencia central
Modo
La moda de una variable aleatoria distribuida beta X con α , β > 1 es el valor más probable de la distribución (correspondiente al pico en la PDF), y se da mediante la siguiente expresión: [1]
Cuando ambos parámetros son menores que uno ( α , β < 1), este es el antimodo: el punto más bajo de la curva de densidad de probabilidad. [7]
Si α = β , la expresión para la moda se simplifica a 1/2, lo que demuestra que para α = β > 1 la moda (o antimoda cuando α , β < 1 ), está en el centro de la distribución: es simétrica en esos casos. Consulte la sección Formas de este artículo para obtener una lista completa de casos de moda, para valores arbitrarios de α y β . Para varios de estos casos, el valor máximo de la función de densidad ocurre en uno o ambos extremos. En algunos casos, el valor (máximo) de la función de densidad que ocurre en el extremo es finito. Por ejemplo, en el caso de α = 2, β = 1 (o α = 1, β = 2), la función de densidad se convierte en una distribución de triángulo rectángulo que es finita en ambos extremos. En varios otros casos, hay una singularidad en un extremo, donde el valor de la función de densidad se acerca al infinito. Por ejemplo, en el caso α = β = 1/2, la distribución beta se simplifica para convertirse en la distribución arcoseno . Existe un debate entre los matemáticos sobre algunos de estos casos y sobre si los extremos ( x = 0 y x = 1) pueden llamarse modos o no. [8] [2]

- Si los extremos son parte del dominio de la función de densidad
- Si una singularidad puede alguna vez ser llamada un modo
- ¿Los casos con dos máximos deben llamarse bimodales?
Mediana

_for_Beta_distribution_versus_alpha_and_beta_from_0_to_2_-_J._Rodal.jpg/440px-(Mean_-_Median)_for_Beta_distribution_versus_alpha_and_beta_from_0_to_2_-_J._Rodal.jpg)
La mediana de la distribución beta es el único número real para el cual se obtiene la función beta incompleta regularizada . No existe una expresión general en forma cerrada para la mediana de la distribución beta para valores arbitrarios de α y β . A continuación se presentan expresiones en forma cerrada para valores particulares de los parámetros α y β : [ cita requerida ]
- Para casos simétricos α = β , mediana = 1/2.
- Para α = 1 y β > 0, mediana (este caso es la imagen especular de la distribución de la función de potencia [0,1])
- Para α > 0 y β = 1, mediana = (en este caso se trata de la distribución de la función de potencia [0,1] [8] )
- Para α = 3 y β = 2, la mediana = 0,6142724318676105..., la solución real de la ecuación cuártica 1 − 8 x 3 + 6 x 4 = 0, que se encuentra en [0,1].
- Para α = 2 y β = 3, mediana = 0,38572756813238945... = 1−mediana(Beta(3, 2))
Los siguientes son los límites con un parámetro finito (distinto de cero) y el otro que se aproxima a estos límites: [ cita requerida ]
Una aproximación razonable del valor de la mediana de la distribución beta, tanto para α como para β mayores o iguales a uno, viene dada por la fórmula [9]
Cuando α, β ≥ 1, el error relativo (el error absoluto dividido por la mediana) en esta aproximación es menor que 4% y tanto para α ≥ 2 como para β ≥ 2 es menor que 1%. El error absoluto dividido por la diferencia entre la media y la moda es igualmente pequeño:
Significar

El valor esperado (media) ( μ ) de una variable aleatoria de distribución beta X con dos parámetros α y β es una función únicamente de la relación β / α de estos parámetros: [1]
Si en la expresión anterior se toma α = β , se obtiene μ = 1/2 , lo que demuestra que para α = β la media está en el centro de la distribución: es simétrica. Además, se pueden obtener los siguientes límites a partir de la expresión anterior:
Por lo tanto, para β / α → 0, o para α / β → ∞, la media se encuentra en el extremo derecho, x = 1. Para estas razones límite, la distribución beta se convierte en una distribución degenerada de un punto con un pico de función delta de Dirac en el extremo derecho, x = 1 , con probabilidad 1 y probabilidad cero en el resto. Hay una probabilidad del 100 % (certeza absoluta) concentrada en el extremo derecho, x = 1 .
De manera similar, para β / α → ∞, o para α / β → 0, la media se ubica en el extremo izquierdo, x = 0. La distribución beta se convierte en una distribución degenerada de 1 punto con un pico de función delta de Dirac en el extremo izquierdo, x = 0, con probabilidad 1 y probabilidad cero en todos los demás lugares. Hay una probabilidad del 100 % (certeza absoluta) concentrada en el extremo izquierdo, x = 0. A continuación se muestran los límites con un parámetro finito (distinto de cero) y el otro que se acerca a estos límites:
Mientras que para distribuciones unimodales típicas (con modas ubicadas centralmente, puntos de inflexión a ambos lados de la moda y colas más largas) (con Beta( α , β ) tal que α , β > 2 ) se sabe que la media de la muestra (como una estimación de la ubicación) no es tan robusta como la mediana de la muestra, lo opuesto es el caso de distribuciones bimodales uniformes o "en forma de U" (con Beta( α , β ) tal que α , β ≤ 1 ), con las modas ubicadas en los extremos de la distribución. Como señalan Mosteller y Tukey ( [10] p. 207) "el promedio de las dos observaciones extremas utiliza toda la información de la muestra. Esto ilustra cómo, para distribuciones de cola corta, las observaciones extremas deberían tener más peso". Por el contrario, se deduce que la mediana de las distribuciones bimodales "en forma de U" con modas en el borde de la distribución (con Beta( α , β ) tal que α , β ≤ 1 ) no es robusta, ya que la mediana de la muestra excluye las observaciones de muestra extremas de la consideración. Una aplicación práctica de esto ocurre, por ejemplo, para los paseos aleatorios , ya que la probabilidad para el momento de la última visita al origen en un paseo aleatorio se distribuye como la distribución de arcoseno Beta(1/2, 1/2): [5] [11] la media de un número de realizaciones de un paseo aleatorio es un estimador mucho más robusto que la mediana (que es una estimación de medida de muestra inapropiada en este caso).
Media geométrica
_for_Beta_Distribution_versus_alpha_and_beta_from_0_to_2_-_J._Rodal.jpg/440px-(Mean_-_GeometricMean)_for_Beta_Distribution_versus_alpha_and_beta_from_0_to_2_-_J._Rodal.jpg)
,_Yellow=G(1-X),_smaller_values_alpha_and_beta_in_front_-_J._Rodal.jpg/440px-Geometric_Means_for_Beta_distribution_Purple=G(X),_Yellow=G(1-X),_smaller_values_alpha_and_beta_in_front_-_J._Rodal.jpg)
,_Yellow=G(1-X),_larger_values_alpha_and_beta_in_front_-_J._Rodal.jpg/440px-Geometric_Means_for_Beta_distribution_Purple=G(X),_Yellow=G(1-X),_larger_values_alpha_and_beta_in_front_-_J._Rodal.jpg)
El logaritmo de la media geométrica G X de una distribución con variable aleatoria X es la media aritmética de ln( X ), o, equivalentemente, su valor esperado:
Para una distribución beta, la integral del valor esperado da:
donde ψ es la función digamma .
Por lo tanto, la media geométrica de una distribución beta con parámetros de forma α y β es la exponencial de las funciones digamma de α y β como sigue:
Mientras que para una distribución beta con parámetros de forma iguales α = β, se deduce que asimetría = 0 y moda = media = mediana = 1/2, la media geométrica es menor que 1/2: 0 < G X < 1/2 . La razón de esto es que la transformación logarítmica pondera fuertemente los valores de X cercanos a cero, ya que ln( X ) tiende fuertemente hacia el infinito negativo a medida que X se acerca a cero, mientras que ln( X ) se aplana hacia cero a medida que X → 1 .
A lo largo de una línea α = β , se aplican los siguientes límites:
A continuación se presentan los límites con un parámetro finito (distinto de cero) y el otro que se aproxima a estos límites:
El gráfico adjunto muestra la diferencia entre la media y la media geométrica para los parámetros de forma α y β desde cero hasta 2. Además del hecho de que la diferencia entre ellos se acerca a cero a medida que α y β se acercan al infinito y que la diferencia se hace grande para los valores de α y β que se acercan a cero, se puede observar una evidente asimetría de la media geométrica con respecto a los parámetros de forma α y β. La diferencia entre la media geométrica y la media es mayor para valores pequeños de α en relación con β que cuando se intercambian las magnitudes de β y α.
NLJohnson y S. Kotz [1] sugieren la aproximación logarítmica a la función digamma ψ ( α ) ≈ ln( α − 1/2) que da como resultado la siguiente aproximación a la media geométrica:
Los valores numéricos para el error relativo en esta aproximación son los siguientes: [ ( α = β = 1): 9,39 % ]; [ ( α = β =2): 1,29% ]; [ ( α = 2, β = 3): 1,51% ]; [ ( α = 3, β = 2): 0,44% ]; [ ( α = β = 3): 0,51% ]; [ ( α = β = 4): 0,26% ]; [ ( α = 3, β = 4): 0,55% ]; [ ( α = 4, β = 3): 0,24% ].
De manera similar, se puede calcular el valor de los parámetros de forma necesarios para que la media geométrica sea igual a 1/2. Dado el valor del parámetro β , ¿cuál sería el valor del otro parámetro, α , necesario para que la media geométrica sea igual a 1/2?. La respuesta es que (para β > 1 ), el valor de α necesario tiende hacia β + 1/2 cuando β → ∞ . Por ejemplo, todas estas parejas tienen la misma media geométrica de 1/2: [ β = 1, α = 1.4427 ], [ β = 2, α = 2.46958 ], [ β = 3, α = 3.47943 ], [ β = 4, α = 4.48449 ], [ β = 5, α = 5.48756 ], [ β = 10, α = 10,4938 ], [ β = 100, α = 100,499 ].
La propiedad fundamental de la media geométrica, que puede demostrarse falsa para cualquier otra media, es
Esto hace que la media geométrica sea la única media correcta cuando se promedian resultados normalizados , es decir, resultados que se presentan como proporciones de valores de referencia. [12] Esto es relevante porque la distribución beta es un modelo adecuado para el comportamiento aleatorio de los porcentajes y es particularmente adecuada para el modelado estadístico de proporciones. La media geométrica juega un papel central en la estimación de máxima verosimilitud, véase la sección "Estimación de parámetros, máxima verosimilitud". En realidad, cuando se realiza la estimación de máxima verosimilitud, además de la media geométrica G X basada en la variable aleatoria X, también aparece naturalmente otra media geométrica: la media geométrica basada en la transformación lineal –– (1 − X ) , la imagen especular de X , denotada por G (1− X ) :
A lo largo de una línea α = β , se aplican los siguientes límites:
A continuación se presentan los límites con un parámetro finito (distinto de cero) y el otro que se aproxima a estos límites:
Tiene el siguiente valor aproximado:
Aunque tanto G X como G (1− X ) son asimétricas, en el caso de que ambos parámetros de forma sean iguales α = β , las medias geométricas son iguales: G X = G (1− X ) . Esta igualdad se desprende de la siguiente simetría que se muestra entre ambas medias geométricas:
Media armónica

_for_Beta_distribution_versus_alpha_and_beta_from_0_to_2_-_J._Rodal.jpg/440px-(Mean_-_HarmonicMean)_for_Beta_distribution_versus_alpha_and_beta_from_0_to_2_-_J._Rodal.jpg)
,_Yellow=H(1-X),_smaller_values_alpha_and_beta_in_front_-_J._Rodal.jpg/440px-Harmonic_Means_for_Beta_distribution_Purple=H(X),_Yellow=H(1-X),_smaller_values_alpha_and_beta_in_front_-_J._Rodal.jpg)
,_Yellow=H(1-X),_larger_values_alpha_and_beta_in_front_-_J._Rodal.jpg/440px-Harmonic_Means_for_Beta_distribution_Purple=H(X),_Yellow=H(1-X),_larger_values_alpha_and_beta_in_front_-_J._Rodal.jpg)
La inversa de la media armónica ( H X ) de una distribución con variable aleatoria X es la media aritmética de 1/ X o, equivalentemente, su valor esperado. Por lo tanto, la media armónica ( H X ) de una distribución beta con parámetros de forma α y β es:
La media armónica ( H X ) de una distribución beta con α < 1 no está definida, porque su expresión definitoria no está acotada en [0, 1] para un parámetro de forma α menor que la unidad.
Dejando α = β en la expresión anterior se obtiene
mostrando que para α = β la media armónica varía de 0, para α = β = 1, a 1/2, para α = β → ∞.
A continuación se presentan los límites con un parámetro finito (distinto de cero) y el otro que se aproxima a estos límites:
La media armónica desempeña un papel en la estimación de máxima verosimilitud para el caso de cuatro parámetros, además de la media geométrica. En realidad, al realizar la estimación de máxima verosimilitud para el caso de cuatro parámetros, además de la media armónica H X basada en la variable aleatoria X , también aparece naturalmente otra media armónica: la media armónica basada en la transformación lineal (1 − X ), la imagen especular de X , denotada por H 1 − X :
La media armónica ( H (1 − X ) ) de una distribución beta con β < 1 no está definida, porque su expresión definitoria no está acotada en [0, 1] para un parámetro de forma β menor que la unidad.
Dejando α = β en la expresión anterior se obtiene
mostrando que para α = β la media armónica varía de 0, para α = β = 1, a 1/2, para α = β → ∞.
A continuación se presentan los límites con un parámetro finito (distinto de cero) y el otro que se aproxima a estos límites:
Aunque tanto H X como H 1− X son asimétricas, en el caso de que ambos parámetros de forma sean iguales α = β , las medias armónicas son iguales: H X = H 1− X . Esta igualdad se desprende de la siguiente simetría que se muestra entre ambas medias armónicas:
Medidas de dispersión estadística
Diferencia
La varianza (el segundo momento centrado en la media) de una variable aleatoria de distribución beta X con parámetros α y β es: [1] [13]
Dejando α = β en la expresión anterior se obtiene
mostrando que para α = β la varianza disminuye monótonamente a medida que α = β aumenta. Fijando α = β = 0 en esta expresión, se encuentra la varianza máxima var( X ) = 1/4 [1] que solo ocurre al acercarse al límite, en α = β = 0 .
La distribución beta también puede parametrizarse en términos de su media μ (0 < μ < 1) y tamaño de muestra ν = α + β ( ν > 0 ) (ver subsección Media y tamaño de muestra):
Utilizando esta parametrización , se puede expresar la varianza en términos de la media μ y el tamaño de la muestra ν de la siguiente manera:
Dado que ν = α + β > 0 , se deduce que var( X ) < μ (1 − μ ) .
Para una distribución simétrica, la media está en el medio de la distribución, μ = 1/2 , y por lo tanto:
Además, los siguientes límites (con sólo la variable indicada acercándose al límite) se pueden obtener a partir de las expresiones anteriores:
Varianza y covarianza geométrica


El logaritmo de la varianza geométrica, ln(var GX ), de una distribución con variable aleatoria X es el segundo momento del logaritmo de X centrado en la media geométrica de X , ln( G X ):
y por lo tanto, la varianza geométrica es:
En la matriz de información de Fisher , y la curvatura de la función de verosimilitud logarítmica , aparecen el logaritmo de la varianza geométrica de la variable reflejada 1 − X y el logaritmo de la covarianza geométrica entre X y 1 − X :
Para una distribución beta, se pueden derivar momentos logarítmicos de orden superior utilizando la representación de una distribución beta como proporción de dos distribuciones gamma y diferenciando a través de la integral. Se pueden expresar en términos de funciones poligamma de orden superior. Véase la sección § Momentos de variables aleatorias transformadas logarítmicamente. La varianza de las variables logarítmicas y la covarianza de ln X y ln(1− X ) son:
donde la función trigamma , denotada ψ 1 (α), es la segunda de las funciones poligamma , y se define como la derivada de la función digamma :
Por lo tanto,
Los gráficos adjuntos muestran las varianzas geométricas logarítmicas y la covarianza geométrica logarítmica en función de los parámetros de forma α y β . Los gráficos muestran que las varianzas geométricas logarítmicas y la covarianza geométrica logarítmica son cercanas a cero para los parámetros de forma α y β mayores que 2, y que las varianzas geométricas logarítmicas aumentan rápidamente de valor para los valores de los parámetros de forma α y β menores que la unidad. Las varianzas geométricas logarítmicas son positivas para todos los valores de los parámetros de forma. La covarianza geométrica logarítmica es negativa para todos los valores de los parámetros de forma, y alcanza grandes valores negativos para α y β menores que la unidad.
A continuación se presentan los límites con un parámetro finito (distinto de cero) y el otro que se aproxima a estos límites:
Límites con dos parámetros variables:
Aunque tanto ln(var GX ) como ln(var G (1 − X ) ) son asimétricas, cuando los parámetros de forma son iguales, α = β, se tiene: ln(var GX ) = ln(var G(1−X) ). Esta igualdad se desprende de la siguiente simetría que se muestra entre ambas varianzas geométricas logarítmicas:
La covarianza geométrica logarítmica es simétrica:
Desviación absoluta media alrededor de la media


La desviación absoluta media alrededor de la media para la distribución beta con parámetros de forma α y β es: [8]
La desviación absoluta media alrededor de la media es un estimador más robusto de la dispersión estadística que la desviación estándar para distribuciones beta con colas y puntos de inflexión a cada lado de la moda, distribuciones Beta( α , β ) con α , β > 2, ya que depende de las desviaciones lineales (absolutas) en lugar de las desviaciones cuadradas de la media. Por lo tanto, el efecto de desviaciones muy grandes de la media no está tan ponderado.
Utilizando la aproximación de Stirling a la función Gamma , NLJohnson y S.Kotz [1] derivaron la siguiente aproximación para valores de los parámetros de forma mayores que la unidad (el error relativo para esta aproximación es solo −3,5% para α = β = 1, y disminuye a cero cuando α → ∞, β → ∞):
En el límite α → ∞, β → ∞, la razón entre la desviación absoluta media y la desviación estándar (para la distribución beta) se vuelve igual a la razón de las mismas medidas para la distribución normal: . Para α = β = 1 esta razón es igual a , de modo que de α = β = 1 a α, β → ∞ la razón disminuye en un 8,5%. Para α = β = 0 la desviación estándar es exactamente igual a la desviación absoluta media alrededor de la media. Por lo tanto, esta razón disminuye en un 15% de α = β = 0 a α = β = 1, y en un 25% de α = β = 0 a α, β → ∞ . Sin embargo, para distribuciones beta sesgadas tales que α → 0 o β → 0, la relación entre la desviación estándar y la desviación absoluta media se acerca al infinito (aunque cada una de ellas, individualmente, se acerca a cero) porque la desviación absoluta media se acerca a cero más rápido que la desviación estándar.
Utilizando la parametrización en términos de media μ y tamaño de muestra ν = α + β > 0:
- α = μν, β = (1−μ)ν
La desviación absoluta media alrededor de la media se puede expresar en términos de la media μ y el tamaño de la muestra ν de la siguiente manera:
Para una distribución simétrica, la media está en el medio de la distribución, μ = 1/2, y por lo tanto:
Además, los siguientes límites (con sólo la variable indicada acercándose al límite) se pueden obtener a partir de las expresiones anteriores:
Diferencia absoluta media
La diferencia absoluta media para la distribución beta es:
El coeficiente de Gini para la distribución beta es la mitad de la diferencia absoluta media relativa:
Oblicuidad

La asimetría (el tercer momento centrado en la media, normalizado por la potencia 3/2 de la varianza) de la distribución beta es [1]
Si en la expresión anterior se toma α = β, se obtiene γ 1 = 0, lo que demuestra una vez más que para α = β la distribución es simétrica y, por lo tanto, la asimetría es cero. La asimetría es positiva (de cola derecha) para α < β, y negativa (de cola izquierda) para α > β.
Utilizando la parametrización en términos de media μ y tamaño de muestra ν = α + β:
La asimetría se puede expresar en términos de la media μ y el tamaño de la muestra ν de la siguiente manera:
La asimetría también se puede expresar solo en términos de la varianza var y la media μ de la siguiente manera:
El gráfico adjunto de asimetría en función de la varianza y la media muestra que la varianza máxima (1/4) está acoplada con una asimetría cero y la condición de simetría (μ = 1/2), y que la asimetría máxima (infinito positivo o negativo) ocurre cuando la media se ubica en un extremo o en el otro, de modo que la "masa" de la distribución de probabilidad se concentra en los extremos (varianza mínima).
La siguiente expresión para el cuadrado de la asimetría, en términos del tamaño de la muestra ν = α + β y la varianza var , es útil para el método de estimación de momentos de cuatro parámetros:
Esta expresión da correctamente una asimetría de cero para α = β, ya que en ese caso (ver § Varianza): .
Para el caso simétrico (α = β), la asimetría = 0 en todo el rango y se aplican los siguientes límites:
Para los casos asimétricos (α ≠ β) los siguientes límites (con sólo la variable indicada acercándose al límite) se pueden obtener a partir de las expresiones anteriores:
Curtosis

La distribución beta se ha aplicado en el análisis acústico para evaluar el daño a los engranajes, ya que se ha informado que la curtosis de la distribución beta es un buen indicador de la condición de un engranaje. [14] La curtosis también se ha utilizado para distinguir la señal sísmica generada por los pasos de una persona de otras señales. Como las personas u otros objetivos que se mueven en el suelo generan señales continuas en forma de ondas sísmicas, se pueden separar diferentes objetivos en función de las ondas sísmicas que generan. La curtosis es sensible a las señales impulsivas, por lo que es mucho más sensible a la señal generada por los pasos humanos que a otras señales generadas por vehículos, vientos, ruido, etc. [15] Desafortunadamente, la notación para la curtosis no se ha estandarizado. Kenney y Keeping [16] usan el símbolo γ 2 para el exceso de curtosis , pero Abramowitz y Stegun [17] usan una terminología diferente. Para evitar confusiones [18] entre curtosis (el cuarto momento centrado en la media, normalizado por el cuadrado de la varianza) y exceso de curtosis, al utilizar símbolos, se escribirán de la siguiente manera: [8] [19]
Dejando α = β en la expresión anterior se obtiene
- .
Por lo tanto, para distribuciones beta simétricas, el exceso de curtosis es negativo, aumentando desde un valor mínimo de −2 en el límite cuando {α = β} → 0, y acercándose a un valor máximo de cero cuando {α = β} → ∞. El valor de −2 es el valor mínimo de exceso de curtosis que cualquier distribución (no solo las distribuciones beta, sino cualquier distribución de cualquier tipo posible) puede alcanzar. Este valor mínimo se alcanza cuando toda la densidad de probabilidad está completamente concentrada en cada extremo x = 0 y x = 1, sin nada en el medio: una distribución de Bernoulli de 2 puntos con igual probabilidad 1/2 en cada extremo (un lanzamiento de moneda: vea la sección a continuación "Curtosis limitada por el cuadrado de la asimetría" para una discusión más detallada). La descripción de la curtosis como una medida de los "valores atípicos potenciales" (o "valores extremos raros potenciales") de la distribución de probabilidad, es correcta para todas las distribuciones, incluida la distribución beta. Cuando se dan valores extremos poco frecuentes en la distribución beta, mayor es su curtosis; de lo contrario, la curtosis es menor. Para distribuciones beta sesgadas α ≠ β, el exceso de curtosis puede alcanzar valores positivos ilimitados (particularmente para α → 0 para β finito, o para β → 0 para α finito) porque el lado que se aleja de la moda producirá valores extremos ocasionales. La curtosis mínima se produce cuando la densidad de masa se concentra de manera uniforme en cada extremo (y, por lo tanto, la media está en el centro) y no hay densidad de masa de probabilidad entre los extremos.
Utilizando la parametrización en términos de media μ y tamaño de muestra ν = α + β:
Se puede expresar el exceso de curtosis en términos de la media μ y el tamaño de la muestra ν de la siguiente manera:
El exceso de curtosis también se puede expresar en términos de sólo los dos parámetros siguientes: la varianza var y el tamaño de la muestra ν de la siguiente manera:
y, en términos de la varianza var y la media μ como sigue:
El gráfico de exceso de curtosis en función de la varianza y la media muestra que el valor mínimo de exceso de curtosis (−2, que es el valor mínimo posible de exceso de curtosis para cualquier distribución) está íntimamente relacionado con el valor máximo de la varianza (1/4) y la condición de simetría: la media se encuentra en el punto medio (μ = 1/2). Esto ocurre para el caso simétrico de α = β = 0, con asimetría cero. En el límite, esta es la distribución de Bernoulli de 2 puntos con igual probabilidad 1/2 en cada extremo de la función delta de Dirac x = 0 y x = 1 y probabilidad cero en todos los demás lugares. (Un lanzamiento de moneda: una cara de la moneda es x = 0 y la otra cara es x = 1). La varianza es máxima porque la distribución es bimodal sin nada entre los dos modos (picos) en cada extremo. El exceso de curtosis es mínimo: la "masa" de densidad de probabilidad es cero en la media y se concentra en los dos picos de cada extremo. El exceso de curtosis alcanza el valor mínimo posible (para cualquier distribución) cuando la función de densidad de probabilidad tiene dos picos en cada extremo: es bi-"pico" sin nada entre ellos.
Por otra parte, el gráfico muestra que para los casos extremadamente sesgados, donde la media se ubica cerca de uno u otro extremo (μ = 0 o μ = 1), la varianza es cercana a cero y el exceso de curtosis se acerca rápidamente al infinito cuando la media de la distribución se acerca a cualquiera de los extremos.
Alternativamente, el exceso de curtosis también se puede expresar en términos de sólo los dos parámetros siguientes: el cuadrado de la asimetría y el tamaño de la muestra ν de la siguiente manera:
A partir de esta última expresión, se pueden obtener los mismos límites publicados hace más de un siglo por Karl Pearson [20] para la distribución beta (véase la sección siguiente titulada "Curtosis limitada por el cuadrado de la asimetría"). Si se establece α + β = ν = 0 en la expresión anterior, se obtiene el límite inferior de Pearson (los valores de asimetría y exceso de curtosis por debajo del límite (exceso de curtosis + 2 − asimetría 2 = 0) no pueden darse para ninguna distribución, y por lo tanto Karl Pearson llamó apropiadamente a la región por debajo de este límite la "región imposible"). El límite de α + β = ν → ∞ determina el límite superior de Pearson.
por lo tanto:
Los valores de ν = α + β tales que ν varía de cero a infinito, 0 < ν < ∞, abarcan toda la región de la distribución beta en el plano de exceso de curtosis versus asimetría al cuadrado.
Para el caso simétrico ( α = β ), se aplican los siguientes límites:
Para los casos asimétricos ( α ≠ β ) los siguientes límites (con sólo la variable indicada acercándose al límite) se pueden obtener a partir de las expresiones anteriores:
Función característica
_Beta_Distr_alpha=beta_from_0_to_25_Back_-_J._Rodal.jpg/440px-Re(CharacteristicFunction)_Beta_Distr_alpha=beta_from_0_to_25_Back_-_J._Rodal.jpg)
_Beta_Distr_alpha=beta_from_0_to_25_Front-_J._Rodal.jpg/440px-Re(CharacteristicFunc)_Beta_Distr_alpha=beta_from_0_to_25_Front-_J._Rodal.jpg)
_Beta_Distr_alpha_from_0_to_25_and_beta=alpha+0.5_Back_-_J._Rodal.jpg/440px-Re(CharacteristFunc)_Beta_Distr_alpha_from_0_to_25_and_beta=alpha+0.5_Back_-_J._Rodal.jpg)
_Beta_Distrib._beta_from_0_to_25,_alpha=beta+0.5_Back_-_J._Rodal.jpg/440px-Re(CharacterFunc)_Beta_Distrib._beta_from_0_to_25,_alpha=beta+0.5_Back_-_J._Rodal.jpg)
_Beta_Distr._beta_from_0_to_25,_alpha=beta+0.5_Front_-_J._Rodal.jpg/440px-Re(CharacterFunc)_Beta_Distr._beta_from_0_to_25,_alpha=beta+0.5_Front_-_J._Rodal.jpg)
La función característica es la transformada de Fourier de la función de densidad de probabilidad. La función característica de la distribución beta es la función hipergeométrica confluente de Kummer (de primera especie): [1] [17] [21]
dónde
es el factorial ascendente , también llamado "símbolo de Pochhammer". El valor de la función característica para t = 0, es uno:
Además, las partes reales e imaginarias de la función característica disfrutan de las siguientes simetrías con respecto al origen de la variable t :
El caso simétrico α = β simplifica la función característica de la distribución beta a una función de Bessel , ya que en el caso especial α + β = 2α la función hipergeométrica confluente (de primer tipo) se reduce a una función de Bessel (la función de Bessel modificada de primer tipo ) utilizando la segunda transformación de Kummer de la siguiente manera:
En los gráficos adjuntos, se muestra la parte real (Re) de la función característica de la distribución beta para casos simétricos (α = β) y sesgados (α ≠ β).
Otros momentos
Función generadora de momentos
También se deduce [1] [8] que la función generadora de momentos es
En particular MX ( α ; β ; 0) = 1.
Momentos más elevados
Utilizando la función generadora de momentos , el k -ésimo momento bruto se da por [1] el factor
multiplicando el término (serie exponencial) en la serie de la función generadora de momentos
donde ( x ) ( k ) es un símbolo de Pochhammer que representa un factorial ascendente. También se puede escribir en forma recursiva como
Dado que la función generadora de momentos tiene un radio de convergencia positivo, la distribución beta está determinada por sus momentos . [22]
Momentos de variables aleatorias transformadas
Momentos de variables aleatorias transformadas linealmente, producto e invertidas
También se pueden mostrar las siguientes expectativas para una variable aleatoria transformada, [1] donde la variable aleatoria X tiene una distribución Beta con parámetros α y β : X ~ Beta( α , β ). El valor esperado de la variable 1 − X es la simetría especular del valor esperado basado en X :
Debido a la simetría especular de la función de densidad de probabilidad de la distribución beta, las varianzas basadas en las variables X y 1 − X son idénticas, y la covarianza en X (1 − X es el negativo de la varianza:
Estos son los valores esperados para las variables invertidas (están relacionadas con las medias armónicas, ver § Media armónica):
La siguiente transformación, que consiste en dividir la variable X por su imagen especular X /(1 − X ), da como resultado el valor esperado de la "distribución beta invertida" o distribución beta prima (también conocida como distribución beta de segundo tipo o distribución beta tipo VI de Pearson ): [1]
Las varianzas de estas variables transformadas se pueden obtener mediante integración, como los valores esperados de los segundos momentos centrados en las variables correspondientes:
La siguiente varianza de la variable X dividida por su imagen especular ( X /(1− X ) da como resultado la varianza de la "distribución beta invertida" o distribución beta prima (también conocida como distribución beta de segundo tipo o tipo VI de Pearson ): [1]
Las covarianzas son:
Estas expectativas y variaciones aparecen en la matriz de información de Fisher de cuatro parámetros (§ Información de Fisher).
Momentos de variables aleatorias transformadas logarítmicamente
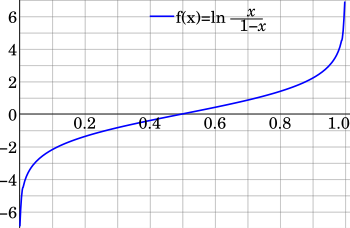
En esta sección se analizan los valores esperados para las transformaciones logarítmicas (útiles para las estimaciones de máxima verosimilitud , véase § Estimación de parámetros, Máxima verosimilitud). Las siguientes transformaciones lineales logarítmicas están relacionadas con las medias geométricas G X y G (1− X ) (véase § Media geométrica):
Donde la función digamma ψ(α) se define como la derivada logarítmica de la función gamma : [17]
Las transformaciones logit son interesantes, [23] ya que generalmente transforman varias formas (incluidas las formas J) en densidades en forma de campana (generalmente sesgadas) sobre la variable logit, y pueden eliminar las singularidades finales sobre la variable original:
Johnson [24] consideró la distribución de la variable transformada logit ln( X /1 − X ), incluyendo su función generadora de momentos y aproximaciones para valores grandes de los parámetros de forma. Esta transformación extiende el soporte finito [0, 1] basado en la variable original X a un soporte infinito en ambas direcciones de la línea real (−∞, +∞). El logit de una variable beta tiene la distribución logística-beta .
Los momentos logarítmicos de orden superior se pueden derivar utilizando la representación de una distribución beta como proporción de dos distribuciones gamma y diferenciándolas mediante la integral. Se pueden expresar en términos de funciones poligamma de orden superior de la siguiente manera:
Por lo tanto, la varianza de las variables logarítmicas y la covarianza de ln( X ) y ln(1− X ) son:
donde la función trigamma , denotada ψ 1 ( α ), es la segunda de las funciones poligamma , y se define como la derivada de la función digamma :
Las varianzas y covarianzas de las variables transformadas logarítmicamente X y (1 − X ) son diferentes, en general, porque la transformación logarítmica destruye la simetría especular de las variables originales X y (1 − X ), a medida que el logaritmo se acerca al infinito negativo para la variable que se acerca a cero.
Estas varianzas y covarianzas logarítmicas son los elementos de la matriz de información de Fisher para la distribución beta. También son una medida de la curvatura de la función de verosimilitud logarítmica (véase la sección sobre Estimación de máxima verosimilitud).
Las varianzas de las variables inversas logarítmicas son idénticas a las varianzas de las variables logarítmicas:
También se deduce que las varianzas de las variables transformadas logit son
Cantidades de información (entropía)
Dada una variable aleatoria distribuida beta, X ~ Beta( α , β ), la entropía diferencial de X es (medida en nats ), [25] el valor esperado del negativo del logaritmo de la función de densidad de probabilidad :
donde f ( x ; α , β ) es la función de densidad de probabilidad de la distribución beta:
La función digamma ψ aparece en la fórmula de la entropía diferencial como consecuencia de la fórmula integral de Euler para los números armónicos que se desprende de la integral:
La entropía diferencial de la distribución beta es negativa para todos los valores de α y β mayores que cero, excepto en α = β = 1 (para cuyos valores la distribución beta es la misma que la distribución uniforme ), donde la entropía diferencial alcanza su valor máximo de cero. Es de esperar que la entropía máxima se produzca cuando la distribución beta se vuelve igual a la distribución uniforme, ya que la incertidumbre es máxima cuando todos los eventos posibles son equiprobables.
Para α o β que se acercan a cero, la entropía diferencial se acerca a su valor mínimo de infinito negativo. Para (cualquiera o ambos) α o β que se acercan a cero, hay una cantidad máxima de orden: toda la densidad de probabilidad se concentra en los extremos, y hay densidad de probabilidad cero en los puntos ubicados entre los extremos. De manera similar, para (cualquiera o ambos) α o β que se acercan al infinito, la entropía diferencial se acerca a su valor mínimo de infinito negativo y una cantidad máxima de orden. Si α o β se acercan al infinito (y el otro es finito) toda la densidad de probabilidad se concentra en un extremo, y la densidad de probabilidad es cero en todos los demás lugares. Si ambos parámetros de forma son iguales (el caso simétrico), α = β , y se acercan al infinito simultáneamente, la densidad de probabilidad se convierte en un pico ( función delta de Dirac ) concentrado en el medio x = 1/2, y por lo tanto hay 100% de probabilidad en el medio x = 1/2 y probabilidad cero en todos los demás lugares.
La entropía diferencial (del caso continuo) fue introducida por Shannon en su artículo original (donde la llamó la "entropía de una distribución continua"), como la parte final del mismo artículo donde definió la entropía discreta . [26] Desde entonces se sabe que la entropía diferencial puede diferir del límite infinitesimal de la entropía discreta por un desplazamiento infinito, por lo tanto, la entropía diferencial puede ser negativa (como lo es para la distribución beta). Lo que realmente importa es el valor relativo de la entropía.
Dadas dos variables aleatorias distribuidas beta, X 1 ~ Beta( α , β ) y X 2 ~ Beta( α ′ , β ′ ), la entropía cruzada es (medida en nats) [27]
La entropía cruzada se ha utilizado como métrica de error para medir la distancia entre dos hipótesis. [28] [29] Su valor absoluto es mínimo cuando las dos distribuciones son idénticas. Es la medida de información más estrechamente relacionada con el logaritmo de máxima verosimilitud [27] (ver apartado sobre "Estimación de parámetros. Estimación de máxima verosimilitud").
La entropía relativa, o divergencia de Kullback–Leibler D KL ( X 1 || X 2 ), es una medida de la ineficiencia de suponer que la distribución es X 2 ~ Beta( α ′ , β ′ ) cuando la distribución es realmente X 1 ~ Beta( α , β ). Se define de la siguiente manera (medida en nats).
La entropía relativa, o divergencia de Kullback–Leibler , siempre es no negativa. A continuación se presentan algunos ejemplos numéricos:
- X 1 ~ Beta(1, 1) y X 2 ~ Beta(3, 3); D KL ( X 1 || X 2 ) = 0,598803; D KL ( X 2 || X 1 ) = 0,267864; h ( X 1 ) = 0; h ( X 2 ) = −0,267864
- X 1 ~ Beta(3, 0,5) y X 2 ~ Beta(0,5, 3); D KL ( X 1 || X 2 ) = 7,21574; D KL ( X 2 || X 1 ) = 7,21574; h ( X 1 ) = −1,10805; h ( X 2 ) = −1,10805.
La divergencia de Kullback–Leibler no es simétrica D KL ( X 1 || X 2 ) ≠ D KL ( X 2 || X 1 ) para el caso en el que las distribuciones beta individuales Beta(1, 1) y Beta(3, 3) son simétricas, pero tienen diferentes entropías h ( X 1 ) ≠ h ( X 2 ). El valor de la divergencia de Kullback depende de la dirección recorrida: si se va de una entropía (diferencial) más alta a una entropía (diferencial) más baja o al revés. En el ejemplo numérico anterior, la divergencia de Kullback mide la ineficiencia de suponer que la distribución es (en forma de campana) Beta(3, 3), en lugar de (uniforme) Beta(1, 1). La entropía "h" de Beta(1, 1) es mayor que la entropía "h" de Beta(3, 3) porque la distribución uniforme Beta(1, 1) tiene una cantidad máxima de desorden. La divergencia de Kullback es más de dos veces mayor (0,598803 en lugar de 0,267864) cuando se mide en la dirección de la entropía decreciente: la dirección que supone que la distribución (uniforme) Beta(1, 1) es (en forma de campana) Beta(3, 3) en lugar de lo contrario. En este sentido restringido, la divergencia de Kullback es consistente con la segunda ley de la termodinámica .
La divergencia de Kullback-Leibler es simétrica D KL ( X 1 || X 2 ) = D KL ( X 2 || X 1 ) para los casos sesgados Beta(3, 0.5) y Beta(0.5, 3) que tienen igual entropía diferencial h ( X 1 ) = h ( X 2 ).
La condición de simetría:
se desprende de las definiciones anteriores y de la simetría especular f ( x ; α , β ) = f (1 − x ; α , β ) de la que disfruta la distribución beta.
Relaciones entre medidas estadísticas
Relación entre media, moda y mediana
Si 1 < α < β entonces moda ≤ mediana ≤ media. [9] Expresando la moda (sólo para α, β > 1), y la media en términos de α y β:
Si 1 < β < α entonces el orden de las desigualdades se invierte. Para α, β > 1 la distancia absoluta entre la media y la mediana es menor que el 5% de la distancia entre los valores máximo y mínimo de x . Por otra parte, la distancia absoluta entre la media y la moda puede alcanzar el 50% de la distancia entre los valores máximo y mínimo de x , para el caso ( patológico ) de α = 1 y β = 1, para cuyos valores la distribución beta se aproxima a la distribución uniforme y la entropía diferencial se aproxima a su valor máximo , y por tanto al máximo "desorden".
Por ejemplo, para α = 1,0001 y β = 1,00000001:
- modo = 0,9999; PDF(modo) = 1,00010
- media = 0,500025; PDF(media) = 1,00003
- mediana = 0,500035; PDF(mediana) = 1,00003
- media − moda = −0,499875
- media − mediana = −9,65538 × 10 −6
donde PDF representa el valor de la función de densidad de probabilidad .
Relación entre media, media geométrica y media armónica

De la desigualdad de las medias aritmética y geométrica se sabe que la media geométrica es menor que la media. De manera similar, la media armónica es menor que la media geométrica. El gráfico adjunto muestra que para α = β, tanto la media como la mediana son exactamente iguales a 1/2, independientemente del valor de α = β, y la moda también es igual a 1/2 para α = β > 1, sin embargo, las medias geométrica y armónica son menores que 1/2 y solo se aproximan a este valor asintóticamente cuando α = β → ∞.
Curtosis limitada por el cuadrado de la asimetría

Como señaló Feller , [5] en el sistema de Pearson la densidad de probabilidad beta aparece como tipo I (cualquier diferencia entre la distribución beta y la distribución tipo I de Pearson es solo superficial y no hace ninguna diferencia para la siguiente discusión sobre la relación entre curtosis y asimetría). Karl Pearson mostró, en la Placa 1 de su artículo [20] publicado en 1916, un gráfico con la curtosis como eje vertical ( ordenada ) y el cuadrado de la asimetría como eje horizontal ( abscisa ), en el que se mostraban varias distribuciones. [30] La región ocupada por la distribución beta está limitada por las siguientes dos líneas en el plano (asimetría 2 ,curtosis) o el plano (asimetría 2 ,exceso de curtosis) :
o, equivalentemente,
En una época en la que no existían ordenadores digitales potentes, Karl Pearson calculó con precisión otros límites, [31] [20] por ejemplo, separando las distribuciones "en forma de U" de las "en forma de J". La línea límite inferior (exceso de curtosis + 2 − asimetría 2 = 0) se produce por distribuciones beta sesgadas "en forma de U" con valores de los parámetros de forma α y β cercanos a cero. La línea límite superior (exceso de curtosis − (3/2) asimetría 2 = 0) se produce por distribuciones extremadamente sesgadas con valores muy grandes de uno de los parámetros y valores muy pequeños del otro parámetro. Karl Pearson demostró [20] que esta línea límite superior (exceso de curtosis − (3/2) asimetría 2 = 0) es también la intersección con la distribución III de Pearson, que tiene soporte ilimitado en una dirección (hacia el infinito positivo), y puede tener forma de campana o de J. Su hijo, Egon Pearson , demostró [30] que la región (en el plano de curtosis/asimetría al cuadrado) ocupada por la distribución beta (equivalentemente, la distribución I de Pearson) a medida que se aproxima a este límite (exceso de curtosis − (3/2) asimetría 2 = 0) se comparte con la distribución chi-cuadrado no central . Karl Pearson [32] (Pearson 1895, pp. 357, 360, 373–376) también demostró que la distribución gamma es una distribución tipo III de Pearson. Por lo tanto, esta línea límite para la distribución tipo III de Pearson se conoce como la línea gamma. (Esto se puede demostrar a partir del hecho de que el exceso de curtosis de la distribución gamma es 6/ k y el cuadrado de la asimetría es 4/ k , por lo tanto (exceso de curtosis − (3/2) asimetría 2 = 0) se satisface de forma idéntica por la distribución gamma independientemente del valor del parámetro "k"). Pearson señaló posteriormente que la distribución chi-cuadrado es un caso especial del tipo III de Pearson y también comparte esta línea límite (como es evidente a partir del hecho de que para la distribución chi-cuadrado el exceso de curtosis es 12/ k y el cuadrado de la asimetría es 8/ k , por lo tanto (exceso de curtosis − (3/2) asimetría 2 = 0) se satisface de forma idéntica independientemente del valor del parámetro "k"). Esto es de esperarse, ya que la distribución chi-cuadrado X ~ χ 2 ( k ) es un caso especial de la distribución gamma, con parametrización X ~ Γ(k/2, 1/2) donde k es un entero positivo que especifica el "número de grados de libertad" de la distribución chi-cuadrado.
Un ejemplo de una distribución beta cerca del límite superior (exceso de curtosis − (3/2) asimetría 2 = 0) viene dado por α = 0,1, β = 1000, para el que la relación (exceso de curtosis)/(asimetría 2 ) = 1,49835 se acerca al límite superior de 1,5 desde abajo. Un ejemplo de una distribución beta cerca del límite inferior (exceso de curtosis + 2 − asimetría 2 = 0) viene dado por α = 0,0001, β = 0,1, para cuyos valores la expresión (exceso de curtosis + 2)/(asimetría 2 ) = 1,01621 se acerca al límite inferior de 1 desde arriba. En el límite infinitesimal para α y β que se acerca a cero simétricamente, el exceso de curtosis alcanza su valor mínimo en −2. Este valor mínimo se produce en el punto en el que la línea límite inferior interseca el eje vertical ( ordenada ). (Sin embargo, en el gráfico original de Pearson, la ordenada es la curtosis, en lugar del exceso de curtosis, y aumenta hacia abajo en lugar de hacia arriba).
Los valores de asimetría y exceso de curtosis por debajo del límite inferior (exceso de curtosis + 2 − asimetría 2 = 0) no pueden ocurrir para ninguna distribución, y por lo tanto Karl Pearson apropiadamente llamó a la región por debajo de este límite la "región imposible". El límite para esta "región imposible" está determinado por distribuciones bimodales en forma de U (simétricas o sesgadas) para las cuales los parámetros α y β tienden a cero y por lo tanto toda la densidad de probabilidad se concentra en los extremos: x = 0, 1 con prácticamente nada entre ellos. Dado que para α ≈ β ≈ 0 la densidad de probabilidad se concentra en los dos extremos x = 0 y x = 1, este "límite imposible" está determinado por una distribución de Bernoulli , donde los dos únicos resultados posibles ocurren con probabilidades respectivas p y q = 1− p . Para los casos que se aproximan a este límite con simetría α = β, asimetría ≈ 0, exceso de curtosis ≈ −2 (este es el exceso de curtosis más bajo posible para cualquier distribución), y las probabilidades son p ≈ q ≈ 1/2. Para los casos que se aproximan a este límite con asimetría, exceso de curtosis ≈ −2 + asimetría 2 , y la densidad de probabilidad se concentra más en un extremo que en el otro (prácticamente sin nada en el medio), con probabilidades en el extremo izquierdo x = 0 y en el extremo derecho x = 1.
Simetría
Todas las afirmaciones están condicionadas a que α , β > 0:
- Función de densidad de probabilidad reflexión simetría
- Función de distribución acumulativa simetría de reflexión más traslación unitaria
- Simetría de reflexión modal más traslación unitaria
- Simetría de reflexión media más traslación unitaria
- Simetría de reflexión media más traslación unitaria
- Las medias geométricas son individualmente asimétricas, la siguiente simetría se aplica entre la media geométrica basada en X y la media geométrica basada en su reflexión (1-X)
- Armónico significa que cada uno es individualmente asimétrico, la siguiente simetría se aplica entre la media armónica basada en X y la media armónica basada en su reflexión (1-X)
- .
- Simetría de varianza
- Cada variación geométrica es individualmente asimétrica, la siguiente simetría se aplica entre la varianza geométrica logarítmica basada en X y la varianza geométrica logarítmica basada en su reflexión (1-X)
- Simetría de covarianza geométrica
- Desviación absoluta media alrededor de la simetría media
- Asimetría asimétrica
- Simetría de curtosis excesiva
- Simetría de la función característica de la parte real (con respecto al origen de la variable "t")
- Función característica de simetría oblicua de la parte imaginaria (con respecto al origen de la variable "t")
- Simetría de la función característica del valor absoluto (con respecto al origen de la variable "t")
- Simetría de entropía diferencial
- Simetría de entropía relativa (también llamada divergencia de Kullback-Leibler )
- Simetría de la matriz de información de Fisher
Geometría de la función de densidad de probabilidad
Puntos de inflexión


Para ciertos valores de los parámetros de forma α y β, la función de densidad de probabilidad tiene puntos de inflexión en los que la curvatura cambia de signo. La posición de estos puntos de inflexión puede ser útil como medida de la dispersión o extensión de la distribución.
Definiendo la siguiente cantidad:
Los puntos de inflexión ocurren, [1] [7] [8] [19] dependiendo del valor de los parámetros de forma α y β, de la siguiente manera:
- (α > 2, β > 2) La distribución tiene forma de campana (simétrica para α = β y sesgada en caso contrario), con dos puntos de inflexión , equidistantes de la moda:
- (α = 2, β > 2) La distribución es unimodal, sesgada positivamente, de cola derecha, con un punto de inflexión , ubicado a la derecha de la moda:
- (α > 2, β = 2) La distribución es unimodal, sesgada negativamente, de cola izquierda, con un punto de inflexión , ubicado a la izquierda de la moda:
- (1 < α < 2, β > 2, α+β>2) La distribución es unimodal, sesgada positivamente, de cola derecha, con un punto de inflexión , ubicado a la derecha de la moda:
- (0 < α < 1, 1 < β < 2) La distribución tiene una moda en el extremo izquierdo x = 0 y está sesgada positivamente, con cola derecha. Hay un punto de inflexión , ubicado a la derecha de la moda:
- (α > 2, 1 < β < 2) La distribución es unimodal sesgada negativamente, de cola izquierda, con un punto de inflexión , ubicado a la izquierda de la moda:
- (1 < α < 2, 0 < β < 1) La distribución tiene una moda en el extremo derecho x = 1 y está sesgada negativamente, con cola izquierda. Hay un punto de inflexión , ubicado a la izquierda de la moda:
No hay puntos de inflexión en las regiones restantes (simétricas y sesgadas): en forma de U: (α, β < 1), en forma de U invertida: (1 < α < 2, 1 < β < 2), en forma de J invertida (α < 1, β > 2) o en forma de J: (α > 2, β < 1)
Los gráficos adjuntos muestran las ubicaciones de los puntos de inflexión (mostrados verticalmente, que van de 0 a 1) en comparación con α y β (los ejes horizontales que van de 0 a 5). Hay grandes cortes en las superficies que intersecan las líneas α = 1, β = 1, α = 2 y β = 2 porque en estos valores la distribución beta cambia de 2 modos a 1 modo y a ningún modo.
Formas





La función de densidad beta puede adoptar una amplia variedad de formas diferentes según los valores de los dos parámetros α y β . La capacidad de la distribución beta de adoptar esta gran diversidad de formas (utilizando solo dos parámetros) es en parte responsable de que se le haya encontrado una amplia aplicación para modelar mediciones reales:
Simétrico (alfa=β)
- La función de densidad es simétrica alrededor de 1/2 (gráficos azul y verde azulado).
- mediana = media = 1/2.
- asimetría = 0.
- varianza = 1/(4(2α + 1))
- α = β < 1
- En forma de U (gráfico azul).
- bimodal: modo izquierdo = 0, modo derecho = 1, antimodo = 1/2
- 1/12 < var( X ) < 1/4 [1]
- −2 < exceso de curtosis( X ) < −6/5
- α = β = 1/2 es la distribución del arcoseno
- var( X ) = 1/8
- exceso de curtosis( X ) = −3/2
- CF = Rinc (t) [33]
- α = β → 0 es una distribución de Bernoulli de 2 puntos con probabilidad igual 1/2 en cada extremo de la función delta de Dirac x = 0 y x = 1 y probabilidad cero en todos los demás extremos. Lanzamiento de una moneda: una cara de la moneda es x = 0 y la otra cara es x = 1.
- Un valor inferior a éste es imposible de alcanzar para cualquier distribución.
- La entropía diferencial se acerca a un valor mínimo de −∞
- α = β = 1
- la distribución uniforme [0, 1]
- Sin modo
- var( X ) = 1/12
- exceso de curtosis( X ) = −6/5
- La entropía diferencial (negativa en cualquier otro lugar) alcanza su valor máximo de cero.
- CF = Sinc (t)
- α = β > 1
- unimodal simétrico
- moda = 1/2.
- 0 < var( X ) < 1/12 [1]
- −6/5 < exceso de curtosis( X ) < 0
- α = β = 3/2 es una distribución semielíptica [0, 1], véase: Distribución de semicírculo de Wigner [34]
- var( X ) = 1/16.
- exceso de curtosis( X ) = −1
- CF = 2 Jinc (t)
- α = β = 2 es la distribución parabólica [0, 1]
- var( X ) = 1/20
- exceso de curtosis( X ) = −6/7
- CF = 3 Tinc (t) [35]
- α = β > 2 tiene forma de campana, con puntos de inflexión ubicados a cada lado del modo.
- 0 < var( X ) < 1/20
- −6/7 < exceso de curtosis( X ) < 0
- α = β → ∞ es una distribución degenerada de 1 punto con un pico de la función delta de Dirac en el punto medio x = 1/2 con probabilidad 1 y probabilidad cero en el resto de los puntos. Hay una probabilidad del 100 % (certeza absoluta) concentrada en el único punto x = 1/2.
- La entropía diferencial se acerca a un valor mínimo de −∞
Sesgado (alfa≠β)
La función de densidad está sesgada . Un intercambio de valores de parámetros produce la imagen especular (el reverso) de la curva inicial. Algunos casos más específicos:
- α < 1, β < 1
- En forma de U
- Sesgo positivo para α < β, sesgo negativo para α > β.
- bimodal: modo izquierdo = 0, modo derecho = 1, antimodo =
- 0 < mediana < 1.
- 0 < var( X ) < 1/4
- α > 1, β > 1
- Unimodal (gráficos magenta y cian),
- Sesgo positivo para α < β, sesgo negativo para α > β.
- 0 < mediana < 1
- 0 < var( X ) < 1/12
- α < 1, β ≥ 1
- en forma de J invertida con cola derecha,
- sesgado positivamente,
- estrictamente decreciente, convexo
- modo = 0
- 0 < mediana < 1/2.
- (la varianza máxima ocurre para , o α = Φ el conjugado de la proporción áurea )
- α ≥ 1, β < 1
- En forma de J con cola izquierda,
- sesgado negativamente,
- estrictamente creciente, convexo
- modo = 1
- 1/2 < mediana < 1
- (la varianza máxima ocurre para , o β = Φ el conjugado de la proporción áurea )
- α = 1, β > 1
- sesgado positivamente,
- estrictamente decreciente (gráfico rojo),
- una distribución de función de potencia invertida (imagen especular) [0,1]
- media = 1 / (β + 1)
- mediana = 1 - 1/2 1/β
- modo = 0
- α = 1, 1 < β < 2
- cóncavo
- 1/18 < var( X ) < 1/12.
- α = 1, β = 2
- una línea recta con pendiente −2, la distribución triangular recta con ángulo recto en el extremo izquierdo, en x = 0
- var( X ) = 1/18
- α = 1, β > 2
- en forma de J invertida con cola derecha,
- convexo
- 0 < var( X ) < 1/18
- α > 1, β = 1
- sesgado negativamente,
- estrictamente creciente (gráfico verde),
- La distribución de la función de potencia [0, 1] [8]
- media = α / (α + 1)
- mediana = 1/2 1/α
- modo = 1
- 2 > α > 1, β = 1
- cóncavo
- 1/18 < var( X ) < 1/12
- α = 2, β = 1
- una línea recta con pendiente +2, la distribución triangular recta con ángulo recto en el extremo derecho, en x = 1
- var( X ) = 1/18
- α > 2, β = 1
- En forma de J con cola izquierda, convexa.
- 0 < var( X ) < 1/18
Distribuciones relacionadas
Transformaciones
- Si X ~ Beta( α , β ) entonces 1 − X ~ Beta( β , α ) simetría de imagen especular
- Si X ~ Beta( α , β ) entonces . La distribución beta prima , también llamada "distribución beta de segundo tipo".
- Si , entonces tiene una distribución logística generalizada , con densidad , donde es la sigmoide logística .
- Si X ~ Beta( α , β ) entonces .
- Si X ~ Beta( n /2, m /2) entonces (asumiendo que n > 0 y m > 0), la distribución F de Fisher–Snedecor .
- Si entonces min + X (max − min) ~ PERT(min, max, m , λ ) donde PERT denota una distribución PERT utilizada en el análisis PERT , y m = valor más probable. [36] Tradicionalmente [37] λ = 4 en el análisis PERT.
- Si X ~ Beta(1, β ) entonces X ~ Distribución de Kumaraswamy con parámetros (1, β )
- Si X ~ Beta( α , 1) entonces X ~ Distribución de Kumaraswamy con parámetros ( α , 1)
- Si X ~ Beta( α , 1) entonces −ln( X ) ~ Exponencial( α )
Casos especiales y limitantes

- Beta(1, 1) ~ U(0, 1) con densidad 1 en ese intervalo.
- Beta(n, 1) ~ Máximo de n variables aleatorias independientes con U(0, 1) , a veces llamada distribución de función de potencia estándar con densidad n x n –1 en ese intervalo.
- Beta(1, n) ~ Mínimo de n variables aleatorias independientes con U(0, 1) con densidad n (1 − x ) n −1 en ese intervalo.
- Si X ~ Beta(3/2, 3/2) y r > 0 entonces 2 rX − r ~ distribución de semicírculo de Wigner .
- Beta(1/2, 1/2) es equivalente a la distribución de arcoseno . Esta distribución es también la probabilidad previa de Jeffreys para las distribuciones de Bernoulli y binomial . La densidad de probabilidad de arcoseno es una distribución que aparece en varios teoremas fundamentales de caminata aleatoria. En una caminata aleatoria de lanzamiento de moneda justo , la probabilidad para el momento de la última visita al origen se distribuye como una distribución de arcoseno (en forma de U) . [5] [11] En un juego de lanzamiento de moneda justo de dos jugadores, se dice que un jugador está a la cabeza si la caminata aleatoria (que comenzó en el origen) está por encima del origen. El número más probable de veces que un jugador dado estará a la cabeza, en un juego de longitud 2 N , no es N. Por el contrario, N es el número menos probable de veces que el jugador estará a la cabeza. El número más probable de veces a la cabeza es 0 o 2 N (siguiendo la distribución de arcoseno ).
- La distribución exponencial .
- La distribución gamma .
- Para valores grandes , la distribución normal . Más precisamente, si entonces converge en distribución a una distribución normal con media 0 y varianza a medida que n aumenta.
Derivado de otras distribuciones
- La estadística de orden k de una muestra de tamaño n de la distribución uniforme es una variable aleatoria beta, U ( k ) ~ Beta( k , n +1− k ). [38]
- Si X ~ Gamma(α, θ) e Y ~ Gamma(β, θ) son independientes, entonces .
- Si y son independientes, entonces .
- Si X ~ U(0, 1) y α > 0 entonces X 1/ α ~ Beta( α , 1). Distribución de la función potencia.
- Si [ aclaración necesaria ] , entonces [ aclaración necesaria ] para valores discretos de n y k donde y . [39]
- Si X ~ Cauchy(0, 1) entonces
Combinación con otras distribuciones
- X ~ Beta( α , β ) y Y ~ F(2 β ,2 α ) entonces para todo x > 0.
Composición con otras distribuciones
- Si p ~ Beta(α, β) y X ~ Bin( k , p ) entonces X ~ distribución beta-binomial
- Si p ~ Beta(α, β) y X ~ NB( r , p ) entonces X ~ distribución binomial negativa beta
Generalizaciones
- La generalización a múltiples variables, es decir, una distribución Beta multivariante , se denomina distribución de Dirichlet . Las marginales univariadas de la distribución de Dirichlet tienen una distribución Beta. La distribución Beta es conjugada con las distribuciones binomial y de Bernoulli exactamente de la misma manera que la distribución de Dirichlet es conjugada con la distribución multinomial y la distribución categórica .
- La distribución tipo I de Pearson es idéntica a la distribución beta (excepto por el desplazamiento arbitrario y el reescalamiento que también se pueden lograr con la parametrización de cuatro parámetros de la distribución beta).
- La distribución beta es el caso especial de la distribución beta no central donde : .
- La distribución beta generalizada es una familia de distribuciones de cinco parámetros que tiene la distribución beta como un caso especial.
- La distribución beta de matriz variable es una distribución para matrices definidas positivas .
Inferencia estadística
Estimación de parámetros
Método de momentos
Dos parámetros desconocidos
Se pueden estimar dos parámetros desconocidos ( de una distribución beta admitida en el intervalo [0,1]), utilizando el método de momentos, con los dos primeros momentos (media de la muestra y varianza de la muestra) de la siguiente manera. Sea:
sea la estimación de la media muestral y
sea la estimación de la varianza de la muestra . Las estimaciones de los parámetros mediante el método de momentos son
- si
- si
Cuando se requiere la distribución sobre un intervalo conocido distinto de [0, 1] con la variable aleatoria X , digamos [ a , c ] con la variable aleatoria Y , entonces reemplace con y con en el par de ecuaciones anteriores para los parámetros de forma (vea la sección "Cuatro parámetros desconocidos" a continuación), [40] donde:
Cuatro parámetros desconocidos

Los cuatro parámetros ( de una distribución beta soportada en el intervalo [ a , c ], ver sección "Parametrizaciones alternativas, Cuatro parámetros") pueden estimarse, utilizando el método de momentos desarrollado por Karl Pearson , igualando los valores de la muestra y la población de los primeros cuatro momentos centrales (media, varianza, asimetría y exceso de curtosis). [1] [41] [42] El exceso de curtosis se expresó en términos del cuadrado de la asimetría y el tamaño de la muestra ν = α + β, (ver sección anterior "Curtosis") de la siguiente manera:
Se puede utilizar esta ecuación para resolver el tamaño de la muestra ν = α + β en términos del cuadrado de la asimetría y el exceso de curtosis de la siguiente manera: [41]
Esta es la relación (multiplicada por un factor de 3) entre los límites previamente derivados para la distribución beta en un espacio (como lo hizo originalmente Karl Pearson [20] ) definido con las coordenadas del cuadrado de la asimetría en un eje y el exceso de curtosis en el otro eje (ver § Curtosis limitada por el cuadrado de la asimetría):
El caso de asimetría cero, se puede resolver inmediatamente porque para asimetría cero, α = β y por lo tanto ν = 2α = 2β, por lo tanto α = β = ν/2
(El exceso de curtosis es negativo para la distribución beta con asimetría cero, que va de -2 a 0, de modo que -y por lo tanto los parámetros de forma de la muestra- es positivo, y va de cero cuando los parámetros de forma se aproximan a cero y el exceso de curtosis se aproxima a -2, hasta infinito cuando los parámetros de forma se aproximan a infinito y el exceso de curtosis se aproxima a cero).
Para una asimetría de muestra distinta de cero, es necesario resolver un sistema de dos ecuaciones acopladas. Dado que la asimetría y el exceso de curtosis son independientes de los parámetros , estos pueden determinarse de forma única a partir de la asimetría de muestra y el exceso de curtosis de muestra, resolviendo las ecuaciones acopladas con dos variables conocidas (asimetría de muestra y exceso de curtosis de muestra) y dos incógnitas (los parámetros de forma):
resultando en la siguiente solución: [41]
Donde se deben tomar las soluciones como sigue: para asimetría de muestra (negativa) < 0, y para asimetría de muestra (positiva) > 0.
El gráfico adjunto muestra estas dos soluciones como superficies en un espacio con ejes horizontales de (exceso de curtosis de la muestra) y (asimetría al cuadrado de la muestra) y los parámetros de forma como el eje vertical. Las superficies están restringidas por la condición de que el exceso de curtosis de la muestra debe estar limitado por la asimetría al cuadrado de la muestra como se estipula en la ecuación anterior. Las dos superficies se encuentran en el borde derecho definido por la asimetría cero. A lo largo de este borde derecho, ambos parámetros son iguales y la distribución es simétrica en forma de U para α = β < 1, uniforme para α = β = 1, en forma de U invertida para 1 < α = β < 2 y en forma de campana para α = β > 2. Las superficies también se encuentran en el borde frontal (inferior) definido por la línea del "límite imposible" (exceso de curtosis + 2 - asimetría 2 = 0). A lo largo de este límite frontal (inferior), ambos parámetros de forma se aproximan a cero, y la densidad de probabilidad se concentra más en un extremo que en el otro (prácticamente sin nada en el medio), con probabilidades en el extremo izquierdo x = 0 y en el extremo derecho x = 1. Las dos superficies se separan aún más hacia el borde posterior. En este borde posterior, los parámetros de superficie son bastante diferentes entre sí. Como observaron, por ejemplo, Bowman y Shenton, [43] el muestreo en la vecindad de la línea (exceso de curtosis de la muestra - (3/2)(asimetría de la muestra) 2 = 0) (la porción en forma de J del borde posterior donde el azul se encuentra con el beige), "está peligrosamente cerca del caos", porque en esa línea el denominador de la expresión anterior para la estimación ν = α + β se vuelve cero y, por lo tanto, ν se acerca al infinito a medida que se aproxima a esa línea. Bowman y Shenton [43] escriben que "los parámetros de momento más altos (curtosis y asimetría) son extremadamente frágiles (cerca de esa línea). Sin embargo, la media y la desviación estándar son bastante fiables". Por lo tanto, el problema es para el caso de estimación de cuatro parámetros para distribuciones muy asimétricas tales que el exceso de curtosis se acerca a (3/2) veces el cuadrado de la asimetría. Esta línea límite se produce por distribuciones extremadamente asimétricas con valores muy grandes de uno de los parámetros y valores muy pequeños del otro parámetro. Véase § Curtosis limitada por el cuadrado de la asimetría para un ejemplo numérico y más comentarios sobre esta línea límite del borde posterior (exceso de curtosis de la muestra - (3/2)(asimetría de la muestra) 2 = 0). Como señaló el propio Karl Pearson [44], este problema puede no tener mucha importancia práctica ya que este problema surge solo para distribuciones en forma de J muy asimétricas (o en forma de J imagen especular) con valores muy diferentes de parámetros de forma que es poco probable que ocurran mucho en la práctica). Las distribuciones habituales en forma de campana sesgada que ocurren en la práctica no tienen este problema de estimación de parámetros.
Los dos parámetros restantes se pueden determinar utilizando la media de la muestra y la varianza de la muestra utilizando una variedad de ecuaciones. [1] [41] Una alternativa es calcular el rango del intervalo de soporte en función de la varianza de la muestra y la curtosis de la muestra. Para este propósito se puede resolver, en términos del rango , la ecuación que expresa el exceso de curtosis en términos de la varianza de la muestra y el tamaño de la muestra ν (ver § Curtosis y § Parametrizaciones alternativas, cuatro parámetros):
Para obtener:
Otra alternativa es calcular el rango del intervalo de soporte en función de la varianza de la muestra y la asimetría de la muestra. [41] Para este propósito se puede resolver, en términos del rango , la ecuación que expresa la asimetría al cuadrado en términos de la varianza de la muestra y el tamaño de la muestra ν (ver la sección titulada "Asimetría" y "Parametrizaciones alternativas, cuatro parámetros"):
para obtener: [41]
El parámetro restante se puede determinar a partir de la media de la muestra y los parámetros obtenidos previamente :
y por último, .
En las fórmulas anteriores se pueden tomar, por ejemplo, como estimaciones de los momentos muestrales:
Los estimadores G 1 para asimetría de la muestra y G 2 para curtosis de la muestra son utilizados por DAP / SAS , PSPP / SPSS y Excel . Sin embargo, no son utilizados por BMDP y (según [45] ) no fueron utilizados por MINITAB en 1998. En realidad, Joanes y Gill en su estudio de 1998 [45] concluyeron que los estimadores de asimetría y curtosis utilizados en BMDP y en MINITAB (en ese momento) tenían menor varianza y error cuadrático medio en muestras normales, pero los estimadores de asimetría y curtosis utilizados en DAP / SAS , PSPP / SPSS , a saber, G 1 y G 2 , tenían menor error cuadrático medio en muestras de una distribución muy sesgada. Es por esta razón que hemos explicado "asimetría de la muestra", etc., en las fórmulas anteriores, para dejar explícito que el usuario debe elegir el mejor estimador según el problema en cuestión, ya que el mejor estimador para asimetría y curtosis depende de la cantidad de asimetría (como lo muestran Joanes y Gill [45] ).
Máxima verosimilitud
Dos parámetros desconocidos

Como también es el caso de las estimaciones de máxima verosimilitud para la distribución gamma , las estimaciones de máxima verosimilitud para la distribución beta no tienen una solución general de forma cerrada para valores arbitrarios de los parámetros de forma. Si X 1 , ..., X N son variables aleatorias independientes que tienen cada una una distribución beta, la función de verosimilitud conjunta para N observaciones iid es:
Para encontrar el máximo con respecto a un parámetro de forma es necesario tomar la derivada parcial con respecto al parámetro de forma y establecer la expresión igual a cero, obteniendo así el estimador de máxima verosimilitud de los parámetros de forma:
dónde:
ya que la función digamma denotada ψ(α) se define como la derivada logarítmica de la función gamma : [17]
Para garantizar que los valores con pendiente tangente cero sean de hecho un máximo (en lugar de un punto de silla o un mínimo), también hay que satisfacer la condición de que la curvatura sea negativa. Esto equivale a satisfacer que la segunda derivada parcial con respecto a los parámetros de forma sea negativa.
Usando las ecuaciones anteriores, esto es equivalente a:
donde la función trigamma , denotada ψ 1 ( α ), es la segunda de las funciones poligamma , y se define como la derivada de la función digamma :
Estas condiciones equivalen a afirmar que las varianzas de las variables transformadas logarítmicamente son positivas, ya que:
Por lo tanto, la condición de curvatura negativa en un máximo es equivalente a las afirmaciones:
Alternativamente, la condición de curvatura negativa en un máximo también es equivalente a afirmar que las siguientes derivadas logarítmicas de las medias geométricas G X y G (1−X) son positivas, ya que:
Si bien estas pendientes son efectivamente positivas, las otras pendientes son negativas:
Las pendientes de la media y la mediana con respecto a α y β muestran un comportamiento de signo similar.
A partir de la condición de que, como máximo, la derivada parcial con respecto al parámetro de forma es igual a cero, obtenemos el siguiente sistema de ecuaciones de estimación de máxima verosimilitud acopladas (para las verosimilitudes medias) que deben invertirse para obtener las estimaciones (desconocidas) del parámetro de forma en términos del promedio (conocido) de los logaritmos de las muestras X 1 , ..., X N : [1]
donde reconocemos como el logaritmo de la media geométrica de la muestra y como el logaritmo de la media geométrica de la muestra basada en (1 − X ), la imagen especular de X . Para , se sigue que .
Estas ecuaciones acopladas que contienen funciones digamma de las estimaciones de los parámetros de forma deben resolverse mediante métodos numéricos como lo hacen, por ejemplo, Beckman et al. [46] Gnanadesikan et al. ofrecen soluciones numéricas para algunos casos. [47] NLJohnson y S.Kotz [1] sugieren que para estimaciones de parámetros de forma "no demasiado pequeñas" , se puede utilizar la aproximación logarítmica a la función digamma para obtener valores iniciales para una solución iterativa, ya que las ecuaciones resultantes de esta aproximación se pueden resolver exactamente:
lo que conduce a la siguiente solución para los valores iniciales (de los parámetros de forma estimados en términos de las medias geométricas de la muestra) para una solución iterativa:
Alternativamente, las estimaciones proporcionadas por el método de momentos se pueden utilizar como valores iniciales para una solución iterativa de las ecuaciones acopladas de máxima verosimilitud en términos de las funciones digamma.
Cuando se requiere la distribución sobre un intervalo conocido distinto de [0, 1] con la variable aleatoria X , digamos [ a , c ] con la variable aleatoria Y , entonces reemplace ln( X i ) en la primera ecuación con
- ,
y reemplaza ln(1− X i ) en la segunda ecuación con
(ver sección “Parametrizaciones alternativas, cuatro parámetros” más abajo).
Si se conoce uno de los parámetros de forma, el problema se simplifica considerablemente. Se puede utilizar la siguiente transformación logit para resolver el parámetro de forma desconocido (para casos sesgados tales que , de lo contrario, si es simétrico, se conocen ambos parámetros -iguales- cuando se conoce uno):
Esta transformación logit es el logaritmo de la transformación que divide la variable X por su imagen especular ( X /(1 - X ) resultando en la "distribución beta invertida" o distribución beta prima (también conocida como distribución beta de segundo tipo o Tipo VI de Pearson ) con soporte [0, +∞). Como se discutió previamente en la sección "Momentos de variables aleatorias transformadas logarítmicamente", la transformación logit , estudiada por Johnson, [24] extiende el soporte finito [0, 1] basado en la variable original X a un soporte infinito en ambas direcciones de la línea real (−∞, +∞).
Si, por ejemplo, se conoce, el parámetro desconocido se puede obtener en términos de la función digamma inversa [48] del lado derecho de esta ecuación:
En particular, si uno de los parámetros de forma tiene un valor de unidad, por ejemplo para (la distribución de función de potencia con soporte acotado [0,1]), utilizando la identidad ψ( x + 1) = ψ( x ) + 1/ x en la ecuación , el estimador de máxima verosimilitud para el parámetro desconocido es, [1] exactamente:
La beta tiene soporte [0, 1], por lo tanto , y por lo tanto , y por lo tanto
In conclusion, the maximum likelihood estimates of the shape parameters of a beta distribution are (in general) a complicated function of the sample geometric mean, and of the sample geometric mean based on (1−X), the mirror-image of X. One may ask, if the variance (in addition to the mean) is necessary to estimate two shape parameters with the method of moments, why is the (logarithmic or geometric) variance not necessary to estimate two shape parameters with the maximum likelihood method, for which only the geometric means suffice? The answer is because the mean does not provide as much information as the geometric mean. For a beta distribution with equal shape parameters α = β, the mean is exactly 1/2, regardless of the value of the shape parameters, and therefore regardless of the value of the statistical dispersion (the variance). On the other hand, the geometric mean of a beta distribution with equal shape parameters α = β, depends on the value of the shape parameters, and therefore it contains more information. Also, the geometric mean of a beta distribution does not satisfy the symmetry conditions satisfied by the mean, therefore, by employing both the geometric mean based on X and geometric mean based on (1 − X), the maximum likelihood method is able to provide best estimates for both parameters α = β, without need of employing the variance.
One can express the joint log likelihood per N iid observations in terms of the sufficient statistics (the sample geometric means) as follows:
We can plot the joint log likelihood per N observations for fixed values of the sample geometric means to see the behavior of the likelihood function as a function of the shape parameters α and β. In such a plot, the shape parameter estimators correspond to the maxima of the likelihood function. See the accompanying graph that shows that all the likelihood functions intersect at α = β = 1, which corresponds to the values of the shape parameters that give the maximum entropy (the maximum entropy occurs for shape parameters equal to unity: the uniform distribution). It is evident from the plot that the likelihood function gives sharp peaks for values of the shape parameter estimators close to zero, but that for values of the shape parameters estimators greater than one, the likelihood function becomes quite flat, with less defined peaks. Obviously, the maximum likelihood parameter estimation method for the beta distribution becomes less acceptable for larger values of the shape parameter estimators, as the uncertainty in the peak definition increases with the value of the shape parameter estimators. One can arrive at the same conclusion by noticing that the expression for the curvature of the likelihood function is in terms of the geometric variances
These variances (and therefore the curvatures) are much larger for small values of the shape parameter α and β. However, for shape parameter values α, β > 1, the variances (and therefore the curvatures) flatten out. Equivalently, this result follows from the Cramér–Rao bound, since the Fisher information matrix components for the beta distribution are these logarithmic variances. The Cramér–Rao bound states that the variance of any unbiased estimator of α is bounded by the reciprocal of the Fisher information:
so the variance of the estimators increases with increasing α and β, as the logarithmic variances decrease.
Also one can express the joint log likelihood per N iid observations in terms of the digamma function expressions for the logarithms of the sample geometric means as follows:
this expression is identical to the negative of the cross-entropy (see section on "Quantities of information (entropy)"). Therefore, finding the maximum of the joint log likelihood of the shape parameters, per N iid observations, is identical to finding the minimum of the cross-entropy for the beta distribution, as a function of the shape parameters.
with the cross-entropy defined as follows:
Four unknown parameters
The procedure is similar to the one followed in the two unknown parameter case. If Y1, ..., YN are independent random variables each having a beta distribution with four parameters, the joint log likelihood function for N iid observations is:
Finding the maximum with respect to a shape parameter involves taking the partial derivative with respect to the shape parameter and setting the expression equal to zero yielding the maximum likelihood estimator of the shape parameters:
these equations can be re-arranged as the following system of four coupled equations (the first two equations are geometric means and the second two equations are the harmonic means) in terms of the maximum likelihood estimates for the four parameters :
with sample geometric means:
The parameters are embedded inside the geometric mean expressions in a nonlinear way (to the power 1/N). This precludes, in general, a closed form solution, even for an initial value approximation for iteration purposes. One alternative is to use as initial values for iteration the values obtained from the method of moments solution for the four parameter case. Furthermore, the expressions for the harmonic means are well-defined only for , which precludes a maximum likelihood solution for shape parameters less than unity in the four-parameter case. Fisher's information matrix for the four parameter case is positive-definite only for α, β > 2 (for further discussion, see section on Fisher information matrix, four parameter case), for bell-shaped (symmetric or unsymmetric) beta distributions, with inflection points located to either side of the mode. The following Fisher information components (that represent the expectations of the curvature of the log likelihood function) have singularities at the following values:
(for further discussion see section on Fisher information matrix). Thus, it is not possible to strictly carry on the maximum likelihood estimation for some well known distributions belonging to the four-parameter beta distribution family, like the uniform distribution (Beta(1, 1, a, c)), and the arcsine distribution (Beta(1/2, 1/2, a, c)). N.L.Johnson and S.Kotz[1] ignore the equations for the harmonic means and instead suggest "If a and c are unknown, and maximum likelihood estimators of a, c, α and β are required, the above procedure (for the two unknown parameter case, with X transformed as X = (Y − a)/(c − a)) can be repeated using a succession of trial values of a and c, until the pair (a, c) for which maximum likelihood (given a and c) is as great as possible, is attained" (where, for the purpose of clarity, their notation for the parameters has been translated into the present notation).
Fisher information matrix
Let a random variable X have a probability density f(x;α). The partial derivative with respect to the (unknown, and to be estimated) parameter α of the log likelihood function is called the score. The second moment of the score is called the Fisher information:
The expectation of the score is zero, therefore the Fisher information is also the second moment centered on the mean of the score: the variance of the score.
If the log likelihood function is twice differentiable with respect to the parameter α, and under certain regularity conditions,[49] then the Fisher information may also be written as follows (which is often a more convenient form for calculation purposes):
Thus, the Fisher information is the negative of the expectation of the second derivative with respect to the parameter α of the log likelihood function. Therefore, Fisher information is a measure of the curvature of the log likelihood function of α. A low curvature (and therefore high radius of curvature), flatter log likelihood function curve has low Fisher information; while a log likelihood function curve with large curvature (and therefore low radius of curvature) has high Fisher information. When the Fisher information matrix is computed at the evaluates of the parameters ("the observed Fisher information matrix") it is equivalent to the replacement of the true log likelihood surface by a Taylor's series approximation, taken as far as the quadratic terms.[50] The word information, in the context of Fisher information, refers to information about the parameters. Information such as: estimation, sufficiency and properties of variances of estimators. The Cramér–Rao bound states that the inverse of the Fisher information is a lower bound on the variance of any estimator of a parameter α:
The precision to which one can estimate the estimator of a parameter α is limited by the Fisher Information of the log likelihood function. The Fisher information is a measure of the minimum error involved in estimating a parameter of a distribution and it can be viewed as a measure of the resolving power of an experiment needed to discriminate between two alternative hypothesis of a parameter.[51]
When there are N parameters
then the Fisher information takes the form of an N×N positive semidefinite symmetric matrix, the Fisher information matrix, with typical element:
Under certain regularity conditions,[49] the Fisher Information Matrix may also be written in the following form, which is often more convenient for computation:
With X1, ..., XN iid random variables, an N-dimensional "box" can be constructed with sides X1, ..., XN. Costa and Cover[52] show that the (Shannon) differential entropy h(X) is related to the volume of the typical set (having the sample entropy close to the true entropy), while the Fisher information is related to the surface of this typical set.
Two parameters
For X1, ..., XN independent random variables each having a beta distribution parametrized with shape parameters α and β, the joint log likelihood function for N iid observations is:
therefore the joint log likelihood function per N iid observations is
For the two parameter case, the Fisher information has 4 components: 2 diagonal and 2 off-diagonal. Since the Fisher information matrix is symmetric, one of these off diagonal components is independent. Therefore, the Fisher information matrix has 3 independent components (2 diagonal and 1 off diagonal).
Aryal and Nadarajah[53] calculated Fisher's information matrix for the four-parameter case, from which the two parameter case can be obtained as follows:
Since the Fisher information matrix is symmetric
The Fisher information components are equal to the log geometric variances and log geometric covariance. Therefore, they can be expressed as trigamma functions, denoted ψ1(α), the second of the polygamma functions, defined as the derivative of the digamma function:
These derivatives are also derived in the § Two unknown parameters and plots of the log likelihood function are also shown in that section. § Geometric variance and covariance contains plots and further discussion of the Fisher information matrix components: the log geometric variances and log geometric covariance as a function of the shape parameters α and β. § Moments of logarithmically transformed random variables contains formulas for moments of logarithmically transformed random variables. Images for the Fisher information components and are shown in § Geometric variance.
The determinant of Fisher's information matrix is of interest (for example for the calculation of Jeffreys prior probability). From the expressions for the individual components of the Fisher information matrix, it follows that the determinant of Fisher's (symmetric) information matrix for the beta distribution is:
From Sylvester's criterion (checking whether the diagonal elements are all positive), it follows that the Fisher information matrix for the two parameter case is positive-definite (under the standard condition that the shape parameters are positive α > 0 and β > 0).
Four parameters


If Y1, ..., YN are independent random variables each having a beta distribution with four parameters: the exponents α and β, and also a (the minimum of the distribution range), and c (the maximum of the distribution range) (section titled "Alternative parametrizations", "Four parameters"), with probability density function:
the joint log likelihood function per N iid observations is:
For the four parameter case, the Fisher information has 4*4=16 components. It has 12 off-diagonal components = (4×4 total − 4 diagonal). Since the Fisher information matrix is symmetric, half of these components (12/2=6) are independent. Therefore, the Fisher information matrix has 6 independent off-diagonal + 4 diagonal = 10 independent components. Aryal and Nadarajah[53] calculated Fisher's information matrix for the four parameter case as follows:
In the above expressions, the use of X instead of Y in the expressions var[ln(X)] = ln(varGX) is not an error. The expressions in terms of the log geometric variances and log geometric covariance occur as functions of the two parameter X ~ Beta(α, β) parametrization because when taking the partial derivatives with respect to the exponents (α, β) in the four parameter case, one obtains the identical expressions as for the two parameter case: these terms of the four parameter Fisher information matrix are independent of the minimum a and maximum c of the distribution's range. The only non-zero term upon double differentiation of the log likelihood function with respect to the exponents α and β is the second derivative of the log of the beta function: ln(B(α, β)). This term is independent of the minimum a and maximum c of the distribution's range. Double differentiation of this term results in trigamma functions. The sections titled "Maximum likelihood", "Two unknown parameters" and "Four unknown parameters" also show this fact.
The Fisher information for N i.i.d. samples is N times the individual Fisher information (eq. 11.279, page 394 of Cover and Thomas[27]). (Aryal and Nadarajah[53] take a single observation, N = 1, to calculate the following components of the Fisher information, which leads to the same result as considering the derivatives of the log likelihood per N observations. Moreover, below the erroneous expression for in Aryal and Nadarajah has been corrected.)
The lower two diagonal entries of the Fisher information matrix, with respect to the parameter a (the minimum of the distribution's range): , and with respect to the parameter c (the maximum of the distribution's range): are only defined for exponents α > 2 and β > 2 respectively. The Fisher information matrix component for the minimum a approaches infinity for exponent α approaching 2 from above, and the Fisher information matrix component for the maximum c approaches infinity for exponent β approaching 2 from above.
The Fisher information matrix for the four parameter case does not depend on the individual values of the minimum a and the maximum c, but only on the total range (c − a). Moreover, the components of the Fisher information matrix that depend on the range (c − a), depend only through its inverse (or the square of the inverse), such that the Fisher information decreases for increasing range (c − a).
The accompanying images show the Fisher information components and . Images for the Fisher information components and are shown in § Geometric variance. All these Fisher information components look like a basin, with the "walls" of the basin being located at low values of the parameters.
The following four-parameter-beta-distribution Fisher information components can be expressed in terms of the two-parameter: X ~ Beta(α, β) expectations of the transformed ratio ((1 − X)/X) and of its mirror image (X/(1 − X)), scaled by the range (c − a), which may be helpful for interpretation:
These are also the expected values of the "inverted beta distribution" or beta prime distribution (also known as beta distribution of the second kind or Pearson's Type VI) [1] and its mirror image, scaled by the range (c − a).
Also, the following Fisher information components can be expressed in terms of the harmonic (1/X) variances or of variances based on the ratio transformed variables ((1-X)/X) as follows:
See section "Moments of linearly transformed, product and inverted random variables" for these expectations.
The determinant of Fisher's information matrix is of interest (for example for the calculation of Jeffreys prior probability). From the expressions for the individual components, it follows that the determinant of Fisher's (symmetric) information matrix for the beta distribution with four parameters is:
Using Sylvester's criterion (checking whether the diagonal elements are all positive), and since diagonal components and have singularities at α=2 and β=2 it follows that the Fisher information matrix for the four parameter case is positive-definite for α>2 and β>2. Since for α > 2 and β > 2 the beta distribution is (symmetric or unsymmetric) bell shaped, it follows that the Fisher information matrix is positive-definite only for bell-shaped (symmetric or unsymmetric) beta distributions, with inflection points located to either side of the mode. Thus, important well known distributions belonging to the four-parameter beta distribution family, like the parabolic distribution (Beta(2,2,a,c)) and the uniform distribution (Beta(1,1,a,c)) have Fisher information components () that blow up (approach infinity) in the four-parameter case (although their Fisher information components are all defined for the two parameter case). The four-parameter Wigner semicircle distribution (Beta(3/2,3/2,a,c)) and arcsine distribution (Beta(1/2,1/2,a,c)) have negative Fisher information determinants for the four-parameter case.
Bayesian inference

The use of Beta distributions in Bayesian inference is due to the fact that they provide a family of conjugate prior probability distributions for binomial (including Bernoulli) and geometric distributions. The domain of the beta distribution can be viewed as a probability, and in fact the beta distribution is often used to describe the distribution of a probability value p:[23]
Examples of beta distributions used as prior probabilities to represent ignorance of prior parameter values in Bayesian inference are Beta(1,1), Beta(0,0) and Beta(1/2,1/2).
Rule of succession
A classic application of the beta distribution is the rule of succession, introduced in the 18th century by Pierre-Simon Laplace[54] in the course of treating the sunrise problem. It states that, given s successes in n conditionally independent Bernoulli trials with probability p, that the estimate of the expected value in the next trial is . This estimate is the expected value of the posterior distribution over p, namely Beta(s+1, n−s+1), which is given by Bayes' rule if one assumes a uniform prior probability over p (i.e., Beta(1, 1)) and then observes that p generated s successes in n trials. Laplace's rule of succession has been criticized by prominent scientists. R. T. Cox described Laplace's application of the rule of succession to the sunrise problem ([55] p. 89) as "a travesty of the proper use of the principle". Keynes remarks ([56] Ch.XXX, p. 382) "indeed this is so foolish a theorem that to entertain it is discreditable". Karl Pearson[57] showed that the probability that the next (n + 1) trials will be successes, after n successes in n trials, is only 50%, which has been considered too low by scientists like Jeffreys and unacceptable as a representation of the scientific process of experimentation to test a proposed scientific law. As pointed out by Jeffreys ([58] p. 128) (crediting C. D. Broad[59] ) Laplace's rule of succession establishes a high probability of success ((n+1)/(n+2)) in the next trial, but only a moderate probability (50%) that a further sample (n+1) comparable in size will be equally successful. As pointed out by Perks,[60] "The rule of succession itself is hard to accept. It assigns a probability to the next trial which implies the assumption that the actual run observed is an average run and that we are always at the end of an average run. It would, one would think, be more reasonable to assume that we were in the middle of an average run. Clearly a higher value for both probabilities is necessary if they are to accord with reasonable belief." These problems with Laplace's rule of succession motivated Haldane, Perks, Jeffreys and others to search for other forms of prior probability (see the next § Bayesian inference). According to Jaynes,[51] the main problem with the rule of succession is that it is not valid when s=0 or s=n (see rule of succession, for an analysis of its validity).
Bayes–Laplace prior probability (Beta(1,1))
The beta distribution achieves maximum differential entropy for Beta(1,1): the uniform probability density, for which all values in the domain of the distribution have equal density. This uniform distribution Beta(1,1) was suggested ("with a great deal of doubt") by Thomas Bayes[61] as the prior probability distribution to express ignorance about the correct prior distribution. This prior distribution was adopted (apparently, from his writings, with little sign of doubt[54]) by Pierre-Simon Laplace, and hence it was also known as the "Bayes–Laplace rule" or the "Laplace rule" of "inverse probability" in publications of the first half of the 20th century. In the later part of the 19th century and early part of the 20th century, scientists realized that the assumption of uniform "equal" probability density depended on the actual functions (for example whether a linear or a logarithmic scale was most appropriate) and parametrizations used. In particular, the behavior near the ends of distributions with finite support (for example near x = 0, for a distribution with initial support at x = 0) required particular attention. Keynes ([56] Ch.XXX, p. 381) criticized the use of Bayes's uniform prior probability (Beta(1,1)) that all values between zero and one are equiprobable, as follows: "Thus experience, if it shows anything, shows that there is a very marked clustering of statistical ratios in the neighborhoods of zero and unity, of those for positive theories and for correlations between positive qualities in the neighborhood of zero, and of those for negative theories and for correlations between negative qualities in the neighborhood of unity. "
Haldane's prior probability (Beta(0,0))

The Beta(0,0) distribution was proposed by J.B.S. Haldane,[62] who suggested that the prior probability representing complete uncertainty should be proportional to p−1(1−p)−1. The function p−1(1−p)−1 can be viewed as the limit of the numerator of the beta distribution as both shape parameters approach zero: α, β → 0. The Beta function (in the denominator of the beta distribution) approaches infinity, for both parameters approaching zero, α, β → 0. Therefore, p−1(1−p)−1 divided by the Beta function approaches a 2-point Bernoulli distribution with equal probability 1/2 at each end, at 0 and 1, and nothing in between, as α, β → 0. A coin-toss: one face of the coin being at 0 and the other face being at 1. The Haldane prior probability distribution Beta(0,0) is an "improper prior" because its integration (from 0 to 1) fails to strictly converge to 1 due to the singularities at each end. However, this is not an issue for computing posterior probabilities unless the sample size is very small. Furthermore, Zellner[63] points out that on the log-odds scale, (the logit transformation ln(p/1 − p)), the Haldane prior is the uniformly flat prior. The fact that a uniform prior probability on the logit transformed variable ln(p/1 − p) (with domain (−∞, ∞)) is equivalent to the Haldane prior on the domain [0, 1] was pointed out by Harold Jeffreys in the first edition (1939) of his book Theory of Probability ([58] p. 123). Jeffreys writes "Certainly if we take the Bayes–Laplace rule right up to the extremes we are led to results that do not correspond to anybody's way of thinking. The (Haldane) rule dx/(x(1 − x)) goes too far the other way. It would lead to the conclusion that if a sample is of one type with respect to some property there is a probability 1 that the whole population is of that type." The fact that "uniform" depends on the parametrization, led Jeffreys to seek a form of prior that would be invariant under different parametrizations.
Jeffreys' prior probability (Beta(1/2,1/2) for a Bernoulli or for a binomial distribution)




Harold Jeffreys[58][64] proposed to use an uninformative prior probability measure that should be invariant under reparameterization: proportional to the square root of the determinant of Fisher's information matrix. For the Bernoulli distribution, this can be shown as follows: for a coin that is "heads" with probability p ∈ [0, 1] and is "tails" with probability 1 − p, for a given (H,T) ∈ {(0,1), (1,0)} the probability is pH(1 − p)T. Since T = 1 − H, the Bernoulli distribution is pH(1 − p)1 − H. Considering p as the only parameter, it follows that the log likelihood for the Bernoulli distribution is
The Fisher information matrix has only one component (it is a scalar, because there is only one parameter: p), therefore:
Similarly, for the Binomial distribution with n Bernoulli trials, it can be shown that
Thus, for the Bernoulli, and Binomial distributions, Jeffreys prior is proportional to , which happens to be proportional to a beta distribution with domain variable x = p, and shape parameters α = β = 1/2, the arcsine distribution:
It will be shown in the next section that the normalizing constant for Jeffreys prior is immaterial to the final result because the normalizing constant cancels out in Bayes theorem for the posterior probability. Hence Beta(1/2,1/2) is used as the Jeffreys prior for both Bernoulli and binomial distributions. As shown in the next section, when using this expression as a prior probability times the likelihood in Bayes theorem, the posterior probability turns out to be a beta distribution. It is important to realize, however, that Jeffreys prior is proportional to for the Bernoulli and binomial distribution, but not for the beta distribution. Jeffreys prior for the beta distribution is given by the determinant of Fisher's information for the beta distribution, which, as shown in the § Fisher information matrix is a function of the trigamma function ψ1 of shape parameters α and β as follows:
As previously discussed, Jeffreys prior for the Bernoulli and binomial distributions is proportional to the arcsine distribution Beta(1/2,1/2), a one-dimensional curve that looks like a basin as a function of the parameter p of the Bernoulli and binomial distributions. The walls of the basin are formed by p approaching the singularities at the ends p → 0 and p → 1, where Beta(1/2,1/2) approaches infinity. Jeffreys prior for the beta distribution is a 2-dimensional surface (embedded in a three-dimensional space) that looks like a basin with only two of its walls meeting at the corner α = β = 0 (and missing the other two walls) as a function of the shape parameters α and β of the beta distribution. The two adjoining walls of this 2-dimensional surface are formed by the shape parameters α and β approaching the singularities (of the trigamma function) at α, β → 0. It has no walls for α, β → ∞ because in this case the determinant of Fisher's information matrix for the beta distribution approaches zero.
It will be shown in the next section that Jeffreys prior probability results in posterior probabilities (when multiplied by the binomial likelihood function) that are intermediate between the posterior probability results of the Haldane and Bayes prior probabilities.
Jeffreys prior may be difficult to obtain analytically, and for some cases it just doesn't exist (even for simple distribution functions like the asymmetric triangular distribution). Berger, Bernardo and Sun, in a 2009 paper[65] defined a reference prior probability distribution that (unlike Jeffreys prior) exists for the asymmetric triangular distribution. They cannot obtain a closed-form expression for their reference prior, but numerical calculations show it to be nearly perfectly fitted by the (proper) prior
where θ is the vertex variable for the asymmetric triangular distribution with support [0, 1] (corresponding to the following parameter values in Wikipedia's article on the triangular distribution: vertex c = θ, left end a = 0,and right end b = 1). Berger et al. also give a heuristic argument that Beta(1/2,1/2) could indeed be the exact Berger–Bernardo–Sun reference prior for the asymmetric triangular distribution. Therefore, Beta(1/2,1/2) not only is Jeffreys prior for the Bernoulli and binomial distributions, but also seems to be the Berger–Bernardo–Sun reference prior for the asymmetric triangular distribution (for which the Jeffreys prior does not exist), a distribution used in project management and PERT analysis to describe the cost and duration of project tasks.
Clarke and Barron[66] prove that, among continuous positive priors, Jeffreys prior (when it exists) asymptotically maximizes Shannon's mutual information between a sample of size n and the parameter, and therefore Jeffreys prior is the most uninformative prior (measuring information as Shannon information). The proof rests on an examination of the Kullback–Leibler divergence between probability density functions for iid random variables.
Effect of different prior probability choices on the posterior beta distribution
If samples are drawn from the population of a random variable X that result in s successes and f failures in n Bernoulli trials n = s + f, then the likelihood function for parameters s and f given x = p (the notation x = p in the expressions below will emphasize that the domain x stands for the value of the parameter p in the binomial distribution), is the following binomial distribution:
If beliefs about prior probability information are reasonably well approximated by a beta distribution with parameters α Prior and β Prior, then:
According to Bayes' theorem for a continuous event space, the posterior probability density is given by the product of the prior probability and the likelihood function (given the evidence s and f = n − s), normalized so that the area under the curve equals one, as follows:
appears both in the numerator and the denominator of the posterior probability, and it does not depend on the integration variable x, hence it cancels out, and it is irrelevant to the final result. Similarly the normalizing factor for the prior probability, the beta function B(αPrior,βPrior) cancels out and it is immaterial to the final result. The same posterior probability result can be obtained if one uses an un-normalized prior
because the normalizing factors all cancel out. Several authors (including Jeffreys himself) thus use an un-normalized prior formula since the normalization constant cancels out. The numerator of the posterior probability ends up being just the (un-normalized) product of the prior probability and the likelihood function, and the denominator is its integral from zero to one. The beta function in the denominator, B(s + α Prior, n − s + β Prior), appears as a normalization constant to ensure that the total posterior probability integrates to unity.
The ratio s/n of the number of successes to the total number of trials is a sufficient statistic in the binomial case, which is relevant for the following results.
For the Bayes' prior probability (Beta(1,1)), the posterior probability is:
For the Jeffreys' prior probability (Beta(1/2,1/2)), the posterior probability is:
and for the Haldane prior probability (Beta(0,0)), the posterior probability is:
From the above expressions it follows that for s/n = 1/2) all the above three prior probabilities result in the identical location for the posterior probability mean = mode = 1/2. For s/n < 1/2, the mean of the posterior probabilities, using the following priors, are such that: mean for Bayes prior > mean for Jeffreys prior > mean for Haldane prior. For s/n > 1/2 the order of these inequalities is reversed such that the Haldane prior probability results in the largest posterior mean. The Haldane prior probability Beta(0,0) results in a posterior probability density with mean (the expected value for the probability of success in the "next" trial) identical to the ratio s/n of the number of successes to the total number of trials. Therefore, the Haldane prior results in a posterior probability with expected value in the next trial equal to the maximum likelihood. The Bayes prior probability Beta(1,1) results in a posterior probability density with mode identical to the ratio s/n (the maximum likelihood).
In the case that 100% of the trials have been successful s = n, the Bayes prior probability Beta(1,1) results in a posterior expected value equal to the rule of succession (n + 1)/(n + 2), while the Haldane prior Beta(0,0) results in a posterior expected value of 1 (absolute certainty of success in the next trial). Jeffreys prior probability results in a posterior expected value equal to (n + 1/2)/(n + 1). Perks[60] (p. 303) points out: "This provides a new rule of succession and expresses a 'reasonable' position to take up, namely, that after an unbroken run of n successes we assume a probability for the next trial equivalent to the assumption that we are about half-way through an average run, i.e. that we expect a failure once in (2n + 2) trials. The Bayes–Laplace rule implies that we are about at the end of an average run or that we expect a failure once in (n + 2) trials. The comparison clearly favours the new result (what is now called Jeffreys prior) from the point of view of 'reasonableness'."
Conversely, in the case that 100% of the trials have resulted in failure (s = 0), the Bayes prior probability Beta(1,1) results in a posterior expected value for success in the next trial equal to 1/(n + 2), while the Haldane prior Beta(0,0) results in a posterior expected value of success in the next trial of 0 (absolute certainty of failure in the next trial). Jeffreys prior probability results in a posterior expected value for success in the next trial equal to (1/2)/(n + 1), which Perks[60] (p. 303) points out: "is a much more reasonably remote result than the Bayes–Laplace result 1/(n + 2)".
Jaynes[51] questions (for the uniform prior Beta(1,1)) the use of these formulas for the cases s = 0 or s = n because the integrals do not converge (Beta(1,1) is an improper prior for s = 0 or s = n). In practice, the conditions 0<s<n necessary for a mode to exist between both ends for the Bayes prior are usually met, and therefore the Bayes prior (as long as 0 < s < n) results in a posterior mode located between both ends of the domain.
As remarked in the section on the rule of succession, K. Pearson showed that after n successes in n trials the posterior probability (based on the Bayes Beta(1,1) distribution as the prior probability) that the next (n + 1) trials will all be successes is exactly 1/2, whatever the value of n. Based on the Haldane Beta(0,0) distribution as the prior probability, this posterior probability is 1 (absolute certainty that after n successes in n trials the next (n + 1) trials will all be successes). Perks[60] (p. 303) shows that, for what is now known as the Jeffreys prior, this probability is ((n + 1/2)/(n + 1))((n + 3/2)/(n + 2))...(2n + 1/2)/(2n + 1), which for n = 1, 2, 3 gives 15/24, 315/480, 9009/13440; rapidly approaching a limiting value of as n tends to infinity. Perks remarks that what is now known as the Jeffreys prior: "is clearly more 'reasonable' than either the Bayes–Laplace result or the result on the (Haldane) alternative rule rejected by Jeffreys which gives certainty as the probability. It clearly provides a very much better correspondence with the process of induction. Whether it is 'absolutely' reasonable for the purpose, i.e. whether it is yet large enough, without the absurdity of reaching unity, is a matter for others to decide. But it must be realized that the result depends on the assumption of complete indifference and absence of knowledge prior to the sampling experiment."
Following are the variances of the posterior distribution obtained with these three prior probability distributions:
for the Bayes' prior probability (Beta(1,1)), the posterior variance is:
for the Jeffreys' prior probability (Beta(1/2,1/2)), the posterior variance is:
and for the Haldane prior probability (Beta(0,0)), the posterior variance is:
So, as remarked by Silvey,[49] for large n, the variance is small and hence the posterior distribution is highly concentrated, whereas the assumed prior distribution was very diffuse. This is in accord with what one would hope for, as vague prior knowledge is transformed (through Bayes theorem) into a more precise posterior knowledge by an informative experiment. For small n the Haldane Beta(0,0) prior results in the largest posterior variance while the Bayes Beta(1,1) prior results in the more concentrated posterior. Jeffreys prior Beta(1/2,1/2) results in a posterior variance in between the other two. As n increases, the variance rapidly decreases so that the posterior variance for all three priors converges to approximately the same value (approaching zero variance as n → ∞). Recalling the previous result that the Haldane prior probability Beta(0,0) results in a posterior probability density with mean (the expected value for the probability of success in the "next" trial) identical to the ratio s/n of the number of successes to the total number of trials, it follows from the above expression that also the Haldane prior Beta(0,0) results in a posterior with variance identical to the variance expressed in terms of the max. likelihood estimate s/n and sample size (in § Variance):
with the mean μ = s/n and the sample size ν = n.
In Bayesian inference, using a prior distribution Beta(αPrior,βPrior) prior to a binomial distribution is equivalent to adding (αPrior − 1) pseudo-observations of "success" and (βPrior − 1) pseudo-observations of "failure" to the actual number of successes and failures observed, then estimating the parameter p of the binomial distribution by the proportion of successes over both real- and pseudo-observations. A uniform prior Beta(1,1) does not add (or subtract) any pseudo-observations since for Beta(1,1) it follows that (αPrior − 1) = 0 and (βPrior − 1) = 0. The Haldane prior Beta(0,0) subtracts one pseudo observation from each and Jeffreys prior Beta(1/2,1/2) subtracts 1/2 pseudo-observation of success and an equal number of failure. This subtraction has the effect of smoothing out the posterior distribution. If the proportion of successes is not 50% (s/n ≠ 1/2) values of αPrior and βPrior less than 1 (and therefore negative (αPrior − 1) and (βPrior − 1)) favor sparsity, i.e. distributions where the parameter p is closer to either 0 or 1. In effect, values of αPrior and βPrior between 0 and 1, when operating together, function as a concentration parameter.
The accompanying plots show the posterior probability density functions for sample sizes n ∈ {3,10,50}, successes s ∈ {n/2,n/4} and Beta(αPrior,βPrior) ∈ {Beta(0,0),Beta(1/2,1/2),Beta(1,1)}. Also shown are the cases for n = {4,12,40}, success s = {n/4} and Beta(αPrior,βPrior) ∈ {Beta(0,0),Beta(1/2,1/2),Beta(1,1)}. The first plot shows the symmetric cases, for successes s ∈ {n/2}, with mean = mode = 1/2 and the second plot shows the skewed cases s ∈ {n/4}. The images show that there is little difference between the priors for the posterior with sample size of 50 (characterized by a more pronounced peak near p = 1/2). Significant differences appear for very small sample sizes (in particular for the flatter distribution for the degenerate case of sample size = 3). Therefore, the skewed cases, with successes s = {n/4}, show a larger effect from the choice of prior, at small sample size, than the symmetric cases. For symmetric distributions, the Bayes prior Beta(1,1) results in the most "peaky" and highest posterior distributions and the Haldane prior Beta(0,0) results in the flattest and lowest peak distribution. The Jeffreys prior Beta(1/2,1/2) lies in between them. For nearly symmetric, not too skewed distributions the effect of the priors is similar. For very small sample size (in this case for a sample size of 3) and skewed distribution (in this example for s ∈ {n/4}) the Haldane prior can result in a reverse-J-shaped distribution with a singularity at the left end. However, this happens only in degenerate cases (in this example n = 3 and hence s = 3/4 < 1, a degenerate value because s should be greater than unity in order for the posterior of the Haldane prior to have a mode located between the ends, and because s = 3/4 is not an integer number, hence it violates the initial assumption of a binomial distribution for the likelihood) and it is not an issue in generic cases of reasonable sample size (such that the condition 1 < s < n − 1, necessary for a mode to exist between both ends, is fulfilled).
In Chapter 12 (p. 385) of his book, Jaynes[51] asserts that the Haldane prior Beta(0,0) describes a prior state of knowledge of complete ignorance, where we are not even sure whether it is physically possible for an experiment to yield either a success or a failure, while the Bayes (uniform) prior Beta(1,1) applies if one knows that both binary outcomes are possible. Jaynes states: "interpret the Bayes–Laplace (Beta(1,1)) prior as describing not a state of complete ignorance, but the state of knowledge in which we have observed one success and one failure...once we have seen at least one success and one failure, then we know that the experiment is a true binary one, in the sense of physical possibility." Jaynes [51] does not specifically discuss Jeffreys prior Beta(1/2,1/2) (Jaynes discussion of "Jeffreys prior" on pp. 181, 423 and on chapter 12 of Jaynes book[51] refers instead to the improper, un-normalized, prior "1/p dp" introduced by Jeffreys in the 1939 edition of his book,[58] seven years before he introduced what is now known as Jeffreys' invariant prior: the square root of the determinant of Fisher's information matrix. "1/p" is Jeffreys' (1946) invariant prior for the exponential distribution, not for the Bernoulli or binomial distributions). However, it follows from the above discussion that Jeffreys Beta(1/2,1/2) prior represents a state of knowledge in between the Haldane Beta(0,0) and Bayes Beta (1,1) prior.
Similarly, Karl Pearson in his 1892 book The Grammar of Science[67][68] (p. 144 of 1900 edition) maintained that the Bayes (Beta(1,1) uniform prior was not a complete ignorance prior, and that it should be used when prior information justified to "distribute our ignorance equally"". K. Pearson wrote: "Yet the only supposition that we appear to have made is this: that, knowing nothing of nature, routine and anomy (from the Greek ανομία, namely: a- "without", and nomos "law") are to be considered as equally likely to occur. Now we were not really justified in making even this assumption, for it involves a knowledge that we do not possess regarding nature. We use our experience of the constitution and action of coins in general to assert that heads and tails are equally probable, but we have no right to assert before experience that, as we know nothing of nature, routine and breach are equally probable. In our ignorance we ought to consider before experience that nature may consist of all routines, all anomies (normlessness), or a mixture of the two in any proportion whatever, and that all such are equally probable. Which of these constitutions after experience is the most probable must clearly depend on what that experience has been like."
If there is sufficient sampling data, and the posterior probability mode is not located at one of the extremes of the domain (x = 0 or x = 1), the three priors of Bayes (Beta(1,1)), Jeffreys (Beta(1/2,1/2)) and Haldane (Beta(0,0)) should yield similar posterior probability densities. Otherwise, as Gelman et al.[69] (p. 65) point out, "if so few data are available that the choice of noninformative prior distribution makes a difference, one should put relevant information into the prior distribution", or as Berger[4] (p. 125) points out "when different reasonable priors yield substantially different answers, can it be right to state that there is a single answer? Would it not be better to admit that there is scientific uncertainty, with the conclusion depending on prior beliefs?."
Occurrence and applications
Order statistics
The beta distribution has an important application in the theory of order statistics. A basic result is that the distribution of the kth smallest of a sample of size n from a continuous uniform distribution has a beta distribution.[38] This result is summarized as:
From this, and application of the theory related to the probability integral transform, the distribution of any individual order statistic from any continuous distribution can be derived.[38]
Subjective logic
In standard logic, propositions are considered to be either true or false. In contradistinction, subjective logic assumes that humans cannot determine with absolute certainty whether a proposition about the real world is absolutely true or false. In subjective logic the posteriori probability estimates of binary events can be represented by beta distributions.[70]
Wavelet analysis
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" that promptly decays. Wavelets can be used to extract information from many different kinds of data, including – but certainly not limited to – audio signals and images. Thus, wavelets are purposefully crafted to have specific properties that make them useful for signal processing. Wavelets are localized in both time and frequency whereas the standard Fourier transform is only localized in frequency. Therefore, standard Fourier Transforms are only applicable to stationary processes, while wavelets are applicable to non-stationary processes. Continuous wavelets can be constructed based on the beta distribution. Beta wavelets[71] can be viewed as a soft variety of Haar wavelets whose shape is fine-tuned by two shape parameters α and β.
Population genetics
The Balding–Nichols model is a two-parameter parametrization of the beta distribution used in population genetics.[72] It is a statistical description of the allele frequencies in the components of a sub-divided population:
where and ; here F is (Wright's) genetic distance between two populations.
Project management: task cost and schedule modeling
The beta distribution can be used to model events which are constrained to take place within an interval defined by a minimum and maximum value. For this reason, the beta distribution — along with the triangular distribution — is used extensively in PERT, critical path method (CPM), Joint Cost Schedule Modeling (JCSM) and other project management/control systems to describe the time to completion and the cost of a task. In project management, shorthand computations are widely used to estimate the mean and standard deviation of the beta distribution:[37]
where a is the minimum, c is the maximum, and b is the most likely value (the mode for α > 1 and β > 1).
The above estimate for the mean is known as the PERT three-point estimation and it is exact for either of the following values of β (for arbitrary α within these ranges):
- β = α > 1 (symmetric case) with standard deviation , skewness = 0, and excess kurtosis =
or
- β = 6 − α for 5 > α > 1 (skewed case) with standard deviation
skewness, and excess kurtosis
The above estimate for the standard deviation σ(X) = (c − a)/6 is exact for either of the following values of α and β:
- α = β = 4 (symmetric) with skewness = 0, and excess kurtosis = −6/11.
- β = 6 − α and (right-tailed, positive skew) with skewness, and excess kurtosis = 0
- β = 6 − α and (left-tailed, negative skew) with skewness, and excess kurtosis = 0
Otherwise, these can be poor approximations for beta distributions with other values of α and β, exhibiting average errors of 40% in the mean and 549% in the variance.[73][74][75]
Random variate generation
If X and Y are independent, with and then
So one algorithm for generating beta variates is to generate , where X is a gamma variate with parameters (α, 1) and Y is an independent gamma variate with parameters (β, 1).[76] In fact, here and are independent, and . If and is independent of and , then and is independent of . This shows that the product of independent and random variables is a random variable.
Also, the kth order statistic of n uniformly distributed variates is , so an alternative if α and β are small integers is to generate α + β − 1 uniform variates and choose the α-th smallest.[38]
Another way to generate the Beta distribution is by Pólya urn model. According to this method, one start with an "urn" with α "black" balls and β "white" balls and draw uniformly with replacement. Every trial an additional ball is added according to the color of the last ball which was drawn. Asymptotically, the proportion of black and white balls will be distributed according to the Beta distribution, where each repetition of the experiment will produce a different value.
It is also possible to use the inverse transform sampling.
Normal approximation to the Beta distribution
A beta distribution with α ~ β and α and β >> 1 is approximately normal with mean 1/2 and variance 1/(4(2α + 1)). If α ≥ β the normal approximation can be improved by taking the cube-root of the logarithm of the reciprocal of [77]
History
Thomas Bayes, in a posthumous paper [61] published in 1763 by Richard Price, obtained a beta distribution as the density of the probability of success in Bernoulli trials (see § Applications, Bayesian inference), but the paper does not analyze any of the moments of the beta distribution or discuss any of its properties.

The first systematic modern discussion of the beta distribution is probably due to Karl Pearson.[78][79] In Pearson's papers[20][32] the beta distribution is couched as a solution of a differential equation: Pearson's Type I distribution which it is essentially identical to except for arbitrary shifting and re-scaling (the beta and Pearson Type I distributions can always be equalized by proper choice of parameters). In fact, in several English books and journal articles in the few decades prior to World War II, it was common to refer to the beta distribution as Pearson's Type I distribution. William P. Elderton in his 1906 monograph "Frequency curves and correlation"[41] further analyzes the beta distribution as Pearson's Type I distribution, including a full discussion of the method of moments for the four parameter case, and diagrams of (what Elderton describes as) U-shaped, J-shaped, twisted J-shaped, "cocked-hat" shapes, horizontal and angled straight-line cases. Elderton wrote "I am chiefly indebted to Professor Pearson, but the indebtedness is of a kind for which it is impossible to offer formal thanks." Elderton in his 1906 monograph [41] provides an impressive amount of information on the beta distribution, including equations for the origin of the distribution chosen to be the mode, as well as for other Pearson distributions: types I through VII. Elderton also included a number of appendixes, including one appendix ("II") on the beta and gamma functions. In later editions, Elderton added equations for the origin of the distribution chosen to be the mean, and analysis of Pearson distributions VIII through XII.
As remarked by Bowman and Shenton[43] "Fisher and Pearson had a difference of opinion in the approach to (parameter) estimation, in particular relating to (Pearson's method of) moments and (Fisher's method of) maximum likelihood in the case of the Beta distribution." Also according to Bowman and Shenton, "the case of a Type I (beta distribution) model being the center of the controversy was pure serendipity. A more difficult model of 4 parameters would have been hard to find." The long running public conflict of Fisher with Karl Pearson can be followed in a number of articles in prestigious journals. For example, concerning the estimation of the four parameters for the beta distribution, and Fisher's criticism of Pearson's method of moments as being arbitrary, see Pearson's article "Method of moments and method of maximum likelihood" [44] (published three years after his retirement from University College, London, where his position had been divided between Fisher and Pearson's son Egon) in which Pearson writes "I read (Koshai's paper in the Journal of the Royal Statistical Society, 1933) which as far as I am aware is the only case at present published of the application of Professor Fisher's method. To my astonishment that method depends on first working out the constants of the frequency curve by the (Pearson) Method of Moments and then superposing on it, by what Fisher terms "the Method of Maximum Likelihood" a further approximation to obtain, what he holds, he will thus get, 'more efficient values' of the curve constants".
David and Edwards's treatise on the history of statistics[80] cites the first modern treatment of the beta distribution, in 1911,[81] using the beta designation that has become standard, due to Corrado Gini, an Italian statistician, demographer, and sociologist, who developed the Gini coefficient. N.L.Johnson and S.Kotz, in their comprehensive and very informative monograph[82] on leading historical personalities in statistical sciences credit Corrado Gini[83] as "an early Bayesian...who dealt with the problem of eliciting the parameters of an initial Beta distribution, by singling out techniques which anticipated the advent of the so-called empirical Bayes approach."
References
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). "Chapter 25: Beta Distributions". Continuous Univariate Distributions Vol. 2 (2nd ed.). Wiley. ISBN 978-0-471-58494-0.
- ^ a b Rose, Colin; Smith, Murray D. (2002). Mathematical Statistics with MATHEMATICA. Springer. ISBN 978-0387952345.
- ^ a b c Kruschke, John K. (2011). Doing Bayesian data analysis: A tutorial with R and BUGS. Academic Press / Elsevier. p. 83. ISBN 978-0123814852.
- ^ a b Berger, James O. (2010). Statistical Decision Theory and Bayesian Analysis (2nd ed.). Springer. ISBN 978-1441930743.
- ^ a b c d Feller, William (1971). An Introduction to Probability Theory and Its Applications, Vol. 2. Wiley. ISBN 978-0471257097.
- ^ Kruschke, John K. (2015). Doing Bayesian Data Analysis: A Tutorial with R, JAGS and Stan. Academic Press / Elsevier. ISBN 978-0-12-405888-0.
- ^ a b Wadsworth, George P. and Joseph Bryan (1960). Introduction to Probability and Random Variables. McGraw-Hill.
- ^ a b c d e f g Gupta, Arjun K., ed. (2004). Handbook of Beta Distribution and Its Applications. CRC Press. ISBN 978-0824753962.
- ^ a b Kerman, Jouni (2011). "A closed-form approximation for the median of the beta distribution". arXiv:1111.0433 [math.ST].
- ^ Mosteller, Frederick and John Tukey (1977). Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley Pub. Co. Bibcode:1977dars.book.....M. ISBN 978-0201048544.
- ^ a b Feller, William (1968). An Introduction to Probability Theory and Its Applications. Vol. 1 (3rd ed.). ISBN 978-0471257080.
- ^ Philip J. Fleming and John J. Wallace. How not to lie with statistics: the correct way to summarize benchmark results. Communications of the ACM, 29(3):218–221, March 1986.
- ^ "NIST/SEMATECH e-Handbook of Statistical Methods 1.3.6.6.17. Beta Distribution". National Institute of Standards and Technology Information Technology Laboratory. April 2012. Retrieved May 31, 2016.
- ^ Oguamanam, D.C.D.; Martin, H. R.; Huissoon, J. P. (1995). "On the application of the beta distribution to gear damage analysis". Applied Acoustics. 45 (3): 247–261. doi:10.1016/0003-682X(95)00001-P.
- ^ Zhiqiang Liang; Jianming Wei; Junyu Zhao; Haitao Liu; Baoqing Li; Jie Shen; Chunlei Zheng (27 August 2008). "The Statistical Meaning of Kurtosis and Its New Application to Identification of Persons Based on Seismic Signals". Sensors. 8 (8): 5106–5119. Bibcode:2008Senso...8.5106L. doi:10.3390/s8085106. PMC 3705491. PMID 27873804.
- ^ Kenney, J. F., and E. S. Keeping (1951). Mathematics of Statistics Part Two, 2nd edition. D. Van Nostrand Company Inc.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ a b c d Abramowitz, Milton and Irene A. Stegun (1965). Handbook Of Mathematical Functions With Formulas, Graphs, And Mathematical Tables. Dover. ISBN 978-0-486-61272-0.
- ^ Weisstein., Eric W. "Kurtosis". MathWorld--A Wolfram Web Resource. Retrieved 13 August 2012.
- ^ a b Panik, Michael J (2005). Advanced Statistics from an Elementary Point of View. Academic Press. ISBN 978-0120884940.
- ^ a b c d e f Pearson, Karl (1916). "Mathematical contributions to the theory of evolution, XIX: Second supplement to a memoir on skew variation". Philosophical Transactions of the Royal Society A. 216 (538–548): 429–457. Bibcode:1916RSPTA.216..429P. doi:10.1098/rsta.1916.0009. JSTOR 91092.
- ^ Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan (2015) [October 2014]. Zwillinger, Daniel; Moll, Victor Hugo (eds.). Table of Integrals, Series, and Products. Translated by Scripta Technica, Inc. (8 ed.). Academic Press, Inc. ISBN 978-0-12-384933-5. LCCN 2014010276.
- ^ Billingsley, Patrick (1995). "30". Probability and measure (3rd ed.). Wiley-Interscience. ISBN 978-0-471-00710-4.
- ^ a b MacKay, David (2003). Information Theory, Inference and Learning Algorithms. Cambridge University Press; First Edition. Bibcode:2003itil.book.....M. ISBN 978-0521642989.
- ^ a b Johnson, N.L. (1949). "Systems of frequency curves generated by methods of translation" (PDF). Biometrika. 36 (1–2): 149–176. doi:10.1093/biomet/36.1-2.149. hdl:10338.dmlcz/135506. PMID 18132090.
- ^ Verdugo Lazo, A. C. G.; Rathie, P. N. (1978). "On the entropy of continuous probability distributions". IEEE Trans. Inf. Theory. 24 (1): 120–122. doi:10.1109/TIT.1978.1055832.
- ^ Shannon, Claude E. (1948). "A Mathematical Theory of Communication". Bell System Technical Journal. 27 (4): 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x.
- ^ a b c Cover, Thomas M. and Joy A. Thomas (2006). Elements of Information Theory 2nd Edition (Wiley Series in Telecommunications and Signal Processing). Wiley-Interscience; 2 edition. ISBN 978-0471241959.
- ^ Plunkett, Kim, and Jeffrey Elman (1997). Exercises in Rethinking Innateness: A Handbook for Connectionist Simulations (Neural Network Modeling and Connectionism). A Bradford Book. p. 166. ISBN 978-0262661058.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Nallapati, Ramesh (2006). The smoothed dirichlet distribution: understanding cross-entropy ranking in information retrieval (Thesis). Computer Science Dept., University of Massachusetts Amherst.
- ^ a b Pearson, Egon S. (July 1969). "Some historical reflections traced through the development of the use of frequency curves". THEMIS Statistical Analysis Research Program, Technical Report 38. Office of Naval Research, Contract N000014-68-A-0515 (Project NR 042–260).
- ^ Hahn, Gerald J.; Shapiro, S. (1994). Statistical Models in Engineering (Wiley Classics Library). Wiley-Interscience. ISBN 978-0471040651.
- ^ a b Pearson, Karl (1895). "Contributions to the mathematical theory of evolution, II: Skew variation in homogeneous material". Philosophical Transactions of the Royal Society. 186: 343–414. Bibcode:1895RSPTA.186..343P. doi:10.1098/rsta.1895.0010. JSTOR 90649.
- ^ Buchanan, K.; Rockway, J.; Sternberg, O.; Mai, N. N. (May 2016). "Sum-difference beamforming for radar applications using circularly tapered random arrays". 2016 IEEE Radar Conference (RadarConf). pp. 1–5. doi:10.1109/RADAR.2016.7485289. ISBN 978-1-5090-0863-6. S2CID 32525626.
- ^ Buchanan, K.; Flores, C.; Wheeland, S.; Jensen, J.; Grayson, D.; Huff, G. (May 2017). "Transmit beamforming for radar applications using circularly tapered random arrays". 2017 IEEE Radar Conference (RadarConf). pp. 0112–0117. doi:10.1109/RADAR.2017.7944181. ISBN 978-1-4673-8823-8. S2CID 38429370.
- ^ Ryan, Buchanan, Kristopher (2014-05-29). "Theory and Applications of Aperiodic (Random) Phased Arrays".
{{cite journal}}: Cite journal requires|journal=(help)CS1 maint: multiple names: authors list (link) - ^ Herrerías-Velasco, José Manuel and Herrerías-Pleguezuelo, Rafael and René van Dorp, Johan. (2011). Revisiting the PERT mean and Variance. European Journal of Operational Research (210), p. 448–451.
- ^ a b Malcolm, D. G.; Roseboom, J. H.; Clark, C. E.; Fazar, W. (September–October 1958). "Application of a Technique for Research and Development Program Evaluation". Operations Research. 7 (5): 646–669. doi:10.1287/opre.7.5.646. ISSN 0030-364X.
- ^ a b c d David, H. A., Nagaraja, H. N. (2003) Order Statistics (3rd Edition). Wiley, New Jersey pp 458. ISBN 0-471-38926-9
- ^ "Beta distribution". www.statlect.com.
- ^ "1.3.6.6.17. Beta Distribution". www.itl.nist.gov.
- ^ a b c d e f g h Elderton, William Palin (1906). Frequency-Curves and Correlation. Charles and Edwin Layton (London).
- ^ Elderton, William Palin and Norman Lloyd Johnson (2009). Systems of Frequency Curves. Cambridge University Press. ISBN 978-0521093361.
- ^ a b c Bowman, K. O.; Shenton, L. R. (2007). "The beta distribution, moment method, Karl Pearson and R.A. Fisher" (PDF). Far East J. Theo. Stat. 23 (2): 133–164.
- ^ a b Pearson, Karl (June 1936). "Method of moments and method of maximum likelihood". Biometrika. 28 (1/2): 34–59. doi:10.2307/2334123. JSTOR 2334123.
- ^ a b c Joanes, D. N.; C. A. Gill (1998). "Comparing measures of sample skewness and kurtosis". The Statistician. 47 (Part 1): 183–189. doi:10.1111/1467-9884.00122.
- ^ Beckman, R. J.; G. L. Tietjen (1978). "Maximum likelihood estimation for the beta distribution". Journal of Statistical Computation and Simulation. 7 (3–4): 253–258. doi:10.1080/00949657808810232.
- ^ Gnanadesikan, R., Pinkham and Hughes (1967). "Maximum likelihood estimation of the parameters of the beta distribution from smallest order statistics". Technometrics. 9 (4): 607–620. doi:10.2307/1266199. JSTOR 1266199.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Fackler, Paul. "Inverse Digamma Function (Matlab)". Harvard University School of Engineering and Applied Sciences. Retrieved 2012-08-18.
- ^ a b c Silvey, S.D. (1975). Statistical Inference. Chapman and Hal. p. 40. ISBN 978-0412138201.
- ^ Edwards, A. W. F. (1992). Likelihood. The Johns Hopkins University Press. ISBN 978-0801844430.
- ^ a b c d e f Jaynes, E.T. (2003). Probability theory, the logic of science. Cambridge University Press. ISBN 978-0521592710.
- ^ Costa, Max, and Cover, Thomas (September 1983). On the similarity of the entropy power inequality and the Brunn Minkowski inequality (PDF). Tech.Report 48, Dept. Statistics, Stanford University.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ a b c Aryal, Gokarna; Saralees Nadarajah (2004). "Information matrix for beta distributions" (PDF). Serdica Mathematical Journal (Bulgarian Academy of Science). 30: 513–526.
- ^ a b Laplace, Pierre Simon, marquis de (1902). A philosophical essay on probabilities. New York : J. Wiley; London : Chapman & Hall. ISBN 978-1-60206-328-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Cox, Richard T. (1961). Algebra of Probable Inference. The Johns Hopkins University Press. ISBN 978-0801869822.
- ^ a b Keynes, John Maynard (2010) [1921]. A Treatise on Probability: The Connection Between Philosophy and the History of Science. Wildside Press. ISBN 978-1434406965.
- ^ Pearson, Karl (1907). "On the Influence of Past Experience on Future Expectation". Philosophical Magazine. 6 (13): 365–378.
- ^ a b c d Jeffreys, Harold (1998). Theory of Probability. Oxford University Press, 3rd edition. ISBN 978-0198503682.
- ^ Broad, C. D. (October 1918). "On the relation between induction and probability". MIND, A Quarterly Review of Psychology and Philosophy. 27 (New Series) (108): 389–404. doi:10.1093/mind/XXVII.4.389. JSTOR 2249035.
- ^ a b c d Perks, Wilfred (January 1947). "Some observations on inverse probability including a new indifference rule". Journal of the Institute of Actuaries. 73 (2): 285–334. doi:10.1017/S0020268100012270. Archived from the original on 2014-01-12. Retrieved 2012-09-19.
- ^ a b Bayes, Thomas; communicated by Richard Price (1763). "An Essay towards solving a Problem in the Doctrine of Chances". Philosophical Transactions of the Royal Society. 53: 370–418. doi:10.1098/rstl.1763.0053. JSTOR 105741.
- ^ Haldane, J.B.S. (1932). "A note on inverse probability". Mathematical Proceedings of the Cambridge Philosophical Society. 28 (1): 55–61. Bibcode:1932PCPS...28...55H. doi:10.1017/s0305004100010495. S2CID 122773707.
- ^ Zellner, Arnold (1971). An Introduction to Bayesian Inference in Econometrics. Wiley-Interscience. ISBN 978-0471169376.
- ^ Jeffreys, Harold (September 1946). "An Invariant Form for the Prior Probability in Estimation Problems". Proceedings of the Royal Society. A 24. 186 (1007): 453–461. Bibcode:1946RSPSA.186..453J. doi:10.1098/rspa.1946.0056. PMID 20998741.
- ^ Berger, James; Bernardo, Jose; Sun, Dongchu (2009). "The formal definition of reference priors". The Annals of Statistics. 37 (2): 905–938. arXiv:0904.0156. Bibcode:2009arXiv0904.0156B. doi:10.1214/07-AOS587. S2CID 3221355.
- ^ Clarke, Bertrand S.; Andrew R. Barron (1994). "Jeffreys' prior is asymptotically least favorable under entropy risk" (PDF). Journal of Statistical Planning and Inference. 41: 37–60. doi:10.1016/0378-3758(94)90153-8.
- ^ Pearson, Karl (1892). The Grammar of Science. Walter Scott, London.
- ^ Pearson, Karl (2009). The Grammar of Science. BiblioLife. ISBN 978-1110356119.
- ^ Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B. (2003). Bayesian Data Analysis. Chapman and Hall/CRC. ISBN 978-1584883883.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ A. Jøsang. A Logic for Uncertain Probabilities. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. 9(3), pp.279-311, June 2001. PDF[permanent dead link]
- ^ H.M. de Oliveira and G.A.A. Araújo,. Compactly Supported One-cyclic Wavelets Derived from Beta Distributions. Journal of Communication and Information Systems. vol.20, n.3, pp.27-33, 2005.
- ^ Balding, David J.; Nichols, Richard A. (1995). "A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity". Genetica. 96 (1–2). Springer: 3–12. doi:10.1007/BF01441146. PMID 7607457. S2CID 30680826.
- ^ Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1086–1091.
- ^ Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595–609.
- ^ "Defense Resource Management Institute - Naval Postgraduate School". www.nps.edu.
- ^ van der Waerden, B. L., "Mathematical Statistics", Springer, ISBN 978-3-540-04507-6.
- ^ On normalizing the incomplete beta-function for fitting to dose-response curves M.E. Wise Biometrika vol 47, No. 1/2, June 1960, pp. 173–175
- ^ Yule, G. U.; Filon, L. N. G. (1936). "Karl Pearson. 1857–1936". Obituary Notices of Fellows of the Royal Society. 2 (5): 72. doi:10.1098/rsbm.1936.0007. JSTOR 769130.
- ^ "Library and Archive catalogue". Sackler Digital Archive. Royal Society. Archived from the original on 2011-10-25. Retrieved 2011-07-01.
- ^ David, H. A. and A.W.F. Edwards (2001). Annotated Readings in the History of Statistics. Springer; 1 edition. ISBN 978-0387988443.
- ^ Gini, Corrado (1911). "Considerazioni Sulle Probabilità Posteriori e Applicazioni al Rapporto dei Sessi Nelle Nascite Umane". Studi Economico-Giuridici della Università de Cagliari. Anno III (reproduced in Metron 15, 133, 171, 1949): 5–41.
- ^ Johnson, Norman L. and Samuel Kotz, ed. (1997). Leading Personalities in Statistical Sciences: From the Seventeenth Century to the Present (Wiley Series in Probability and Statistics. Wiley. ISBN 978-0471163817.
- ^ Metron journal. "Biography of Corrado Gini". Metron Journal. Archived from the original on 2012-07-16. Retrieved 2012-08-18.
External links
- "Beta Distribution" by Fiona Maclachlan, the Wolfram Demonstrations Project, 2007.
- Beta Distribution – Overview and Example, xycoon.com
- Beta Distribution, brighton-webs.co.uk
- Beta Distribution Video, exstrom.com
- "Beta-distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Beta Distribution". MathWorld.
- Harvard University Statistics 110 Lecture 23 Beta Distribution, Prof. Joe Blitzstein
![{\displaystyle x\en [0,1]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09601f74a28f3e2cad381be1a915ab0c02fe39c6)





![{\displaystyle \operatorname {E} [X]={\frac {\alpha }{\alpha +\beta }}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3905662ceed484cba5580951e29eda96f4d2605e)
![{\displaystyle \operatorname {E} [\ln X]=\psi (\alpha )-\psi (\alpha +\beta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de67df996fa33237ab7f415e7edc9fa8e71997a0)
![{\displaystyle \operatorname {E} [X\,\ln X]={\frac {\alpha }{\alpha +\beta }}\,\left[\psi (\alpha +1)-\psi (\alpha +\beta +1)\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50106a787db7d72ce3066a5a3238813cffebcc2e)

![{\displaystyle {\begin{matrix}I_{\frac {1}{2}}^{[-1]}(\alpha ,\beta ){\text{ (en general) }}\\[0.5em]\approx {\frac {\alpha -{\tfrac {1}{3}}}{\alpha +\beta -{\tfrac {2}{3}}}}{\text{ para }}\alpha ,\beta >1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af887ef0331cde970dad14ad670cf3592334f845)


![{\displaystyle \operatorname {var} [X]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90a6ad61b4b436749ca37a6c2a1aa077b032ce3)
![{\displaystyle \operatorname {var} [\ln X]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4941f45412823abd34d3befea7f8fbf544135e4)

![{\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea65a8d7c9e00ba6299b727eab679117776f41e)
![{\displaystyle {\begin{matriz}\ln \mathrm {B} (\alfa ,\beta )-(\alfa -1)\psi (\alfa )-(\beta -1)\psi (\beta )\\[0.5em]{}+(\alfa +\beta -2)\psi (\alfa +\beta )\end{matriz}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff4b6cc1848fe96318adb734393b701cb816f88a)


![{\displaystyle {\begin{bmatrix}\operatorname {var} [\ln X]&\operatorname {cov} [\ln X,\ln(1-X)]\\\operatorname {cov} [\ln X, \ln(1-X)]&\operatorname {var} [\ln(1-X)]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/881f91af0ab1d6bf3809a4ed6ca9e6384544292f)
}{V[X]}}-1\right)E[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b596a180ef813a0baa1d6f2063950e20da1f62)
}{V[X]}}-1\right)(1-E[X])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ace15e23f6ac9be43eea861f44c018fd3d00de)






![{\displaystyle {\begin{aligned}f(x;\alpha ,\beta )&=\mathrm {constante} \cdot x^{\alpha -1}(1-x)^{\beta -1}\\ [3pt]&={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\displaystyle \int _{0}^{1}u^{\alpha -1 }(1-u)^{\beta -1}\,du}}\\[6pt]&={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\ beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\\[6pt]&={\frac {1}{\mathrm {B} (\alpha ,\ beta )}}x^{\alpha -1}(1-x)^{\beta -1}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc18388353b219c482e8e35ca4aae808ab1be81)







































![{\displaystyle {\begin{aligned}\mu _{Y}&=\mu _{X}(ca)+a\\&=\left({\frac {\alpha }{\alpha +\beta }}\right)(ca)+a={\frac {\alpha c+\beta a}{\alpha +\beta }}\\[8pt]{\text{moda}}(Y)&={\text{moda}}(X)(ca)+a\\&=\left({\frac {\alpha -1}{\alpha +\beta -2}}\right)(ca)+a={\frac {(\alpha -1)c+(\beta -1)a}{\alpha +\beta -2}}\ ,\qquad {\text{si }}\alpha ,\beta >1\\[8pt]{\text{mediana}}(Y)&={\text{mediana}}(X)(ca)+a\\&=\left(I_{\frac {1}{2}}^{[-1]}(\alpha ,\beta )\right)(ca)+a\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f65af6c528ca47e8838d3d5722a94f9e3f128100)





![{\displaystyle {\text{exceso de curtosis}}(Y)={\text{exceso de curtosis}}(X)={\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99ddb3577b02ee0b10163123af23c6d7f728946b)

![{\displaystyle x=I_{1/2}^{[-1]}(\alpha ,\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7510f94efa49f254eb3924678b527a6fd22d0fc)





![Abs[(Mediana-Aprox.)/Mediana] para la distribución beta para 1 ≤ α ≤ 5 y 1 ≤ β ≤ 5](http://upload.wikimedia.org/wikipedia/commons/thumb/a/af/Relative_Error_for_Approximation_to_Median_of_Beta_Distribution_for_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg/440px-Relative_Error_for_Approximation_to_Median_of_Beta_Distribution_for_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg)
![Abs[(Mediana-Aprox.)/(Media-Moda)] para la distribución beta para 1≤α≤5 y 1≤β≤5](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e8/Error_in_Median_Apprx._relative_to_Mean-Mode_distance_for_Beta_Distribution_with_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg/440px-Error_in_Median_Apprx._relative_to_Mean-Mode_distance_for_Beta_Distribution_with_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg)
![{\displaystyle {\begin{aligned}\mu =\operatorname {E} [X]&=\int _{0}^{1}xf(x;\alpha ,\beta )\,dx\\&=\int _{0}^{1}x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\,dx\\&={\frac {\alpha }{\alpha +\beta }}\\&={\frac {1}{1+{\frac {\beta }{\alpha }}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9137834d9d47360ed6c23550c6236fed5fd35f7)


![{\displaystyle \ln G_{X}=\nombre del operador {E} [\ln X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64b67cb73b90bc0e09ba41003b44f84b6e1d3feb)
![{\displaystyle {\begin{aligned}\operatorname {E} [\ln X]&=\int _{0}^{1}\ln x\,f(x;\alpha ,\beta )\,dx\\[4pt]&=\int _{0}^{1}\ln x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\,dx\\[4pt]&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\,\int _{0}^{1}{\frac {\partial x^{\alpha -1}(1-x)^{\beta -1}}{\partial \alpha }}\,dx\\[4pt]&={\frac {1}{\mathrm {B} (\alfa ,\beta )}}{\frac {\parcial }{\parcial \alfa }}\int _{0}^{1}x^{\alfa -1}(1-x)^{\beta -1}\,dx\\[4pt]&={\frac {1}{\mathrm {B} (\alfa ,\beta )}}{\frac {\parcial \mathrm {B} (\alfa ,\beta )}{\parcial \alfa }}\\[4pt]&={\frac {\parcial \ln \mathrm {B} (\alfa ,\beta )}{\parcial \alfa }}\\[4pt]&={\frac {\parcial \ln \Gamma (\alfa )}{\parcial \alfa }}-{\frac {\parcial \ln \Gamma (\alfa +\beta )}{\parcial \alpha }}\\[4pt]&=\psi (\alpha )-\psi (\alpha +\beta )\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd9db519e08e3c72cd6f9e2f0c90a7c57bdba035)
![{\displaystyle G_{X}=e^{\operatorname {E} [\ln X]}=e^{\psi (\alpha )-\psi (\alpha +\beta )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c93ffa7f0155fa3816fcb151c3eb677700aabca2)




![{\displaystyle G_{(1-X)}=e^{\operatorname {E} [\ln(1-X)]}=e^{\psi (\beta )-\psi (\alpha +\beta ) }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8013e6a62bd5140a4e7919686761225dd54847e)




![{\displaystyle {\begin{aligned}H_{X}&={\frac {1}{\operatorname {E} \left[{\frac {1}{X}}\right]}}\\&={\frac {1}{\int _{0}^{1}{\frac {f(x;\alpha ,\beta )}{x}}\,dx}}\\&={\frac {1}{\int _{0}^{1}{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{x\mathrm {B} (\alpha ,\beta )}}\,dx}}\\&={\frac {\alpha -1}{\alpha +\beta -1}}{\text{ si }}\alpha >1{\text{ y }}\beta >0\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed7d99dd7493b9c085cd5d407861730e2a2abf6c)


![{\displaystyle H_{1-X}={\frac {1}{\operatorname {E} \left[{\frac {1}{1-X}}\right]}}={\frac {\beta -1}{\alpha +\beta -1}}{\text{ si }}\beta >1,{\text{ y }}\alpha >0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48f4fd69f20c4259cb8a50e754df8dfed5a1ddca)



![{\displaystyle \operatorname {var} (X)=\operatorname {E} [(X-\mu )^{2}]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96555f71897dc80e2f31ec71b3cbfbcf39950bc)






![{\displaystyle {\begin{aligned}\ln \operatorname {var} _{GX}&=\operatorname {E} \left[(\ln X-\ln G_{X})^{2}\right]\\&=\operatorname {E} [(\ln X-\operatorname {E} \left[\ln X])^{2}\right]\\&=\operatorname {E} \left[(\ln X)^{2}\right]-(\operatorname {E} [\ln X])^{2}\\&=\operatorname {var} [\ln X]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5737429860855b238c6ac72ae064e4bb6d8cb772)
![{\displaystyle \operatorname {var} _{GX}=e^{\operatorname {var} [\ln X]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/524cf664ccfd5eb381fd1987926209f1c401a200)
![{\displaystyle {\begin{aligned}\ln \nombreoperador {var_{G(1-X)}} &=\nombreoperador {E} [(\ln(1-X)-\ln G_{1-X})^{2}]\\&=\nombreoperador {E} [(\ln(1-X)-\nombreoperador {E} [\ln(1-X)])^{2}]\\&=\nombreoperador {E} [(\ln(1-X))^{2}]-(\nombreoperador {E} [\ln(1-X)])^{2}\\&=\nombreoperador {var} [\ln(1-X)]\\&\\\nombreoperador {var_{G(1-X)}} &=e^{\nombreoperador {var} [\ln(1-X)]}\\&\\\ln \nombreoperador {cov_{G{X,1-X}}} &=\operatorname {E} [(\ln X-\ln G_{X})(\ln(1-X)-\ln G_{1-X})]\\&=\operatorname {E} [(\ln X-\operatorname {E} [\ln X])(\ln(1-X)-\operatorname {E} [\ln(1-X)])]\\&=\ nombre del operador {E} \left[\ln X\ln(1-X)\right]-\nombre del operador {E} [\ln X]\nombre del operador {E} [\ln(1-X)]\\&=\nombre del operador {cov} [\ln X,\ln(1-X)]\\&\\\nombre del operador {cov} _{G{X,(1-X)}}&=e^{\nombre del operador {cov} [\ln X,\ln(1-X)]}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9951a17fba87115b493918bfd9271c8e2193d0a8)
![{\displaystyle \operatorname {var} [\ln X]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e396e8700267735eb741f73e8906445579c43bc6)
![{\displaystyle \operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70eefadef46c7d56cc13c8221aa3df1d71596b7f)
![{\displaystyle \operatorname {cov} [\ln X,\ln(1-X)]=-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7a515ada0b9d62c5a3a7b35662b03256d66e3b9)

![{\displaystyle \ln \operatorname {var} _{GX}=\operatorname {var} [\ln X]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/194b00552edda5d8d026a24872cdb27b604516c9)
![{\displaystyle \ln \operatorname {var} _{G(1-X)}=\operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96dd82553307c025c84da68a3c373aad7467abd2)
![{\displaystyle \ln \operatorname {cov} _{GX,1-X}=\operatorname {cov} [\ln X,\ln(1-X)]=-\psi _{1}(\alpha +\ beta)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a793c0271e457f671edb0668edc15bbae8740f)




![{\displaystyle \operatorname {E} [|XE[X]|]={\frac {2\alpha ^{\alpha }\beta ^{\beta }}{\mathrm {B} (\alpha ,\beta ) (\alpha +\beta )^{\alpha +\beta +1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d1c6330a91df22b40cedc7903dbc70120d66cf9)
![{\displaystyle {\begin{aligned}{\frac {\text{desviación media absoluta de la media}}{\text{desviación estándar}}}&={\frac {\operatorname {E} [|XE[X]|]}{\sqrt {\operatorname {var} (X)}}}\\&\approx {\sqrt {\frac {2}{\pi }}}\left(1+{\frac {7}{12(\alpha +\beta )}}{}-{\frac {1}{12\alpha }}-{\frac {1}{12\beta }}\right),{\text{si }}\alpha ,\beta >1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c196a5a2eb110b71471a3dc019241c6cb8c3f927)


![{\displaystyle \operatorname {E} [|XE[X]|]={\frac {2\mu ^{\mu \nu }(1-\mu )^{(1-\mu )\nu }}{ \nu \mathrm {B} (\mu \nu ,(1-\mu )\nu )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027efecf8aaefea8c805194e47a1374ffcb63cb8)
![{\displaystyle {\begin{aligned}\operatorname {E} [|XE[X]|]={\frac {2^{1-\nu }}{\nu \mathrm {B} ({\tfrac {\ nu }{2}},{\tfrac {\nu }{2}})}}&={\frac {2^{1-\nu }\Gamma (\nu )}{\nu (\Gamma ({ \tfrac {\nu }{2}}))^{2}}}\\\lim _{\nu \to 0}\left(\lim _{\mu \to {\frac {1}{2} }}\operatorname {E} [|XE[X]|]\right)&={\tfrac {1}{2}}\\\lim _{\nu \to \infty }\left(\lim _{ \mu \to {\frac {1}{2}}}\operatorname {E} [|XE[X]|]\right)&=0\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87aa0eff7a4da0f5abe2d211e2b7dda8c8fff801)
![{\displaystyle {\begin{aligned}\lim _{\beta \to 0}\operatorname {E} [|XE[X]|]&=\lim _{\alpha \to 0}\operatorname {E} [ |XE[X]|]=0\\\lim _{\beta \to \infty }\operatorname {E} [|XE[X]|]&=\lim _{\alpha \to \infty }\operatorname {E} [|XE[X]|]=0\\\lim _{\mu \to 0}\operatorname {E} [|XE[X]|]&=\lim _{\mu \to 1} \operatorname {E} [|XE[X]|]=0\\\lim _{\nu \to 0}\operatorname {E} [|XE[X]|]&={\sqrt {\mu (1-\mu )}}\\\lim _{\nu \to \infty }\operatorname {E} [|XE[X]|]&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87c43b4a05f8ea3acf3f15b0a16f6ee07811ac6b)


![{\displaystyle \gamma _{1}={\frac {\operatorname {E} [(X-\mu )^{3}]}{(\operatorname {var} (X))^{3/2}}}={\frac {2(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2334c6fa1e6326760870b716521460bba115a92)

![{\displaystyle \gamma _{1}={\frac {\operatorname {E} [(X-\mu )^{3}]}{(\operatorname {var} (X))^{3/2}} }={\frac {2(1-2\mu ){\sqrt {1+\nu }}}{(2+\nu ){\sqrt {\mu (1-\mu )}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d71042628a42bfedc972e01f8ba5c27f63c3fae4)
![{\displaystyle \gamma _{1}={\frac {\operatorname {E} [(X-\mu )^{3}]}{(\operatorname {var} (X))^{3/2}}}={\frac {2(1-2\mu ){\sqrt {\text{ var }}}}{\mu (1-\mu )+\operatorname {var} }}{\text{ if }}\operatorname {var} <\mu (1-\mu )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e30c818c1af07028336494d35562333ffd903f1)
![{\displaystyle (\gamma _{1})^{2}={\frac {(\operatorname {E} [(X-\mu )^{3}])^{2}}{(\operatorname {var} (X))^{3}}}={\frac {4}{(2+\nu )^{2}}}{\bigg (}{\frac {1}{\text{var}}}-4(1+\nu ){\bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d9343b5e45ab6ac483a8f0fb8efd1699e0158d)





![{\displaystyle {\begin{aligned}{\text{exceso de curtosis}}&={\text{curtosis}}-3\\&={\frac {\operatorname {E} [(X-\mu )^{4}]}{(\operatorname {var} (X))^{2}}}-3\\&={\frac {6[\alpha ^{3}-\alpha ^{2}(2\beta -1)+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}\\&={\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed8320d4f38ba9260f8ad91c30238abc08306dc8)











![{\displaystyle {\begin{aligned}\varphi _{X}(\alpha ;\beta ;t)&=\operatorname {E} \left[e^{itX}\right]\\&=\int _{0}^{1}e^{itx}f(x;\alpha ,\beta )\,dx\\&={}_{1}F_{1}(\alpha ;\alpha +\beta ;it)\!\\&=\sum _{n=0}^{\infty }{\frac {\alpha ^{(n)}(it)^{n}}{(\alpha +\beta )^{(n)}n!}}\\&=1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {(it)^{k}}{k!}}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dac7a59df675d0b8758523c87e85888609a213c)


![{\displaystyle \operatorname {Re} \left[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)\right]=\operatorname {Re} \left[{}_{1}F_{1}(\alpha ;\alpha +\beta ;-it)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/468f2135d76bd1b522c84092679209ff6abd5845)
![{\displaystyle \operatorname {Im} \left[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)\right]=-\operatorname {Im} \left[{}_{1}F_{1}(\alpha ;\alpha +\beta ;-it)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fca8984292cc85cb8a37ecb5a2b7c04b5596282)


![{\displaystyle {\begin{aligned}M_{X}(\alpha ;\beta ;t)&=\operatorname {E} \left[e^{tX}\right]\\[4pt]&=\int _{0}^{1}e^{tx}f(x;\alpha ,\beta )\,dx\\[4pt]&={}_{1}F_{1}(\alpha ;\alpha +\beta ;t)\\[4pt]&=\sum _{n=0}^{\infty }{\frac {\alpha ^{(n)}}{(\alpha +\beta )^{(n)}}}{\frac {t^{n}}{n!}}\\[4pt]&=1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\derecha){\frac {t^{k}}{k!}}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e664dd90aeae487c19dc89c87c7d1abe47bfcf3d)


![{\displaystyle \operatorname {E} [X^{k}]={\frac {\alpha ^{(k)}}{(\alpha +\beta )^{(k)}}}=\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e03c03f31b903a1bc73ea8b637e3134b110a85a2)
![{\displaystyle \operatorname {E} [X^{k}]={\frac {\alpha +k-1}{\alpha +\beta +k-1}}\operatorname {E} [X^{k-1}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/069cb373a905b1e8a5a82a0e3b028e88f63672e2)

![{\displaystyle {\begin{aligned}\operatorname {E} [1-X]&={\frac {\beta }{\alpha +\beta }}\\\operatorname {E} [X(1-X)]&=\operatorname {E} [(1-X)X]={\frac {\alpha \beta }{(\alpha +\beta )(\alpha +\beta +1)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fc49b9eafccd56d39c236b26d222dde51638ce)
![{\displaystyle \operatorname {var} [(1-X)]=\operatorname {var} [X]=-\operatorname {cov} [X,(1-X)]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7273cc84a6c789724b985c34059fa75a62bce631)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[{\frac {1}{X}}\right]&={\frac {\alpha +\beta -1}{\alpha -1}}&&{\text{ si }}\alpha >1\\\operatorname {E} \left[{\frac {1}{1-X}}\right]&={\frac {\alpha +\beta -1}{\beta -1}}&&{\text{ si }}\beta >1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972a9c1853e6991aac6666b06c0a633a0caad5b7)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[{\frac {X}{1-X}}\right]&={\frac {\alpha }{\beta -1}}&&{\text{ si }}\beta >1\\\operatorname {E} \left[{\frac {1-X}{X}}\right]&={\frac {\beta }{\alpha -1}}&&{\text{ si }}\alpha >1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db2a0928a7f906bcbe5cfd9d0c57713c9ab5cfb7)
![{\displaystyle \operatorname {var} \left[{\frac {1}{X}}\right]=\operatorname {E} \left[\left({\frac {1}{X}}-\operatorname {E} \left[{\frac {1}{X}}\right]\right)^{2}\right]=\operatorname {var} \left[{\frac {1-X}{X}}\right]=\operatorname {E} \left[\left({\frac {1-X}{X}}-\operatorname {E} \left[{\frac {1-X}{X}}\right]\right)^{2}\right]={\frac {\beta (\alpha +\beta -1)}{(\alpha -2)(\alpha -1)^{2}}}{\text{ if }}\alpha >2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af7a7cb782c6c42658374ac45365cde388c2326a)
![{\displaystyle \operatorname {var} \left[{\frac {1}{1-X}}\right]=\operatorname {E} \left[\left({\frac {1}{1-X}}-\operatorname {E} \left[{\frac {1}{1-X}}\right]\right)^{2}\right]=\operatorname {var} \left[{\frac {X}{1-X}}\right]=\operatorname {E} \left[\left({\frac {X}{1-X}}-\operatorname {E} \left[{\frac {X}{1-X}}\right]\right)^{2}\right]={\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}{\text{ if }}\beta >2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22dd8c7aad68227962947ad69019b01a79c41b6d)
![{\displaystyle \operatorname {cov} \left[{\frac {1}{X}},{\frac {1}{1-X}}\right]=\operatorname {cov} \left[{\frac {1-X}{X}},{\frac {X}{1-X}}\right]=\operatorname {cov} \left[{\frac {1}{X}},{\frac {X}{1-X}}\right]=\operatorname {cov} \left[{\frac {1-X}{X}},{\frac {1}{1-X}}\right]={\frac {\alpha +\beta -1}{(\alpha -1)(\beta -1)}}{\text{ si }}\alpha ,\beta >1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa2342c3fe24a7ed5b840fd9583c055aa5791486)
![{\displaystyle {\begin{aligned}\operatorname {E} [\ln(X)]&=\psi (\alpha )-\psi (\alpha +\beta )=-\operatorname {E} \left[\ln \left({\frac {1}{X}}\right)\right],\\\operatorname {E} [\ln(1-X)]&=\psi (\beta )-\psi (\alpha +\beta )=-\operatorname {E} \left[\ln \left({\frac {1}{1-X}}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6125bcdc7551c82f7451b444b941c97b83abdf20)

![{\displaystyle {\begin{aligned}\operatorname {E} \left[\ln \left({\frac {X}{1-X}}\right)\right]&=\psi (\alpha )-\psi (\beta )=\operatorname {E} [\ln(X)]+\operatorname {E} \left[\ln \left({\frac {1}{1-X}}\right)\right],\\\operatorname {E} \left[\ln \left({\frac {1-X}{X}}\right)\right]&=\psi (\beta )-\psi (\alpha )=-\operatorname {E} \left[\ln \left({\frac {X}{1-X}}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/519d77a6f894b5ebc9240b813a675477194f8858)
![{\displaystyle {\begin{aligned}\nombredeloperador {E} \left[\ln ^{2}(X)\right]&=(\psi (\alpha )-\psi (\alpha +\beta ))^{2}+\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta ),\\\nombredeloperador {E} \left[\ln ^{2}(1-X)\right]&=(\psi (\beta )-\psi (\alpha +\beta ))^{2}+\psi _{1}(\beta )-\psi _{1}(\alpha +\beta ),\\\nombredeloperador {E} \left[\ln(X)\ln(1-X)\right]&=(\psi (\alpha )-\psi (\alpha +\beta ))(\psi (\beta )-\psi (\alpha +\beta ))-\psi _{1}(\alpha +\beta ).\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42eb1276e349df39df3051df11e0e16afe88e2e)
![{\displaystyle {\begin{aligned}\operatorname {cov} [\ln(X),\ln(1-X)]&=\operatorname {E} \left[\ln(X)\ln(1-X)\right]-\operatorname {E} [\ln(X)]\operatorname {E} [\ln(1-X)]=-\psi _{1}(\alpha +\beta )\\&\\\operatorname {var} [\ln X]&=\operatorname {E} [\ln ^{2}(X)]-(\operatorname {E} [\ln(X)])^{2}\\&=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )\\&=\psi _{1}(\alpha )+\operatorname {cov} [\ln(X),\ln(1-X)]\\&\\\nombredeloperador {var} [\ln(1-X)]&=\nombredeloperador {E} [\ln ^{2}(1-X)]-(\nombredeloperador {E} [\ln(1-X)])^{2}\\&=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )\\&=\psi _{1}(\beta )+\nombredeloperador {cov} [\ln(X),\ln(1-X)]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e76df52180954247e1d1aa62646a20f7e3d68a36)

![{\displaystyle {\begin{aligned}\operatorname {var} \left[\ln \left({\frac {1}{X}}\right)\right]&=\operatorname {var} [\ln(X)]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta ),\\\operatorname {var} \left[\ln \left({\frac {1}{1-X}}\right)\right]&=\operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta ),\\\operatorname {cov} \left[\ln \left({\frac {1}{X}}\right),\ln \left({\frac {1}{1-X}}\right)\right]&=\operatorname {cov} [\ln(X),\ln(1-X)]=-\psi _{1}(\alpha +\beta ).\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d335167cf1713083b3fb1c4d0cfadb04c1d40d43)
![{\displaystyle \operatorname {var} \left[\ln \left({\frac {X}{1-X}}\right)\right]=\operatorname {var} \left[\ln \left({\frac {1-X}{X}}\right)\right]=-\operatorname {cov} \left[\ln \left({\frac {X}{1-X}}\right),\ln \left({\frac {1-X}{X}}\right)\right]=\psi _{1}(\alpha )+\psi _{1}(\beta ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52585d88405196366b14e2e7183f48be9b5de874)
![{\displaystyle {\begin{aligned}h(X)&=\operatorname {E} [-\ln(f(x;\alpha ,\beta ))]\\[4pt]&=\int _{0}^{1}-f(x;\alpha ,\beta )\ln(f(x;\alpha ,\beta ))\,dx\\[4pt]&=\ln(\mathrm {B} (\alpha ,\beta ))-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )+(\alpha +\beta -2)\psi (\alpha +\beta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc995dbbf41c91536ce4d0efaff554d8b0a77fe)




![{\displaystyle {\begin{aligned}H(X_{1},X_{2})&=\int _{0}^{1}-f(x;\alpha ,\beta )\ln(f(x;\alpha ',\beta '))\,dx\\[4pt]&=\ln \left(\mathrm {B} (\alpha ',\beta ')\right)-(\alpha '-1)\psi (\alpha )-(\beta '-1)\psi (\beta )+(\alpha '+\beta '-2)\psi (\alpha +\beta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711e6ef61e56ccd8ba515b8db5013d1847939ec8)
![{\displaystyle {\begin{aligned}D_{\mathrm {KL} }(X_{1}\parallel X_{2})&=\int _{0}^{1}f(x;\alpha ,\beta )\ln \left({\frac {f(x;\alpha ,\beta )}{f(x;\alpha ',\beta ')}}\right)\,dx\\[4pt]&=\left(\int _{0}^{1}f(x;\alpha ,\beta )\ln(f(x;\alpha ,\beta ))\,dx\right)-\left(\int _{0}^{1}f(x;\alpha ,\beta )\ln(f(x;\alpha ',\beta '))\,dx\right)\\[4pt]&=-h(X_{1})+H(X_{1},X_{2})\\[4pt]&=\ln \left({\frac {\mathrm {B} (\alpha ',\beta ')}{\mathrm {B} (\alpha ,\beta )}}\right)+(\alpha -\alpha ')\psi (\alpha )+(\beta -\beta ')\psi (\beta )+(\alpha '-\alpha +\beta '-\beta )\psi (\alpha +\beta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d62cb13ae214eaa48e12d453fbae8bdd58b301a)


















![{\displaystyle \operatorname {E} [|XE[X]|](\mathrm {B} (\alpha ,\beta ))=\operatorname {E} [|XE[X]|](\mathrm {B} (\beta,\alfa))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83468b7365d9095b07e04bfbb5c9cff50c64ea2d)


![{\displaystyle {\text{Re}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)]={\text{Re}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;-it)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bbddff6ec53eb39eccc603618459ba36e10ad2)
![{\displaystyle {\text{Im}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)]=-{\text{Im}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;-it)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebb682c9915a60ef8d982340de042127ab262a0f)
![{\displaystyle {\text{Abs}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;it)]={\text{Abs}}[{}_{1}F_{1}(\alpha ;\alpha +\beta ;-it)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c1c15ff4c63020b66d2404d439514d965946d0)





































































































![{\displaystyle \operatorname {var} [\ln(X)]=\operatorname {E} [\ln ^{2}(X)]-(\operatorname {E} [\ln(X)])^{2}=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7737d681fea7490e27f8760c6bcc8fccb154904)
![{\displaystyle \operatorname {var} [\ln(1-X)]=\operatorname {E} [\ln ^{2}(1-X)]-(\operatorname {E} [\ln(1-X)])^{2}=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f84c3747955206cf2190c61bd7875a6cd739ac04)
![{\displaystyle \nombreoperador {var} [\ln(X)]>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fb5a5d0db057469fb9dad8df2902fe93e3f3b0d)
![{\displaystyle \nombreoperador {var} [\ln(1-X)]>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c66a5aaa8362f578beb9b141b4108138b9d21e89)



![{\displaystyle {\begin{aligned}{\hat {\operatorname {E} }}[\ln(X)]&=\psi ({\hat {\alpha }})-\psi ({\hat {\alpha }}+{\hat {\beta }})={\frac {1}{N}}\sum _{i=1}^{N}\ln X_{i}=\ln {\hat {G}}_{X}\\{\hat {\operatorname {E} }}[\ln(1-X)]&=\psi ({\hat {\beta }})-\psi ({\hat {\alpha }}+{\hat {\beta }})={\frac {1}{N}}\sum _{i=1}^{N}\ln(1-X_{i})=\ln {\hat {G}}_{(1-X)}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e43bfd770a92437c9b0bbef4c7c6ead3534eba3)













![{\displaystyle {\hat {\operatorname {E} }}\left[\ln \left({\frac {X}{1-X}}\right)\right]=\psi ({\hat {\alpha }})-\psi ({\hat {\beta }})={\frac {1}{N}}\sum _{i=1}^{N}\ln {\frac {X_{i}}{1-X_{i}}}=\ln {\hat {G}}_{X}-\ln \left({\hat {G}}_{(1-X)}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d5d9a3105854f3fe65f5a72aa4418da4a50ba11)












![{\displaystyle {\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{\partial \alpha ^{2}}}=-\operatorname {var} [\ln X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/517a09a3b13d22689a3e1e400cbcab3af08e130c)
![{\displaystyle {\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{\partial \beta ^{2}}}=-\operatorname {var} [\ln(1-X)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1715f50fc408ceba307005a3f9e404520edd5a20)
![{\displaystyle \mathrm {var} ({\hat {\alpha }})\geq {\frac {1}{\operatorname {var} [\ln X]}}\geq {\frac {1}{\psi _{1}({\hat {\alpha }})-\psi _{1}({\hat {\alpha }}+{\hat {\beta }})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/744f1e8421337ed7a2e6cae00fccec1eaf68e3dc)
![{\displaystyle \mathrm {var} ({\hat {\beta }})\geq {\frac {1}{\operatorname {var} [\ln(1-X)]}}\geq {\frac {1 }{\psi _{1}({\hat {\beta }})-\psi _{1}({\hat {\alpha }}+{\hat {\beta }})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f01dc5c3eb614cfa71a500fd34f3fa430c183c76)















![{\displaystyle \alpha =2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial a^{2}}}\right]={\mathcal {I}}_{a,a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53538160a2404a5d7b74ae2033fbbb2dbc1045eb)
![{\displaystyle \beta =2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial c^{2}}}\right]={\mathcal {I}}_{c,c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee2c6ecfcafe60e54799ab4a16451cf478d65f7d)
![{\displaystyle \alpha =2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha \partial a}}\right]={\mathcal {I}}_{\alpha ,a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b8af544d7c5e0cc278aa725daba7f3de2f70d31)
![{\displaystyle \beta =1:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \beta \partial c}}\right]={\mathcal {I}}_{\beta ,c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f87b32b39997964dcbc95bc64c1364e6832db1d)
![{\displaystyle {\mathcal {I}}(\alpha )=\operatorname {E} \left[\left({\frac {\partial }{\partial \alpha }}\ln {\mathcal {L}}(\alpha \mid X)\right)^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daec13972d17a073bcd447abfde55a6b0e168720)
![{\displaystyle {\mathcal {I}}(\alpha )=-\operatorname {E} \left[{\frac {\partial ^{2}}{\partial \alpha ^{2}}}\ln({\mathcal {L}}(\alpha \mid X))\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92244569d1fab7e801097aa25a9c883ff75be5aa)
![{\displaystyle \operatorname {var} [{\hat {\alpha }}]\geq {\frac {1}{{\mathcal {I}}(\alpha )}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d93d4983a2717258c52eb47d1562e849a3a66c5c)

![{\displaystyle ({\mathcal {I}}(\theta ))_{i,j}=\operatorname {E} \left[\left({\frac {\partial }{\partial \theta _{i}}}\ln {\mathcal {L}}\right)\left({\frac {\partial }{\partial \theta _{j}}}\ln {\mathcal {L}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e4390c2c908fe7a3e4f06ee9e3526df1ff20f18)
![{\displaystyle ({\mathcal {I}}(\theta ))_{i,j}=-\operatorname {E} \left[{\frac {\partial ^{2}}{\partial \theta _{i}\,\partial \theta _{j}}}\ln({\mathcal {L}})\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b7d9fd3ec7fa358ec6450f166aa89592bcc55ab)


![{\displaystyle -{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\partial \alpha ^{2}}}=\operatorname {var} [\ln(X)]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\alpha ,\alpha }=\operatorname {E} \left[-{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\partial \alpha ^{2}}}\right]=\ln \operatorname {var} _{GX}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c90003d5bd2f6d2bcfe2c788585689726b4b7e36)
![{\displaystyle -{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\,\partial \beta ^{2}}}=\operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\beta ,\beta }=\operatorname {E} \left[-{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\partial \beta ^{2}}}\right]=\ln \operatorname {var} _{G(1-X)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59bcc31f14f1f4b3b07bd92a66426bb6ac126b1)
![{\displaystyle -{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\,\partial \alpha \,\partial \beta }}=\operatorname {cov} [\ln X,\ln(1-X)]=-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\alpha ,\beta }=\operatorname {E} \left[-{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta \mid X)}{N\,\partial \alpha \,\partial \beta }}\right]=\ln \operatorname {cov} _{G{X,(1-X)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c3268da3b23c062ce981ab02d4c454a0267365)




![{\displaystyle {\begin{aligned}\det({\mathcal {I}}(\alpha ,\beta ))&={\mathcal {I}}_{\alpha ,\alpha }{\mathcal {I}}_{\beta ,\beta }-{\mathcal {I}}_{\alpha ,\beta }{\mathcal {I}}_{\alpha ,\beta }\\[4pt]&=(\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta ))(\psi _{1}(\beta )-\psi _{1}(\alpha +\beta ))-(-\psi _{1}(\alpha +\beta ))(-\psi _{1}(\alpha +\beta ))\\[4pt]&=\psi _{1}(\alpha )\psi _{1}(\beta )-(\psi _{1}(\alpha )+\psi _{1}(\beta ))\psi _{1}(\alpha +\beta )\\[4pt]\lim _{\alpha \to 0}\det({\mathcal {I}}(\alpha ,\beta ))&=\lim _{\beta \to 0}\det({\mathcal {I}}(\alpha ,\beta ))=\infty \\[4pt]\lim _{\alpha \to \infty }\det({\mathcal {I}}(\alpha ,\beta ))&=\lim _{\beta \to \infty }\det({\mathcal {I}}(\alpha ,\beta ))=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2c5ccf59b05ea730fc108360c07e9ac9634e829)

![{\displaystyle -{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha ^{2}}}=\operatorname {var} [\ln(X)]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\alpha ,\alpha }=\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha ^{2}}}\right]=\ln(\operatorname {var_{GX}} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31be86f2c53663c6d3975bc2676806ba3e538423)
![{\displaystyle -{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \beta ^{2}}}=\operatorname {var} [\ln(1-X)]=\psi _{1}(\beta )-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\beta ,\beta }=\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \beta ^{2}}}\right]=\ln(\operatorname {var_{G(1-X)}} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ab885119f25fae0b9919326db96395d13e3bc3)
![{\displaystyle -{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha \,\partial \beta }}=\operatorname {cov} [\ln X,(1-X)]=-\psi _{1}(\alpha +\beta )={\mathcal {I}}_{\alpha ,\beta }=\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha \,\partial \beta }}\right]=\ln(\operatorname {cov} _{G{X,(1-X)}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02a56af746fb9315340cf382951fe0c3f3640678)

![{\displaystyle {\begin{aligned}\alpha >2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial a^{2}}}\right]&={\mathcal {I}}_{a,a}={\frac {\beta (\alpha +\beta -1)}{(\alpha -2)(c-a)^{2}}}\\\beta >2:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial c^{2}}}\right]&={\mathcal {I}}_{c,c}={\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(c-a)^{2}}}\\\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial a\,\partial c}}\right]&={\mathcal {I}}_{a,c}={\frac {(\alpha +\beta -1)}{(c-a)^{2}}}\\\alpha >1:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha \,\partial a}}\right]&={\mathcal {I}}_{\alpha ,a}={\frac {\beta }{(\alpha -1)(c-a)}}\\\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \alpha \,\partial c}}\right]&={\mathcal {I}}_{\alpha ,c}={\frac {1}{(c-a)}}\\\operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \beta \,\partial a}}\right]&={\mathcal {I}}_{\beta ,a}=-{\frac {1}{(c-a)}}\\\beta >1:\quad \operatorname {E} \left[-{\frac {1}{N}}{\frac {\partial ^{2}\ln {\mathcal {L}}(\alpha ,\beta ,a,c\mid Y)}{\partial \beta \,\partial c}}\right]&={\mathcal {I}}_{\beta ,c}=-{\frac {\alpha }{(\beta -1)(c-a)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/636646f51bdb1a3193b1721483878e98f4f19c3e)




![{\displaystyle {\mathcal {I}}_{\alpha ,a}={\frac {\operatorname {E} \left[{\frac {1-X}{X}}\right]}{c-a}}={\frac {\beta }{(\alpha -1)(c-a)}}{\text{ if }}\alpha >1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e670565bb8d06bace69cf892864520f5c83b5449)
![{\displaystyle {\mathcal {I}}_{\beta ,c}=-{\frac {\operatorname {E} \left[{\frac {X}{1-X}}\right]}{c-a}}=-{\frac {\alpha }{(\beta -1)(c-a)}}{\text{ if }}\beta >1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94f9b7788a4f19e1cbc765ab8fc85a7ad55dec4f)
![{\displaystyle {\begin{aligned}\alpha >2:\quad {\mathcal {I}}_{a,a}&=\operatorname {var} \left[{\frac {1}{X}}\right]\left({\frac {\alpha -1}{c-a}}\right)^{2}=\operatorname {var} \left[{\frac {1-X}{X}}\right]\left({\frac {\alpha -1}{c-a}}\right)^{2}={\frac {\beta (\alpha +\beta -1)}{(\alpha -2)(c-a)^{2}}}\\\beta >2:\quad {\mathcal {I}}_{c,c}&=\operatorname {var} \left[{\frac {1}{1-X}}\right]\left({\frac {\beta -1}{c-a}}\right)^{2}=\operatorname {var} \left[{\frac {X}{1-X}}\right]\left({\frac {\beta -1}{c-a}}\right)^{2}={\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(c-a)^{2}}}\\{\mathcal {I}}_{a,c}&=\operatorname {cov} \left[{\frac {1}{X}},{\frac {1}{1-X}}\right]{\frac {(\alpha -1)(\beta -1)}{(c-a)^{2}}}=\operatorname {cov} \left[{\frac {1-X}{X}},{\frac {X}{1-X}}\right]{\frac {(\alpha -1)(\beta -1)}{(c-a)^{2}}}={\frac {(\alpha +\beta -1)}{(c-a)^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f89730020364bb58791ca0eb47d0de25c896c2)








![{\displaystyle {\begin{aligned}{\sqrt {{\mathcal {I}}(p)}}&={\sqrt {\operatorname {E} \!\left[\left({\frac {d}{dp}}\ln({\mathcal {L}}(p\mid H))\right)^{2}\right]}}\\[6pt]&={\sqrt {\operatorname {E} \!\left[\left({\frac {H}{p}}-{\frac {1-H}{1-p}}\right)^{2}\right]}}\\[6pt]&={\sqrt {p^{1}(1-p)^{0}\left({\frac {1}{p}}-{\frac {0}{1-p}}\right)^{2}+p^{0}(1-p)^{1}\left({\frac {0}{p}}-{\frac {1}{1-p}}\right)^{2}}}\\&={\frac {1}{\sqrt {p(1-p)}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/324e2e5a963eed1652cf2d3a9ba95e5491b5df95)







![{\displaystyle {\begin{aligned}&{\text{posterior probability density}}(x=p\mid s,n-s)\\[6pt]={}&{\frac {\operatorname {priorprobabilitydensity} (x=p;\alpha \operatorname {prior} ,\beta \operatorname {prior} ){\mathcal {L}}(s,f\mid x=p)}{\int _{0}^{1}{\text{prior probability density}}(x=p;\alpha \operatorname {prior} ,\beta \operatorname {prior} ){\mathcal {L}}(s,f\mid x=p)\,dx}}\\[6pt]={}&{\frac {{n \choose s}x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}/\mathrm {B} (\alpha \operatorname {prior} ,\beta \operatorname {prior} )}{\int _{0}^{1}\left({n \choose s}x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}/\mathrm {B} (\alpha \operatorname {prior} ,\beta \operatorname {prior} )\right)\,dx}}\\[6pt]={}&{\frac {x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}}{\int _{0}^{1}\left(x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}\right)\,dx}}\\[6pt]={}&{\frac {x^{s+\alpha \operatorname {prior} -1}(1-x)^{n-s+\beta \operatorname {prior} -1}}{\mathrm {B} (s+\alpha \operatorname {prior} ,n-s+\beta \operatorname {prior} )}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/569ad0317cf545ff98538c8a845f216120e87c08)














![{\displaystyle {\begin{aligned}\mu (X)&={\frac {a+4b+c}{6}}\\[8pt]\sigma (X)&={\frac {c-a}{6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a89a68d1250ebe659be15e88edb5a9eb3e0cf87)




























