Distribución de arcoseno
Tipo de distribución de probabilidad
Arcoseno
Función de densidad de probabilidad
Función de densidad de probabilidad para la distribución de arcoseno
Función de distribución acumulativa
Función de distribución acumulativa 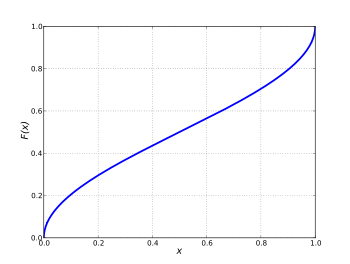para la distribución de arcoseno
Parámetrosninguno
Apoyo incógnita ∈ [ 0 , 1 ] {\displaystyle x\en [0,1]}
PDF F ( incógnita ) = 1 π incógnita ( 1 − incógnita ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}
CDF F ( incógnita ) = 2 π arcoseno ⁡ ( incógnita ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)}
Significar 1 2 {\displaystyle {\frac {1}{2}}}
Mediana 1 2 {\displaystyle {\frac {1}{2}}}
Modo x ∈ { 0 , 1 } {\displaystyle x\in \{0,1\}}
Diferencia 1 8 {\displaystyle {\tfrac {1}{8}}}
Oblicuidad 0 {\displaystyle 0}
Exceso de curtosis − 3 2 {\displaystyle -{\tfrac {3}{2}}}
Entropía ln ⁡ π 4 {\displaystyle \ln {\tfrac {\pi }{4}}}
MGF 1 + ∑ k = 1 ∞ ( ∏ r = 0 k − 1 2 r + 1 2 r + 2 ) t k k ! {\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {2r+1}{2r+2}}\right){\frac {t^{k}}{k!}}}
CF e i t 2 J 0 ( t 2 ) {\displaystyle e^{i{\frac {t}{2}}}J_{0}({\frac {t}{2}})}

En teoría de probabilidad , la distribución arcoseno es la distribución de probabilidad cuya función de distribución acumulativa involucra el arcoseno y la raíz cuadrada :

F ( x ) = 2 π arcsin ⁡ ( x ) = arcsin ⁡ ( 2 x − 1 ) π + 1 2 {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}}}

para 0 ≤  x  ≤ 1, y cuya función de densidad de probabilidad es

f ( x ) = 1 π x ( 1 − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}

en (0, 1). La distribución de arcoseno estándar es un caso especial de la distribución beta con α  =  β  = 1/2. Es decir, si es una variable aleatoria distribuida según un arcoseno, entonces . Por extensión, la distribución de arcoseno es un caso especial de la distribución de tipo I de Pearson . X {\displaystyle X} X ∼ B e t a ( 1 2 , 1 2 ) {\displaystyle X\sim {\rm {Beta}}{\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}}

La distribución de arcoseno aparece en la ley de arcoseno de Lévy , en la ley de arcoseno de Erdős y como la distribución previa de Jeffreys para la probabilidad de éxito de un ensayo de Bernoulli . [1] [2]

Generalización

Arcoseno – soporte acotado
Parámetros − ∞ < a < b < ∞ {\displaystyle -\infty <a<b<\infty \,}
Apoyo x ∈ [ a , b ] {\displaystyle x\in [a,b]}
PDF f ( x ) = 1 π ( x − a ) ( b − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}
CDF F ( x ) = 2 π arcsin ⁡ ( x − a b − a ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}
Significar a + b 2 {\displaystyle {\frac {a+b}{2}}}
Mediana a + b 2 {\displaystyle {\frac {a+b}{2}}}
Modo x ∈ a , b {\displaystyle x\in {a,b}}
Diferencia 1 8 ( b − a ) 2 {\displaystyle {\tfrac {1}{8}}(b-a)^{2}}
Oblicuidad 0 {\displaystyle 0}
Exceso de curtosis − 3 2 {\displaystyle -{\tfrac {3}{2}}}
CF e i t b + a 2 J 0 ( b − a 2 t ) {\displaystyle e^{it{\frac {b+a}{2}}}J_{0}({\frac {b-a}{2}}t)}

Soporte arbitrario y limitado

La distribución se puede ampliar para incluir cualquier soporte acotado de a  ≤  x  ≤  b mediante una transformación simple

F ( x ) = 2 π arcsin ⁡ ( x − a b − a ) {\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}

para a  ≤  x  ≤  b , y cuya función de densidad de probabilidad es

f ( x ) = 1 π ( x − a ) ( b − x ) {\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}

en ( a ,  b ).

Factor de forma

Distribución de arcoseno estándar generalizada en (0,1) con función de densidad de probabilidad

f ( x ; α ) = sin ⁡ π α π x − α ( 1 − x ) α − 1 {\displaystyle f(x;\alpha )={\frac {\sin \pi \alpha }{\pi }}x^{-\alpha }(1-x)^{\alpha -1}}

También es un caso especial de la distribución beta con parámetros . B e t a ( 1 − α , α ) {\displaystyle {\rm {Beta}}(1-\alpha ,\alpha )}

Tenga en cuenta que cuando la distribución general del arcoseno se reduce a la distribución estándar mencionada anteriormente. α = 1 2 {\displaystyle \alpha ={\tfrac {1}{2}}}

Propiedades

  • La distribución de arcoseno está cerrada bajo traslación y escala por un factor positivo
    • Si X ∼ A r c s i n e ( a , b )   then  k X + c ∼ A r c s i n e ( a k + c , b k + c ) {\displaystyle X\sim {\rm {Arcsine}}(a,b)\ {\text{then }}kX+c\sim {\rm {Arcsine}}(ak+c,bk+c)}
  • El cuadrado de una distribución de arcoseno sobre (-1, 1) tiene una distribución de arcoseno sobre (0, 1)
    • Si X ∼ A r c s i n e ( − 1 , 1 )   then  X 2 ∼ A r c s i n e ( 0 , 1 ) {\displaystyle X\sim {\rm {Arcsine}}(-1,1)\ {\text{then }}X^{2}\sim {\rm {Arcsine}}(0,1)}
  • Las coordenadas de puntos seleccionados uniformemente en un círculo de radio centrado en el origen (0, 0), tienen una distribución r {\displaystyle r} A r c s i n e ( − r , r ) {\displaystyle {\rm {Arcsine}}(-r,r)}
    • Por ejemplo, si seleccionamos un punto uniformemente en la circunferencia, , tenemos que la distribución de coordenadas x del punto es , y su distribución de coordenadas y es U ∼ U n i f o r m ( 0 , 2 π r ) {\displaystyle U\sim {\rm {Uniform}}(0,2\pi r)} r ⋅ cos ⁡ ( U ) ∼ A r c s i n e ( − r , r ) {\displaystyle r\cdot \cos(U)\sim {\rm {Arcsine}}(-r,r)} r ⋅ sin ⁡ ( U ) ∼ A r c s i n e ( − r , r ) {\textstyle r\cdot \sin(U)\sim {\rm {Arcsine}}(-r,r)}

Función característica

La función característica de la distribución de arcoseno generalizada es una función de Bessel de orden cero de primera especie, multiplicada por una exponencial compleja, dada por . Para el caso especial de , la función característica toma la forma de . e i t b + a 2 J 0 ( b − a 2 t ) {\displaystyle e^{it{\frac {b+a}{2}}}J_{0}({\frac {b-a}{2}}t)} b = − a {\displaystyle b=-a} J 0 ( b t ) {\displaystyle J_{0}(bt)}

  • Si U y V son variables aleatorias uniformes iid ( −π,π), entonces , , y todos tienen una distribución. sin ⁡ ( U ) {\displaystyle \sin(U)} sin ⁡ ( 2 U ) {\displaystyle \sin(2U)} − cos ⁡ ( 2 U ) {\displaystyle -\cos(2U)} sin ⁡ ( U + V ) {\displaystyle \sin(U+V)} sin ⁡ ( U − V ) {\displaystyle \sin(U-V)} A r c s i n e ( − 1 , 1 ) {\displaystyle {\rm {Arcsine}}(-1,1)}
  • Si la distribución de arcoseno generalizada con parámetro de forma se apoya en el intervalo finito [a,b] entonces X {\displaystyle X} α {\displaystyle \alpha } X − a b − a ∼ B e t a ( 1 − α , α )   {\displaystyle {\frac {X-a}{b-a}}\sim {\rm {Beta}}(1-\alpha ,\alpha )\ }
  • Si X ~ Cauchy(0, 1) entonces tiene una distribución de arcoseno estándar 1 1 + X 2 {\displaystyle {\tfrac {1}{1+X^{2}}}}

Referencias

  1. ^ Overturf, Drew; et al. (2017). Investigación de patrones de formación de haces a partir de matrices en fase distribuidas volumétricamente . MILCOM 2017 - Conferencia de Comunicaciones Militares IEEE 2017 (MILCOM). págs. 817–822. doi :10.1109/MILCOM.2017.8170756. ISBN 978-1-5386-0595-0.
  2. ^ Buchanan, K.; et al. (2020). "Orientación de haz nulo mediante matrices distribuidas y distribuciones de apertura compartida". Transacciones IEEE sobre antenas y propagación . 68 (7): 5353–5364. doi :10.1109/TAP.2020.2978887.

Lectura adicional

Retrieved from "https://en.wikipedia.org/w/index.php?title=Arcsine_distribution&oldid=1251766937"