Distribución triangular
Distribución de probabilidad
Triangular
Función de densidad de probabilidad
Trazado del PMF triangular
Función de distribución acumulativa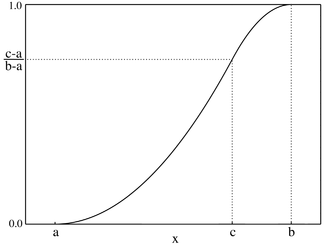
Trazado del CMF triangular
Parámetros a :   a ∈ ( − ∞ , ∞ ) {\displaystyle a:~a\in (-\infty ,\infty )}
b :   a < b {\estilo de visualización b:~a<b\,}
do :   a ≤ do ≤ b {\displaystyle c:~a\leq c\leq b\,}
Apoyo a ≤ incógnita ≤ b {\displaystyle a\leq x\leq b\!}
PDF { 0 para  incógnita < a , 2 ( incógnita − a ) ( b − a ) ( do − a ) para  a ≤ incógnita < do , 2 b − a para  incógnita = do , 2 ( b − incógnita ) ( b − a ) ( b − do ) para  do < incógnita ≤ b , 0 para  b < incógnita . {\displaystyle {\begin{cases}0&{\text{para }}x<a,\\{\frac {2(xa)}{(ba)(ca)}}&{\text{para }}a\leq x<c,\\[4pt]{\frac {2}{ba}}&{\text{para }}x=c,\\[4pt]{\frac {2(bx)}{(ba)(bc)}}&{\text{para }}c<x\leq b,\\[4pt]0&{\text{para }}b<x.\end{cases}}}
CDF { 0 para  incógnita ≤ a , ( incógnita − a ) 2 ( b − a ) ( do − a ) para  a < incógnita ≤ do , 1 − ( b − incógnita ) 2 ( b − a ) ( b − do ) para  do < incógnita < b , 1 para  b ≤ incógnita . {\displaystyle {\begin{cases}0&{\text{para }}x\leq a,\\[2pt]{\frac {(xa)^{2}}{(ba)(ca)}}&{\text{para }}a<x\leq c,\\[4pt]1-{\frac {(bx)^{2}}{(ba)(bc)}}&{\text{para }}c<x<b,\\[4pt]1&{\text{para }}b\leq x.\end{cases}}}
Significar a + b + do 3 {\displaystyle {\frac {a+b+c}{3}}}
Mediana { a + ( b − a ) ( do − a ) 2 para  do ≥ a + b 2 , b − ( b − a ) ( b − do ) 2 para  do ≤ a + b 2 . {\displaystyle {\begin{cases}a+{\sqrt {\frac {(ba)(ca)}{2}}}&{\text{para }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(ba)(bc)}{2}}}&{\text{para }}c\leq {\frac {a+b}{2}}.\end{cases}}}
Modo do {\estilo de visualización c\,}
Diferencia a 2 + b 2 + do 2 − a b − a do − b do 18 {\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
Oblicuidad 2 ( a + b − 2 do ) ( 2 a − b − do ) ( a − 2 b + do ) 5 ( a 2 + b 2 + do 2 − a b − a do − b do ) 3 2 {\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}
Exceso de curtosis − 3 5 {\displaystyle -{\frac {3}{5}}}
Entropía 1 2 + En ⁡ ( b − a 2 ) {\displaystyle {\frac {1}{2}}+\ln \left({\frac {ba}{2}}\right)}
MGF 2 ( b − do ) mi a a − ( b − a ) mi do a + ( do − a ) mi b a ( b − a ) ( do − a ) ( b − do ) a 2 {\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(ba)(ca)(bc)t^{2}}}}
CF − 2 ( b − do ) mi i a a − ( b − a ) mi i do a + ( do − a ) mi i b a ( b − a ) ( do − a ) ( b − do ) a 2 {\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(ba)(ca)(bc)t^{2}}}}

En teoría de probabilidad y estadística , la distribución triangular es una distribución de probabilidad continua con límite inferior a , límite superior b y modo c , donde a  <  b y a  ≤  c  ≤  b .

Casos especiales

La moda en un límite

La distribución se simplifica cuando c  =  a o c  =  b . Por ejemplo, si a  = 0, b  = 1 y c  = 1, entonces la PDF y la CDF se convierten en:

F ( incógnita ) = 2 incógnita F ( incógnita ) = incógnita 2 }  para  0 ≤ incógnita ≤ 1 {\displaystyle \left.{\begin{array}{rl}f(x)&=2x\\[8pt]F(x)&=x^{2}\end{array}}\right\}{\text{ para }}0\leq x\leq 1}
mi ⁡ ( incógnita ) = 2 3 Variedad ⁡ ( incógnita ) = 1 18 {\displaystyle {\begin{aligned}\operatorname {E} (X)&={\frac {2}{3}}\\[8pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}

Distribución de la diferencia absoluta de dos variables uniformes estándar

Esta distribución para a  = 0, b  = 1 y c  = 0 es la distribución de X  = | X 1  −  X 2 |, donde X 1 , X 2 son dos variables aleatorias independientes con distribución uniforme estándar .

F ( incógnita ) = 2 − 2 incógnita  para  0 ≤ incógnita < 1 F ( incógnita ) = 2 incógnita − incógnita 2  para  0 ≤ incógnita < 1 mi ( incógnita ) = 1 3 Variedad ⁡ ( incógnita ) = 1 18 {\displaystyle {\begin{aligned}f(x)&=2-2x{\text{ para }}0\leq x<1\\[6pt]F(x)&=2x-x^{2}{\text{ para }}0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}

Distribución triangular simétrica

El caso simétrico surge cuando c = ( a + b ) / 2. En este caso, una forma alternativa de la función de distribución es:

F ( incógnita ) = ( b − do ) − | do − incógnita | ( b − do ) 2 {\displaystyle {\begin{aligned}f(x)&={\frac {(bc)-|cx|}{(bc)^{2}}}\\[6pt]\end{aligned}}}

Distribución de la media de dos variables uniformes estándar

Esta distribución para a  = 0, b  = 1 y c  = 0,5—la moda (es decir, el pico) está exactamente en el medio del intervalo—corresponde a la distribución de la media de dos variables uniformes estándar, es decir, la distribución de X  = ( X 1  +  X 2 ) / 2, donde X 1 , X 2 son dos variables aleatorias independientes con distribución uniforme estándar en [0, 1]. [1] Es el caso de la distribución de Bates para dos variables.

F ( incógnita ) = { 4 incógnita para  0 ≤ incógnita < 1 2 4 ( 1 − incógnita ) para  1 2 ≤ incógnita ≤ 1 {\displaystyle f(x)={\begin{cases}4x&{\text{para }}0\leq x<{\frac {1}{2}}\\4(1-x)&{\text{para }}{\frac {1}{2}}\leq x\leq 1\end{cases}}}
F ( incógnita ) = { 2 incógnita 2 para  0 ≤ incógnita < 1 2 2 incógnita 2 − ( 2 incógnita − 1 ) 2 para  1 2 ≤ incógnita ≤ 1 {\displaystyle F(x)={\begin{cases}2x^{2}&{\text{para }}0\leq x<{\frac {1}{2}}\\2x^{2}-(2x-1)^{2}&{\text{para }}{\frac {1}{2}}\leq x\leq 1\end{cases}}}
mi ( incógnita ) = 1 2 Variedad ⁡ ( incógnita ) = 1 24 {\displaystyle {\begin{aligned}E(X)&={\frac {1}{2}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{24}}\end{aligned}}}

Generando variables aleatorias

Dada una variable aleatoria U extraída de la distribución uniforme en el intervalo (0, 1), entonces la variable

incógnita = { a + tú ( b − a ) ( do − a )  para  0 < tú < F ( do ) b − ( 1 − tú ) ( b − a ) ( b − do )  para  F ( do ) ≤ tú < 1 {\displaystyle X={\begin{cases}a+{\sqrt {U(ba)(ca)}}&{\text{ para }}0<U<F(c)\\&\\b-{\sqrt {(1-U)(ba)(bc)}}&{\text{ para }}F(c)\leq U<1\end{cases}}} [2]

donde , tiene una distribución triangular con parámetros y . Esto se puede obtener a partir de la función de distribución acumulativa. F ( do ) = ( do − a ) / ( b − a ) {\displaystyle F(c)=(ca)/(ba)} a , b {\estilo de visualización a,b} do {\estilo de visualización c}

Uso de la distribución

La distribución triangular se utiliza normalmente como descripción subjetiva de una población para la que sólo hay datos de muestra limitados, y especialmente en casos en los que se conoce la relación entre las variables pero los datos son escasos (posiblemente debido al alto coste de la recogida). Se basa en el conocimiento del mínimo y el máximo y en una "conjetura inspirada" [3] sobre el valor modal. Por estos motivos, la distribución triangular se ha denominado distribución de "falta de conocimiento".

Simulaciones de negocios

Por lo tanto, la distribución triangular se utiliza a menudo en la toma de decisiones empresariales , en particular en las simulaciones . Por lo general, cuando no se sabe mucho sobre la distribución de un resultado (por ejemplo, solo sus valores más pequeños y más grandes), es posible utilizar la distribución uniforme . Pero si también se conoce el resultado más probable, entonces el resultado puede simularse mediante una distribución triangular. Véase, por ejemplo, en finanzas corporativas .

Gestión de proyectos

La distribución triangular, junto con la distribución PERT , también se utiliza ampliamente en la gestión de proyectos (como entrada al PERT y, por lo tanto, al método de la ruta crítica (CPM)) para modelar eventos que tienen lugar dentro de un intervalo definido por un valor mínimo y máximo.

Dithering de audio

La distribución triangular simétrica se utiliza comúnmente en el tramado de audio , donde se denomina TPDF (función de densidad de probabilidad triangular).

Véase también

  • Distribución trapezoidal
  • Thomas Simpson
  • Estimación de tres puntos
  • Resumen de cinco números
  • Resumen de siete números
  • Función triangular
  • Teorema del límite central : la distribución triangular suele producirse como resultado de sumar dos variables aleatorias uniformes. En otras palabras, la distribución triangular suele ser (no siempre) el resultado de la primera iteración del proceso de suma del teorema del límite central (es decir, ). En este sentido, la distribución triangular puede producirse de forma natural ocasionalmente. Si este proceso de sumar más variables aleatorias continúa (es decir, ), la distribución adquirirá cada vez más forma de campana. norte = 2 {\textstyle n=2} norte ≥ 3 {\textstyle n\geq 3}
  • Distribución de Irwin-Hall : utilizar una distribución de Irwin-Hall es una forma sencilla de generar una distribución triangular.
  • Distribución de Bates : similar a la distribución de Irwin-Hall, pero con valores reescalados dentro del rango de 0 a 1. Útil para el cálculo de una distribución triangular que posteriormente se puede reescalar y desplazar para crear otras distribuciones triangulares fuera del rango de 0 a 1.

Referencias

  1. ^ Kotz, Samuel; Dorp, Johan Rene Van (8 de diciembre de 2004). Más allá de Beta: otras familias continuas de distribuciones con soporte limitado y aplicaciones. World Scientific. ISBN 978-981-4481-24-3.
  2. ^ "Copia archivada" (PDF) . www.asianscientist.com . Archivado desde el original (PDF) el 7 de abril de 2014 . Consultado el 12 de enero de 2022 .{{cite web}}: CS1 maint: copia archivada como título ( enlace )
  3. ^ "Copia archivada" (PDF) . Archivado desde el original (PDF) el 23 de septiembre de 2006. Consultado el 23 de septiembre de 2006 .{{cite web}}: CS1 maint: copia archivada como título ( enlace )
  • Weisstein, Eric W. "Distribución triangular". MathWorld .
  • Distribución triangular, decisionsciences.org
  • Distribución triangular, brighton-webs.co.uk
  • Prueba de la varianza de la distribución triangular, math.stackexchange.com
Retrieved from "https://en.wikipedia.org/w/index.php?title=Triangular_distribution&oldid=1217239505"