Distribución uniforme continua

Uniforme continuo

Función de densidad de probabilidad 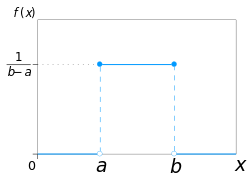Utilizando la convención máxima
Función de distribución acumulativa
Notación	${\displaystyle {\mathcal {U}}_{[a,b]}}$
Parámetros	${\displaystyle -\infty <a<b<\infty}$
Apoyo	${\estilo de visualización [a,b]}$
PDF	${\displaystyle {\begin{cases}{\frac {1}{ba}}&{\text{para }}x\en [a,b]\\0&{\text{en caso contrario}}\end{cases}}}$
CDF	${\displaystyle {\begin{cases}0&{\text{para }}x<a\\{\frac {xa}{ba}}&{\text{para }}x\in [a,b]\\1&{\text{para }}x>b\end{cases}}}$
Significar	${\displaystyle {\tfrac {1}{2}}(a+b)}$
Mediana	${\displaystyle {\tfrac {1}{2}}(a+b)}$
Modo	${\displaystyle {\text{cualquier valor en }}(a,b)}$
Diferencia	${\displaystyle {\tfrac {1}{12}}(ba)^{2}}$
ENOJADO	${\displaystyle {\tfrac {1}{4}}(ba)}$
Oblicuidad	${\estilo de visualización 0}$
Exceso de curtosis	${\displaystyle -{\frac {6}{5}}}$
Entropía	${\displaystyle \log(ba)}$
MGF	${\displaystyle {\begin{casos}{\frac {\mathrm {e} ^{tb}-\mathrm {e} ^{ta}}{t(ba)}}&{\text{para }}t\ neq 0\\1&{\text{para }}t=0\end{casos}}}$
CF	${\displaystyle {\begin{cases}{\frac {\mathrm {e} ^{\mathrm {i} tb}-\mathrm {e} ^{\mathrm {i} ta}}{\mathrm {i} t(b-a)}}&{\text{for }}t\neq 0\\1&{\text{for }}t=0\end{cases}}}$

En teoría de probabilidad y estadística , las distribuciones uniformes continuas o distribuciones rectangulares son una familia de distribuciones de probabilidad simétricas . Dicha distribución describe un experimento en el que hay un resultado arbitrario que se encuentra entre ciertos límites. ^[1] Los límites están definidos por los parámetros y que son los valores mínimo y máximo. El intervalo puede ser cerrado (es decir, ) o abierto (es decir, ). ^[2] Por lo tanto, la distribución a menudo se abrevia donde significa distribución uniforme. ^[1] La diferencia entre los límites define la longitud del intervalo; todos los intervalos de la misma longitud en el soporte de la distribución son igualmente probables. Es la distribución de probabilidad de entropía máxima para una variable aleatoria sin otra restricción que la de que está contenida en el soporte de la distribución. ^[3]${\displaystyle a}$${\displaystyle b,}$${\displaystyle [a,b]}$${\displaystyle (a,b)}$${\displaystyle U(a,b),}$${\displaystyle U}$ ${\displaystyle X}$

La función de densidad de probabilidad de la distribución uniforme continua es

${\displaystyle f(x)={\begin{cases}{\frac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[8pt]0&{\text{for }}x<a\ {\text{ or }}\ x>b.\end{cases}}}$

Los valores de en los dos límites y normalmente no son importantes, porque no alteran el valor de en ningún intervalo ni de ni de ningún momento superior. A veces se eligen como cero, y a veces como Esto último es apropiado en el contexto de la estimación por el método de máxima verosimilitud . En el contexto del análisis de Fourier , se puede tomar el valor de o como porque entonces la transformada inversa de muchas transformadas integrales de esta función uniforme devolverá la función misma, en lugar de una función que es igual " casi en todas partes ", es decir, excepto en un conjunto de puntos con medida cero . Además, es coherente con la función de signo , que no tiene tal ambigüedad.${\displaystyle f(x)}$${\displaystyle a}$${\displaystyle b}$${\textstyle \int _{c}^{d}f(x)dx}$${\displaystyle [c,d],}$${\textstyle \int _{a}^{b}xf(x)dx,}$${\displaystyle {\tfrac {1}{b-a}}.}$${\displaystyle f(a)}$${\displaystyle f(b)}$${\displaystyle {\tfrac {1}{2(b-a)}},}$

Toda función de densidad de probabilidad se integra a , por lo que la función de densidad de probabilidad de la distribución uniforme continua se representa gráficamente como un rectángulo donde ⁠ ⁠ es la longitud de la base y ⁠ ⁠ es la altura. A medida que aumenta la longitud de la base, la altura (la densidad en cualquier valor particular dentro de los límites de la distribución) disminuye. ^[4]${\displaystyle 1,}$${\displaystyle b-a}$${\displaystyle {\tfrac {1}{b-a}}}$

En términos de media y varianza, la función de densidad de probabilidad de la distribución uniforme continua es${\displaystyle \mu }$${\displaystyle \sigma ^{2},}$

${\displaystyle f(x)={\begin{cases}{\frac {1}{2\sigma {\sqrt {3}}}}&{\text{for }}-\sigma {\sqrt {3}}\leq x-\mu \leq \sigma {\sqrt {3}},\\0&{\text{otherwise}}.\end{cases}}}$

La función de distribución acumulativa de la distribución uniforme continua es:

${\displaystyle F(x)={\begin{cases}0&{\text{for }}x<a,\\[8pt]{\frac {x-a}{b-a}}&{\text{for }}a\leq x\leq b,\\[8pt]1&{\text{for }}x>b.\end{cases}}}$

Su inversa es:

${\displaystyle F^{-1}(p)=a+p(b-a)\quad {\text{ for }}0<p<1.}$

En términos de media y varianza, la función de distribución acumulativa de la distribución uniforme continua es:${\displaystyle \mu }$${\displaystyle \sigma ^{2},}$

${\displaystyle F(x)={\begin{cases}0&{\text{for }}x-\mu <-\sigma {\sqrt {3}},\\{\frac {1}{2}}\left({\frac {x-\mu }{\sigma {\sqrt {3}}}}+1\right)&{\text{for }}-\sigma {\sqrt {3}}\leq x-\mu <\sigma {\sqrt {3}},\\1&{\text{for }}x-\mu \geq \sigma {\sqrt {3}};\end{cases}}}$

Su inversa es:

${\displaystyle F^{-1}(p)=\sigma {\sqrt {3}}(2p-1)+\mu \quad {\text{ for }}0\leq p\leq 1.}$

Para una variable aleatoria encuentre${\displaystyle X\sim U(0,23),}$${\displaystyle P(2<X<18):}$

${\displaystyle P(2<X<18)=(18-2)\cdot {\frac {1}{23-0}}={\frac {16}{23}}.}$

En una representación gráfica de la función de distribución uniforme continua , el área bajo la curva dentro de los límites especificados, que muestra la probabilidad, es un rectángulo. Para el ejemplo específico anterior, la base sería ⁠ ⁠ y la altura sería ⁠ ⁠ ^[5]${\displaystyle [f(x){\text{ vs }}x],}$${\displaystyle 16,}$${\displaystyle {\tfrac {1}{23}}.}$

Para una variable aleatoria encuentre${\displaystyle X\sim U(0,23),}$${\displaystyle P(X>12\ |\ X>8):}$

${\displaystyle P(X>12\ |\ X>8)=(23-12)\cdot {\frac {1}{23-8}}={\frac {11}{15}}.}$

El ejemplo anterior es un caso de probabilidad condicional para la distribución uniforme continua: dado que ⁠ ⁠${\displaystyle X>8}$ es verdadero, ¿cuál es la probabilidad de que ⁠ ⁠${\displaystyle X>12?}$ La probabilidad condicional cambie el espacio muestral, por lo que se debe calcular una nueva longitud de intervalo ⁠ ⁠${\displaystyle b-a'}$ , donde y ^[5] La representación gráfica seguiría el Ejemplo 1, donde el área bajo la curva dentro de los límites especificados muestra la probabilidad; la base del rectángulo sería ⁠ ⁠ y la altura sería ⁠ ⁠ ^[5]${\displaystyle b=23}$${\displaystyle a'=8.}$${\displaystyle 11,}$${\displaystyle {\tfrac {1}{15}}.}$

La función generadora de momentos de la distribución uniforme continua es: ^[6]

${\displaystyle M_{X}=\mathrm {E} (\mathrm {e} ^{tX})=\int _{a}^{b}\mathrm {e} ^{tx}{\frac {dx}{b-a}}={\frac {\mathrm {e} ^{tb}-\mathrm {e} ^{ta}}{t(b-a)}}={\frac {B^{t}-A^{t}}{t(b-a)}},}$

a partir de los cuales podemos calcular los momentos brutos ${\displaystyle m_{k}:}$

${\displaystyle m_{1}={\frac {a+b}{2}},}$

${\displaystyle m_{2}={\frac {a^{2}+ab+b^{2}}{3}},}$

${\displaystyle m_{k}={\frac {\sum _{i=0}^{k}a^{i}b^{k-i}}{k+1}}.}$

Para una variable aleatoria que sigue una distribución uniforme continua, el valor esperado es y la varianza es${\displaystyle m_{1}={\tfrac {a+b}{2}},}$${\displaystyle m_{2}-m_{1}^{2}={\tfrac {(b-a)^{2}}{12}}.}$

Para el caso especial, la función de densidad de probabilidad de la distribución uniforme continua es:${\displaystyle a=-b,}$

${\displaystyle f(x)={\begin{cases}{\frac {1}{2b}}&{\text{for }}-b\leq x\leq b,\\[8pt]0&{\text{otherwise}};\end{cases}}}$

La función generadora de momentos se reduce a la forma simple:

${\displaystyle M_{X}={\frac {\sinh bt}{bt}}.}$

Para el -ésimo cumulante${\displaystyle n\geq 2,}$ de la distribución uniforme continua en el intervalo es donde es el -ésimo número de Bernoulli . [ ⁷ ]${\displaystyle n}$${\displaystyle [-{\tfrac {1}{2}},{\tfrac {1}{2}}]}$${\displaystyle {\tfrac {B_{n}}{n}},}$${\displaystyle B_{n}}$${\displaystyle n}$

La distribución uniforme continua con parámetros e ie se denomina distribución uniforme estándar .${\displaystyle a=0}$${\displaystyle b=1,}$${\displaystyle U(0,1),}$

Una propiedad interesante de la distribución uniforme estándar es que si tiene una distribución uniforme estándar, entonces también la tiene Esta propiedad se puede utilizar para generar variables antitéticas , entre otras cosas. En otras palabras, esta propiedad se conoce como el método de inversión donde la distribución uniforme estándar continua se puede utilizar para generar números aleatorios para cualquier otra distribución continua. ^[4] Si es un número aleatorio uniforme con distribución uniforme estándar, es decir con entonces genera un número aleatorio de cualquier distribución continua con la función de distribución acumulativa especificada ^[4]${\displaystyle u_{1}}$${\displaystyle 1-u_{1}.}$${\displaystyle u_{1}}$${\displaystyle U(0,1),}$${\displaystyle x=F^{-1}(u_{1})}$${\displaystyle x}$ ${\displaystyle F.}$

Siempre que se sigan las mismas convenciones en los puntos de transición, la función de densidad de probabilidad de la distribución uniforme continua también puede expresarse en términos de la función de escalón de Heaviside como:

${\displaystyle f(x)={\frac {\operatorname {H} (x-a)-\operatorname {H} (x-b)}{b-a}},}$

o en términos de la función rectángulo como:

${\displaystyle f(x)={\frac {1}{b-a}}\ \operatorname {rect} \left({\frac {x-{\frac {a+b}{2}}}{b-a}}\right).}$

No existe ninguna ambigüedad en el punto de transición de la función de signo . Utilizando la convención de máximo medio en los puntos de transición, la distribución uniforme continua puede expresarse en términos de la función de signo como:

${\displaystyle f(x)={\frac {\operatorname {sgn} {(x-a)}-\operatorname {sgn} {(x-b)}}{2(b-a)}}.}$

La media (primer momento bruto ) de la distribución uniforme continua es:

${\displaystyle E(X)=\int _{a}^{b}x{\frac {dx}{b-a}}={\frac {b^{2}-a^{2}}{2(b-a)}}={\frac {b+a}{2}}.}$

El segundo momento crudo de esta distribución es:

${\displaystyle E(X^{2})=\int _{a}^{b}x^{2}{\frac {dx}{b-a}}={\frac {b^{3}-a^{3}}{3(b-a)}}.}$

En general, el momento bruto -ésimo de esta distribución es:${\displaystyle n}$

${\displaystyle E(X^{n})=\int _{a}^{b}x^{n}{\frac {dx}{b-a}}={\frac {b^{n+1}-a^{n+1}}{(n+1)(b-a)}}.}$

La varianza (segundo momento central ) de esta distribución es:

${\displaystyle V(X)=E\left({\big (}X-E(X){\big )}^{2}\right)=\int _{a}^{b}\left(x-{\frac {a+b}{2}}\right)^{2}{\frac {dx}{b-a}}={\frac {(b-a)^{2}}{12}}.}$

Sea una muestra iid de y sea la estadística de orden -ésimo de esta muestra.${\displaystyle X_{1},...,X_{n}}$${\displaystyle U(0,1),}$${\displaystyle X_{(k)}}$${\displaystyle k}$

${\displaystyle X_{(k)}}$tiene una distribución beta , con parámetros y ⁠ ⁠${\displaystyle k}$${\displaystyle n-k+1.}$

El valor esperado es:

${\displaystyle \operatorname {E} \left(X_{(k)}\right)={k \over n+1}.}$

Este hecho es útil al realizar gráficos Q–Q .

La varianza es:

${\displaystyle \operatorname {V} \left(X_{(k)}\right)={k(n-k+1) \over (n+1)^{2}(n+2)}.}$

La probabilidad de que una variable aleatoria distribuida de manera uniforme y continua caiga dentro de cualquier intervalo de longitud fija es independiente de la ubicación del intervalo en sí (pero depende del tamaño del intervalo ), siempre que el intervalo esté contenido en el soporte de la distribución.${\displaystyle (\ell )}$

De hecho, si y si es un subintervalo de con fijo entonces:${\displaystyle X\sim U(a,b)}$${\displaystyle [x,x+\ell ]}$${\displaystyle [a,b]}$${\displaystyle \ell >0,}$

${\displaystyle P{\big (}X\in [x,x+\ell ]{\big )}=\int _{x}^{x+\ell }{\frac {dy}{b-a}}={\frac {\ell }{b-a}},}$

lo cual es independiente de Este hecho motiva el nombre de la distribución.${\displaystyle x.}$

La distribución uniforme puede generalizarse a conjuntos más generales que los intervalos.

Formalmente, sea un conjunto de Borel de medida de Lebesgue finita y positiva, es decir, La distribución uniforme en se puede especificar definiendo la función de densidad de probabilidad como cero fuera y constantemente igual a en${\displaystyle S}$ ${\displaystyle \lambda (S),}$${\displaystyle 0<\lambda (S)<+\infty .}$${\displaystyle S}$${\displaystyle S}$${\displaystyle {\tfrac {1}{\lambda (S)}}}$${\displaystyle S.}$

Un caso especial interesante es cuando el conjunto S es un símplex . Es posible obtener una distribución uniforme en el símplex estándar de n vértices de la siguiente manera. ^{[8] : Teoría 4.1.} Tome n variables aleatorias independientes con la misma distribución exponencial ; denotelas por X ₁ ,...,X _n ; y sea Y _i  := X _i / (suma _i X _i ). Entonces, el vector Y ₁ ,...,Y _n está distribuido uniformemente en el símplex.

• Si X tiene una distribución uniforme estándar, entonces, mediante el método de muestreo por transformada inversa , Y = − λ ⁻¹ ln( X ) tiene una distribución exponencial con parámetro (de tasa) λ .
• Si X tiene una distribución uniforme estándar, entonces Y = X ⁿ tiene una distribución beta con parámetros (1/ n ,1). Por lo tanto,
• La distribución de Irwin-Hall es la suma de n distribuciones i.id U (0,1).
• La distribución de Bates es el promedio de n distribuciones i.id U (0,1).
• La distribución uniforme estándar es un caso especial de la distribución beta , con parámetros (1,1).
• La suma de dos distribuciones uniformes independientes U ₁ (a,b)+ U ₂ (c,d) produce una distribución trapezoidal , simétrica respecto de su media, sobre el soporte [a+c,b+d]. La meseta tiene un ancho igual a la diferencia absoluta del ancho de U ₁ y U ₂ . El ancho de las partes inclinadas corresponde al ancho de la distribución uniforme más estrecha.
  • Si las distribuciones uniformes tienen el mismo ancho w, el resultado es una distribución triangular , simétrica respecto de su media, sobre el soporte [a+c,a+c+2w].
  • La suma de dos distribuciones independientes, uniformes e igualmente distribuidas U ₁ (a,b)+ U _{2 (a,b) produce una} distribución triangular simétrica en el soporte [2a,2b].
• La distancia entre dos variables aleatorias uniformes iid | U ₁ (a,b)- U ₂ (a,b)| también tiene una distribución triangular , aunque no simétrica, en el soporte [0,ba].

Dada una distribución uniforme con valores desconocidos, el estimador insesgado de varianza mínima (UMVUE) para el máximo es:${\displaystyle [0,b]}$${\displaystyle b,}$

${\displaystyle {\hat {b}}_{\text{UMVU}}={\frac {k+1}{k}}m=m+{\frac {m}{k}},}$

donde es el máximo de la muestra y es el tamaño de la muestra , muestreo sin reemplazo (aunque esta distinción casi seguramente no hace ninguna diferencia para una distribución continua). Esto se deduce por las mismas razones que la estimación para la distribución discreta , y puede verse como un caso muy simple de estimación de espaciado máximo . Este problema se conoce comúnmente como el problema del tanque alemán , debido a la aplicación de la estimación máxima a las estimaciones de la producción de tanques alemanes durante la Segunda Guerra Mundial .${\displaystyle m}$${\displaystyle k}$

El método del estimador de momentos es:

${\displaystyle {\hat {b}}_{MM}=2{\bar {X}},}$

¿Dónde está la media de la muestra?${\displaystyle {\bar {X}}}$

El estimador de máxima verosimilitud es:

${\displaystyle {\hat {b}}_{ML}=m,}$

donde es el máximo de la muestra , también denotado como la estadística de orden máximo de la muestra.${\displaystyle m}$${\displaystyle m=X_{(n)},}$

Dada una distribución uniforme en con a desconocida , el estimador de máxima verosimilitud para a es:${\displaystyle [a,b]}$

${\displaystyle {\hat {a}}_{ML}=\min\{X_{1},\dots ,X_{n}\}}$,

el mínimo de la muestra . ^[9]

El punto medio de la distribución es tanto la media como la mediana de la distribución uniforme. Aunque tanto la media muestral como la mediana muestral son estimadores insesgados del punto medio, ninguno es tan eficiente como el rango medio muestral , es decir, la media aritmética del máximo y el mínimo muestral, que es el estimador UMVU del punto medio (y también la estimación de máxima verosimilitud ).${\displaystyle {\tfrac {a+b}{2}},}$

Sea una muestra de donde es el valor máximo en la población. Entonces tiene la densidad de Lebesgue-Borel ^[10]${\displaystyle X_{1},X_{2},X_{3},...,X_{n}}$${\displaystyle U_{[0,L]},}$${\displaystyle L}$${\displaystyle X_{(n)}=\max(X_{1},X_{2},X_{3},...,X_{n})}$${\displaystyle f={\frac {d\Pr _{X_{(n)}}}{d\lambda }}:}$

${\displaystyle f(t)=n{\frac {1}{L}}\left({\frac {t}{L}}\right)^{n-1}\!=n{\frac {t^{n-1}}{L^{n}}}1\!\!1_{[0,L]}(t),}$¿Dónde está la función indicadora de${\displaystyle 1\!\!1_{[0,L]}}$${\displaystyle [0,L].}$

El intervalo de confianza dado anteriormente es matemáticamente incorrecto, ya que

${\displaystyle \Pr {\big (}[{\hat {\theta }},{\hat {\theta }}+\varepsilon ]\ni \theta {\big )}\geq 1-\alpha }$

no se puede resolver sin el conocimiento de . Sin embargo, se puede resolver${\displaystyle \varepsilon }$${\displaystyle \theta }$

${\displaystyle \Pr {\big (}[{\hat {\theta }},{\hat {\theta }}(1+\varepsilon )]\ni \theta {\big )}\geq 1-\alpha }$Para cualquier cosa desconocida pero válida.${\displaystyle \varepsilon \geq (1-\alpha )^{-1/n}-1}$${\displaystyle \theta ;}$

Luego se elige el intervalo más pequeño posible que cumpla la condición anterior. Nótese que la longitud del intervalo depende de la variable aleatoria.${\displaystyle \varepsilon }$${\displaystyle {\hat {\theta }}.}$

Las probabilidades de una función de distribución uniforme son fáciles de calcular debido a la simplicidad de la forma de la función. ^[2] Por lo tanto, existen varias aplicaciones para las que se puede utilizar esta distribución, como se muestra a continuación: situaciones de prueba de hipótesis, casos de muestreo aleatorio, finanzas, etc. Además, generalmente, los experimentos de origen físico siguen una distribución uniforme (por ejemplo, emisión de partículas radiactivas ). ^[1] Sin embargo, es importante señalar que en cualquier aplicación, existe el supuesto inmutable de que la probabilidad de caer en un intervalo de longitud fija es constante. ^[2]

En el campo de la economía, por lo general la demanda y la reposición pueden no seguir la distribución normal esperada. Como resultado, se utilizan otros modelos de distribución para predecir mejor las probabilidades y tendencias, como el proceso de Bernoulli . ^[11] Pero según Wanke (2008), en el caso particular de investigar el tiempo de entrega para la gestión de inventario al comienzo del ciclo de vida cuando se analiza un producto completamente nuevo, la distribución uniforme resulta más útil. ^[11] En esta situación, otra distribución puede no ser viable ya que no hay datos existentes sobre el nuevo producto o que el historial de demanda no está disponible, por lo que realmente no hay una distribución apropiada o conocida. ^[11] La distribución uniforme sería ideal en esta situación ya que la variable aleatoria del tiempo de entrega (relacionada con la demanda) es desconocida para el nuevo producto, pero es probable que los resultados oscilen entre un rango plausible de dos valores. ^[11] El tiempo de entrega representaría así la variable aleatoria. A partir del modelo de distribución uniforme, se pudieron calcular otros factores relacionados con el tiempo de entrega, como el nivel de servicio del ciclo y la escasez por ciclo. También se observó que también se utilizó la distribución uniforme debido a la simplicidad de los cálculos. ^[11]

La distribución uniforme es útil para el muestreo a partir de distribuciones arbitrarias. Un método general es el método de muestreo por transformada inversa, que utiliza la función de distribución acumulativa (CDF) de la variable aleatoria objetivo. Este método es muy útil en el trabajo teórico. Dado que las simulaciones que utilizan este método requieren invertir la CDF de la variable objetivo, se han ideado métodos alternativos para los casos en los que la CDF no se conoce en forma cerrada. Uno de estos métodos es el muestreo por rechazo .

La distribución normal es un ejemplo importante en el que el método de transformación inversa no es eficiente. Sin embargo, existe un método exacto, la transformación de Box-Muller , que utiliza la transformación inversa para convertir dos variables aleatorias uniformes independientes en dos variables aleatorias independientes distribuidas normalmente .

En la conversión de analógico a digital, se produce un error de cuantificación. Este error se debe a un redondeo o a un truncamiento. Cuando la señal original es mucho mayor que un bit menos significativo (LSB) , el error de cuantificación no está significativamente correlacionado con la señal y tiene una distribución aproximadamente uniforme. Por lo tanto, el error RMS se deriva de la varianza de esta distribución.

Existen muchas aplicaciones en las que resulta útil realizar experimentos de simulación. Muchos lenguajes de programación cuentan con implementaciones para generar números pseudoaleatorios que se distribuyen de manera efectiva de acuerdo con la distribución uniforme estándar.

Por otro lado, los números distribuidos uniformemente se utilizan a menudo como base para la generación de variables aleatorias no uniformes .

Si es un valor muestreado de la distribución uniforme estándar, entonces el valor sigue la distribución uniforme parametrizada por y como se describió anteriormente.${\displaystyle u}$${\displaystyle a+(b-a)u}$${\displaystyle a}$${\displaystyle b,}$

Si bien los orígenes históricos de la concepción de la distribución uniforme no son concluyentes, se especula que el término "uniforme" surgió del concepto de equiprobabilidad en los juegos de dados (nótese que los juegos de dados tendrían un espacio muestral uniforme discreto y no continuo). La equiprobabilidad fue mencionada en el Liber de Ludo Aleae de Gerolamo Cardano , un manual escrito en el siglo XVI y detallado sobre el cálculo de probabilidad avanzado en relación con los dados. ^[12]

• Distribución uniforme discreta
• Distribución beta
• Transformada de Box-Muller
• Diagrama de probabilidad
• Diagrama Q-Q
• Función rectangular
• Distribución de Irwin-Hall : en el caso degenerado donde n=1, la distribución de Irwin-Hall genera una distribución uniforme entre 0 y 1.
• Distribución de Bates : similar a la distribución de Irwin-Hall, pero reescalada para n. Al igual que la distribución de Irwin-Hall, en el caso degenerado donde n=1, la distribución de Bates genera una distribución uniforme entre 0 y 1.

• Casella, George; Roger L. Berger (2001), Inferencia estadística (2.ª ed.), Thomson Learning, ISBN 978-0-534-24312-8, C.L.C.N.  2001025794

• Calculadora en línea de distribución uniforme (continua)