Tetraedro

En geometría , un tetraedro ( pl.: tetraedros o tetraedros ) , también conocido como pirámide triangular , es un poliedro compuesto por cuatro caras triangulares , seis aristas rectas y cuatro vértices . El tetraedro es el más simple de todos los poliedros convexos ordinarios . ^[1]

El tetraedro es el caso tridimensional del concepto más general de símplex euclidiano y, por lo tanto, también puede llamarse 3-símplex .

El tetraedro es un tipo de pirámide , que es un poliedro con una base poligonal plana y caras triangulares que conectan la base con un punto común. En el caso del tetraedro, la base es un triángulo (cualquiera de las cuatro caras puede considerarse la base), por lo que el tetraedro también se conoce como "pirámide triangular".

Como todos los poliedros convexos , un tetraedro se puede plegar a partir de una sola hoja de papel. Tiene dos redes de este tipo . ^[1]

Para cualquier tetraedro existe una esfera (llamada circunsfera ) en la que se encuentran los cuatro vértices, y otra esfera (la insfera ) tangente a las caras del tetraedro. ^[2]

Un tetraedro regular es un tetraedro en el que las cuatro caras son triángulos equiláteros . En otras palabras, todas sus caras tienen el mismo tamaño y forma (son congruentes) y todas las aristas tienen la misma longitud. Un poliedro convexo en el que todas sus caras son triángulos equiláteros es el deltaedro . Hay ocho deltaedros convexos, uno de los cuales es el tetraedro regular. ^[3]

El tetraedro regular es también uno de los cinco sólidos platónicos regulares , un conjunto de poliedros en el que todas sus caras son polígonos regulares . ^[4] Conocido desde la antigüedad, el sólido platónico recibe su nombre del filósofo griego Platón , quien asoció esos cuatro sólidos con la naturaleza. El tetraedro regular fue considerado como el elemento clásico del fuego , debido a su interpretación de que su esquina más aguda era la más penetrante. ^[5]

El tetraedro regular es autodual, es decir, su dual es otro tetraedro regular. La figura compuesta que comprende dos tetraedros duales de este tipo forma un octaedro estrellado o stella octangula . Su interior es un octaedro y, en consecuencia, un octaedro regular es el resultado de cortar, de un tetraedro regular, cuatro tetraedros regulares de la mitad del tamaño lineal (es decir, rectificar el tetraedro).

El tetraedro está relacionado con otros dos sólidos: por truncamiento, el tetraedro se convierte en un tetraedro truncado . El dual de este sólido es el triakistetraedro , un tetraedro regular con cuatro pirámides triangulares unidas a cada una de sus caras, es decir, su kleetopo .

Los tetraedros regulares por sí solos no se teselan (llenan el espacio), pero si se alternan con octaedros regulares en la proporción de dos tetraedros por octaedro, forman el panal cúbico alternado , que es una teselación. Algunos tetraedros que no son regulares, incluidos el ortosquema de Schläfli y el tetraedro de Hill , pueden teselarse.

Dado que el tetraedro regular con longitud de arista . El área de superficie de un tetraedro regular es cuatro veces el área de un triángulo equilátero: ^[6] La altura de un tetraedro regular es . ^[7] El volumen de un tetraedro regular se puede determinar de manera similar a las otras pirámides, un tercio de la base y su altura. Como la base es equilátera, es: ^[6] Su volumen también se puede obtener diseccionando un cubo en tres partes. ^[8]${\estilo de visualización a}$${\estilo de visualización A}$$${\displaystyle A=4\cdot \left({\frac {\sqrt {3}}{4}}a^{2}\right)=a^{2}{\sqrt {3}}\approx 1.732a^{2}.}$$${\textstyle {\frac {\sqrt {6}}{3}}a}$$${\displaystyle V={\frac {1}{3}}\cdot \left({\frac {\sqrt {3}}{4}}a^{2}\right)\cdot {\frac {\sqrt {6}}{3}}a={\frac {a^{3}}{6{\sqrt {2}}}}\approx 0,118a^{3}.}$$

Su ángulo diedro —el ángulo entre dos planos— y su ángulo entre líneas desde el centro de un tetraedro regular entre dos vértices ^[a] son ​​respectivamente: ^[9]$${\displaystyle {\begin{aligned}\arccos \left({\frac {1}{3}}\right)&=\arctan \left(2{\sqrt {2}}\right)\aproximadamente 70,529^{\circ },\\\arccos \left(-{\frac {1}{3}}\right)&=2\arctan \left({\sqrt {2}}\right)\aproximadamente 109,471^{\circ }.\end{aligned}}}$$

Los radios de su circunsfera , insfera , mediasfera y exsfera son: ^[6] Para un tetraedro regular con longitud de lado , el radio de su esfera circunscrita y distancias desde un punto arbitrario en el espacio tridimensional hasta sus cuatro vértices, es: ^[10]${\estilo de visualización R}$ ${\estilo de visualización r}$ ${\ Displaystyle r _ {\ mathrm {M}}}$ ${\ Displaystyle r _ {\ mathrm {E}}}$$${\displaystyle {\begin{aligned}R={\frac {\sqrt {6}}{4}}a,&\qquad r={\frac {1}{3}}R={\frac {a}{\sqrt {24}}},\\r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}},&\qquad r_{\mathrm {E} }={\frac {a}{\sqrt {6}}}.\end{aligned}}}$$${\estilo de visualización a}$${\estilo de visualización R}$$estilo de visualización d_{i}}$$${\displaystyle {\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\derecha)^{2},\\4\izquierda(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\derecha)&=\izquierda(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\derecha)^{2}.\end{alineado}}}$$

Respecto del plano base la pendiente de una cara (2 √ 2 ) es el doble de la de una arista ( √ 2 ), lo que corresponde al hecho de que la distancia horizontal recorrida desde la base hasta el vértice a lo largo de una arista es el doble de la que recorre la mediana de una cara. En otras palabras, si C es el baricentro de la base, la distancia de C a un vértice de la base es el doble de la que hay desde C al punto medio de una arista de la base. Esto se deduce del hecho de que las medianas de un triángulo se cortan en su baricentro, y este punto divide cada una de ellas en dos segmentos, uno de los cuales es el doble de largo que el otro (ver demostración ).

Su ángulo sólido en un vértice subtendido por una cara es Esto es aproximadamente 0,55129 estereorradianes , 1809,8 grados cuadrados o 0,04387 spats .$${\displaystyle {\begin{aligned}\arccos \left({\frac {23}{27}}\right)&={\frac {\pi }{2}}-3\arcsin \left({\frac {1}{3}}\right)\\&=3\arccos \left({\frac {1}{3}}\right)-\pi \end{aligned}}}$$

Una forma de construir un tetraedro regular es utilizando las siguientes coordenadas cartesianas , que definen los cuatro vértices de un tetraedro con longitud de arista 2, centrado en el origen y aristas de dos niveles:$${\displaystyle \left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{y}}\quad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)}$$

Expresado simétricamente como 4 puntos sobre la esfera unitaria , centroide en el origen, con la cara inferior paralela al plano, los vértices son: con longitud de arista de .${\estilo de visualización xy}$$${\displaystyle {\begin{aligned}\left({\sqrt {\frac {8}{9}}},0,-{\frac {1}{3}}\right),&\quad \left(-{\sqrt {\frac {2}{9}}},{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right),\\\left(-{\sqrt {\frac {2}{9}}},-{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right),&\quad (0,0,1)\end{aligned}}}$$${\textstyle {\frac {2{\sqrt {6}}}{3}}}$

Un tetraedro regular se puede incrustar dentro de un cubo de dos maneras, de modo que cada vértice sea un vértice del cubo y cada arista sea una diagonal de una de las caras del cubo. Para una de esas incrustaciones, las coordenadas cartesianas de los vértices son Esto produce un tetraedro con una longitud de arista , centrado en el origen. Para el otro tetraedro (que es dual del primero), invierta todos los signos. Los vértices de estos dos tetraedros combinados son los vértices de un cubo, lo que demuestra que el tetraedro regular es el semicubo 3- , un poliedro que se forma alternando un cubo. Esta forma tiene un diagrama de Coxeter$${\displaystyle {\begin{aligned}(1,1,1),&\quad (1,-1,-1),\\(-1,1,-1),&\quad (-1,-1,1).\end{aligned}}}$$${\displaystyle 2{\sqrt {2}}}$ y el símbolo de Schläfli .${\displaystyle \mathrm {h} \{4,3\}}$

Los vértices de un cubo se pueden agrupar en dos grupos de cuatro, cada uno de los cuales forma un tetraedro regular, mostrando uno de los dos tetraedros del cubo. Las simetrías de un tetraedro regular corresponden a la mitad de las de un cubo: las que asignan los tetraedros a sí mismos, y no entre sí. El tetraedro es el único sólido platónico que no se asigna a sí mismo por inversión de puntos .

El tetraedro regular tiene 24 isometrías, formando el grupo de simetría conocido como simetría tetraédrica completa . Este grupo de simetría es isomorfo al grupo simétrico . Se pueden clasificar de la siguiente manera:${\displaystyle \mathrm {T} _{\mathrm {d} }}$ ${\displaystyle S_{4}}$

• Tiene simetría tetraédrica rotacional . Esta simetría es isomorfa al grupo alternante —la identidad y 11 rotaciones propias— con las siguientes clases de conjugación (entre paréntesis se dan las permutaciones de los vértices, o correspondientemente, las caras, y la representación del cuaternión unitario ):${\displaystyle \mathrm {T} }$ ${\displaystyle A_{4}}$
  • identidad (identidad; 1)
  • rotación alrededor de un eje que pasa por un vértice, perpendicular al plano opuesto, en un ángulo de ±120°: 4 ejes, 2 por eje, juntos 8 ((1 2 3) , etc .;1 ± i ± j ± k/2⁠ )
  • rotación en un ángulo de 180° de manera que un borde se corresponde con el borde opuesto: 3 ((1 2)(3 4) , etc.; i , j , k )
• reflexiones en un plano perpendicular a un borde: 6
• reflexiones en un plano combinadas con una rotación de 90° alrededor de un eje perpendicular al plano: 3 ejes, 2 por eje, en total 6; equivalentemente, son rotaciones de 90° combinadas con inversión ( x se asigna a − x ): las rotaciones corresponden a las del cubo sobre ejes cara a cara

El tetraedro regular tiene dos proyecciones ortogonales especiales , una centrada en un vértice o equivalentemente en una cara, y otra centrada en una arista. La primera corresponde al plano A ₂ de Coxeter .

Proyección ortográfica

Centrado por	Cara/vértice	Borde
Imagen
Simetría proyectiva	[3]	[4]

Los dos bordes opuestos perpendiculares y oblicuos de un tetraedro regular definen un conjunto de planos paralelos. Cuando uno de estos planos interseca el tetraedro, la sección transversal resultante es un rectángulo . ^[11] Cuando el plano de intersección está cerca de uno de los bordes, el rectángulo es largo y delgado. Cuando está a mitad de camino entre los dos bordes, la intersección es un cuadrado . La relación de aspecto del rectángulo se invierte al pasar este punto medio. Para la intersección del cuadrado en el punto medio, la línea límite resultante atraviesa cada cara del tetraedro de manera similar. Si el tetraedro se divide en dos en este plano, ambas mitades se convierten en cuñas .

Esta propiedad también se aplica a los difenoides tetragonales cuando se aplica a los dos pares de aristas especiales.

El tetraedro también puede representarse como un mosaico esférico (de triángulos esféricos ) y proyectarse sobre el plano mediante una proyección estereográfica . Esta proyección es conforme y conserva los ángulos, pero no las áreas ni las longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Proyección ortográfica	Proyección estereográfica

Los tetraedros regulares se pueden apilar cara a cara en una cadena aperiódica quiral llamada hélice de Boerdijk-Coxeter .

En cuatro dimensiones , todos los 4-politopos regulares convexos con celdas tetraédricas (de 5 , 16 y 600 celdas ) se pueden construir como teselas de la 3-esfera mediante estas cadenas, que se vuelven periódicas en el espacio tridimensional de la superficie límite del 4-politopo.

Relaciones de subgrupos de simetría tetraédrica

Simetrías tetraédricas mostradas en diagramas tetraédricos

Los tetraedros que no tienen cuatro caras equiláteras se clasifican y nombran por las simetrías que poseen.

Si los tres pares de aristas opuestas de un tetraedro son perpendiculares , se denomina tetraedro ortocéntrico . Cuando solo un par de aristas opuestas son perpendiculares, se denomina tetraedro semiortocéntrico . En un tetraedro trirectangular, los tres ángulos de las caras en un vértice son ángulos rectos , como en la esquina de un cubo.

Un tetraedro isodinámico es aquel en el que las cevianas que unen los vértices a los incentros de las caras opuestas son concurrentes .

Un tetraedro isogónico tiene cevianas concurrentes que unen los vértices a los puntos de contacto de las caras opuestas con la esfera inscrita del tetraedro.

Un disfenoide es un tetraedro con cuatro triángulos congruentes como caras; los triángulos necesariamente tienen todos los ángulos agudos. El tetraedro regular es un caso especial de un disfenoide. Otros nombres para la misma forma incluyen bisfenoide, tetraedro isósceles y tetraedro equifacial.

Un 3-ortosquema es un tetraedro en el que las cuatro caras son triángulos rectángulos . Un 3-ortosquema no es un disfenoide, porque sus aristas opuestas no tienen la misma longitud. No es posible construir un disfenoide con caras de triángulos rectángulos o triángulos obtusos.

Un ortosquema es un símplex irregular que es la envoltura convexa de un árbol en el que todos los bordes son mutuamente perpendiculares. En un ortosquema tridimensional, el árbol consta de tres bordes perpendiculares que conectan los cuatro vértices en una trayectoria lineal que realiza dos giros en ángulo recto. El 3-ortosquema es un tetraedro que tiene dos ángulos rectos en cada uno de dos vértices, por lo que otro nombre para él es tetraedro birrectangular . También se le llama tetraedro cuadrirrectangular porque contiene cuatro ángulos rectos. ^[12]

Coxeter también llama a los tetraedros cuadrirrectangulares "tetraedros característicos", debido a su relación integral con los politopos regulares y sus grupos de simetría. ^[13] Por ejemplo, el caso especial de un 3-ortosquema con aristas perpendiculares de igual longitud es característico del cubo , lo que significa que el cubo se puede subdividir en instancias de este ortosquema. Si sus tres aristas perpendiculares son de longitud unitaria, sus aristas restantes son dos de longitud √ 2 y una de longitud √ 3 , por lo que todas sus aristas son aristas o diagonales del cubo. El cubose puede diseccionar en seis de estos 3-ortoesquemasde cuatro maneras diferentes, y las seis rodean la misma diagonal del cubo de √ 3. El cubo también se puede diseccionar en 48 instancias más pequeñas de este mismo 3-ortosquema característico (de una sola manera, mediante todos sus planos de simetría a la vez). El tetraedro característico del cubo es un ejemplo de tetraedro heroniano .

Todo politopo regular, incluido el tetraedro regular, tiene su ortosquema característico . Existe un 3-ortosquema, que es el "tetraedro característico del tetraedro regular". El tetraedro regularse subdivide en 24 instancias de su tetraedro característicopor sus planos de simetría. Los 24 tetraedros característicos del tetraedro regular se presentan en dos formas de imagen especular, 12 de cada una.

Características del tetraedro regular [14]
	borde	arco		diedro
𝒍	${\displaystyle 2}$	109°28′16″	${\displaystyle \pi -2{\text{𝜿}}}$	70°31′44″	${\displaystyle \pi -2{\text{𝟁}}}$
𝟀	${\displaystyle {\sqrt {\tfrac {4}{3}}}\approx 1.155}$	70°31′44″	${\displaystyle 2{\text{𝜿}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝝉 [b]	${\displaystyle 1}$	54°44′8″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜿}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝟁	${\displaystyle {\sqrt {\tfrac {1}{3}}}\approx 0.577}$	54°44′8″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜿}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
${\displaystyle _{0}R/l}$	${\displaystyle {\sqrt {\tfrac {3}{2}}}\approx 1.225}$
${\displaystyle _{1}R/l}$	${\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}$
${\displaystyle _{2}R/l}$	${\displaystyle {\sqrt {\tfrac {1}{6}}}\approx 0.408}$
${\displaystyle {\text{𝜿}}}$		35°15′52″	${\displaystyle {\tfrac {{\text{arc sec }}3}{2}}}$

Si el tetraedro regular tiene una longitud de arista 𝒍 = 2, las seis aristas de su tetraedro característico tienen longitudes , , alrededor de su cara exterior de triángulo rectángulo (las aristas opuestas a los ángulos característicos 𝟀, 𝝉, 𝟁), ^[b] más , , (aristas que son los radios característicos del tetraedro regular). La ruta de 3 aristas a lo largo de las aristas ortogonales del ortosquema es , , , primero desde un vértice de tetraedro hasta un centro de arista de tetraedro, luego girando 90° hasta el centro de una cara de tetraedro, luego girando 90° hasta el centro del tetraedro. El ortosquema tiene cuatro caras de triángulos rectángulos diferentes. La cara exterior es un triángulo 60-90-30 que es un sexto de una cara de tetraedro. Las tres caras interiores del tetraedro son: un triángulo rectángulo con aristas , , , un triángulo rectángulo con aristas , , , y un triángulo rectángulo con aristas , , .${\displaystyle {\sqrt {\tfrac {4}{3}}}}$${\displaystyle 1}$${\displaystyle {\sqrt {\tfrac {1}{3}}}}$${\displaystyle {\sqrt {\tfrac {3}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$${\displaystyle 1}$${\displaystyle {\sqrt {\tfrac {1}{3}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$${\displaystyle 1}$${\displaystyle {\sqrt {\tfrac {3}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{3}}}}$${\displaystyle {\sqrt {\tfrac {1}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$${\displaystyle {\sqrt {\tfrac {4}{3}}}}$${\displaystyle {\sqrt {\tfrac {3}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$

Un tetraedro que llena el espacio se empaqueta con copias directamente congruentes o enantiomorfas ( imagen especular ) de sí mismo para formar un espacio de mosaicos. ^[15] El cubo se puede diseccionar en seis 3-ortosquemas, tres levógiros y tres diestros (uno de cada uno en cada cara del cubo), y los cubos pueden llenar el espacio, por lo que el 3-ortosquema característico del cubo es un tetraedro que llena el espacio en este sentido. (El ortosquema característico del cubo es uno de los tetraedros de Hill , una familia de tetraedros que llenan el espacio. Todos los tetraedros que llenan el espacio son congruentes en tijera con un cubo).

Un difenoide puede ser un tetraedro que llena el espacio en el sentido directamente congruente, como en el caso del panal tetraédrico difenoide . Sin embargo, los tetraedros regulares no pueden llenar el espacio por sí mismos (además, no son congruentes en tijera con ningún otro poliedro que pueda llenar el espacio, véase el tercer problema de Hilbert ). El panal tetraédrico-octaédrico llena el espacio con celdas tetraédricas regulares y celdas octaédricas regulares alternadas en una proporción de 2:1.

Un tetraedro irregular, que es el dominio fundamental ^[16] de un grupo de simetría , es un ejemplo de tetraedro de Goursat . Los tetraedros de Goursat generan todos los poliedros regulares (y muchos otros poliedros uniformes) mediante reflexiones especulares, un proceso conocido como construcción caleidoscópica de Wythoff .

En el caso de los poliedros, la construcción de Wythoff dispone tres espejos en ángulos entre sí, como en un caleidoscopio . A diferencia de un caleidoscopio cilíndrico, los espejos de Wythoff están ubicados en tres caras de un tetraedro de Goursat, de modo que los tres espejos se intersecan en un único punto. (El diagrama de Coxeter-Dynkin del poliedro generado contiene tres nodos que representan los tres espejos. El ángulo diedro entre cada par de espejos está codificado en el diagrama, así como la ubicación de un único punto generador que se multiplica por los reflejos del espejo en los vértices del poliedro).

Entre los tetraedros de Goursat que generan panales tridimensionales podemos reconocer un ortosquema (el tetraedro característico del cubo), un ortosquema doble (el tetraedro característico del cubo unido por una cara a su imagen especular) y el difenoide que llena el espacio ilustrado arriba. ^[13] El difenoide es el ortosquema doble unido por una cara a su imagen especular (un ortosquema cuádruple). Por lo tanto, estos tres tetraedros de Goursat, y todos los poliedros que generan por reflexiones, pueden diseccionarse en tetraedros característicos del cubo .

Las isometrías de un tetraedro irregular (sin marcar) dependen de la geometría del tetraedro, con 7 casos posibles. En cada caso se forma un grupo de puntos tridimensional . Pueden existir otras dos isometrías (C ₃ , [3] ⁺ ), y (S ₄ , [2 ⁺ ,4 ⁺ ]) si se incluyen las marcas de las caras o aristas. A continuación se incluyen diagramas tetraédricos para cada tipo, con aristas coloreadas según la equivalencia isométrica y en color gris para aristas únicas.

Nombre del tetraedro				Diagrama de equivalencia de aristas	Descripción
Simetría
Hermoso.	Timonel.	Orbe.	Ordenanza.
Tetraedro regular					Cuatro triángulos equiláteros Forma el grupo de simetría T d , isomorfo al grupo simétrico S 4 . Un tetraedro regular tiene diagrama de Coxeter y el símbolo de Schläfli {3,3}.
T y T	[3,3] [3,3] +	*332 332	24 12
Pirámide triangular					Una base de triángulo equilátero y tres lados de triángulo isósceles iguales Da 6 isometrías, correspondientes a las 6 isometrías de la base. Como permutaciones de los vértices, estas 6 isometrías son la identidad 1, (123), (132), (12), (13) y (23), formando el grupo de simetría C 3v , isomorfo al grupo simétrico , S 3 . Una pirámide triangular tiene símbolo de Schläfli {3}∨( ).
C 3v C 3	[3] [3] +	*33 33	6 3
Esfenoides reflejado		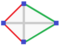			Dos triángulos escalenos iguales con una arista de base común Este tiene dos pares de aristas iguales (1,3), (1,4) y (2,3), (2,4) y por lo demás ninguna arista igual. Las únicas dos isometrías son 1 y la reflexión (34), dando el grupo C s , también isomorfo al grupo cíclico , Z 2 .
Cs = C1h = C1v​​​	[ ]	*	2
Tetraedro irregular (sin simetría)					Cuatro triángulos desiguales Su única isometría es la identidad, y el grupo de simetría es el grupo trivial . Un tetraedro irregular tiene el símbolo de Schläfli ( )∨( )∨( )∨( ).
C 1	[ ] +	1	1
Disfenoides (Cuatro triángulos iguales)
Difénoides tetragonal					Cuatro triángulos isósceles iguales Tiene 8 isometrías. Si las aristas (1,2) y (3,4) son de longitud diferente a las otras 4 entonces las 8 isometrías son la identidad 1, las reflexiones (12) y (34), y las rotaciones de 180° (12)(34), (13)(24), (14)(23) y las rotaciones impropias de 90° (1234) y (1432) que forman el grupo de simetría D 2d . Un disfenoide tetragonal tiene diagrama de Coxetery el símbolo de Schläfli s{2,4}.
D 2d S 4	[2 + ,4] [2 + ,4 + ]	2*2 2×	8 4
Disfenoide rómbico					Cuatro triángulos escalenos iguales Tiene 4 isometrías. Las isometrías son 1 y las rotaciones de 180° (12)(34), (13)(24), (14)(23). Este es el cuatrigrupo de Klein V 4 o Z 2 2 , presente como el grupo puntual D 2 . Un disfenoide rómbico tiene diagrama de Coxetery el símbolo de Schläfli sr{2,2}.
D2​	[2,2] +	222	4
Disfenoides generalizados (2 pares de triángulos iguales)
Difenoide digonal					Dos pares de triángulos isósceles iguales Esto da dos aristas opuestas (1,2) y (3,4) que son perpendiculares pero de longitudes diferentes, y entonces las 4 isometrías son 1, las reflexiones (12) y (34) y la rotación de 180° (12)(34). El grupo de simetría es C 2v , isomorfo al cuatrigrupo de Klein V 4 . Un disfenoide digonal tiene el símbolo de Schläfli { }∨{ }.
C2vC2​ ​​	[2] [2] +	*22 22	4 2
Disfenoide fílico					Dos pares de triángulos escalenos o isósceles iguales Este tiene dos pares de aristas iguales (1,3), (2,4) y (1,4), (2,3) pero por lo demás ninguna arista igual. Las únicas dos isometrías son 1 y la rotación (12)(34), lo que da al grupo C 2 isomorfo al grupo cíclico Z 2 .
C 2	[2] +	22	2

La subdivisión de tetraedros es un proceso utilizado en geometría computacional y modelado 3D para dividir un tetraedro en varios tetraedros más pequeños. Este proceso mejora la complejidad y el detalle de las mallas tetraédricas, lo que resulta particularmente beneficioso en simulaciones numéricas, análisis de elementos finitos y gráficos por computadora. Uno de los métodos de subdivisión más utilizados es la bisección del borde más largo (LEB) , que identifica el borde más largo del tetraedro y lo divide en su punto medio, generando dos tetraedros nuevos más pequeños. Cuando este proceso se repite varias veces, bisecando todos los tetraedros generados en cada iteración anterior, el proceso se denomina LEB iterativo.

Una clase de similitud es el conjunto de tetraedros con la misma forma geométrica, independientemente de su posición, orientación y escala específicas. Por lo tanto, dos tetraedros cualesquiera que pertenezcan a la misma clase de similitud pueden transformarse entre sí mediante una transformación afín. El resultado de tener un número limitado de clases de similitud en los métodos de subdivisión iterativos es significativo para el modelado y la simulación computacionales, ya que reduce la variabilidad en las formas y tamaños de los tetraedros generados, lo que evita la formación de elementos altamente irregulares que podrían comprometer los resultados de la simulación.

Se ha demostrado que el LEB iterativo del tetraedro regular produce solo 8 clases de similitud. Además, en el caso de tetraedros casi equiláteros donde sus dos aristas más largas no están conectadas entre sí, y la relación entre su arista más larga y su arista más corta es menor o igual a , el LEB iterado no produce más de 37 clases de similitud. ^[17]${\displaystyle {\sqrt {3/2}}}$

El volumen de un tetraedro se puede obtener de muchas maneras. Se puede obtener utilizando la fórmula del volumen de la pirámide: donde es el área de la base y es la altura desde la base hasta el vértice. Esto se aplica para cada una de las cuatro opciones de la base, por lo que las distancias desde los vértices hasta las caras opuestas son inversamente proporcionales a las áreas de estas caras. Otra forma es diseccionando un prisma triangular en tres partes. ^[18]$${\displaystyle V={\frac {1}{3}}Ah.}$$${\displaystyle A}$${\displaystyle h}$

Dados los vértices de un tetraedro en lo siguiente: El volumen de un tetraedro se puede determinar en términos de un determinante , ^[19] o cualquier otra combinación de pares de vértices que formen un grafo simplemente conexo . Comparando esta fórmula con la utilizada para calcular el volumen de un paralelepípedo , concluimos que el volumen de un tetraedro es igual a ⁠$${\displaystyle {\begin{aligned}\mathbf {a} &=(a_{1},a_{2},a_{3}),\\\mathbf {b} &=(b_{1},b_{2},b_{3}),\\\mathbf {c} &=(c_{1},c_{2},c_{3}),\\\mathbf {d} &=(d_{1},d_{2},d_{3}).\end{aligned}}}$$ ${\textstyle {\frac {1}{6}}\det(\mathbf {a} -\mathbf {d} ,\mathbf {b} -\mathbf {d} ,\mathbf {c} -\mathbf {d} )}$1/6⁠ del volumen de cualquier paralelepípedo que comparte con él tres aristas convergentes.

El valor absoluto del triple producto escalar se puede representar como los siguientes valores absolutos de determinantes:

${\displaystyle 6\cdot V={\begin{Vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{Vmatrix}}}$ o donde se expresan como vectores de fila o columna. ${\displaystyle 6\cdot V={\begin{Vmatrix}\mathbf {a} \\\mathbf {b} \\\mathbf {c} \end{Vmatrix}}}$  ${\displaystyle {\begin{cases}\mathbf {a} =(a_{1},a_{2},a_{3}),\\\mathbf {b} =(b_{1},b_{2},b_{3}),\\\mathbf {c} =(c_{1},c_{2},c_{3}),\end{cases}}}$ 

Por eso

${\displaystyle 36\cdot V^{2}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \end{vmatrix}}}$ dónde ${\displaystyle {\begin{cases}\mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma },\\\mathbf {b} \cdot \mathbf {c} =bc\cos {\alpha },\\\mathbf {a} \cdot \mathbf {c} =ac\cos {\beta }.\end{cases}}}$

donde , , y , lo que da${\displaystyle a={\begin{Vmatrix}\mathbf {a} \end{Vmatrix}}}$${\displaystyle b={\begin{Vmatrix}\mathbf {b} \end{Vmatrix}}}$${\displaystyle c={\begin{Vmatrix}\mathbf {c} \end{Vmatrix}}}$

${\displaystyle V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}},\,}$

donde α , β , γ son los ángulos del plano que se dan en el vértice d . El ángulo α , es el ángulo entre las dos aristas que unen el vértice d con los vértices b y c . El ángulo β , lo es para los vértices a y c , mientras que γ , se define por la posición de los vértices a y b .

Si no requerimos que d = 0 entonces

${\displaystyle 6\cdot V=\left|\det \left({\begin{matrix}a_{1}&b_{1}&c_{1}&d_{1}\\a_{2}&b_{2}&c_{2}&d_{2}\\a_{3}&b_{3}&c_{3}&d_{3}\\1&1&1&1\end{matrix}}\right)\right|\,.}$

Dadas las distancias entre los vértices de un tetraedro, el volumen se puede calcular utilizando el determinante de Cayley-Menger :

${\displaystyle 288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}}$

donde los subíndices i , j ∈ {1, 2, 3, 4} representan los vértices { a , b , c , d } y d _ij es la distancia por pares entre ellos, es decir, la longitud del borde que conecta los dos vértices. Un valor negativo del determinante significa que no se puede construir un tetraedro con las distancias dadas. Esta fórmula, a veces llamada fórmula de Tartaglia , se debe esencialmente al pintor Piero della Francesca en el siglo XV, como un análogo tridimensional de la fórmula de Heron del siglo I para el área de un triángulo. ^[20]

Sean , , y las longitudes de tres aristas que se encuentran en un punto, y , , y las de las aristas opuestas. El volumen del tetraedro es: ^[21] donde La fórmula anterior utiliza seis longitudes de aristas, y la siguiente fórmula utiliza tres longitudes de aristas y tres ángulos. ^[21]${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$${\displaystyle x}$${\displaystyle y}$${\displaystyle z}$${\displaystyle V}$$${\displaystyle V={\frac {\sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}}{12}}}$$$${\displaystyle {\begin{aligned}X&=b^{2}+c^{2}-x^{2},\\Y&=a^{2}+c^{2}-y^{2},\\Z&=a^{2}+b^{2}-z^{2}.\end{aligned}}}$$$${\displaystyle V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}}$$

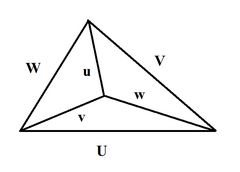
El volumen de un tetraedro se puede determinar utilizando la fórmula de Heron. Supongamos que , , , . , y son las longitudes de las aristas del tetraedro como en la siguiente imagen. Aquí, las primeras tres forman un triángulo, con opuestos , opuestos y opuestos . Entonces, donde y${\displaystyle U}$${\displaystyle V}$${\displaystyle W}$${\displaystyle u}$${\displaystyle v}$${\displaystyle w}$${\displaystyle u}$${\displaystyle U}$${\displaystyle v}$${\displaystyle V}$${\displaystyle w}$${\displaystyle W}$$${\displaystyle V={\frac {\sqrt {\,(-p+q+r+s)\,(p-q+r+s)\,(p+q-r+s)\,(p+q+r-s)}}{192\,u\,v\,w}}}$$$${\displaystyle {\begin{aligned}p={\sqrt {xYZ}},&\quad q={\sqrt {yZX}},\\r={\sqrt {zXY}},&\quad s={\sqrt {xyz}},\end{aligned}}}$$$${\displaystyle {\begin{aligned}X=(w-U+v)(U+v+w),&\quad x=(U-v+w)(v-w+U),\\Y=(u-V+w)(V+w+u),&\quad y=(V-w+u)(w-u+V),\\Z=(v-W+u)(W+u+v),&\quad z=(W-u+v)\,(u-v+W).\end{aligned}}}$$

Cualquier plano que contenga un bimediano (conector de puntos medios de aristas opuestas) de un tetraedro biseca el volumen del tetraedro. ^[22]

En el caso de los tetraedros en el espacio hiperbólico o en la geometría elíptica tridimensional , los ángulos diedros del tetraedro determinan su forma y, por lo tanto, su volumen. En estos casos, el volumen se obtiene mediante la fórmula de Murakami-Yano , elaborada por Jun Murakami y Masakazu Yano. ^[23] Sin embargo, en el espacio euclidiano, al escalar un tetraedro se modifica su volumen, pero no sus ángulos diedros, por lo que no puede existir dicha fórmula.

Dos aristas opuestas cualesquiera de un tetraedro se encuentran sobre dos líneas oblicuas , y la distancia entre las aristas se define como la distancia entre las dos líneas oblicuas. Sea la distancia entre las líneas oblicuas formadas por aristas opuestas y como se calcula aquí . Luego, otra fórmula para el volumen de un tetraedro se da por${\displaystyle d}$${\displaystyle a}$${\displaystyle \mathbf {b} -\mathbf {c} }$${\displaystyle V}$$${\displaystyle V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.}$$

El tetraedro tiene muchas propiedades análogas a las de un triángulo, entre ellas, la insfera, la circunsfera, el tetraedro medial y las exsferas. Tiene centros respectivos, como el incentro, el circuncentro, los excentros, el centro de Spieker y puntos como el baricentro. Sin embargo, generalmente no hay un ortocentro en el sentido de alturas que se intersecan. ^[24]

Gaspard Monge encontró un centro que existe en cada tetraedro, ahora conocido como el punto Monge : el punto donde se intersecan los seis planos medios de un tetraedro. Un plano medio se define como un plano que es ortogonal a una arista que une dos vértices cualesquiera y que también contiene el centroide de una arista opuesta formada al unir los otros dos vértices. Si las alturas del tetraedro se intersecan, entonces el punto Monge y el ortocentro coinciden para dar la clase de tetraedro ortocéntrico .

Una línea ortogonal trazada desde el punto Monge hasta cualquier cara se encuentra con esa cara en el punto medio del segmento de línea entre el ortocentro de esa cara y el pie de la altitud trazada desde el vértice opuesto.

Un segmento de línea que une un vértice de un tetraedro con el centroide de la cara opuesta se llama mediana y un segmento de línea que une los puntos medios de dos aristas opuestas se llama bimediana del tetraedro. Por lo tanto, hay cuatro medianas y tres bimedianas en un tetraedro. Estos siete segmentos de línea son todos concurrentes en un punto llamado centroide del tetraedro. ^[25] Además, las cuatro medianas están divididas en una proporción de 3:1 por el centroide (véase el teorema de Commandino ). El centroide de un tetraedro es el punto medio entre su punto Monge y su circuncentro. Estos puntos definen la línea de Euler del tetraedro que es análoga a la línea de Euler de un triángulo.

El círculo de nueve puntos del triángulo general tiene un análogo en la circunsfera del tetraedro medial de un tetraedro. Es la esfera de doce puntos y, además de los centroides de las cuatro caras del tetraedro de referencia, pasa por cuatro puntos de Euler sustitutos , un tercio del camino desde el punto de Monge hacia cada uno de los cuatro vértices. Finalmente pasa por los cuatro puntos base de las líneas ortogonales trazadas desde cada punto de Euler hasta la cara que no contiene el vértice que generó el punto de Euler. ^[26]

El centro T de la esfera de doce puntos también se encuentra en la línea de Euler. A diferencia de su contraparte triangular, este centro se encuentra a un tercio del camino desde el punto de Monge M hacia el circuncentro. Además, una línea ortogonal que pasa por T hacia una cara elegida es coplanar con otras dos líneas ortogonales hacia la misma cara. La primera es una línea ortogonal que pasa por el punto de Euler correspondiente a la cara elegida. La segunda es una línea ortogonal que pasa por el centroide de la cara elegida. Esta línea ortogonal que pasa por el centro de doce puntos se encuentra a medio camino entre la línea ortogonal del punto de Euler y la línea ortogonal centroidal. Además, para cualquier cara, el centro de doce puntos se encuentra en el punto medio del punto de Euler correspondiente y el ortocentro de esa cara.

El radio de la esfera de doce puntos es un tercio del radio circunscrito del tetraedro de referencia.

Existe una relación entre los ángulos que forman las caras de un tetraedro general dada por ^[27]

${\displaystyle {\begin{vmatrix}-1&\cos {(\alpha _{12})}&\cos {(\alpha _{13})}&\cos {(\alpha _{14})}\\\cos {(\alpha _{12})}&-1&\cos {(\alpha _{23})}&\cos {(\alpha _{24})}\\\cos {(\alpha _{13})}&\cos {(\alpha _{23})}&-1&\cos {(\alpha _{34})}\\\cos {(\alpha _{14})}&\cos {(\alpha _{24})}&\cos {(\alpha _{34})}&-1\\\end{vmatrix}}=0\,}$

donde α _ij es el ángulo entre las caras i y j .

La mediana geométrica de las coordenadas de posición del vértice de un tetraedro y su centro isogónico están asociadas, en circunstancias análogas a las observadas para un triángulo. Lorenz Lindelöf encontró que, correspondiente a cualquier tetraedro dado hay un punto ahora conocido como centro isogónico, O , en el que los ángulos sólidos subtendidos por las caras son iguales, teniendo un valor común de π sr , y en el que los ángulos subtendidos por los bordes opuestos son iguales. ^[28] Un ángulo sólido de π sr es un cuarto del subtendido por todo el espacio. Cuando todos los ángulos sólidos en los vértices de un tetraedro son menores que π sr , O se encuentra dentro del tetraedro, y debido a que la suma de las distancias de O a los vértices es un mínimo, O coincide con la mediana geométrica , M , de los vértices. En el caso de que el ángulo sólido en uno de los vértices, v , mida exactamente π sr, entonces O y M coinciden con v . Sin embargo, si un tetraedro tiene un vértice, v , con un ángulo sólido mayor que π sr, M todavía corresponde a v , pero O se encuentra fuera del tetraedro.

Un tetraedro es un 3- símplex . A diferencia del caso de los otros sólidos platónicos, todos los vértices de un tetraedro regular son equidistantes entre sí (son la única disposición posible de cuatro puntos equidistantes en el espacio tridimensional, por ejemplo en electromagnetismo véase el problema de Thomson ).

La incrustación anterior divide el cubo en cinco tetraedros, uno de los cuales es regular. De hecho, cinco es el número mínimo de tetraedros necesarios para componer un cubo. Para comprobarlo, partiendo de un tetraedro base con 4 vértices, cada tetraedro añadido añade como máximo 1 nuevo vértice, por lo que se deben añadir al menos 4 más para formar un cubo, que tiene 8 vértices.

Inscribir tetraedros dentro del compuesto regular de cinco cubos da dos compuestos regulares más, que contienen cinco y diez tetraedros.

Los tetraedros regulares no pueden teselar el espacio por sí solos, aunque este resultado parece lo suficientemente probable como para que Aristóteles afirmara que era posible. Sin embargo, dos tetraedros regulares pueden combinarse con un octaedro, dando como resultado un romboedro que puede teselar el espacio como el panal tetraédrico-octaédrico .

Por otra parte, se conocen varios tetraedros irregulares, de los cuales se pueden obtener copias que teselan el espacio, por ejemplo, el ortosquema característico del cubo y el difenoides del panal tetraédrico difenoidal . La lista completa sigue siendo un problema abierto. ^[29]

Si se flexibiliza el requisito de que todos los tetraedros tengan la misma forma, se puede teselar el espacio utilizando sólo tetraedros de muchas maneras diferentes. Por ejemplo, se puede dividir un octaedro en cuatro tetraedros idénticos y combinarlos de nuevo con dos tetraedros regulares. (Como nota al margen: estos dos tipos de tetraedros tienen el mismo volumen).

El tetraedro es el único poliedro uniforme que existe porque no tiene caras paralelas.

Un corolario de la ley usual de los senos es que en un tetraedro con vértices O , A , B , C , tenemos

${\displaystyle \sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,}$

Se pueden ver los dos lados de esta identidad como correspondientes a las orientaciones de la superficie en sentido horario y antihorario.

Poniendo cualquiera de los cuatro vértices en el papel de O se obtienen cuatro de esas identidades, pero como máximo tres de ellas son independientes: si se multiplican los lados "horarios" de tres de ellas y se infiere que el producto es igual al producto de los lados "antihorarios" de las mismas tres identidades, y luego se cancelan los factores comunes de ambos lados, el resultado es la cuarta identidad.

Tres ángulos son los ángulos de algún triángulo si y sólo si su suma es 180° (π radianes). ¿Qué condición sobre 12 ángulos es necesaria y suficiente para que sean los 12 ángulos de algún tetraedro? Claramente la suma de los ángulos de cualquier lado del tetraedro debe ser 180°. Como hay cuatro triángulos de este tipo, hay cuatro restricciones de este tipo sobre las sumas de ángulos, y el número de grados de libertad se reduce así de 12 a 8. Las cuatro relaciones dadas por esta ley del seno reducen aún más el número de grados de libertad, de 8 a no 4 sino a 5, ya que la cuarta restricción no es independiente de las tres primeras. Por lo tanto, el espacio de todas las formas de los tetraedros es de cinco dimensiones. ^[30]

Sean , , , los puntos de un tetraedro. Sea el área de la cara opuesta al vértice y sea el ángulo diedro entre las dos caras del tetraedro adyacentes a la arista . La ley de los cosenos para un tetraedro, que relaciona las áreas de las caras del tetraedro con los ángulos diedros respecto de un vértice, viene dada por la siguiente relación: ^[31]${\displaystyle P_{1}}$${\displaystyle P_{2}}$${\displaystyle P_{3}}$${\displaystyle P_{4}}$${\displaystyle \Delta _{i}}$${\displaystyle P_{i}}$${\displaystyle \theta _{ij}}$${\displaystyle P_{i}P_{j}}$$${\displaystyle \Delta _{i}^{2}=\Delta _{j}^{2}+\Delta _{k}^{2}+\Delta _{l}^{2}-2(\Delta _{j}\Delta _{k}\cos \theta _{il}+\Delta _{j}\Delta _{l}\cos \theta _{ik}+\Delta _{k}\Delta _{l}\cos \theta _{ij})}$$

Sea P cualquier punto interior de un tetraedro de volumen V cuyos vértices son A , B , C y D , y cuyas áreas de las caras opuestas son F _a , F _b , F _c y F _d . Entonces ^{[32] : p.62, #1609}

${\displaystyle PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} }\geq 9V.}$

Para los vértices A , B , C y D , el punto interior P y los pies J , K , L y M de las perpendiculares desde P a las caras, y supongamos que las caras tienen áreas iguales, entonces ^{[32] : p.226, #215}

${\displaystyle PA+PB+PC+PD\geq 3(PJ+PK+PL+PM).}$

Denotando el radio interior de un tetraedro como r y los radios interiores de sus caras triangulares como r _i para i = 1, 2, 3, 4, tenemos ^{[32] : p.81, #1990}

${\displaystyle {\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3}^{2}}}+{\frac {1}{r_{4}^{2}}}\leq {\frac {2}{r^{2}}},}$

con igualdad si y sólo si el tetraedro es regular.

Si A ₁ , A ₂ , A ₃ y A ₄ denotan el área de cada cara, el valor de r viene dado por

${\displaystyle r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}}$.

Esta fórmula se obtiene al dividir el tetraedro en cuatro tetraedros cuyos puntos son los tres puntos de una de las caras originales y el incentro. Como los cuatro subtetraedros llenan el volumen, tenemos .${\displaystyle V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{4}r}$

Denotemos el radio circunscrito de un tetraedro como R. Sean a , b , c las longitudes de las tres aristas que se encuentran en un vértice, y A , B , C las longitudes de las aristas opuestas. Sea V el volumen del tetraedro. Entonces ^{[33] [34]}

${\displaystyle R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.}$

El circuncentro de un tetraedro se puede hallar como la intersección de tres planos bisectrices. Un plano bisectrices se define como el plano centrado en, y ortogonal a, una arista del tetraedro. Con esta definición, el circuncentro C de un tetraedro con vértices x ₀ , x ₁ , x ₂ , x ₃ se puede formular como producto matriz-vector: ^[35]

${\displaystyle {\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0}\right]^{T}\\\left[x_{2}-x_{0}\right]^{T}\\\left[x_{3}-x_{0}\right]^{T}\end{matrix}}\right)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrix}\|x_{1}\|^{2}-\|x_{0}\|^{2}\\\|x_{2}\|^{2}-\|x_{0}\|^{2}\\\|x_{3}\|^{2}-\|x_{0}\|^{2}\end{matrix}}\right)\\\end{aligned}}}$

A diferencia del baricentro, el circuncentro no siempre se encuentra en el interior de un tetraedro. De manera análoga a un triángulo obtusángulo, en el caso de un tetraedro obtusángulo el circuncentro se encuentra fuera del objeto.

El centro de masa del tetraedro se puede calcular como la media aritmética de sus cuatro vértices, véase Centroide .

La suma de las áreas de tres caras cualesquiera es mayor que el área de la cuarta cara. ^{[32] : p.225, #159}

Existen tetraedros que tienen longitudes de aristas, áreas de caras y volúmenes de valores enteros. Estos se llaman tetraedros heronianos . Un ejemplo tiene una arista de 896, la arista opuesta de 990 y las otras cuatro aristas de 1073; dos caras son triángulos isósceles con áreas de436 800 y los otros dos son isósceles con áreas de47 120 , mientras que el volumen es124 185 600 . ^[36]

Un tetraedro puede tener volumen entero y números enteros consecutivos como aristas, siendo un ejemplo el que tiene las aristas 6, 7, 8, 9, 10 y 11 y volumen 48. ^[37]

Un tetraedro regular puede verse como una pirámide triangular .

Pirámides regulares
Digonal	Triangular	Cuadrado	Pentagonal	Hexagonal	Heptagonal	...
Incorrecto	Regular	Equilátero		Isósceles
						...
						...

Un tetraedro regular puede verse como un poliedro degenerado, un antiprisma digonal uniforme , donde los polígonos base son digones reducidos .

Familia de antiprismas n- gonales uniformes

• en
• a
• mi

Nombre del antiprisma	Antiprisma digonal	Antiprisma triangular (trigonal)	Antiprisma cuadrado (tetragonal)	Antiprisma pentagonal	Antiprisma hexagonal	Antiprisma heptagonal	...	Antiprisma apeirogonal
Imagen de poliedro							...
Imagen de mosaico esférico							Imagen de mosaico plano
Configuración de vértice.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

Un tetraedro regular puede verse como un poliedro degenerado, un trapezoedro diagonal dual uniforme , que contiene 6 vértices, en dos conjuntos de aristas colineales.

Familia de trapezoedros n -gonales

Nombre del trapezoedro	Trapezoedro digonal (Tetraedro)	Trapezoedro trigonal	Trapezoedro tetragonal	Trapezoedro pentagonal	Trapezoedro hexagonal	...	Trapezoedro apeirogonal
Imagen de poliedro						...
Imagen de mosaico esférico						Imagen de mosaico plano
Configuración de la cara	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	...	V∞.3.3.3

Un proceso de truncamiento aplicado al tetraedro produce una serie de poliedros uniformes . El truncamiento de las aristas hasta convertirlas en puntos produce el octaedro como un tetraedro rectificado. El proceso se completa como una birectificación, reduciendo las caras originales hasta convertirlas en puntos y produciendo nuevamente el tetraedro autodual.

Familia de poliedros tetraédricos uniformes
Simetría : [3,3] , (*332)							[3,3] + , (332)
{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
De poliedros duales a uniformes
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros regulares con símbolos de Schläfli {3, n }, que continúan en el plano hiperbólico .

* n 32 mutación de simetría de teselaciones regulares: {3, n } en a mi
Esférico				Euclides.	Hiper compacto.		Paraíso.	Hiperbólica no compacta
3.3	33	3 4	3 5	3 6	3 7	3 8	3 ∞	3 12i	3 9i	3 6i	3 3i

El tetraedro está relacionado topológicamente con una serie de poliedros regulares y teselas con figuras de vértices de orden 3 .

* n 32 mutación de simetría de teselaciones regulares: { n ,3} en a mi
Esférico				Euclidiano	Hiperb. compacta.		Paraíso.	Hiperbólica no compacta
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

• Compuestos de tetraedros
• 
  Dos tetraedros en un cubo
• 
  Compuesto de cinco tetraedros
• 
  Compuesto de diez tetraedros

Se puede construir un interesante poliedro a partir de cinco tetraedros que se intersecan . Este compuesto de cinco tetraedros se conoce desde hace cientos de años y aparece con regularidad en el mundo del origami . Uniendo los veinte vértices se formaría un dodecaedro regular . Hay formas tanto levógiras como diestras , que son imágenes especulares una de la otra. Al superponer ambas formas se obtiene un compuesto de diez tetraedros , en el que los diez tetraedros están dispuestos como cinco pares de estrellas octangulares . Una estrella octangular es un compuesto de dos tetraedros en posición dual y sus ocho vértices definen un cubo como su envoltura convexa.

El hosoedro cuadrado es otro poliedro con cuatro caras, pero no tiene caras triangulares.

El poliedro de Szilassi y el tetraedro son los únicos dos poliedros conocidos en los que cada cara comparte una arista con las demás caras. Además, el poliedro de Császár (que es el doble del poliedro de Szilassi) y el tetraedro son los únicos dos poliedros conocidos en los que todas las diagonales se encuentran en los lados.

En el análisis numérico , las formas tridimensionales complicadas se descomponen comúnmente en, o se aproximan mediante, una malla poligonal de tetraedros irregulares en el proceso de configuración de las ecuaciones para el análisis de elementos finitos , especialmente en la solución numérica de ecuaciones diferenciales parciales . Estos métodos tienen amplias aplicaciones en aplicaciones prácticas en dinámica de fluidos computacional , aerodinámica , campos electromagnéticos , ingeniería civil , ingeniería química , arquitectura e ingeniería naval y campos relacionados.

Un tetraedro con bordes rígidos es inherentemente rígido. Por este motivo, se lo suele utilizar para reforzar estructuras de armazón, como las espaciales .

Los tetraedros se utilizan en abrojos para proporcionar un arma de negación de área . Esto se debe a su naturaleza de tener una esquina afilada que siempre apunta hacia arriba.

Se han utilizado grandes tetraedros de hormigón como medidas antitanque o como tetrápodos para romper las olas en las costas.

En algunos aeródromos , un gran marco en forma de tetraedro con dos lados cubiertos con un material fino está montado sobre un pivote giratorio y siempre apunta hacia el viento. Es lo suficientemente grande para ser visto desde el aire y a veces está iluminado. Su propósito es servir como referencia para los pilotos que indican la dirección del viento. ^[38]

La forma tetraédrica se observa en la naturaleza en moléculas unidas covalentemente . Todos los átomos con hibridación ^sp3 están rodeados por átomos (o pares de electrones solitarios ) en las cuatro esquinas de un tetraedro. Por ejemplo, en una molécula de metano ( CH
₄) o un ion amonio ( NH⁺
₄), cuatro átomos de hidrógeno rodean un átomo central de carbono o nitrógeno con simetría tetraédrica. Por esta razón, una de las principales revistas de química orgánica se llama Tetrahedron . El ángulo central entre dos vértices cualesquiera de un tetraedro perfecto es arccos(− ⁠1/3) , o aproximadamente 109,47°. ^[39]

Agua , H
₂El O , también tiene una estructura tetraédrica, con dos átomos de hidrógeno y dos pares de electrones solitarios alrededor de los átomos de oxígeno centrales. Sin embargo, su simetría tetraédrica no es perfecta, porque los pares solitarios se repelen más que los enlaces O–H simples.

Los diagramas de fases cuaternarias de mezclas de sustancias químicas se representan gráficamente como tetraedros.

Sin embargo, los diagramas de fases cuaternarias en ingeniería de comunicaciones se representan gráficamente en un plano bidimensional.

Existen moléculas con forma basada en cuatro átomos próximos cuyos enlaces forman los lados de una estructura tetraédrica, como el alótropo del fósforo blanco ^[40] y el tetra- t -butiltetrahedrano, conocido derivado del hipotético tetrahedrano .

Si se sueldan seis resistencias iguales para formar un tetraedro, entonces la resistencia medida entre dos vértices es la mitad de la de una resistencia. ^[41]

Dado que el silicio es el semiconductor más común utilizado en la electrónica de estado sólido , y el silicio tiene una valencia de cuatro, la forma tetraédrica de los cuatro enlaces químicos del silicio tiene una fuerte influencia en cómo se forman los cristales de silicio y qué formas adoptan.

Los tetraedros se utilizan en algoritmos de conversión del espacio de color específicamente para casos en los que el eje de luminancia segmenta diagonalmente el espacio de color (por ejemplo, RGB, CMY). ^[42]

El Juego Real de Ur , que data del año 2600 a. C., se jugaba con un juego de dados tetraédricos.

Especialmente en los juegos de rol , este sólido se conoce como dado de 4 caras , uno de los dados poliédricos más comunes , en el que el número que sale aparece en la parte inferior o en el vértice superior. Algunos rompecabezas similares al cubo de Rubik son tetraédricos, como el Pyraminx y el Pyramorphix .

La hipótesis tetraédrica , publicada originalmente por William Lowthian Green para explicar la formación de la Tierra, ^[43] fue popular hasta principios del siglo XX. ^{[44] [45]}

Según Marvin Minsky , un científico cognitivo y experto en inteligencia artificial que asesoró a Kubrick sobre la computadora HAL 9000 y otros aspectos de la película, Stanley Kubrick originalmente pretendía que el monolito de 2001: Odisea del espacio fuera un tetraedro. Kubrick descartó la idea de usar el tetraedro porque un visitante que vio imágenes de él no reconoció lo que era y no quería nada en la película que la gente común no entendiera. ^[46]

El tetraedro con caras regulares es una solución a un viejo acertijo que pedía formar cuatro triángulos equiláteros utilizando seis cerillas enteras. La solución coloca las cerillas a lo largo de los bordes de un tetraedro. ^[47]

Gráfica tetraédrica
Vértices	4
Bordes	6
Radio	1
Diámetro	1
Circunferencia	3
Automorfismos	24
Número cromático	4
Propiedades	Hamiltoniano , regular , simétrico , regular en relación con la distancia , transitivo en relación con la distancia , conectado con 3 vértices , gráfico plano
Tabla de gráficos y parámetros

El esqueleto del tetraedro (que comprende los vértices y las aristas) forma un grafo , con 4 vértices y 6 aristas. Es un caso especial del grafo completo , K ₄ , y del grafo de rueda , W ₄ . ^[48] Es uno de los 5 grafos platónicos , cada uno un esqueleto de su sólido platónico .

Simetría triple

• Hélice de Boerdijk-Coxeter
• Configuración de Möbius
• Abrojo
• Semihipercubo y símplex : análogos n -dimensionales
• Pentachoron – análogo de 4 dimensiones
• Sinergética (Fuller)
• Cometa tetraédrica
• Número tetraédrico
• Tetraedroide
• Empaquetamiento tetraédrico
• Bipirámide triangular : construida uniendo dos tetraedros a lo largo de una cara.
• Tetraedro trirectangular
• Ortoesquema

Wikimedia Commons tiene medios relacionados con Tetraedro .

• Weisstein, Eric W. "Tetraedro". MathWorld .
• Modelos de papel gratuitos de un tetraedro y muchos otros poliedros
• Un asombroso tetraedro no regular que llena el espacio y que también incluye una descripción de un "anillo giratorio de tetraedros", también conocido como caleidociclo .