Poliedro de Szilassi
| Poliedro de Szilassi | |
|---|---|
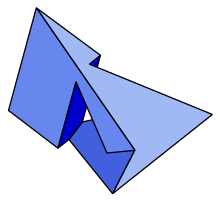 | |
| Tipo | Poliedro toroidal |
| Caras | 7 hexágonos |
| Bordes | 21 |
| Vértices | 14 |
| Carácter de Euler. | 0 (Género 1) |
| Configuración de vértice | 6.6.6 |
| Grupo de simetría | C 1 , [ ] + , (11) |
| Poliedro dual | Poliedro de Császár |
| Propiedades | No convexo |
En geometría , el poliedro de Szilassi es un poliedro no convexo , topológicamente un toro , con siete caras hexagonales .
Coloración y simetría
Los 14 vértices y 21 aristas del poliedro de Szilassi forman una incrustación del grafo de Heawood sobre la superficie de un toro. [1] Cada cara de este poliedro comparte una arista con cada una de las otras caras. Como resultado, se requieren siete colores para colorear todas las caras adyacentes. Este ejemplo muestra que, en superficies topológicamente equivalentes a un toro , algunas subdivisiones requieren siete colores, lo que proporciona el límite inferior para el teorema de los siete colores . La otra mitad del teorema establece que todas las subdivisiones toroidales se pueden colorear con siete colores o menos.
El poliedro de Szilassi tiene un eje de simetría de 180 grados . Esta simetría intercambia tres pares de caras congruentes, lo que deja un hexágono no apareado que tiene la misma simetría rotacional que el poliedro.
Adyacencia facial completa
El tetraedro y el poliedro de Szilassi son los dos únicos poliedros conocidos en los que cada cara comparte una arista con cada una de las otras caras.
Si un poliedro con f caras se incrusta en una superficie con h agujeros, de tal manera que cada cara comparte una arista con cada una de las otras caras, se deduce, mediante alguna manipulación de la característica de Euler , que
Esta ecuación se satisface para el tetraedro con h = 0 y f = 4, y para el poliedro de Szilassi con h = 1 y f = 7.
La siguiente solución posible, h = 6 y f = 12, correspondería a un poliedro con 44 vértices y 66 aristas. Sin embargo, no se sabe si un poliedro de este tipo puede realizarse geométricamente sin autocruces (en lugar de como un politopo abstracto ). De manera más general, esta ecuación puede satisfacerse con precisión cuando f es congruente con 0, 3, 4 o 7 módulo 12. [2] [3]
- Proyección ortográfica interactiva con cada cara de un color diferente. En la imagen SVG, mueva el ratón hacia la izquierda y hacia la derecha para rotar el modelo.
- Animación
Historia
El poliedro Szilassi lleva el nombre del matemático húngaro Lajos Szilassi , quien lo descubrió en 1977. [4] [1] El dual del poliedro Szilassi, el poliedro de Császár , fue descubierto anteriormente por Ákos Császár (1949); tiene siete vértices, 21 aristas que conectan cada par de vértices y 14 caras triangulares. Al igual que el poliedro de Szilassi, el poliedro de Császár tiene la topología de un toroide. [5]
Referencias
- ^ ab Szilassi, Lajos (1986), "Toroides regulares" (PDF) , Topología estructural , 13 : 69–80
- ^ Jüngerman, M.; Ringel, Gerhard (1980), "Triangulaciones mínimas en superficies orientables", Acta Mathematica , 145 (1–2): 121–154, doi : 10.1007/BF02414187
- ^ Grünbaum, Branko ; Szilassi, Lajos (2009), "Realizaciones geométricas de complejos toroidales especiales", Contribuciones a las matemáticas discretas , 4 (1): 21–39, doi : 10.11575/cdm.v4i1.61986 , MR 2541986
- ^ Gardner, Martin (1978), "En el que se aplica una estética matemática al arte minimalista moderno", Mathematical Games, Scientific American , 239 (5): 22–32, doi :10.1038/scientificamerican1178-22, JSTOR 24955839
- ^ Császár, Ákos (1949), "Un poliedro sin diagonales", Acta Sci. Matemáticas. Szeged , 13 : 140-142
Enlaces externos
- Ace, Tom, El poliedro Szilassi.
- Peterson, Ivars (2007), "Un poliedro con un agujero", MathTrek, Asociación Matemática de América.
- Weisstein, Eric W. , "Poliedro de Szilassi", MathWorld
- Poliedro Szilassi – Modelo de Papercraft en CutOutFoldUp.com

