Estado cuántico

Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Número cuántico Estado Superposición Simetría Túnel Incertidumbre Función de onda Colapsar
Experimentos Desigualdad de Bell Desigualdad de CHSH Davisson-Germer Doble rendija Elitzur–Vaidman Franck-Hertz Desigualdad de Leggett Desigualdad de Leggett-Garg Mach–Zehnder Corchete Borrador cuántico Elección retrasada El gato de Schrödinger Stern–Gerlach La elección retrasada de Wheeler
Formulaciones Descripción general Heisenberg Interacción Matriz Espacio de fases Schrödinger Suma de historias (integral de trayectoria)
Ecuaciones Dirac Klein-Gordon Pablo Rydberg Schrödinger
Interpretaciones Bayesiano Historias consistentes Copenhague de Broglie–Bohm Conjunto Variable oculta Local Superdeterminismo Muchos mundos Colapso objetivo Lógica cuántica Relacional Transaccional De von Neumann-Wigner
Temas avanzados Mecánica cuántica relativista Teoría cuántica de campos Ciencia de la información cuántica Computación cuántica Caos cuántico Paradoja del EPR Matriz de densidad Teoría de la dispersión Mecánica estadística cuántica Aprendizaje automático cuántico
Científicos Aharonov Campana Bethe Negro Bloqueo Bóhm Bohr Nacido Bosé de Broglie Compton Dirac Davison Debye Fiesta de los testigos Einstein Everett Follar Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordán Kramer Cordero Landó Laue Mosley Millikan Onnas Pablo Planck Rabí Rama Rydberg Schrödinger Simmons Campo de verano de Neumann Weyl Viena Wigner Zeeman Zeilinger
v t e

En física cuántica , un estado cuántico es una entidad matemática que incorpora el conocimiento de un sistema cuántico. La mecánica cuántica especifica la construcción, evolución y medición de un estado cuántico. El resultado es una predicción para el sistema representado por el estado. El conocimiento del estado cuántico y las reglas para la evolución del sistema en el tiempo agotan todo lo que se puede saber sobre un sistema cuántico.

Los estados cuánticos pueden definirse de manera diferente para distintos tipos de sistemas o problemas. Dos grandes categorías son:

• Funciones de onda que describen sistemas cuánticos utilizando variables de posición o momento y
• los estados cuánticos vectoriales más abstractos.

Los problemas históricos, educativos y de aplicación suelen incluir funciones de onda; la física profesional moderna utiliza los estados vectoriales abstractos. En ambas categorías, los estados cuánticos se dividen en estados puros y mixtos, o en estados coherentes y estados incoherentes. Las categorías con propiedades especiales incluyen estados estacionarios para independencia temporal y estados de vacío cuántico en la teoría cuántica de campos .

Como herramienta para la física, los estados cuánticos surgieron de los estados de la mecánica clásica . Un estado dinámico clásico consiste en un conjunto de variables dinámicas con valores reales bien definidos en cada instante de tiempo. ^{[1] : 3} Por ejemplo, el estado de una bala de cañón consistiría en su posición y velocidad. Los valores del estado evolucionan bajo ecuaciones de movimiento y, por lo tanto, permanecen estrictamente determinados. Si conocemos la posición de un cañón y la velocidad de salida de sus proyectiles, entonces podemos usar ecuaciones que contengan la fuerza de la gravedad para predecir la trayectoria de una bala de cañón con precisión.

De manera similar, los estados cuánticos consisten en conjuntos de variables dinámicas que evolucionan bajo ecuaciones de movimiento. Sin embargo, los valores derivados de los estados cuánticos son números complejos , cuantizados, limitados por relaciones de incertidumbre , ^{[1] : 159} y solo proporcionan una distribución de probabilidad para los resultados de un sistema. Estas restricciones alteran la naturaleza de las variables dinámicas cuánticas. Por ejemplo, el estado cuántico de un electrón en un experimento de doble rendija consistiría en valores complejos sobre la región de detección y, cuando se eleva al cuadrado, solo predeciría la distribución de probabilidad de los recuentos de electrones a través del detector.

El proceso de descripción de un sistema cuántico con mecánica cuántica comienza con la identificación de un conjunto de variables que definen el estado cuántico del sistema. ^{[1] : 204} El conjunto contendrá variables compatibles e incompatibles . La medición simultánea de un conjunto completo de variables compatibles prepara el sistema en un estado único. El estado luego evoluciona de manera determinista de acuerdo con las ecuaciones de movimiento . La medición posterior del estado produce una muestra de una distribución de probabilidad predicha por el operador mecánico cuántico correspondiente a la medición.

La naturaleza fundamentalmente estadística o probabilística de las mediciones cuánticas cambia el papel de los estados cuánticos en la mecánica cuántica en comparación con los estados clásicos en la mecánica clásica. En la mecánica clásica, se mide el estado inicial de uno o más cuerpos; el estado evoluciona de acuerdo con las ecuaciones de movimiento; las mediciones del estado final se comparan con las predicciones. En la mecánica cuántica, conjuntos de estados cuánticos preparados de manera idéntica evolucionan de acuerdo con las ecuaciones de movimiento y muchas mediciones repetidas se comparan con distribuciones de probabilidad predichas. ^{[1] : 204}

Las mediciones, operaciones macroscópicas sobre estados cuánticos, filtran el estado. ^{[1] : 196} Cualquiera que sea el estado cuántico de entrada, las mediciones idénticas repetidas dan valores consistentes. Por esta razón, las mediciones 'preparan' los estados cuánticos para los experimentos, colocando el sistema en un estado parcialmente definido. Las mediciones posteriores pueden preparar aún más el sistema (estas son mediciones compatibles) o pueden alterar el estado, redefiniéndolo (estas se denominan mediciones incompatibles o complementarias). Por ejemplo, podemos medir el momento de un estado a lo largo del eje cualquier número de veces y obtener el mismo resultado, pero si medimos la posición después de medir una vez el momento, las mediciones posteriores del momento cambian. El estado cuántico parece inevitablemente alterado por mediciones incompatibles. Esto se conoce como el principio de incertidumbre .${\displaystyle x}$

El estado cuántico después de una medición se encuentra en un estado propio correspondiente a esa medición y al valor medido. ^{[1] : 202} Otros aspectos del estado pueden ser desconocidos. Repetir la medición no alterará el estado. En algunos casos, las mediciones compatibles pueden refinar aún más el estado, haciendo que sea un estado propio correspondiente a todas estas mediciones. ^[2] Un conjunto completo de mediciones compatibles produce un estado puro . Cualquier estado que no sea puro se denomina estado mixto , como se analiza en mayor profundidad a continuación. ^{[1] : 204  [3] : 73}

Las soluciones de estado propio de la ecuación de Schrödinger se pueden transformar en estados puros. Los experimentos rara vez producen estados puros. Por lo tanto, las mezclas estadísticas de soluciones deben compararse con los experimentos. ^{[1] : 204}

El mismo estado cuántico físico se puede expresar matemáticamente de diferentes maneras llamadas representaciones . ^[1] La función de onda de posición es una representación que a menudo se ve primero en las introducciones a la mecánica cuántica. La función de onda de momento equivalente es otra representación basada en la función de onda. Las representaciones son análogas a los sistemas de coordenadas ^{[1] : 244} o dispositivos matemáticos similares como las ecuaciones paramétricas . Seleccionar una representación hará que algunos aspectos de un problema sean más fáciles a costa de dificultar otros.

En la mecánica cuántica formal (ver más abajo) la teoría se desarrolla en términos de un " espacio vectorial " abstracto, evitando cualquier representación particular. Esto permite expresar y aplicar muchos conceptos elegantes de la mecánica cuántica incluso en casos en los que no existe un análogo clásico. ^{[1] : 244}

Las funciones de onda representan estados cuánticos, particularmente cuando son funciones de posición o de momento . Históricamente, las definiciones de estados cuánticos usaban funciones de onda antes de que se desarrollaran los métodos más formales. ^{[4] : 268} La función de onda es una función de valor complejo de cualquier conjunto completo de grados de libertad compatibles o conmutativos . Por ejemplo, un conjunto podría ser las coordenadas espaciales de un electrón. La preparación de un sistema midiendo el conjunto completo de observables compatibles produce un estado cuántico puro . Más común, la preparación incompleta produce un estado cuántico mixto . Las soluciones de función de onda de las ecuaciones de movimiento de Schrödinger para operadores correspondientes a mediciones se pueden expresar fácilmente como estados puros; deben combinarse con pesos estadísticos que coincidan con la preparación experimental para calcular la distribución de probabilidad esperada. ^{[1] : 205}${\displaystyle x,y,z}$

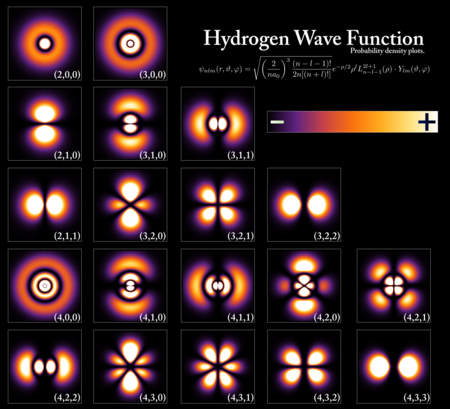
Las soluciones numéricas o analíticas en mecánica cuántica se pueden expresar como estados puros . Estos estados de solución, llamados estados propios , se etiquetan con valores cuantizados, típicamente números cuánticos . Por ejemplo, cuando se trata del espectro de energía del electrón en un átomo de hidrógeno , los estados puros relevantes se identifican por el número cuántico principal n , el número cuántico del momento angular ℓ , el número cuántico magnético m y el componente z de espín s _z . Para otro ejemplo, si se mide el espín de un electrón en cualquier dirección, por ejemplo con un experimento de Stern-Gerlach , hay dos resultados posibles: hacia arriba o hacia abajo. Un estado puro aquí se representa por un vector complejo bidimensional , con una longitud de uno; es decir, con donde y son los valores absolutos de y .${\displaystyle (\alpha ,\beta )}$$${\displaystyle |\alpha |^{2}+|\beta |^{2}=1,}$$${\displaystyle |\alpha |}$${\displaystyle |\beta |}$${\displaystyle \alpha }$${\displaystyle \beta }$

Los postulados de la mecánica cuántica establecen que los estados puros, en un tiempo dado t , corresponden a vectores en un espacio de Hilbert complejo separable , mientras que cada cantidad física medible (como la energía o el momento de una partícula ) está asociada a un operador matemático llamado observable . El operador sirve como una función lineal que actúa sobre los estados del sistema. Los valores propios del operador corresponden a los posibles valores del observable. Por ejemplo, es posible observar una partícula con un momento de 1 kg⋅m/s si y solo si uno de los valores propios del operador de momento es 1 kg⋅m/s. El vector propio correspondiente (que los físicos llaman estado propio ) con valor propio 1 kg⋅m/s sería un estado cuántico con un valor de momento definido y bien definido de 1 kg⋅m/s, sin incertidumbre cuántica . Si se midiera su momento, se garantiza que el resultado sea 1 kg⋅m/s.

Por otra parte, un estado puro descrito como una superposición de múltiples estados propios diferentes tiene en general incertidumbre cuántica para el observable dado. Usando la notación bra–ket , esta combinación lineal de estados propios puede representarse como: ^{[5] : 22, 171, 172} El coeficiente que corresponde a un estado particular en la combinación lineal es un número complejo, permitiendo así efectos de interferencia entre estados. Los coeficientes dependen del tiempo. La forma en que un estado cuántico cambia en el tiempo está gobernada por el operador de evolución temporal .$${\displaystyle |\Psi (t)\rangle =\sum _{n}C_{n}(t)|\Phi _{n}\rangle .}$$

Un estado cuántico mixto corresponde a una mezcla probabilística de estados puros; sin embargo, diferentes distribuciones de estados puros pueden generar estados mixtos equivalentes (es decir, físicamente indistinguibles). Una mezcla de estados cuánticos es nuevamente un estado cuántico.

Un estado mixto para espines de electrones, en la formulación de matriz de densidad, tiene la estructura de una matriz que es hermítica y semidefinida positiva, y tiene traza 1. ^[6] Un caso más complicado se da (en notación bra-ket ) por el estado singlete , que ejemplifica el entrelazamiento cuántico : que involucra la superposición de estados de espín conjuntos para dos partículas con espín 1 ⁄ 2 . El estado singlete satisface la propiedad de que si los espines de las partículas se miden a lo largo de la misma dirección, entonces el espín de la primera partícula se observa hacia arriba y el espín de la segunda partícula se observa hacia abajo, o bien la primera se observa hacia abajo y la segunda se observa hacia arriba, ocurriendo ambas posibilidades con igual probabilidad.${\displaystyle 2\times 2}$$${\displaystyle \left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigl (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigr )},}$$

Un estado cuántico puro puede representarse mediante un rayo en un espacio de Hilbert proyectivo sobre los números complejos , mientras que los estados mixtos se representan mediante matrices de densidad , que son operadores semidefinidos positivos que actúan sobre espacios de Hilbert. ^{[7] [3]} El teorema de Schrödinger-HJW clasifica la multitud de formas de escribir un estado mixto dado como una combinación convexa de estados puros. ^[8] Antes de que se realice una medición particular en un sistema cuántico, la teoría solo proporciona una distribución de probabilidad para el resultado, y la forma que toma esta distribución está completamente determinada por el estado cuántico y los operadores lineales que describen la medición. Las distribuciones de probabilidad para diferentes mediciones exhiben compensaciones ejemplificadas por el principio de incertidumbre : un estado que implica una estrecha dispersión de posibles resultados para un experimento implica necesariamente una amplia dispersión de posibles resultados para otro.

Las mezclas estadísticas de estados son un tipo diferente de combinación lineal. Una mezcla estadística de estados es un conjunto estadístico de sistemas independientes. Las mezclas estadísticas representan el grado de conocimiento, mientras que la incertidumbre dentro de la mecánica cuántica es fundamental. Matemáticamente, una mezcla estadística no es una combinación que utiliza coeficientes complejos, sino más bien una combinación que utiliza probabilidades positivas de valor real de diferentes estados . Un número representa la probabilidad de que un sistema seleccionado al azar se encuentre en el estado . A diferencia del caso de la combinación lineal, cada sistema se encuentra en un estado propio definido. ^{[9] [10]}${\displaystyle \Phi _{n}}$${\displaystyle P_{n}}$${\displaystyle \Phi _{n}}$

El valor esperado de un observable A es una media estadística de los valores medidos del observable. Es esta media y la distribución de probabilidades lo que predicen las teorías físicas.${\displaystyle {\langle A\rangle }_{\sigma }}$

No existe ningún estado que sea simultáneamente un estado propio para todos los observables. Por ejemplo, no podemos preparar un estado tal que tanto la medida de posición Q ( t ) como la medida de momento P ( t ) (al mismo tiempo t ) se conozcan con exactitud; al menos una de ellas tendrá un rango de valores posibles. ^[a] Este es el contenido de la relación de incertidumbre de Heisenberg .

Además, a diferencia de la mecánica clásica, es inevitable que realizar una medición en el sistema generalmente cambie su estado . ^{[11] [12] [13] : 4} Más precisamente: después de medir un observable A , el sistema estará en un estado propio de A ; por lo tanto, el estado ha cambiado, a menos que el sistema ya estuviera en ese estado propio. Esto expresa una especie de consistencia lógica: si medimos A dos veces en la misma ejecución del experimento, siendo las mediciones directamente consecutivas en el tiempo, ^[b] entonces producirán los mismos resultados. Sin embargo, esto tiene algunas consecuencias extrañas, como sigue.

Consideremos dos observables incompatibles , A y B , donde A corresponde a una medición anterior en el tiempo que B. ^[c] Supongamos que el sistema está en un estado propio de B al comienzo del experimento . Si medimos solo B , todas las ejecuciones del experimento arrojarán el mismo resultado. Si medimos primero A y luego B en la misma ejecución del experimento, el sistema se transferirá a un estado propio de A después de la primera medición, y generalmente notaremos que los resultados de B son estadísticos. Por lo tanto: Las mediciones mecánico-cuánticas se influyen entre sí , y el orden en el que se realizan es importante.

Otra característica de los estados cuánticos se vuelve relevante si consideramos un sistema físico que consta de múltiples subsistemas; por ejemplo, un experimento con dos partículas en lugar de una. La física cuántica permite ciertos estados, llamados estados entrelazados , que muestran ciertas correlaciones estadísticas entre las mediciones de las dos partículas que no pueden explicarse mediante la teoría clásica. Para más detalles, véase entrelazamiento . Estos estados entrelazados conducen a propiedades comprobables experimentalmente ( teorema de Bell ) que nos permiten distinguir entre la teoría cuántica y los modelos clásicos alternativos (no cuánticos).

Se puede considerar que los observables dependen del tiempo, mientras que el estado σ se fijó una vez al comienzo del experimento. Este enfoque se llama la imagen de Heisenberg . (Este enfoque se adoptó en la última parte de la discusión anterior, con observables variables en el tiempo P ( t ) , Q ( t ) .) Se puede, equivalentemente, tratar los observables como fijos, mientras que el estado del sistema depende del tiempo; esto se conoce como la imagen de Schrödinger . (Este enfoque se adoptó en la primera parte de la discusión anterior, con un estado variable en el tiempo ). Conceptualmente (y matemáticamente), los dos enfoques son equivalentes; elegir uno de ellos es una cuestión de convención.${\textstyle |\Psi (t)\rangle =\sum _{n}C_{n}(t)|\Phi _{n}\rangle }$

Ambos puntos de vista se utilizan en la teoría cuántica. Mientras que la mecánica cuántica no relativista suele formularse en términos de la imagen de Schrödinger, la imagen de Heisenberg suele preferirse en un contexto relativista, es decir, para la teoría cuántica de campos . Compárese con la imagen de Dirac . ^{[14] : 65}

La física cuántica se formula más comúnmente en términos de álgebra lineal , de la siguiente manera. Cualquier sistema dado se identifica con algún espacio de Hilbert de dimensión finita o infinita . Los estados puros corresponden a vectores de norma 1. Por lo tanto, el conjunto de todos los estados puros corresponde a la esfera unitaria en el espacio de Hilbert, porque la esfera unitaria se define como el conjunto de todos los vectores con norma 1.

Multiplicar un estado puro por un escalar es físicamente intrascendente (siempre que se considere el estado por sí mismo). Si un vector en un espacio de Hilbert complejo se puede obtener a partir de otro vector multiplicándolo por algún número complejo distinto de cero, se dice que los dos vectores en corresponden al mismo rayo en el espacio de Hilbert proyectivo de . Nótese que aunque se utiliza la palabra rayo , hablando propiamente, un punto en el espacio de Hilbert proyectivo corresponde a una línea que pasa por el origen del espacio de Hilbert, en lugar de una semilínea , o rayo en el sentido geométrico .${\displaystyle H}$${\displaystyle H}$ ${\displaystyle \mathbf {P} (H)}$${\displaystyle H}$

El momento angular tiene la misma dimensión ( M · L ² · T ⁻¹ ) que la constante de Planck y, a escala cuántica, se comporta como un grado discreto de libertad de un sistema cuántico. La mayoría de las partículas poseen un tipo de momento angular intrínseco que no aparece en absoluto en la mecánica clásica y surge de la generalización relativista de la teoría de Dirac. Matemáticamente se describe con espinores . En la mecánica cuántica no relativista, las representaciones de grupo del grupo de Lie SU(2) se utilizan para describir esta libertad adicional. Para una partícula dada, la elección de la representación (y, por lo tanto, el rango de valores posibles del observable de espín) está especificada por un número no negativo S que, en unidades de la constante de Planck reducida ħ , es un entero (0, 1, 2 ...) o un semientero (1/2, 3/2, 5/2 ...). Para una partícula masiva con espín S , su número cuántico de espín m siempre asume uno de los 2 S + 1 valores posibles en el conjunto $${\displaystyle \{-S,-S+1,\ldots ,S-1,S\}}$$

En consecuencia, el estado cuántico de una partícula con espín se describe mediante una función de onda vectorial con valores en C ^{2 S +1} . De manera equivalente, se representa mediante una función compleja de cuatro variables: a las tres variables continuas habituales (para la posición en el espacio) se añade una variable de número cuántico discreta (para el espín).

El estado cuántico de un sistema de N partículas, cada una potencialmente con espín, se describe mediante una función de valor complejo con cuatro variables por partícula, correspondientes a 3 coordenadas espaciales y espín , por ejemplo$${\displaystyle |\psi (\mathbf {r} _{1},\,m_{1};\;\dots ;\;\mathbf {r} _{N},\,m_{N})\rangle .}$$

Aquí, las variables de espín m _ν asumen valores del conjunto donde es el espín de la ν -ésima partícula para una partícula que no exhibe espín.$${\displaystyle \{-S_{\nu },\,-S_{\nu }+1,\,\ldots ,\,S_{\nu }-1,\,S_{\nu }\}}$$${\displaystyle S_{\nu }}$${\displaystyle S_{\nu }=0}$

El tratamiento de partículas idénticas es muy diferente para los bosones (partículas con espín entero) frente a los fermiones (partículas con espín semientero). La función de N partículas anterior debe ser simetrizada (en el caso bosónico) o antisimetrizada (en el caso fermiónico) con respecto al número de partículas. Si no todas las N partículas son idénticas, pero algunas de ellas lo son, entonces la función debe ser (anti)simetrizada por separado sobre las variables correspondientes a cada grupo de variables idénticas, de acuerdo con sus estadísticas (bosónicas o fermiónicas).

Los electrones son fermiones con S = 1/2 , los fotones (cuantos de luz) son bosones con S = 1 (aunque en el vacío no tienen masa y no se pueden describir con la mecánica de Schrödinger).

Cuando la simetrización o antisimetrización no es necesaria, los espacios de estados de N partículas se pueden obtener simplemente mediante productos tensoriales de espacios de una partícula, a lo que volveremos más adelante.

Un estado perteneciente a un espacio de Hilbert complejo separable siempre puede expresarse de forma única como una combinación lineal de elementos de una base ortonormal de . Utilizando la notación bra-ket , esto significa que cualquier estado puede escribirse como con coeficientes complejos y elementos de base . En este caso, la condición de normalización se traduce en En términos físicos, se ha expresado como una superposición cuántica de los "estados base" , es decir, los estados propios de un observable. En particular, si dicho observable se mide en el estado normalizado , entonces es la probabilidad de que el resultado de la medición sea . ^{[5] : 22}${\displaystyle |\psi \rangle }$ ${\displaystyle H}$${\displaystyle H}$${\displaystyle |\psi \rangle }$$${\displaystyle {\begin{aligned}|\psi \rangle &=\sum _{i}c_{i}|{k_{i}}\rangle ,\\&=\sum _{i}|{k_{i}}\rangle \langle k_{i}|\psi \rangle ,\end{aligned}}}$$ ${\displaystyle c_{i}=\langle {k_{i}}|\psi \rangle }$${\displaystyle |k_{i}\rangle }$$${\displaystyle \langle \psi |\psi \rangle =\sum _{i}\langle \psi |{k_{i}}\rangle \langle k_{i}|\psi \rangle =\sum _{i}\left|c_{i}\right|^{2}=1.}$$${\displaystyle |\psi \rangle }$${\displaystyle |{k_{i}}\rangle }$${\displaystyle |\psi \rangle }$$${\displaystyle |c_{i}|^{2}=|\langle {k_{i}}|\psi \rangle |^{2},}$$${\displaystyle k_{i}}$

En general, la expresión de probabilidad siempre consiste en una relación entre el estado cuántico y una porción del espectro de la variable dinámica (es decir, variable aleatoria ) que se observa. ^{[15] : 98  [16] : 53} Por ejemplo, la situación anterior describe el caso discreto ya que los valores propios pertenecen al espectro puntual . Del mismo modo, la función de onda es simplemente la función propia del operador hamiltoniano con los valores propios correspondientes ; la energía del sistema.${\displaystyle k_{i}}$${\displaystyle E}$

Un ejemplo del caso continuo lo da el operador de posición . La medida de probabilidad para un sistema en estado viene dada por: ^[17] donde es la función de densidad de probabilidad para encontrar una partícula en una posición dada. Estos ejemplos enfatizan la distinción en las características entre el estado y el observable. Es decir, mientras que es un estado puro que pertenece a , los vectores propios (generalizados) del operador de posición no lo son . ^[18]${\displaystyle \psi }$$${\displaystyle \mathrm {Pr} (x\in B|\psi )=\int _{B\subset \mathbb {R} }|\psi (x)|^{2}dx,}$$${\displaystyle |\psi (x)|^{2}}$${\displaystyle \psi }$${\displaystyle H}$

Aunque están estrechamente relacionados, los estados puros no son lo mismo que los estados ligados que pertenecen al espectro puntual puro de un observable sin incertidumbre cuántica. Se dice que una partícula está en un estado ligado si permanece localizada en una región acotada del espacio en todo momento. Un estado puro se denomina estado ligado si y solo si para cada hay un conjunto compacto tal que para todo . ^[19] La integral representa la probabilidad de que una partícula se encuentre en una región acotada en cualquier momento . Si la probabilidad permanece arbitrariamente cercana a entonces se dice que la partícula permanece en .${\displaystyle |\phi \rangle }$${\displaystyle \varepsilon >0}$ ${\displaystyle K\subset \mathbb {R} ^{3}}$$${\displaystyle \int _{K}|\phi (\mathbf {r} ,t)|^{2}\,\mathrm {d} ^{3}\mathbf {r} \geq 1-\varepsilon }$$${\displaystyle t\in \mathbb {R} }$${\displaystyle K}$${\displaystyle t}$${\displaystyle 1}$${\displaystyle K}$

Como se mencionó anteriormente, los estados cuánticos pueden superponerse . Si y son dos kets correspondientes a estados cuánticos, el ket también es un estado cuántico del mismo sistema. Tanto y pueden ser números complejos; su amplitud relativa y fase relativa influirán en el estado cuántico resultante. ${\displaystyle |\alpha \rangle }$${\displaystyle |\beta \rangle }$$${\displaystyle c_{\alpha }|\alpha \rangle +c_{\beta }|\beta \rangle }$$${\displaystyle c_{\alpha }}$${\displaystyle c_{\beta }}$

Al escribir el estado superpuesto usando y definiendo la norma del estado como: y extrayendo los factores comunes se obtiene: El factor de fase general al frente no tiene efecto físico. ^{[20] : 108} Solo la fase relativa afecta la naturaleza física de la superposición.$${\displaystyle c_{\alpha }=A_{\alpha }e^{i\theta _{\alpha }}\ \ c_{\beta }=A_{\beta }e^{i\theta _{\beta }}}$$$${\displaystyle |c_{\alpha }|^{2}+|c_{\beta }|^{2}=A_{\alpha }^{2}+A_{\beta }^{2}=1}$$$${\displaystyle e^{i\theta _{\alpha }}\left(A_{\alpha }|\alpha \rangle +{\sqrt {1-A_{\alpha }^{2}}}e^{i\theta _{\beta }-i\theta _{\alpha }}|\beta \rangle \right)}$$

Un ejemplo de superposición es el experimento de la doble rendija , en el que la superposición conduce a la interferencia cuántica . Otro ejemplo de la importancia de la fase relativa son las oscilaciones de Rabi , donde la fase relativa de dos estados varía en el tiempo debido a la ecuación de Schrödinger . La superposición resultante termina oscilando de ida y vuelta entre dos estados diferentes.

Un estado cuántico puro es un estado que puede describirse mediante un único vector ket, como se describió anteriormente. Un estado cuántico mixto es un conjunto estadístico de estados puros (véase mecánica estadística cuántica ). ^{[3] : 73}

Los estados mixtos surgen en mecánica cuántica en dos situaciones diferentes: primero, cuando no se conoce completamente la preparación del sistema y, por lo tanto, hay que tratar con un conjunto estadístico de preparaciones posibles; y segundo, cuando se quiere describir un sistema físico que está entrelazado con otro, ya que su estado no puede describirse mediante un estado puro. En el primer caso, teóricamente podría haber otra persona que conociera la historia completa del sistema y, por lo tanto, describiría el mismo sistema como un estado puro; en este caso, la matriz de densidad se utiliza simplemente para representar el conocimiento limitado de un estado cuántico. En el segundo caso, sin embargo, la existencia del entrelazamiento cuántico impide teóricamente la existencia de un conocimiento completo sobre el subsistema y es imposible para cualquier persona describir el subsistema de un par entrelazado como un estado puro.

Los estados mixtos surgen inevitablemente de los estados puros cuando, para un sistema cuántico compuesto con un estado entrelazado en él, la parte es inaccesible para el observador. ^{[3] : 121–122} El estado de la parte se expresa entonces como la traza parcial sobre .${\displaystyle H_{1}\otimes H_{2}}$${\displaystyle H_{2}}$${\displaystyle H_{1}}$${\displaystyle H_{2}}$

Un estado mixto no puede describirse con un único vector ket. ^{[21] : 691–692} En cambio, se describe mediante su matriz de densidad asociada (u operador de densidad ), generalmente denotada ρ . Las matrices de densidad pueden describir estados tanto mixtos como puros, tratándolos en el mismo pie de igualdad. Además, un estado cuántico mixto en un sistema cuántico dado descrito por un espacio de Hilbert siempre puede representarse como la traza parcial de un estado cuántico puro (llamado purificación ) en un sistema bipartito más grande para un espacio de Hilbert suficientemente grande .${\displaystyle H}$${\displaystyle H\otimes K}$${\displaystyle K}$

La matriz de densidad que describe un estado mixto se define como un operador de la forma donde p _s es la fracción del conjunto en cada estado puro. La matriz de densidad se puede considerar como una forma de utilizar el formalismo de una partícula para describir el comportamiento de muchas partículas similares al dar una distribución de probabilidad (o conjunto) de estados en los que se pueden encontrar estas partículas.$${\displaystyle \rho =\sum _{s}p_{s}|\psi _{s}\rangle \langle \psi _{s}|}$$${\displaystyle |\psi _{s}\rangle .}$

Un criterio simple para comprobar si una matriz de densidad describe un estado puro o mixto es que la traza de ρ ² sea igual a 1 si el estado es puro, y menor que 1 si el estado es mixto. ^{[d] [22]} Otro criterio equivalente es que la entropía de von Neumann sea 0 para un estado puro, y estrictamente positiva para un estado mixto.

Las reglas para la medición en mecánica cuántica son particularmente simples de enunciar en términos de matrices de densidad. Por ejemplo, el promedio del conjunto ( valor esperado ) de una medición correspondiente a un observable A está dado por donde y son kets propios y valores propios, respectivamente, para el operador A , y " tr " denota traza. ^{[3] : 73} Es importante notar que están ocurriendo dos tipos de promedio, uno (over ) siendo el valor esperado usual del observable cuando el quantum está en el estado , y el otro (over ) siendo un promedio estadístico (dicho incoherente ) con las probabilidades p _s de que el quantum esté en esos estados.$${\displaystyle \langle A\rangle =\sum _{s}p_{s}\langle \psi _{s}|A|\psi _{s}\rangle =\sum _{s}\sum _{i}p_{s}a_{i}|\langle \alpha _{i}|\psi _{s}\rangle |^{2}=\operatorname {tr} (\rho A)}$$${\displaystyle |\alpha _{i}\rangle }$${\displaystyle a_{i}}$${\displaystyle i}$${\displaystyle |\psi _{s}\rangle }$${\displaystyle s}$

Los estados se pueden formular en términos de observables, en lugar de como vectores en un espacio vectorial. Estos son funcionales lineales normalizados positivos en un álgebra C* o, a veces, otras clases de álgebras de observables. Consulte Estado en un álgebra C* y Construcción de Gelfand–Naimark–Segal para obtener más detalles.

El concepto de estados cuánticos, en particular el contenido de la sección Formalismo en física cuántica mencionada anteriormente, se trata en la mayoría de los libros de texto estándar sobre mecánica cuántica.

Para una discusión de los aspectos conceptuales y una comparación con los estados clásicos, véase:

• Isham, Chris J (1995). Lecciones sobre teoría cuántica: fundamentos matemáticos y estructurales . Imperial College Press . ISBN 978-1-86094-001-9.

Para una cobertura más detallada de los aspectos matemáticos, consulte:

• Bratteli, Ola ; Robinson, Derek W (1987). Álgebras de operadores y mecánica estadística cuántica 1 . Springer. ISBN 978-3-540-17093-8. 2da edición.En particular, véase la sección 2.3.

Para una discusión sobre las purificaciones de estados cuánticos mixtos, consulte el Capítulo 2 de las notas de clase de John Preskill para Física 219 en Caltech.

Para una discusión de los aspectos geométricos, véase:

• Bengtsson I; Życzkowski K (2006). Geometría de estados cuánticos . Cambridge: Cambridge University Press., segunda edición revisada (2017)