Historia de la mecánica cuántica

La historia de la mecánica cuántica es una parte fundamental de la historia de la física moderna . Los capítulos principales de esta historia comienzan con el surgimiento de las ideas cuánticas para explicar fenómenos individuales (radiación de cuerpo negro, efecto fotoeléctrico, espectros de emisión solar), una era llamada las teorías cuánticas antiguas o antiguas. ^[1] Basándose en la tecnología desarrollada en la mecánica clásica , la invención de la mecánica ondulatoria por Erwin Schrödinger y la expansión por muchos otros desencadenan la era "moderna" que comienza alrededor de 1925. El trabajo de teoría cuántica relativista de Paul Dirac lo llevó a explorar las teorías cuánticas de la radiación, que culminaron en la electrodinámica cuántica , la primera teoría cuántica de campos . La historia de la mecánica cuántica continúa en la historia de la teoría cuántica de campos . La historia de la química cuántica , la base teórica de la estructura química , la reactividad y el enlace , se entrelaza con los eventos discutidos en este artículo.

La frase "mecánica cuántica" fue acuñada (en alemán, Quantenmechanik ) por el grupo de físicos que incluía a Max Born, Werner Heisenberg y Wolfgang Pauli , en la Universidad de Göttingen a principios de la década de 1920, y se utilizó por primera vez en el artículo de Born de 1925 "Zur Quantenmechanik" . ^{[2] [3]}

La palabra quantum proviene del latín "cuánto" (al igual que cantidad ). Algo que está cuantizado , como la energía de los osciladores armónicos de Planck, solo puede tomar valores específicos. Por ejemplo, en la mayoría de los países, el dinero está efectivamente cuantizado, siendo el quantum de dinero la moneda de menor valor en circulación. La mecánica es la rama de la ciencia que estudia la acción de las fuerzas sobre los objetos. Por lo tanto, la mecánica cuántica es la parte de la mecánica que estudia los objetos para los que se cuantizan propiedades particulares.

Los descubrimientos del siglo XIX , tanto los éxitos como los fracasos, prepararon el escenario para el surgimiento de la mecánica cuántica.

A partir de 1670 y durante tres décadas, Isaac Newton desarrolló y defendió su teoría corpuscular , argumentando que las líneas perfectamente rectas de reflexión demostraban la naturaleza de partícula de la luz, ya que en ese momento ninguna teoría ondulatoria demostraba el viaje en línea recta. ^{[1] : 19} Explicó la refracción postulando que las partículas de luz se aceleraban lateralmente al entrar en un medio más denso. Casi al mismo tiempo, los contemporáneos de Newton, Robert Hooke y Christiaan Huygens , y más tarde Augustin-Jean Fresnel , refinaron matemáticamente el punto de vista ondulatorio, mostrando que si la luz viajaba a diferentes velocidades en diferentes medios, la refracción podía explicarse fácilmente como la propagación dependiente del medio de las ondas de luz. El principio de Huygens-Fresnel resultante fue extremadamente exitoso en reproducir el comportamiento de la luz y fue consistente con el descubrimiento de Thomas Young de la interferencia de ondas de la luz mediante su experimento de doble rendija en 1801. ^[4] La visión de las ondas no desplazó inmediatamente la visión de los rayos y las partículas, pero comenzó a dominar el pensamiento científico sobre la luz a mediados del siglo XIX, ya que podía explicar los fenómenos de polarización que las alternativas no podían. ^[5]

James Clerk Maxwell descubrió que podía aplicar las ecuaciones de Maxwell que había descubierto previamente , junto con una ligera modificación, para describir ondas autopropagantes de campos eléctricos y magnéticos oscilantes. Rápidamente se hizo evidente que la luz visible, la luz ultravioleta y la luz infrarroja eran ondas electromagnéticas de diferente frecuencia. ^{[1] : 272} Esta teoría se convirtió en un ingrediente fundamental en el comienzo de la mecánica cuántica.

A principios del siglo XIX, la investigación química de John Dalton y Amedeo Avogadro dio peso a la teoría atómica de la materia, una idea que James Clerk Maxwell , Ludwig Boltzmann y otros aprovecharon para establecer la teoría cinética de los gases . Los éxitos de la teoría cinética dieron más credibilidad a la idea de que la materia está compuesta de átomos, pero la teoría también tenía deficiencias que solo se resolverían con el desarrollo de la mecánica cuántica. ^[6] La existencia de átomos no fue aceptada universalmente entre los físicos o químicos; Ernst Mach , por ejemplo, era un acérrimo antiatomista. ^[7]

Los primeros indicios de problemas en la mecánica clásica se plantearon en relación con la dependencia de la temperatura de las propiedades de los gases. ^[8] Ludwig Boltzmann sugirió en 1877 que los niveles de energía de un sistema físico, como una molécula , podrían ser discretos (en lugar de continuos). La justificación de Boltzmann para la presencia de niveles de energía discretos en moléculas como las del gas yodo tuvo su origen en sus teorías de termodinámica estadística y mecánica estadística y fue respaldada por argumentos matemáticos , como también sería el caso veinte años después con la primera teoría cuántica propuesta por Max Planck.

A finales del siglo XIX, J. J. Thomson estableció que los electrones tienen una carga negativa opuesta pero del mismo tamaño que la de un ion de hidrógeno, pero con una masa mil veces menor. Se sabía que muchos de estos electrones estaban asociados a cada átomo. ^{[1] : 365}

A lo largo del siglo XIX, muchos estudios investigaron detalles en el espectro de intensidad versus frecuencia de la luz emitida por las llamas, por el Sol o por objetos al rojo vivo. ^{[1] : 367} La fórmula de Rydberg resumió de manera efectiva las líneas oscuras observadas en el espectro, pero no proporcionó ningún modelo físico para explicarlas. El espectro emitido por objetos al rojo vivo podría explicarse en longitudes de onda altas o bajas, pero las dos teorías diferían.

La mecánica cuántica se desarrolló en dos fases distintas. La primera fase, conocida como la antigua teoría cuántica , comenzó alrededor de 1900 con enfoques radicalmente nuevos para explicar fenómenos físicos que no eran comprendidos por la mecánica clásica del siglo XIX. ^[1]

La radiación térmica es la radiación electromagnética emitida desde la superficie de un objeto debido a la energía interna del mismo. Si un objeto se calienta lo suficiente, comienza a emitir luz en el extremo rojo del espectro visible , ya que se pone al rojo vivo.

Al calentarlo, el color cambia de rojo a amarillo, blanco y azul, ya que emite luz en longitudes de onda cada vez más cortas (frecuencias más altas). Un emisor perfecto es también un absorbente perfecto: cuando está frío, un objeto así parece perfectamente negro, porque absorbe toda la luz que incide sobre él y no emite ninguna. En consecuencia, un emisor térmico ideal se conoce como cuerpo negro , y la radiación que emite se llama radiación de cuerpo negro .

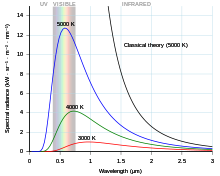
A finales del siglo XIX, la radiación térmica había sido bastante bien caracterizada experimentalmente. Se habían creado varias fórmulas que podían describir algunas de las mediciones experimentales de la radiación térmica: cómo la longitud de onda en la que la radiación es más fuerte cambia con la temperatura está dada por la ley de desplazamiento de Wien , la potencia total emitida por unidad de área está dada por la ley de Stefan-Boltzmann . La mejor explicación teórica de los resultados experimentales fue la ley de Rayleigh-Jeans, que concuerda bien con los resultados experimentales en longitudes de onda grandes (o, equivalentemente, frecuencias bajas), pero está muy en desacuerdo con longitudes de onda cortas (o frecuencias altas). De hecho, en longitudes de onda cortas, la física clásica predijo que un cuerpo caliente emitirá energía a un ritmo infinito. Este resultado, que es claramente erróneo, se conoce como la catástrofe ultravioleta . Sin embargo, la física clásica condujo a la ley de Rayleigh-Jeans , que, como se muestra en la figura, concuerda bien con los resultados experimentales en frecuencias bajas, pero está muy en desacuerdo con frecuencias altas. Los físicos buscaron una teoría única que explicara todos los resultados experimentales.

El primer modelo capaz de explicar el espectro completo de la radiación térmica fue propuesto por Max Planck en 1900. ^[9] Propuso un modelo matemático en el que la radiación térmica estaba en equilibrio con un conjunto de osciladores armónicos . Para reproducir los resultados experimentales, tuvo que suponer que cada oscilador emitía un número entero de unidades de energía en su única frecuencia característica, en lugar de poder emitir cualquier cantidad arbitraria de energía. En otras palabras, la energía emitida por un oscilador estaba cuantizada . El cuanto de energía de cada oscilador, según Planck, era proporcional a la frecuencia del oscilador; la constante de proporcionalidad se conoce ahora como la constante de Planck .

La ley de Planck fue la primera teoría cuántica de la física, y Planck ganó el Premio Nobel en 1918 "en reconocimiento a los servicios que prestó al avance de la física con su descubrimiento de los cuantos de energía". ^[10] Sin embargo, en ese momento, la opinión de Planck era que la cuantización era puramente una construcción matemática heurística , en lugar de (como se cree ahora) un cambio fundamental en nuestra comprensión del mundo. ^[11]

En 1887, Heinrich Hertz observó que cuando la luz con suficiente frecuencia incide sobre una superficie metálica, ésta emite rayos catódicos . ^{[1] : I:362} Diez años después, JJ Thomson demostró que los numerosos informes sobre rayos catódicos eran en realidad "corpúsculos" y rápidamente se los empezó a llamar electrones . En 1902, Philipp Lenard descubrió que la máxima energía posible de un electrón expulsado no está relacionada con su intensidad . ^[12] Esta observación está en desacuerdo con el electromagnetismo clásico, que predice que la energía del electrón debería ser proporcional a la intensidad de la radiación incidente. ^{[13] : 24}

En 1905, Albert Einstein sugirió que, si bien los modelos continuos de la luz funcionaban muy bien para los fenómenos ópticos promediados en el tiempo, para las transiciones instantáneas la energía de la luz puede producirse en un número finito de cuantos de energía. ^[14] En la sección de introducción de su artículo cuántico de marzo de 1905 "Desde un punto de vista heurístico sobre la emisión y transformación de la luz", Einstein afirma:

Según el supuesto que aquí se contempla, cuando un rayo de luz se propaga desde un punto, la energía no se distribuye de forma continua en espacios cada vez mayores, sino que consiste en un número finito de "cuantos de energía" que se localizan en puntos del espacio, se mueven sin dividirse y pueden ser absorbidos o generados sólo como un todo.

Esta afirmación ha sido calificada como la frase más revolucionaria escrita por un físico del siglo XX. ^[15] La energía de un solo cuanto de luz de frecuencia viene dada por la frecuencia multiplicada por la constante de Planck :${\estilo de visualización f}$${\estilo de visualización h}$

${\displaystyle E=hf}$

Einstein supuso que un cuanto de luz transfiere toda su energía a un solo electrón, impartiéndole como máximo una energía hf . Por lo tanto, sólo la frecuencia de la luz determina la energía máxima que se puede impartir al electrón; la intensidad de la fotoemisión es proporcional a la intensidad del haz de luz. ^[14]

Einstein argumentó que se necesita una cierta cantidad de energía, llamada función de trabajo y denotada por φ , para extraer un electrón del metal. ^[16] Esta cantidad de energía es diferente para cada metal. Si la energía de los cuantos de luz es menor que la función de trabajo, entonces no transporta suficiente energía para extraer el electrón del metal. La frecuencia umbral, f ₀ , es la frecuencia de un cuanto de luz cuya energía es igual a la función de trabajo:

${\displaystyle \varphi =hf_{0}.}$

Si f es mayor que f ₀ , la energía hf es suficiente para arrancar un electrón. El electrón expulsado tiene una energía cinética , E _k , que es, como máximo, igual a la energía de la luz menos la energía necesaria para desalojar al electrón del metal:

${\displaystyle E_{\text{k}}=hf-\varphi =h(f-f_{0}).}$

La descripción de Einstein de la luz como compuesta de cuantos de energía amplió la noción de Planck de energía cuantizada, que es que un solo cuanto de una frecuencia dada, f , proporciona una cantidad invariable de energía, hf . En la naturaleza, rara vez se encuentran cuantos individuales. El Sol y las fuentes de emisión disponibles en el siglo XIX emiten una enorme cantidad de energía cada segundo. La constante de Planck , h , es tan pequeña que la cantidad de energía en cada cuanto, hf es muy, muy pequeña. La luz que vemos incluye muchos billones de tales cuantos.

A principios del siglo XX, las pruebas exigían un modelo del átomo con una nube difusa de electrones con carga negativa que rodeaba un núcleo pequeño, denso y con carga positiva . Estas propiedades sugerían un modelo en el que los electrones giraban alrededor del núcleo como planetas en órbita alrededor de una estrella. El modelo clásico del átomo se denomina modelo planetario o, a veces, modelo de Rutherford , en honor a Ernest Rutherford , quien lo propuso en 1911, basándose en el experimento de la lámina de oro de Geiger-Marsden , que demostró por primera vez la existencia del núcleo. Sin embargo, también se sabía que el átomo en este modelo sería inestable: según la teoría clásica, los electrones en órbita están experimentando una aceleración centrípeta y, por lo tanto, deberían emitir radiación electromagnética; la pérdida de energía también hace que se desplacen en espiral hacia el núcleo, chocando con él en una fracción de segundo.

Un segundo enigma relacionado con esto era el espectro de emisión de los átomos. Cuando un gas se calienta, emite luz sólo en frecuencias discretas. Por ejemplo, la luz visible emitida por el hidrógeno consta de cuatro colores diferentes, como se muestra en la imagen siguiente. La intensidad de la luz a diferentes frecuencias también es diferente. En cambio, la luz blanca consiste en una emisión continua en todo el rango de frecuencias visibles. A finales del siglo XIX, una sencilla regla conocida como la fórmula de Balmer mostraba cómo se relacionaban entre sí las frecuencias de las diferentes líneas, aunque sin explicar por qué o hacer ninguna predicción sobre las intensidades. La fórmula también predecía algunas líneas espectrales adicionales en la luz ultravioleta e infrarroja que no se habían observado en ese momento. Estas líneas se observaron posteriormente de forma experimental, lo que aumentó la confianza en el valor de la fórmula.

Espectro de emisión del hidrógeno . Cuando se excita, el gas hidrógeno emite luz en cuatro colores distintos (líneas espectrales) en el espectro visible, así como una serie de líneas en el infrarrojo y el ultravioleta.

En 1905, Albert Einstein utilizó la teoría cinética para explicar el movimiento browniano . El físico francés Jean Baptiste Perrin utilizó el modelo del artículo de Einstein para determinar experimentalmente la masa y las dimensiones de los átomos, lo que permitió verificar empíricamente de forma directa la teoría atómica. ^{[ cita requerida ]}

En 1913, Niels Bohr propuso un nuevo modelo del átomo que incluía órbitas electrónicas cuantizadas: los electrones siguen orbitando el núcleo de forma muy similar a como lo hacen los planetas alrededor del Sol, pero se les permite habitar solo ciertas órbitas, no orbitar a una distancia arbitraria. ^[18] Cuando un átomo emitía (o absorbía) energía, el electrón no se movía en una trayectoria continua de una órbita alrededor del núcleo a otra, como podría esperarse clásicamente. En cambio, el electrón saltaba instantáneamente de una órbita a otra, emitiendo la luz emitida en forma de fotón. ^[19] Las posibles energías de los fotones emitidos por cada elemento estaban determinadas por las diferencias de energía entre las órbitas, por lo que el espectro de emisión de cada elemento contendría una serie de líneas. ^[20]

Partiendo de una simple suposición sobre la regla que deben respetar las órbitas, el modelo de Bohr fue capaz de relacionar las líneas espectrales observadas en el espectro de emisión del hidrógeno con constantes previamente conocidas. En el modelo de Bohr, no se permitía que el electrón emitiera energía de forma continua y chocara contra el núcleo: una vez que se encontraba en la órbita más cercana permitida, era estable para siempre. El modelo de Bohr no explicaba por qué las órbitas debían cuantificarse de esa manera, ni era capaz de hacer predicciones precisas para átomos con más de un electrón, ni de explicar por qué algunas líneas espectrales son más brillantes que otras.

Algunas suposiciones fundamentales del modelo de Bohr pronto resultaron erróneas, pero el resultado clave de que las líneas discretas en los espectros de emisión se deben a que alguna propiedad de los electrones de los átomos está cuantizada es correcto. La forma en que los electrones se comportan en realidad es sorprendentemente diferente del átomo de Bohr y de lo que vemos en el mundo de nuestra experiencia cotidiana; este modelo mecánico cuántico moderno del átomo se analiza a continuación.

Un paso importante se dio en la evolución de la teoría cuántica en el primer Congreso Solvay de 1911. Allí los físicos más destacados de la comunidad científica se reunieron para discutir el problema de la "Radiación y los Cuantos". Para entonces, se había publicado el modelo del átomo de Ernest Rutherford, ^{[21] [22]} pero gran parte de la discusión que involucraba la estructura atómica giraba en torno al modelo cuántico de Arthur Haas en 1910. Además, en el Congreso Solvay de 1911, Hendrik Lorentz sugirió después de la charla de Einstein sobre la estructura cuántica que la energía de un rotador se estableciera igual a nhv. ^{[23] [24] : 244} Esto fue seguido por otros modelos cuánticos como el modelo de John William Nicholson de 1912 que era nuclear y de momento angular discretizado. ^{[25] [26] [27]} Nicholson había introducido los espectros en su modelo atómico utilizando las oscilaciones de los electrones en un átomo nuclear perpendicular al plano orbital, manteniendo así la estabilidad. Los espectros atómicos de Nicholson identificaron muchas líneas no atribuidas en los espectros solares y nebulares. ^{[25] [28] [29] [24] : 278}

En 1913, Bohr explicó las líneas espectrales del átomo de hidrógeno , nuevamente mediante el uso de la cuantización, en su artículo de julio de 1913 Sobre la constitución de átomos y moléculas en el que discutió y citó el modelo de Nicholson. ^{[30] [31] [27]} En el modelo de Bohr , el átomo de hidrógeno se representa como un núcleo pesado, cargado positivamente, orbitado por un electrón ligero, cargado negativamente. El electrón solo puede existir en ciertas órbitas discretamente separadas, etiquetadas por su momento angular , que está restringido a ser un múltiplo entero de la constante de Planck reducida . El éxito clave del modelo residió en explicar la fórmula de Rydberg para las líneas espectrales de emisión del hidrógeno atómico mediante el uso de las transiciones de electrones entre órbitas. ^{[24] : 276} Si bien la fórmula de Rydberg se conocía experimentalmente, no obtuvo una base teórica hasta que se introdujo el modelo de Bohr. El modelo de Bohr no sólo explicó las razones de la estructura de la fórmula de Rydberg, sino que también proporcionó una justificación de las constantes físicas fundamentales que conforman los resultados empíricos de la fórmula.

Además, la aplicación de la teoría cuántica de Planck al electrón permitió a Stefan Procopiu en 1911-1913, y posteriormente a Niels Bohr en 1913, calcular el momento magnético del electrón , que más tarde se llamó " magnetón "; cálculos cuánticos similares, pero con valores numéricamente bastante diferentes, fueron posibles posteriormente tanto para los momentos magnéticos del protón como del neutrón , que son tres órdenes de magnitud más pequeños que el del electrón.

Estas teorías, aunque exitosas, eran estrictamente fenomenológicas : durante ese tiempo, no había una justificación rigurosa para la cuantificación , aparte, tal vez, de la discusión de Henri Poincaré sobre la teoría de Planck en su artículo de 1912 Sur la théorie des quanta . ^{[32] [33]} Se las conoce colectivamente como la antigua teoría cuántica .

La cuantificación del momento angular orbital del electrón combinada con el momento magnético del electrón sugirió que los átomos con un momento magnético deberían mostrar un comportamiento cuantificado en un campo magnético. En 1922, Otto Stern y Walther Gerlach se propusieron probar esta teoría. Calentaron plata en un tubo de vacío equipado con una serie de ranuras estrechas alineadas, creando un haz molecular de átomos de plata. Dispararon este haz a través de un campo magnético no homogéneo . En lugar de un patrón continuo de átomos de plata, encontraron dos haces. ^[34]

En mecánica clásica, un imán lanzado a través de un campo magnético puede desviarse una distancia pequeña o grande hacia arriba o hacia abajo en relación con su polo norte, apuntando hacia arriba, hacia abajo o en algún punto intermedio. Los átomos que Stern y Gerlach lanzaron a través del campo magnético actuaron de manera similar. Sin embargo, mientras que los imanes podían desviarse distancias variables, los átomos siempre serían desviados una distancia constante hacia arriba o hacia abajo. Esto implicaba que la propiedad del átomo que corresponde a la orientación del imán debe ser cuantificada, tomando uno de dos valores (hacia arriba o hacia abajo), en lugar de elegirse libremente desde cualquier ángulo.

La elección de la orientación del campo magnético utilizado en el experimento de Stern-Gerlach es arbitraria. En la animación que se muestra aquí, el campo es vertical y, por lo tanto, los átomos se desvían hacia arriba o hacia abajo. Si se gira el imán un cuarto de vuelta, los átomos se desvían hacia la izquierda o hacia la derecha. El uso de un campo vertical muestra que el espín a lo largo del eje vertical está cuantizado, y el uso de un campo horizontal muestra que el espín a lo largo del eje horizontal está cuantizado.

Los resultados del experimento de Stern-Gerlach causaron sensación, sobre todo porque científicos de primera línea, entre ellos Einstein y Paul Ehrenfest, argumentaron que los átomos de plata deberían tener orientaciones aleatorias en las condiciones del experimento: la cuantificación no debería haber sido observable. ^[34] Pasarían al menos cinco años antes de que se resolviera este misterio: se observó cuantificación, pero no se debió al momento angular orbital.

En 1925, Ralph Kronig propuso que los electrones se comportan como si giraran sobre sí mismos, o "giraran", alrededor de un eje. ^{[35] : 56} El espín generaría un pequeño momento magnético que dividiría los niveles de energía responsables de las líneas espectrales, de acuerdo con las mediciones existentes. Dos electrones en el mismo orbital ocuparían estados cuánticos distintos si "giraran" en direcciones opuestas, satisfaciendo así el principio de exclusión . Desafortunadamente, la teoría tenía dos fallas significativas: dos valores calculados por Kronig estaban desfasados ​​por un factor de dos. Los colegas superiores de Kronig desalentaron su trabajo y nunca se publicó.

Diez meses después, los físicos holandeses George Uhlenbeck y Samuel Goudsmit de la Universidad de Leiden publicaron su teoría de la autorrotación de los electrones. ^[36] El modelo, como el de Kronig, era esencialmente clásico pero dio lugar a una predicción cuántica.

En 1924 Louis de Broglie publicó una hipótesis innovadora: la materia tiene propiedades ondulatorias. Basándose en la propuesta de Einstein de que el efecto fotoeléctrico puede describirse utilizando transferencias de energía cuantizadas y en la propuesta independiente de Einstein, de la relatividad especial, de que la masa en reposo es equivalente a la energía mediante , de Broglie propuso que la materia en movimiento parece tener una onda asociada con una longitud de onda donde es el momento de la materia a partir del movimiento. ^{[37] [38]} Al exigir que su longitud de onda rodee un átomo, explicó la cuantización de las órbitas de Bohr. ^{[1] : 217} Simultáneamente, esto demostró que el comportamiento ondulatorio de la luz era esencialmente un efecto cuántico. ^{[1] : 216}$Estilo de visualización E=m_{0}c^{2}}$${\displaystyle \lambda = h/p}$${\estilo de visualización p}$

De Broglie amplió el modelo de Bohr del átomo al demostrar que un electrón en órbita alrededor de un núcleo podría considerarse como poseedor de propiedades ondulatorias. En particular, un electrón se observa solo en situaciones que permiten una onda estacionaria alrededor de un núcleo . Un ejemplo de una onda estacionaria es una cuerda de violín, que está fija en ambos extremos y se puede hacer vibrar. Las ondas creadas por un instrumento de cuerda parecen oscilar en su lugar, moviéndose de cresta a valle en un movimiento de arriba a abajo. La longitud de onda de una onda estacionaria está relacionada con la longitud del objeto vibrante y las condiciones de contorno. Por ejemplo, debido a que la cuerda del violín está fija en ambos extremos, puede transportar ondas estacionarias de longitudes de onda , donde l es la longitud y n es un entero positivo. De Broglie sugirió que las órbitas permitidas para los electrones eran aquellas para las cuales la circunferencia de la órbita sería un número entero de longitudes de onda. La longitud de onda del electrón, por lo tanto, determina que solo sean posibles las órbitas de Bohr a ciertas distancias del núcleo. A su vez, a cualquier distancia del núcleo menor que un cierto valor, sería imposible establecer una órbita. La distancia mínima posible al núcleo se denomina radio de Bohr. ^[39] El tratamiento que De Broglie hizo del átomo de Bohr no tuvo éxito, pero su hipótesis sirvió como punto de partida para la ecuación de onda de Schrödinger.${\textstyle {\frac {2l}{n}}}$

La materia comportándose como una onda fue demostrada experimentalmente por primera vez para los electrones: un haz de electrones puede exhibir difracción , al igual que un haz de luz o una onda de agua. Tres años después de que de Broglie publicara su hipótesis, dos grupos diferentes demostraron la difracción de electrones. En la Universidad de Aberdeen , George Paget Thomson y Alexander Reid pasaron un haz de electrones a través de una fina película de celuloide, luego películas de metal, y observaron los patrones de interferencia predichos. (Alexander Reid, que era estudiante de posgrado de Thomson, realizó los primeros experimentos, pero murió poco después en un accidente de motocicleta ^[40] y rara vez se lo menciona). En Bell Labs , Clinton Joseph Davisson y Lester Halbert Germer reflejaron un haz de electrones de una muestra de níquel en su experimento, observando haces bien definidos predichos por modelos de ondas que regresaban del cristal. ^{[1] : II:218} De Broglie fue galardonado con el Premio Nobel de Física en 1929 por su hipótesis; Thomson y Davisson compartieron el Premio Nobel de Física en 1937 por su trabajo experimental.

Basándose en el planteamiento de De Broglie, la mecánica cuántica moderna nació en 1925, cuando los físicos alemanes Werner Heisenberg, Max Born y Pascual Jordan ^{[41] [42]} desarrollaron la mecánica matricial y el físico austríaco Erwin Schrödinger inventó la mecánica ondulatoria y la ecuación de Schrödinger no relativista como aproximación del caso generalizado de la teoría de De Broglie. ^[43] Posteriormente, Schrödinger demostró que los dos planteamientos eran equivalentes. Las primeras aplicaciones de la mecánica cuántica a los sistemas físicos fueron la determinación algebraica del espectro del hidrógeno por Wolfgang Pauli ^[44] y el tratamiento de las moléculas diatómicas por Lucy Mensing . ^[45]

El fin de la primera era de la mecánica cuántica se produjo con la publicación por parte de De Broglie de su hipótesis de las ondas de materia , ^{[1] : 268,} que condujo al descubrimiento de Schrödinger de la mecánica ondulatoria para la materia. Las predicciones precisas del espectro de absorción del hidrógeno aseguraron una amplia aceptación de la nueva teoría cuántica. ^{[1] : 275}

En 1925, Werner Heisenberg intentó resolver uno de los problemas que el modelo de Bohr dejaba sin respuesta, explicando las intensidades de las diferentes líneas en el espectro de emisión del hidrógeno. Mediante una serie de analogías matemáticas, escribió el análogo mecánico-cuántico para el cálculo clásico de intensidades. ^[46] Poco después, el colega de Heisenberg, Max Born, se dio cuenta de que el método de Heisenberg para calcular las probabilidades de las transiciones entre los diferentes niveles de energía podía expresarse mejor utilizando el concepto matemático de matrices .

Heisenberg formuló una versión temprana del principio de incertidumbre en 1927, analizando un experimento mental en el que se intenta medir simultáneamente la posición y el momento de un electrón . Sin embargo, Heisenberg no dio definiciones matemáticas precisas de lo que significaba la "incertidumbre" en estas mediciones, un paso que darían poco después Earle Hesse Kennard , Wolfgang Pauli y Hermann Weyl . ^{[47] [48]}

En la primera mitad de 1926, basándose en la hipótesis de De Broglie, Erwin Schrödinger desarrolló la ecuación que describe el comportamiento de una onda mecánico-cuántica. ^[49] El modelo matemático, llamado ecuación de Schrödinger en honor a su creador, es fundamental para la mecánica cuántica, define los estados estacionarios permitidos de un sistema cuántico y describe cómo cambia el estado cuántico de un sistema físico en el tiempo. ^[50] La onda en sí se describe mediante una función matemática conocida como " función de onda ". Schrödinger dijo que la función de onda proporciona los "medios para predecir la probabilidad de los resultados de la medición". ^[51]

Schrödinger fue capaz de calcular los niveles de energía del hidrógeno al tratar el electrón de un átomo de hidrógeno como una onda clásica, que se mueve en un pozo de potencial eléctrico creado por el protón. Este cálculo reprodujo con precisión los niveles de energía del modelo de Bohr.

En mayo de 1926, Schrödinger demostró que la mecánica matricial de Heisenberg y su propia mecánica ondulatoria hacían las mismas predicciones sobre las propiedades y el comportamiento del electrón; matemáticamente, las dos teorías tenían una forma subyacente común. Sin embargo, los dos hombres discrepaban sobre la interpretación de su teoría mutua. Por ejemplo, Heisenberg aceptó la predicción teórica de saltos de electrones entre orbitales en un átomo, ^[52] pero Schrödinger esperaba que una teoría basada en propiedades continuas de tipo ondulatorio pudiera evitar lo que él llamó (parafraseado por Wilhelm Wien ) "esta tontería sobre los saltos cuánticos". ^[53] Al final, el enfoque de Heisenberg ganó y los saltos cuánticos se confirmaron. ^[54]

Bohr, Heisenberg y otros intentaron explicar lo que significan realmente estos resultados experimentales y modelos matemáticos. El término interpretación de Copenhague se ha aplicado a sus puntos de vista en retrospectiva, pasando por alto las diferencias entre ellos. ^{[55] [56] [57] [58] [59] [60]} Si bien no existe una declaración definitiva de "la" interpretación de Copenhague, las siguientes ideas se consideran ampliamente como características de ella.

1. Un sistema está completamente descrito por un estado cuántico (Heisenberg)
2. La forma en que el estado cuántico cambia a lo largo del tiempo está dada por una ecuación de onda: la ecuación de Schrödinger, que imparte características de onda a la luz y a la materia.
3. Las interacciones atómicas son discontinuas (Planck las denominó " cuanto de acción ").
4. La descripción de la naturaleza es esencialmente probabilística. La probabilidad de un evento (por ejemplo, la aparición de una partícula en la pantalla en el experimento de la doble rendija) está relacionada con el cuadrado del valor absoluto de la amplitud de su función de onda. ( Regla de Born , de Max Born , que da un significado físico a la función de onda en la interpretación de Copenhague: la amplitud de probabilidad )
5. Los valores de pares incompatibles de propiedades del sistema no pueden conocerse al mismo tiempo. ( Principio de incertidumbre de Heisenberg )
6. La materia, al igual que la luz, presenta una dualidad onda-partícula. Un experimento puede demostrar las propiedades de la materia como partículas o como ondas, pero no ambas al mismo tiempo. ( Principio de complementariedad de Bohr ^[61] )
7. Los dispositivos de medición son esencialmente dispositivos clásicos y miden propiedades clásicas como la posición y el momento.
8. La descripción mecánica cuántica de los grandes sistemas debería aproximarse mucho a la descripción clásica ( principio de correspondencia de Bohr y Heisenberg) .

El modelo atómico de Bohr era esencialmente planetario, con los electrones orbitando alrededor del "sol" nuclear. Sin embargo, el principio de incertidumbre establece que un electrón no puede tener simultáneamente una ubicación exacta y una velocidad como la tiene un planeta. En lugar de órbitas clásicas, se dice que los electrones habitan orbitales atómicos . Un orbital es la "nube" de posibles ubicaciones en las que podría encontrarse un electrón, una distribución de probabilidades en lugar de una ubicación precisa. ^[62] Cada orbital es tridimensional, en lugar de la órbita bidimensional, y a menudo se representa como una región tridimensional dentro de la cual hay un 95 por ciento de probabilidad de encontrar el electrón. ^[63]

Schrödinger fue capaz de calcular los niveles de energía del hidrógeno al tratar el electrón de un átomo de hidrógeno como una onda, representada por la " función de onda " Ψ , en un pozo de potencial eléctrico , V , creado por el protón. Las soluciones de la ecuación de Schrödinger ^{[ aclaración necesaria ]} son ​​distribuciones de probabilidades para las posiciones y ubicaciones de los electrones. Los orbitales tienen una gama de formas diferentes en tres dimensiones. Las energías de los diferentes orbitales se pueden calcular y coinciden con precisión con los niveles de energía del modelo de Bohr.

Dentro de la imagen de Schrödinger, cada electrón tiene cuatro propiedades:

1. Una designación "orbital", que indica si la partícula-onda es la que está más cerca del núcleo con menos energía o una que está más lejos del núcleo con más energía;
2. La "forma" de la órbita, esférica o de otro tipo;
3. La "inclinación" del orbital, que determina el momento magnético del orbital alrededor del eje z .
4. El "spin" del electrón.

El nombre colectivo de estas propiedades es el estado cuántico del electrón. El estado cuántico se puede describir asignando un número a cada una de estas propiedades; estos se conocen como los números cuánticos del electrón . El estado cuántico del electrón se describe mediante su función de onda. El principio de exclusión de Pauli exige que no haya dos electrones dentro de un átomo que tengan los mismos valores de los cuatro números.

La primera propiedad que describe el orbital es el número cuántico principal , n , que es el mismo que en el modelo de Bohr. n denota el nivel de energía de cada orbital. Los valores posibles para n son números enteros:

${\displaystyle n=1,2,3\lpuntos}$

El siguiente número cuántico, el número cuántico azimutal , denominado l , describe la forma del orbital. La forma es una consecuencia del momento angular del orbital. El momento angular representa la resistencia de un objeto giratorio a acelerar o desacelerar bajo la influencia de una fuerza externa. El número cuántico azimutal representa el momento angular orbital de un electrón alrededor de su núcleo. Los valores posibles para l son números enteros de 0 a n − 1 (donde n es el número cuántico principal del electrón):

${\displaystyle l=0,1,\lpuntos ,n-1.}$

La forma de cada orbital se suele indicar con una letra, en lugar de con su número cuántico azimutal. La primera forma ( l = 0) se denota con la letra s (una regla mnemotécnica que es " esfera "). La siguiente forma se denota con la letra p y tiene la forma de una mancuerna. Los otros orbitales tienen formas más complicadas (véase orbital atómico ) y se denotan con las letras d , f , g , etc.

El tercer número cuántico, el número cuántico magnético , describe el momento magnético del electrón y se denota por m _l (o simplemente m ). Los valores posibles para m _l son números enteros desde − l hasta l (donde l es el número cuántico azimutal del electrón):

${\displaystyle m_{l}=-l,-(l-1),\ldots ,0,\ldots ,(l-1),l.}$

El número cuántico magnético mide el componente del momento angular en una dirección determinada. La elección de la dirección es arbitraria; convencionalmente se elige la dirección z.

El cuarto número cuántico, el número cuántico de espín (relativo a la "orientación" del espín del electrón) se denota m _s , con valores + 1 ⁄ 2 o − 1 ⁄ 2 .

El químico Linus Pauling escribió, a modo de ejemplo:

En el caso de un átomo de helio con dos electrones en el orbital 1 s , el principio de exclusión de Pauli requiere que los dos electrones difieran en el valor de un número cuántico. Sus valores de n , l y m _l son los mismos. En consecuencia, deben diferir en el valor de m _s , que puede tener el valor de + 1 ⁄ 2 para un electrón y − 1 ⁄ 2 para el otro. ^[62]

La estructura y la simetría subyacentes de los orbitales atómicos y la forma en que los electrones los llenan son las que dan origen a la organización de la tabla periódica . La forma en que los orbitales atómicos de los diferentes átomos se combinan para formar orbitales moleculares determina la estructura y la fuerza de los enlaces químicos entre los átomos.

El campo de la química cuántica fue iniciado por los físicos Walter Heitler y Fritz London , quienes publicaron un estudio del enlace covalente de la molécula de hidrógeno en 1927. La química cuántica fue desarrollada posteriormente por un gran número de trabajadores, incluido el químico teórico estadounidense Linus Pauling en Caltech , y John C. Slater en varias teorías como la teoría de orbitales moleculares o la teoría de valencia.

A partir de 1927, Paul Dirac inició el proceso de unificación de la mecánica cuántica con la relatividad especial al proponer la ecuación de Dirac para el electrón. La ecuación de Dirac logra la descripción relativista de la función de onda de un electrón que Schrödinger no pudo obtener. Predice el espín del electrón y llevó a Dirac a predecir la existencia del positrón . También fue pionero en el uso de la teoría de operadores, incluida la influyente notación bra-ket , como se describe en su famoso libro de texto de 1930. Durante el mismo período, el polímata húngaro John von Neumann formuló la base matemática rigurosa de la mecánica cuántica como la teoría de operadores lineales en espacios de Hilbert, como se describe en su también famoso libro de texto de 1932. Estos, como muchos otros trabajos del período fundacional, todavía se mantienen y siguen utilizándose ampliamente.

A partir de 1927, los investigadores intentaron aplicar la mecánica cuántica a campos en lugar de partículas individuales, lo que dio como resultado las teorías cuánticas de campos. Los primeros trabajadores en esta área incluyen a PAM Dirac , W. Pauli, V. Weisskopf y P. Jordan . Esta área de investigación culminó en la formulación de la electrodinámica cuántica por RP Feynman , F. Dyson , J. Schwinger y S. Tomonaga durante la década de 1940. La electrodinámica cuántica describe una teoría cuántica de electrones, positrones y el campo electromagnético , y sirvió como modelo para las teorías cuánticas de campos posteriores . ^{[41] [42] [64]}

La teoría de la cromodinámica cuántica se formuló a principios de la década de 1960. La teoría tal como la conocemos hoy fue formulada por Politzer , Gross y Wilczek en 1975.

Basándose en el trabajo pionero de Schwinger , Higgs y Goldstone , los físicos Glashow , Weinberg y Salam demostraron independientemente cómo la fuerza nuclear débil y la electrodinámica cuántica podían fusionarse en una única fuerza electrodébil , por lo que recibieron el Premio Nobel de Física en 1979.

La ciencia de la información cuántica se desarrolló en las últimas décadas del siglo XX, comenzando con resultados teóricos como el teorema de Holevo , el concepto de medidas generalizadas o POVM , la propuesta de distribución de claves cuánticas de Bennett y Brassard y el algoritmo de Shor .

• Experimento de doble rendija de Thomas Young que demuestra la naturaleza ondulatoria de la luz. (c. 1801)
• Henri Becquerel descubre la radiactividad (1896)
• Experimentos con el tubo de rayos catódicos de J. J. Thomson (descubre el electrón y su carga negativa). (1897)
• El estudio de la radiación del cuerpo negro entre 1850 y 1900, que no podría explicarse sin conceptos cuánticos.
• El efecto fotoeléctrico : Einstein lo explicó en 1905 (y más tarde recibió un premio Nobel por ello) utilizando el concepto de fotones, partículas de luz con energía cuantificada.
• Experimento de la gota de aceite de Robert Millikan , que demostró que la carga eléctrica se presenta en cuantos (unidades enteras). (1909)
• El experimento de la lámina de oro de Ernest Rutherford desmintió el modelo atómico del budín de pasas , que sugería que la masa y la carga positiva del átomo se distribuyen de manera casi uniforme, lo que condujo al modelo planetario del átomo (1911).
• El experimento de colisión de electrones de James Franck y Gustav Hertz muestra que la absorción de energía por los átomos de mercurio está cuantizada. (1914)
• Otto Stern y Walther Gerlach realizan el experimento de Stern-Gerlach , que demuestra la naturaleza cuantizada del espín de las partículas . (1920)
• Arthur Compton con el experimento de dispersión Compton (1923)
• Clinton Davisson y Lester Germer demuestran la naturaleza ondulatoria del electrón ^[65] en el experimento de difracción de electrones . (1927)
• Carl David Anderson con el descubrimiento del positrón (1932), validó la predicción teórica de Paul Dirac sobre esta partícula (1928)
• El experimento de Lamb - Retherford descubrió el desplazamiento de Lamb (1947), que condujo al desarrollo de la electrodinámica cuántica.
• Clyde L. Cowan y Frederick Reines confirman la existencia del neutrino en el experimento del neutrino (1955)
• Experimento de doble rendija con electrones de Claus Jönsson (1961)
• El efecto Hall cuántico , descubierto en 1980 por Klaus von Klitzing , ha permitido definir un nuevo estándar práctico para la resistencia eléctrica y determinar de forma extremadamente precisa e independiente la constante de estructura fina .
• La verificación experimental del entrelazamiento cuántico por John Clauser y Stuart Freedman (1972)
• El experimento del interferómetro Mach-Zehnder realizado por Paul Kwiat , Harold Wienfurter, Thomas Herzog, Anton Zeilinger y Mark Kasevich, que proporcionó una verificación experimental del probador de bombas Elitzur-Vaidman , demostró que es posible realizar mediciones sin interacción . (1994)

• Bacciagaluppi, Guido; Valentini, Antony (2009), La teoría cuántica en la encrucijada: reconsiderando la conferencia Solvay de 1927 , Cambridge, Reino Unido: Cambridge University Press, p. 9184, arXiv : quant-ph/0609184 , Bibcode :2006quant.ph..9184B, ISBN 978-0-521-81421-8, OCLC  227191829
• Bernstein, Jeremy (2009), Saltos cuánticos, Cambridge, Massachusetts: Belknap Press de Harvard University Press, ISBN 978-0-674-03541-6
• Greenberger, Daniel, Hentschel, Klaus , Weinert, Friedel (Eds.) Compendio de física cuántica. Conceptos, experimentos, historia y filosofía , Nueva York: Springer, 2009. ISBN 978-3-540-70626-7 . 
• Jammer, Max (1966), El desarrollo conceptual de la mecánica cuántica , Nueva York: McGraw-Hill, OCLC  534562
• Jammer, Max (1974), La filosofía de la mecánica cuántica: Las interpretaciones de la mecánica cuántica en perspectiva histórica , Nueva York: Wiley, ISBN 0-471-43958-4, OCLC  969760
• A. Whitaker. La nueva era cuántica: del teorema de Bell a la computación cuántica y la teletransportación , Oxford University Press, 2011, ISBN 978-0-19-958913-5 
• Stephen Hawking. Los sueños de los que están hechas las cosas , Running Press, 2011, ISBN 978-0-76-243434-3 
• A. Douglas Stone. Einstein y el cuanto: la búsqueda del valiente suabo , Princeton University Press, 2006.

Wikiquote tiene citas relacionadas con Historia de la mecánica cuántica .