Teorema de Bell

El teorema de Bell es un término que engloba una serie de resultados estrechamente relacionados en física , todos los cuales determinan que la mecánica cuántica es incompatible con las teorías locales de variables ocultas , dadas algunas suposiciones básicas sobre la naturaleza de la medición. "Local" aquí se refiere al principio de localidad , la idea de que una partícula solo puede ser influenciada por su entorno inmediato, y que las interacciones mediadas por campos físicos no pueden propagarse más rápido que la velocidad de la luz . Las " variables ocultas " son supuestas propiedades de las partículas cuánticas que no están incluidas en la teoría cuántica pero que, sin embargo, afectan el resultado de los experimentos. En palabras del físico John Stewart Bell , por quien se nombra esta familia de resultados, "Si [una teoría de variables ocultas] es local, no estará de acuerdo con la mecánica cuántica, y si está de acuerdo con la mecánica cuántica, no será local". ^[1]

El primer resultado de este tipo fue presentado por Bell en 1964, basándose en la paradoja de Einstein-Podolsky-Rosen , que había llamado la atención sobre el fenómeno del entrelazamiento cuántico . Bell dedujo que si las mediciones se realizan de forma independiente en las dos partículas separadas de un par entrelazado, entonces la suposición de que los resultados dependen de variables ocultas dentro de cada mitad implica una restricción matemática sobre cómo se correlacionan los resultados de las dos mediciones. Dicha restricción se llamaría posteriormente desigualdad de Bell . Bell demostró entonces que la física cuántica predice correlaciones que violan esta desigualdad . En los años siguientes se propusieron múltiples variaciones del teorema de Bell, utilizando diferentes supuestos y obteniendo diferentes desigualdades de Bell (o "tipo Bell").

El primer experimento rudimentario diseñado para probar el teorema de Bell fue realizado en 1972 por John Clauser y Stuart Freedman . ^[2] Experimentos más avanzados, conocidos colectivamente como pruebas de Bell , se han realizado muchas veces desde entonces. A menudo, estos experimentos han tenido el objetivo de "cerrar lagunas", es decir, mejorar problemas de diseño o configuración experimental que podrían en principio afectar la validez de los hallazgos de pruebas de Bell anteriores. Las pruebas de Bell han encontrado consistentemente que los sistemas físicos obedecen a la mecánica cuántica y violan las desigualdades de Bell; lo que quiere decir que los resultados de estos experimentos son incompatibles con las teorías de variables ocultas locales. ^{[3] [4]}

La naturaleza exacta de los supuestos necesarios para demostrar una restricción de tipo Bell sobre las correlaciones ha sido debatida por físicos y filósofos . Si bien la importancia del teorema de Bell no está en duda, las diferentes interpretaciones de la mecánica cuántica no se ponen de acuerdo sobre qué implica exactamente.

Existen muchas variaciones de la idea básica, algunas de las cuales emplean supuestos matemáticos más sólidos que otras. ^[5] Es significativo que los teoremas de tipo Bell no se refieran a ninguna teoría particular de variables ocultas locales, sino que muestran que la física cuántica viola los supuestos generales que sustentan las representaciones clásicas de la naturaleza. El teorema original demostrado por Bell en 1964 no es el más adecuado para la experimentación, y es conveniente introducir el género de las desigualdades de tipo Bell con un ejemplo posterior. ^[6]

Los personajes hipotéticos Alice y Bob se encuentran en lugares muy separados. Su colega Víctor prepara un par de partículas y envía una a Alice y la otra a Bob. Cuando Alice recibe su partícula, elige realizar una de dos mediciones posibles (quizás lanzando una moneda para decidir cuál). Denotemos estas mediciones con y . Tanto y son mediciones binarias : el resultado de es o , y lo mismo para . Cuando Bob recibe su partícula, elige una de dos mediciones, y , que también son binarias.${\estilo de visualización A_{0}}$$Estilo de visualización A_{1}$${\estilo de visualización A_{0}}$$Estilo de visualización A_{1}$${\estilo de visualización A_{0}}$${\estilo de visualización +1}$${\estilo de visualización -1}$$Estilo de visualización A_{1}$$Estilo de visualización B_{0}$$Estilo de visualización B_{1}$

Supongamos que cada medición revela una propiedad que la partícula ya poseía. Por ejemplo, si Alice elige medir y obtiene el resultado , entonces la partícula que recibió tenía un valor de para una propiedad . ^{[nota 1]} Considere la combinación Debido a que tanto y toman los valores , entonces o bien o . En el primer caso, la cantidad debe ser igual a 0, mientras que en el segundo caso, . Por lo tanto, uno de los términos del lado derecho de la expresión anterior desaparecerá y el otro será igual a . En consecuencia, si el experimento se repite en muchos ensayos, con Víctor preparando nuevos pares de partículas, el valor absoluto del promedio de la combinación en todos los ensayos será menor o igual a 2. Ningún ensayo individual puede medir esta cantidad, porque Alice y Bob solo pueden elegir una medición cada uno, pero en el supuesto de que existan las propiedades subyacentes, el valor promedio de la suma es simplemente la suma de los promedios para cada término. Uso de corchetes angulares para denotar promedios Esta es una desigualdad de Bell, específicamente, la desigualdad CHSH . ^{[6] : 115} Su derivación aquí depende de dos supuestos: primero, que las propiedades físicas subyacentes y existen independientemente de ser observadas o medidas (a veces llamado el supuesto de realismo ); y segundo, que la elección de acción de Alice no puede influir en el resultado de Bob o viceversa (a menudo llamado el supuesto de localidad ). ^{[6] : 117}${\estilo de visualización A_{0}}$${\estilo de visualización +1}$${\estilo de visualización +1}$${\displaystyle a_{0}}$$${\displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1})b_{0}+(a_{0}-a_{1})b_{1}\,.}$$${\displaystyle a_{0}}$$estilo de visualización a_{1}$${\estilo de visualización \pm 1}$$Estilo de visualización a_{0}=a_{1}$${\displaystyle a_{0}=-a_{1}}$${\displaystyle (a_{0}-a_{1})b_{1}}$${\displaystyle (a_{0}+a_{1})b_{0}=0}$${\displaystyle \pm 2}$${\displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}}$$${\displaystyle |\langle A_{0}B_{0}\rangle +\langle A_{0}B_{1}\rangle +\langle A_{1}B_{0}\rangle -\langle A_{1}B_{1}\rangle |\leq 2\,.}$$${\displaystyle a_{0},a_{1},b_{0},}$${\displaystyle b_{1}}$

La mecánica cuántica puede violar la desigualdad CHSH, de la siguiente manera. Víctor prepara un par de qubits que describe mediante el estado de Bell donde y son los estados propios de una de las matrices de Pauli , Víctor luego pasa el primer qubit a Alice y el segundo a Bob. Las elecciones de Alice y Bob de posibles mediciones también se definen en términos de las matrices de Pauli. Alice mide cualquiera de los dos observables y : y Bob mide cualquiera de los dos observables Víctor puede calcular los valores de expectativa cuántica para pares de estos observables utilizando la regla de Born : Si bien solo se puede realizar una de estas cuatro mediciones en un solo ensayo del experimento, la suma da la suma de los valores promedio que Víctor espera encontrar en múltiples ensayos. Este valor excede el límite superior clásico de 2 que se dedujo de la hipótesis de variables ocultas locales. ^{[6] : 116} El valor es, de hecho, el más grande que la física cuántica permite para esta combinación de valores de expectativa, lo que lo convierte en un límite de Tsirelson . ^{[9] : 140}$${\displaystyle |\psi \rangle ={\frac {|0\rangle \otimes |1\rangle -|1\rangle \otimes |0\rangle }{\sqrt {2}}},}$$${\displaystyle |0\rangle }$${\displaystyle |1\rangle }$$${\displaystyle \sigma _{z}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.}$$${\displaystyle \sigma _{z}}$${\displaystyle \sigma _{x}}$$${\displaystyle A_{0}=\sigma _{z},\ A_{1}=\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}};}$$$${\displaystyle B_{0}=-{\frac {\sigma _{x}+\sigma _{z}}{\sqrt {2}}},\ B_{1}={\frac {\sigma _{x}-\sigma _{z}}{\sqrt {2}}}.}$$$${\displaystyle \langle A_{0}\otimes B_{0}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{0}\otimes B_{1}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{1}\otimes B_{0}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{1}\otimes B_{1}\rangle =-{\frac {1}{\sqrt {2}}}\,.}$$$${\displaystyle \langle A_{0}\otimes B_{0}\rangle +\langle A_{0}\otimes B_{1}\rangle +\langle A_{1}\otimes B_{0}\rangle -\langle A_{1}\otimes B_{1}\rangle =2{\sqrt {2}}}$$${\displaystyle 2{\sqrt {2}}}$

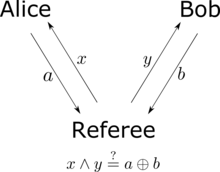
La desigualdad CHSH también puede considerarse como un juego en el que Alice y Bob intentan coordinar sus acciones . ^{[10] [11]} Víctor prepara dos bits, y , de forma independiente y aleatoria. Envía bit a Alice y bit a Bob. Alice y Bob ganan si devuelven bits de respuesta y a Víctor, satisfaciendo O, equivalentemente, Alice y Bob ganan si el AND lógico de y es el XOR lógico de y . Alice y Bob pueden acordar cualquier estrategia que deseen antes del juego, pero no pueden comunicarse una vez que el juego comienza. En cualquier teoría basada en variables ocultas locales, la probabilidad de Alice y Bob de ganar no es mayor que , independientemente de la estrategia que acuerden de antemano. Sin embargo, si comparten un estado cuántico entrelazado, su probabilidad de ganar puede ser tan grande como${\displaystyle x}$${\displaystyle y}$${\displaystyle x}$${\displaystyle y}$${\displaystyle a}$${\displaystyle b}$$${\displaystyle xy=a+b\mod 2\,.}$$${\displaystyle x}$${\displaystyle y}$${\displaystyle a}$${\displaystyle b}$${\displaystyle 3/4}$$${\displaystyle {\frac {2+{\sqrt {2}}}{4}}\approx 0.85\,.}$$

El artículo de Bell de 1964 señala que, en condiciones restringidas, los modelos locales de variables ocultas pueden reproducir las predicciones de la mecánica cuántica. Luego demuestra que esto no puede ser cierto en general. ^[12] Bell considera un refinamiento de David Bohm del experimento mental de Einstein-Podolsky-Rosen (EPR). En este escenario, un par de partículas se forman juntas de tal manera que se describen por un estado singlete de espín (que es un ejemplo de un estado entrelazado). Las partículas luego se separan en direcciones opuestas. Cada partícula se mide con un dispositivo Stern-Gerlach , un instrumento de medición que se puede orientar en diferentes direcciones y que informa uno de dos resultados posibles, representables por y . La configuración de cada instrumento de medición está representada por un vector unitario , y la predicción mecánico-cuántica para la correlación entre dos detectores con configuraciones y es En particular, si la orientación de los dos detectores es la misma ( ), entonces el resultado de una medición es seguro que será el negativo del resultado de la otra, dando . Y si las orientaciones de los dos detectores son ortogonales ( ), entonces los resultados no están correlacionados y . Bell demuestra con un ejemplo que estos casos especiales pueden explicarse en términos de variables ocultas, y luego procede a demostrar que el rango completo de posibilidades que involucran ángulos intermedios no puede .${\displaystyle +1}$${\displaystyle -1}$${\displaystyle {\vec {a}}}$${\displaystyle {\vec {b}}}$$${\displaystyle P({\vec {a}},{\vec {b}})=-{\vec {a}}\cdot {\vec {b}}.}$$${\displaystyle {\vec {a}}={\vec {b}}}$${\displaystyle P({\vec {a}},{\vec {a}})=-1}$${\displaystyle {\vec {a}}\cdot {\vec {b}}=0}$${\displaystyle P({\vec {a}},{\vec {b}})=0}$

Bell postuló que un modelo local de variable oculta para estas correlaciones las explicaría en términos de una integral sobre los posibles valores de algún parámetro oculto : donde es una función de densidad de probabilidad . Las dos funciones y proporcionan las respuestas de los dos detectores dados los vectores de orientación y la variable oculta: De manera crucial, el resultado del detector no depende de , y del mismo modo, el resultado de no depende de , porque los dos detectores están separados físicamente. Ahora suponemos que el experimentador tiene una opción de configuración para el segundo detector: puede configurarse en o en . Bell demuestra que la diferencia en correlación entre estas dos opciones de configuración del detector debe satisfacer la desigualdad Sin embargo, es fácil encontrar situaciones en las que la mecánica cuántica viola la desigualdad de Bell. ^{[13] : 425–426} Por ejemplo, sean los vectores y ortogonales, y sean yacían en su plano en un ángulo de 45° con respecto a ambos. Entonces , mientras pero Por lo tanto, no existe un modelo local de variable oculta que pueda reproducir las predicciones de la mecánica cuántica para todas las opciones de , , y Los resultados experimentales contradicen las curvas clásicas y coinciden con la curva predicha por la mecánica cuántica siempre que se tengan en cuenta las deficiencias experimentales. ^[5]${\displaystyle \lambda }$$${\displaystyle P({\vec {a}},{\vec {b}})=\int d\lambda \,\rho (\lambda )A({\vec {a}},\lambda )B({\vec {b}},\lambda ),}$$${\displaystyle \rho (\lambda )}$${\displaystyle A({\vec {a}},\lambda )}$${\displaystyle B({\vec {b}},\lambda )}$$${\displaystyle A({\vec {a}},\lambda )=\pm 1,\,B({\vec {b}},\lambda )=\pm 1.}$$${\displaystyle A}$${\displaystyle {\vec {b}}}$${\displaystyle B}$${\displaystyle {\vec {a}}}$${\displaystyle {\vec {b}}}$${\displaystyle {\vec {c}}}$$${\displaystyle |P({\vec {a}},{\vec {b}})-P({\vec {a}},{\vec {c}})|\leq 1+P({\vec {b}},{\vec {c}}).}$$${\displaystyle {\vec {a}}}$${\displaystyle {\vec {b}}}$${\displaystyle {\vec {c}}}$$${\displaystyle P({\vec {a}},{\vec {b}})=0,}$$$${\displaystyle P({\vec {a}},{\vec {c}})=P({\vec {b}},{\vec {c}})=-{\frac {\sqrt {2}}{2}},}$$$${\displaystyle {\frac {\sqrt {2}}{2}}\nleq 1-{\frac {\sqrt {2}}{2}}.}$$${\displaystyle {\vec {a}}}$${\displaystyle {\vec {b}}}$${\displaystyle {\vec {c}}.}$

El teorema de Bell de 1964 requiere la posibilidad de anticorrelaciones perfectas: la capacidad de hacer una predicción de probabilidad 1 sobre el resultado del segundo detector, conociendo el resultado del primero. Esto está relacionado con el "criterio de realidad EPR", un concepto introducido en el artículo de 1935 de Einstein, Podolsky y Rosen. Este artículo postula: "Si, sin alterar de ninguna manera un sistema, podemos predecir con certeza (es decir, con probabilidad igual a la unidad) el valor de una cantidad física, entonces existe un elemento de realidad correspondiente a esa cantidad". ^[14]

Daniel Greenberger , Michael A. Horne y Anton Zeilinger presentaron un experimento mental de cuatro partículas en 1990, que David Mermin luego simplificó para usar solo tres partículas. ^{[15] [16]} En este experimento mental, Victor genera un conjunto de tres partículas de espín 1/2 descritas por el estado cuántico donde como se indicó anteriormente, y son los vectores propios de la matriz de Pauli . Luego, Victor envía una partícula a Alice, Bob y Charlie, quienes esperan en ubicaciones muy separadas. Alice mide o en su partícula, y también lo hacen Bob y Charlie. El resultado de cada medición es o . Aplicando la regla de Born al estado de tres qubits , Victor predice que siempre que las tres mediciones incluyan uno y dos , el producto de los resultados siempre será . Esto se deduce porque es un vector propio de con valor propio , y lo mismo para y . Por lo tanto, conociendo el resultado de Alice para una medición y el resultado de Bob para una medición, Victor puede predecir con probabilidad 1 qué resultado devolverá Charlie para una medición . Según el criterio de realidad EPR, habría un "elemento de realidad" correspondiente al resultado de una medición sobre el cúbit de Charlie. De hecho, esta misma lógica se aplica a ambas mediciones y a los tres cúbits. De acuerdo con el criterio de realidad EPR, entonces, cada partícula contiene un "conjunto de instrucciones" que determina el resultado de una medición o sobre ella. El conjunto de las tres partículas se describiría entonces mediante el conjunto de instrucciones, donde cada entrada sería o y cada medición o simplemente devolvería el valor apropiado.$${\displaystyle |\psi \rangle ={\frac {1}{\sqrt {2}}}(|000\rangle -|111\rangle )\,,}$$${\displaystyle |0\rangle }$${\displaystyle |1\rangle }$${\displaystyle \sigma _{z}}$${\displaystyle \sigma _{x}}$${\displaystyle \sigma _{y}}$${\displaystyle +1}$${\displaystyle -1}$${\displaystyle |\psi \rangle }$${\displaystyle \sigma _{x}}$${\displaystyle \sigma _{y}}$${\displaystyle +1}$${\displaystyle |\psi \rangle }$${\displaystyle \sigma _{x}\otimes \sigma _{y}\otimes \sigma _{y}}$${\displaystyle +1}$${\displaystyle \sigma _{y}\otimes \sigma _{x}\otimes \sigma _{y}}$${\displaystyle \sigma _{y}\otimes \sigma _{y}\otimes \sigma _{x}}$${\displaystyle \sigma _{x}}$${\displaystyle \sigma _{y}}$${\displaystyle \sigma _{y}}$${\displaystyle \sigma _{y}}$${\displaystyle \sigma _{x}}$${\displaystyle \sigma _{y}}$$${\displaystyle (a_{x},a_{y},b_{x},b_{y},c_{x},c_{y})\,,}$$${\displaystyle -1}$${\displaystyle +1}$${\displaystyle \sigma _{x}}$${\displaystyle \sigma _{y}}$

Si Alice, Bob y Charlie realizan la medición, entonces el producto de sus resultados sería . Este valor se puede deducir de porque el cuadrado de o es . Cada factor entre paréntesis es igual a , por lo que y el producto de los resultados de Alice, Bob y Charlie será con probabilidad unitaria. Pero esto es incompatible con la física cuántica: Víctor puede predecir usando el estado que la medición producirá en cambio con probabilidad unitaria.${\displaystyle \sigma _{x}}$${\displaystyle a_{x}b_{x}c_{x}}$$${\displaystyle (a_{x}b_{y}c_{y})(a_{y}b_{x}c_{y})(a_{y}b_{y}c_{x})=a_{x}b_{x}c_{x}a_{y}^{2}b_{y}^{2}c_{y}^{2}=a_{x}b_{x}c_{x}\,,}$$${\displaystyle -1}$${\displaystyle +1}$${\displaystyle 1}$${\displaystyle +1}$$${\displaystyle a_{x}b_{x}c_{x}=+1\,,}$$${\displaystyle +1}$${\displaystyle |\psi \rangle }$${\displaystyle \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}}$${\displaystyle -1}$

Este experimento mental también puede reformularse como una desigualdad de Bell tradicional o, equivalentemente, como un juego no local en el mismo espíritu que el juego CHSH. ^[17] En él, Alice, Bob y Charlie reciben bits de Victor, a quienes se les promete que siempre tendrán un número par de unos, es decir, , y le envían de vuelta bits . Ganan el juego si tienen un número impar de unos para todas las entradas excepto , cuando necesitan tener un número par de unos. Es decir, ganan el juego si y solo si . Con variables ocultas locales, la probabilidad más alta de victoria que pueden tener es 3/4, mientras que usando la estrategia cuántica anterior lo ganan con certeza. Este es un ejemplo de pseudotelepatía cuántica .${\displaystyle x,y,z}$${\displaystyle x\oplus y\oplus z=0}$${\displaystyle a,b,c}$${\displaystyle a,b,c}$${\displaystyle x=y=z=0}$${\displaystyle a\oplus b\oplus c=x\lor y\lor z}$

En teoría cuántica, las bases ortonormales para un espacio de Hilbert representan mediciones que pueden realizarse sobre un sistema que tenga ese espacio de Hilbert. Cada vector en una base representa un posible resultado de esa medición. ^{[nota 2]} Supongamos que existe una variable oculta , de modo que conocer el valor de implicaría certeza sobre el resultado de cualquier medición. Dado un valor de , cada resultado de medición, es decir, cada vector en el espacio de Hilbert, es imposible o está garantizado. Una configuración de Kochen-Specker es un conjunto finito de vectores formado por múltiples bases entrelazadas, con la propiedad de que un vector en él siempre será imposible cuando se considere que pertenece a una base y estará garantizado cuando se tome como perteneciente a otra. En otras palabras, una configuración de Kochen-Specker es un "conjunto incoloro" que demuestra la inconsistencia de suponer que una variable oculta puede controlar los resultados de la medición. ^{[22] : 196–201}${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle \lambda }$

El tipo de argumento de Kochen-Specker, que utiliza configuraciones de bases entrelazadas, se puede combinar con la idea de medir pares entrelazados que subyace a las desigualdades de tipo Bell. Esto fue observado a principios de la década de 1970 por Kochen, ^[23] Heywood y Redhead, ^[24] Stairs, ^[25] y Brown y Svetlichny. ^[26] Como señaló EPR, obtener un resultado de medición en una mitad de un par entrelazado implica certeza sobre el resultado de una medición correspondiente en la otra mitad. El "criterio de realidad de EPR" postula que debido a que la segunda mitad del par no fue alterada, esa certeza debe deberse a una propiedad física que le pertenece. ^[27] En otras palabras, según este criterio, debe existir una variable oculta dentro de la segunda mitad del par, aún no medida. No surge ninguna contradicción si solo se considera una medición en la primera mitad. Sin embargo, si el observador puede elegir entre múltiples mediciones posibles, y los vectores que definen esas mediciones forman una configuración de Kochen-Specker, entonces algún resultado en la segunda mitad será simultáneamente imposible y garantizado.${\displaystyle \lambda }$

Este tipo de argumento ganó atención cuando John Conway y Simon Kochen propusieron un ejemplo del mismo bajo el nombre de teorema del libre albedrío . ^{[28] [29] [30]} El teorema de Conway-Kochen utiliza un par de qutrits entrelazados y una configuración de Kochen-Specker descubierta por Asher Peres . ^[31]

Como señaló Bell, algunas predicciones de la mecánica cuántica se pueden replicar en modelos locales de variables ocultas, incluidos casos especiales de correlaciones producidas a partir del entrelazamiento. Este tema se ha estudiado sistemáticamente en los años transcurridos desde el teorema de Bell. En 1989, Reinhard Werner introdujo lo que ahora se denominan estados de Werner , estados cuánticos conjuntos para un par de sistemas que producen correlaciones de tipo EPR pero que también admiten un modelo de variable oculta. ^[32] Los estados de Werner son estados cuánticos bipartitos que son invariantes bajo unitarios de forma simétrica de producto tensorial : En 2004, Robert Spekkens introdujo un modelo de juguete que comienza con la premisa de grados de libertad locales discretizados y luego impone un "principio de equilibrio de conocimiento" que restringe cuánto puede saber un observador sobre esos grados de libertad, convirtiéndolos así en variables ocultas. Los estados de conocimiento permitidos ("estados epistémicos") sobre las variables subyacentes ("estados ónticos") imitan algunas características de los estados cuánticos. Las correlaciones en el modelo de juguete pueden emular algunos aspectos del entrelazamiento, como la monogamia , pero por construcción, el modelo de juguete nunca puede violar una desigualdad de Bell. ^{[33] [34]}$${\displaystyle \rho _{AB}=(U\otimes U)\rho _{AB}(U^{\dagger }\otimes U^{\dagger }).}$$

La cuestión de si la mecánica cuántica puede ser "completada" por variables ocultas data de los primeros años de la teoría cuántica. En su libro de texto de 1932 sobre mecánica cuántica , el polímata nacido en Hungría John von Neumann presentó lo que él afirmaba ser una prueba de que no podía haber "parámetros ocultos". La validez y la concreción de la prueba de von Neumann fueron cuestionadas por Hans Reichenbach , con más detalle por Grete Hermann y posiblemente en una conversación, aunque no en forma impresa, por Albert Einstein. ^{[nota 3]} ( Simon Kochen y Ernst Specker rechazaron la suposición clave de von Neumann ya en 1961, pero no publicaron una crítica de ella hasta 1967. ^[40] )

Einstein sostuvo con insistencia que la mecánica cuántica no podía ser una teoría completa. Su argumento preferido se basaba en un principio de localidad:

Consideremos un sistema mecánico constituido por dos sistemas parciales A y B que interactúan entre sí sólo durante un tiempo limitado. Sea dada la función ψ antes de su interacción. Entonces, la ecuación de Schrödinger proporcionará la función ψ después de que haya tenido lugar su interacción. Determinemos ahora la condición física del sistema parcial A de la forma más completa posible mediante mediciones. Entonces, la mecánica cuántica nos permite determinar la función ψ del sistema parcial B a partir de las mediciones realizadas y de la función ψ del sistema total. Esta determinación, sin embargo, da un resultado que depende de cuál de las magnitudes determinantes que especifican la condición de A se haya medido (por ejemplo, coordenadas o momentos). Dado que sólo puede haber una condición física de B después de la interacción y que razonablemente no puede considerarse dependiente de la medición particular que realizamos en el sistema A separado de B, se puede concluir que la función ψ no está coordinada inequívocamente con la condición física. Esta coordinación de varias funciones ψ con la misma condición física del sistema B muestra nuevamente que la función ψ no puede interpretarse como una descripción (completa) de una condición física de un sistema unitario. ^[41]

El experimento mental EPR es similar, considerando también dos sistemas separados A y B descritos por una función de onda conjunta. Sin embargo, el artículo EPR añade la idea conocida posteriormente como el criterio EPR de realidad, según el cual la capacidad de predecir con probabilidad 1 el resultado de una medición en B implica la existencia de un "elemento de realidad" dentro de B. [ ^42]

En 1951, David Bohm propuso una variante del experimento mental EPR en el que las mediciones tienen rangos discretos de resultados posibles, a diferencia de las mediciones de posición y momento consideradas por EPR. ^[43] El año anterior, Chien-Shiung Wu e Irving Shaknov habían medido con éxito las polarizaciones de fotones producidos en pares entrelazados, haciendo así que la versión de Bohm del experimento mental EPR fuera prácticamente factible. ^[44]

A finales de la década de 1940, el matemático George Mackey se había interesado por los fundamentos de la física cuántica y en 1957 elaboró ​​una lista de postulados que tomó como una definición precisa de la mecánica cuántica. ^[45] Mackey conjeturó que uno de los postulados era redundante y, poco después, Andrew M. Gleason demostró que, de hecho, era deducible de los otros postulados. ^{[46] [47]} El teorema de Gleason proporcionó un argumento de que una amplia clase de teorías de variables ocultas son incompatibles con la mecánica cuántica. ^{[nota 4]} Más específicamente, el teorema de Gleason descarta los modelos de variables ocultas que son "no contextuales". Cualquier modelo de variable oculta para la mecánica cuántica debe, para evitar las implicaciones del teorema de Gleason, involucrar variables ocultas que no sean propiedades que pertenecen solo al sistema medido sino que también dependen del contexto externo en el que se realiza la medición. Este tipo de dependencia a menudo se considera artificial o indeseable; En algunos contextos, es incompatible con la relatividad especial . ^{[49] [50]} El teorema de Kochen-Specker refina esta afirmación al construir un subconjunto finito específico de rayos en los que no se puede definir tal medida de probabilidad. ^{[49] [51]}

Tsung-Dao Lee estuvo cerca de derivar el teorema de Bell en 1960. Consideró eventos en los que se producían dos kaones que viajaban en direcciones opuestas y llegó a la conclusión de que las variables ocultas no podían explicar las correlaciones que se podían obtener en tales situaciones. Sin embargo, surgieron complicaciones debido al hecho de que los kaones se desintegran, y no llegó a deducir una desigualdad de tipo Bell. ^{[36] : 308}

Bell eligió publicar su teorema en una revista relativamente poco conocida porque no requería el cobro por página , de hecho pagaba a los autores que publicaban allí en ese momento. Sin embargo, como la revista no proporcionaba reimpresiones gratuitas de artículos para que los autores los distribuyeran, Bell tuvo que gastar el dinero que recibió para comprar copias que pudiera enviar a otros físicos. ^[52] Si bien los artículos impresos en la revista en sí mismos enumeraban el nombre de la publicación simplemente como Physics , las cubiertas llevaban la versión trilingüe Physics Physique Физика para reflejar que imprimiría artículos en inglés, francés y ruso. ^{[39] : 92–100, 289}

Antes de demostrar su resultado de 1964, Bell también demostró un resultado equivalente al teorema de Kochen-Specker (de ahí que este último también se conozca a veces como teorema de Bell-Kochen-Specker o teorema de Bell-KS). Sin embargo, la publicación de este teorema se retrasó inadvertidamente hasta 1966. ^{[49] [53]} En ese artículo, Bell argumentó que debido a que una explicación de los fenómenos cuánticos en términos de variables ocultas requeriría no localidad, la paradoja EPR "se resuelve de la manera que a Einstein menos le hubiera gustado". ^[53]

En 1967, el inusual título Physics Physique Физика llamó la atención de John Clauser , quien luego descubrió el artículo de Bell y comenzó a considerar cómo realizar una prueba de Bell en el laboratorio. ^[54] Clauser y Stuart Freedman continuaron realizando una prueba de Bell en 1972. ^{[55] [56]} Esta fue solo una prueba limitada, porque la elección de los ajustes del detector se realizó antes de que los fotones abandonaran la fuente. En 1982, Alain Aspect y colaboradores realizaron la primera prueba de Bell para eliminar esta limitación. ^[57] Esto inició una tendencia de pruebas de Bell progresivamente más estrictas. El experimento mental GHZ se implementó en la práctica, utilizando tripletes entrelazados de fotones, en 2000. ^[58] Para 2002, probar la desigualdad CHSH era factible en cursos de laboratorio de pregrado. ^[59]

En las pruebas de Bell, pueden existir problemas de diseño o configuración experimental que afecten la validez de los hallazgos experimentales. Estos problemas se conocen a menudo como "lagunas". El propósito del experimento es comprobar si la naturaleza puede describirse mediante la teoría de variables ocultas locales , lo que contradiría las predicciones de la mecánica cuántica.

Las lagunas más frecuentes en los experimentos reales son las lagunas de detección y de localidad . ^[60] La laguna de detección se abre cuando se detecta una pequeña fracción de las partículas (normalmente fotones) en el experimento, lo que permite explicar los datos con variables ocultas locales suponiendo que las partículas detectadas son una muestra no representativa. La laguna de localidad se abre cuando las detecciones no se realizan con una separación espacial , lo que hace posible que el resultado de una medición influya en la otra sin contradecir la relatividad. En algunos experimentos puede haber defectos adicionales que hagan posibles las explicaciones de las violaciones de la prueba de Bell mediante variables ocultas locales. ^[61]

Aunque tanto las lagunas de localización como las de detección se habían cerrado en diferentes experimentos, un desafío de larga data era cerrar ambas simultáneamente en el mismo experimento. Esto finalmente se logró en tres experimentos en 2015. ^{[62] [63] [64] [65] [66]} Con respecto a estos resultados, Alain Aspect escribe que "no se puede decir que ningún experimento ... esté totalmente libre de lagunas", pero dice que los experimentos "eliminan las últimas dudas de que deberíamos renunciar" a las variables ocultas locales, y se refiere a ejemplos de lagunas restantes como "inverosímiles" y "ajenos a la forma habitual de razonamiento en física". ^[67]

Estos esfuerzos por validar experimentalmente las violaciones de las desigualdades de Bell darían más tarde como resultado que Clauser, Aspect y Anton Zeilinger recibieran el Premio Nobel de Física de 2022. ^[68]

Las reacciones al teorema de Bell han sido muchas y variadas. Maximilian Schlosshauer, Johannes Kofler y Zeilinger escriben que las desigualdades de Bell proporcionan "un ejemplo maravilloso de cómo podemos tener un resultado teórico riguroso probado mediante numerosos experimentos y, sin embargo, estar en desacuerdo sobre las implicaciones". ^[69]

Las interpretaciones de tipo Copenhague generalmente toman la violación de las desigualdades de Bell como base para rechazar el supuesto a menudo llamado definitividad contrafáctica o "realismo", que no es necesariamente lo mismo que abandonar el realismo en un sentido filosófico más amplio. ^{[70] [71]} Por ejemplo, Roland Omnès argumenta a favor del rechazo de las variables ocultas y concluye que "la mecánica cuántica es probablemente tan realista como cualquier teoría de su alcance y madurez lo será jamás". ^{[72] : 531} Del mismo modo, Rudolf Peierls tomó el mensaje del teorema de Bell como que, debido a que la premisa de localidad es físicamente razonable, "las variables ocultas no pueden introducirse sin abandonar algunos de los resultados de la mecánica cuántica". ^{[73] [74]}

Éste es también el camino que siguen las interpretaciones que descienden de la tradición de Copenhague, como las historias consistentes (a menudo publicitadas como "Copenhague bien hecha"), ^{[75] :  2839} así como el QBismo . ^[76]

La interpretación de los muchos mundos , también conocida como interpretación de Everett , es dinámicamente local, lo que significa que no requiere una acción a distancia , ^{[77] : 17} y determinista, porque consiste en la parte unitaria de la mecánica cuántica sin colapso. Puede generar correlaciones que violan una desigualdad de Bell porque viola una suposición implícita de Bell de que las mediciones tienen un único resultado. De hecho, el teorema de Bell se puede demostrar en el marco de los muchos mundos a partir de la suposición de que una medición tiene un único resultado. Por lo tanto, una violación de una desigualdad de Bell se puede interpretar como una demostración de que las mediciones tienen múltiples resultados. ^[78]

La explicación que proporciona para las correlaciones de Bell es que cuando Alice y Bob hacen sus mediciones, se dividen en ramas locales. Desde el punto de vista de cada copia de Alice, hay múltiples copias de Bob que experimentan resultados diferentes, por lo que Bob no puede tener un resultado definido, y lo mismo es cierto desde el punto de vista de cada copia de Bob. Obtendrán un resultado mutuamente bien definido solo cuando sus futuros conos de luz se superpongan. En este punto podemos decir que la correlación de Bell comienza a existir, pero fue producida por un mecanismo puramente local. Por lo tanto, la violación de una desigualdad de Bell no puede interpretarse como una prueba de no localidad. ^{[77] :  28}

La mayoría de los defensores de la idea de las variables ocultas creen que los experimentos han descartado las variables ocultas locales. ^{[nota 5]} Están dispuestos a renunciar a la localidad, explicando la violación de la desigualdad de Bell por medio de una teoría de variables ocultas no locales , en la que las partículas intercambian información sobre sus estados. Esta es la base de la interpretación de Bohm de la mecánica cuántica, que requiere que todas las partículas en el universo puedan intercambiar información instantáneamente con todas las demás. Un desafío para las teorías de variables ocultas no locales es explicar por qué esta comunicación instantánea puede existir a nivel de las variables ocultas, pero no puede usarse para enviar señales. ^[81] Un experimento de 2007 descartó una gran clase de teorías de variables ocultas no locales no bohmianas, aunque no la mecánica bohmiana en sí. ^[82]

La interpretación transaccional , que postula que las ondas viajan tanto hacia atrás como hacia adelante en el tiempo, también es no local. ^[83]

Un supuesto necesario para derivar el teorema de Bell es que las variables ocultas no están correlacionadas con los parámetros de medición. Este supuesto se ha justificado con el argumento de que el experimentador tiene " libre albedrío " para elegir los parámetros y que es necesario para hacer ciencia en primer lugar. Una teoría (hipotética) en la que la elección de la medición está necesariamente correlacionada con el sistema que se mide se conoce como superdeterminista . ^[60]

Algunos defensores de los modelos deterministas no han abandonado la idea de que las variables ocultas locales son válidas. Por ejemplo, Gerard 't Hooft ha sostenido que no se puede descartar el superdeterminismo. ^[84]

Lo siguiente está destinado al público general.

• Aczel, Amir D. (2001). Entrelazamiento: el mayor misterio de la física . Nueva York: Four Walls Eight Windows.
• Afriat, A.; Selleri, F. (1999). La paradoja de Einstein, Podolsky y Rosen . Nueva York y Londres: Plenum Press.
• Baggott, J. (1992). El significado de la teoría cuántica . Oxford University Press.
• Gilder, Louisa (2008). La era del entrelazamiento: cuando renació la física cuántica . Nueva York: Alfred A. Knopf.
• Greene, Brian (2004). El tejido del cosmos . Vintage. ISBN 0-375-72720-5.
• Mermin, N. David (1981). "Trayendo a casa el mundo atómico: misterios cuánticos para cualquiera". American Journal of Physics . 49 (10): 940–943. Bibcode :1981AmJPh..49..940M. doi :10.1119/1.12594. S2CID  122724592.
• Mermin, N. David (abril de 1985). "¿Está la luna allí cuando nadie la mira? La realidad y la teoría cuántica". Physics Today . 38 (4): 38–47. Bibcode :1985PhT....38d..38M. doi :10.1063/1.880968.

Los siguientes tienen una orientación más técnica.

Wikilibros tiene un libro sobre el tema: Mecánica cuántica

Wikiversidad tiene recursos de aprendizaje sobre el teorema de Bell

Wikimedia Commons alberga una categoría multimedia sobre Teorema de Bell .

• Mermin: ¿Acciones espeluznantes a distancia? Conferencia de Oppenheimer.
• "Teorema de Bell". Enciclopedia de Filosofía en Internet .
• "Desigualdades de Bell". Enciclopedia de Matemáticas . EMS Press . 2001 [1994].