Experimento de Stern-Gerlach

| Parte de una serie de artículos sobre |
| Mecánica cuántica |
|---|
En física cuántica , el experimento de Stern-Gerlach demostró que la orientación espacial del momento angular está cuantizada . De este modo, se demostró que un sistema a escala atómica tiene propiedades intrínsecamente cuánticas. En el experimento original, se enviaron átomos de plata a través de un campo magnético variable espacialmente , que los desvió antes de que chocaran con una pantalla detectora, como un portaobjetos de vidrio. Las partículas con un momento magnético distinto de cero se desviaron, debido al gradiente del campo magnético , de una trayectoria recta. La pantalla reveló puntos discretos de acumulación, en lugar de una distribución continua, [1] debido a su espín cuantizado . Históricamente, este experimento fue decisivo para convencer a los físicos de la realidad de la cuantización del momento angular en todos los sistemas a escala atómica. [2] [3] [4]
Después de su concepción por Otto Stern en 1921, el experimento se llevó a cabo con éxito por primera vez con Walther Gerlach a principios de 1922. [1] [5] [6]
Descripción
El experimento de Stern-Gerlach consiste en enviar átomos de plata a través de un campo magnético no homogéneo y observar su desviación. Los átomos de plata se evaporaron utilizando un horno eléctrico en el vacío. Utilizando rendijas delgadas, los átomos fueron guiados hacia un haz plano y el haz se envió a través de un campo magnético no homogéneo antes de colisionar con una placa metálica. Las leyes de la física clásica predicen que la colección de átomos de plata condensados en la placa debe formar una línea sólida delgada con la misma forma que el haz original. Sin embargo, el campo magnético no homogéneo hizo que el haz se dividiera en dos direcciones separadas, creando dos líneas en la placa metálica.
Los resultados muestran que las partículas poseen un momento angular intrínseco que es muy análogo al momento angular de un objeto que gira de forma clásica, pero que solo toma ciertos valores cuantizados. Otro resultado importante es que solo se puede medir un componente del giro de una partícula a la vez, lo que significa que la medición del giro a lo largo del eje z destruye la información sobre el giro de una partícula a lo largo de los ejes x e y.
El experimento se lleva a cabo normalmente utilizando partículas eléctricamente neutras , como átomos de plata. Esto evita la gran desviación en la trayectoria de una partícula cargada que se mueve a través de un campo magnético y permite que predominen los efectos dependientes del espín. [7] [8]
Si la partícula se trata como un dipolo magnético giratorio clásico , precesará en un campo magnético debido al par que el campo magnético ejerce sobre el dipolo (ver precesión inducida por par ). Si se mueve a través de un campo magnético homogéneo, las fuerzas ejercidas en los extremos opuestos del dipolo se cancelan entre sí y la trayectoria de la partícula no se ve afectada. Sin embargo, si el campo magnético no es homogéneo, la fuerza en un extremo del dipolo será ligeramente mayor que la fuerza opuesta en el otro extremo, de modo que hay una fuerza neta que desvía la trayectoria de la partícula. Si las partículas fueran objetos giratorios clásicos, uno esperaría que la distribución de sus vectores de momento angular de espín fuera aleatoria y continua . Cada partícula se desviaría en una cantidad proporcional al producto escalar de su momento magnético con el gradiente de campo externo, produciendo una cierta distribución de densidad en la pantalla del detector. En cambio, las partículas que pasan a través del aparato de Stern-Gerlach se desvían hacia arriba o hacia abajo en una cantidad específica. Esta fue una medición del observable cuántico ahora conocido como momento angular de espín , que demostró los posibles resultados de una medición donde el observable tiene un conjunto discreto de valores o espectro de puntos . [9]
Aunque algunos fenómenos cuánticos discretos, como los espectros atómicos , se observaron mucho antes, el experimento de Stern-Gerlach permitió a los científicos observar directamente la separación entre estados cuánticos discretos por primera vez.
En teoría, el momento angular cuántico de cualquier tipo tiene un espectro discreto , que a veces se expresa brevemente como "el momento angular está cuantizado ".
Experimento utilizando partículas con espín +1/2 o −1/2
Si el experimento se lleva a cabo utilizando partículas cargadas, como electrones, se generará una fuerza de Lorentz que tenderá a desviar la trayectoria en un círculo. Esta fuerza se puede anular mediante un campo eléctrico de magnitud adecuada orientado transversalmente a la trayectoria de la partícula cargada.

Los electrones son partículas de espín 1/2 . Estos tienen solo dos valores posibles de momento angular de espín medidos a lo largo de cualquier eje, o , un fenómeno puramente mecánico cuántico. Debido a que su valor es siempre el mismo, se considera una propiedad intrínseca de los electrones, y a veces se lo conoce como "momento angular intrínseco" (para distinguirlo del momento angular orbital, que puede variar y depende de la presencia de otras partículas). Si se mide el espín a lo largo de un eje vertical, los electrones se describen como "espín hacia arriba" o "espín hacia abajo", según el momento magnético que apunte hacia arriba o hacia abajo, respectivamente.
Para describir matemáticamente el experimento con partículas de espín, lo más fácil es utilizar la notación de bra-ket de Dirac . A medida que las partículas pasan a través del dispositivo de Stern-Gerlach, se desvían hacia arriba o hacia abajo y son observadas por el detector, que resuelve si tienen espín hacia arriba o hacia abajo. Estos se describen mediante el número cuántico de momento angular , que puede adoptar uno de los dos posibles valores permitidos, o bien o bien . El acto de observar (medir) el momento a lo largo del eje corresponde al operador de momento angular del eje , a menudo denotado como . En términos matemáticos, el estado inicial de las partículas es
donde las constantes y son números complejos. Este giro de estado inicial puede apuntar en cualquier dirección. Los cuadrados de los valores absolutos y son respectivamente las probabilidades de que un sistema en el estado se encuentre en y después de que se realice la medición a lo largo del eje. Las constantes y también deben normalizarse para que la probabilidad de encontrar cualquiera de los valores sea la unidad, es decir, debemos asegurarnos de que . Sin embargo, esta información no es suficiente para determinar los valores de y , porque son números complejos. Por lo tanto, la medición produce solo las magnitudes al cuadrado de las constantes, que se interpretan como probabilidades.
Experimentos secuenciales
Si vinculamos varios aparatos Stern-Gerlach (los rectángulos que contienen SG ), podemos ver claramente que no actúan como simples selectores, es decir, filtrando partículas con uno de los estados (preexistentes a la medición) y bloqueando los demás. En cambio, alteran el estado observándolo (como en la polarización de la luz ). En la figura siguiente, x y z nombran las direcciones del campo magnético (no homogéneo), siendo el plano xz ortogonal al haz de partículas. En los tres sistemas Stern-Gerlach que se muestran a continuación, los cuadrados rayados denotan el bloqueo de una salida dada, es decir, cada uno de los sistemas Stern-Gerlach con un bloqueador permite que solo las partículas con uno de los dos estados ingresen al siguiente aparato Stern-Gerlach en la secuencia. [10]
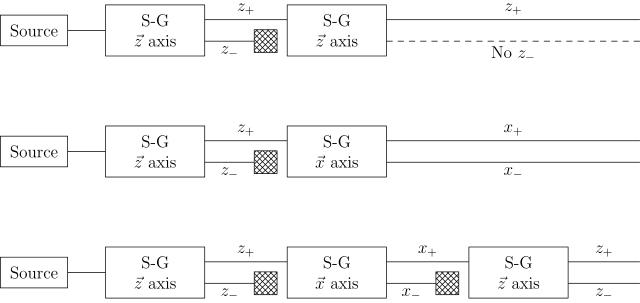

Experimento 1
La ilustración superior muestra que cuando se coloca un segundo aparato SG idéntico a la salida del primer aparato, solo se ve z+ en la salida del segundo aparato. Este resultado es previsible, ya que se espera que todas las partículas en este punto tengan espín z+, ya que solo el haz z+ del primer aparato entró en el segundo aparato. [11]

Experimento 2
El sistema intermedio muestra lo que sucede cuando se coloca un aparato SG diferente a la salida del haz z+ resultante del primer aparato, midiendo el segundo aparato la desviación de los haces en el eje x en lugar del eje z. El segundo aparato produce salidas x+ y x-. Ahora bien, clásicamente esperaríamos tener un haz con la característica x orientada a + y la característica z orientada a +, y otro con la característica x orientada a - y la característica z orientada a +. [11]

Experimento 3
El sistema inferior contradice esa expectativa. La salida del tercer aparato que mide la desviación en el eje z muestra nuevamente una salida de z- así como de z+. Dado que la entrada al segundo aparato SG consistía solo en z+ , se puede inferir que un aparato SG debe estar alterando los estados de las partículas que pasan a través de él. Este experimento puede interpretarse como una demostración del principio de incertidumbre : dado que el momento angular no se puede medir en dos direcciones perpendiculares al mismo tiempo, la medición del momento angular en la dirección x destruye la determinación previa del momento angular en la dirección z. Es por eso que el tercer aparato mide los rayos z+ y z- renovados como si la medición x realmente hiciera borrón y cuenta nueva de la salida z+. [11]
Historia

El experimento de Stern-Gerlach fue concebido por Otto Stern en 1921 y realizado por él y Walther Gerlach en Frankfurt en 1922. [10] En el momento del experimento, el modelo más frecuente para describir el átomo era el modelo de Bohr-Sommerfeld , [12] [13] que describía a los electrones como girando alrededor del núcleo cargado positivamente solo en ciertos orbitales atómicos discretos o niveles de energía . Dado que el electrón estaba cuantizado para estar solo en ciertas posiciones en el espacio, la separación en órbitas distintas se denominó cuantización espacial . El experimento de Stern-Gerlach tenía como objetivo probar la hipótesis de Bohr-Sommerfeld de que la dirección del momento angular de un átomo de plata está cuantizada. [14]
El experimento se realizó primero con un electroimán que permitía que el campo magnético no uniforme se activara gradualmente a partir de un valor nulo. [1] Cuando el campo era nulo, los átomos de plata se depositaban como una sola banda en el portaobjetos de vidrio detector. Cuando el campo se hizo más fuerte, la mitad de la banda comenzó a ensancharse y finalmente a dividirse en dos, de modo que la imagen del portaobjetos de vidrio parecía una huella de labios, con una abertura en el medio y un cierre en cada extremo. [15] En el medio, donde el campo magnético era lo suficientemente fuerte como para dividir el haz en dos, estadísticamente la mitad de los átomos de plata habían sido desviados por la no uniformidad del campo.
Cabe señalar que el experimento se realizó varios años antes de que George Uhlenbeck y Samuel Goudsmit formularan su hipótesis sobre la existencia del espín del electrón en 1925. [16] Aunque el resultado del experimento de Stern-Gerlach resultó posteriormente estar de acuerdo con las predicciones de la mecánica cuántica para una partícula de espín 1/2, el resultado experimental también fue consistente con la teoría de Bohr-Sommerfeld . [17]
En 1927, TE Phipps y JB Taylor reprodujeron el efecto utilizando átomos de hidrógeno en su estado fundamental , eliminando así cualquier duda que pudiera haber sido causada por el uso de átomos de plata . [18] Sin embargo, en 1926 la ecuación escalar no relativista de Schrödinger había predicho incorrectamente que el momento magnético del hidrógeno era cero en su estado fundamental. Para corregir este problema, Wolfgang Pauli consideró una versión de espín 1/2 de la ecuación de Schrödinger utilizando las 3 matrices de Pauli que ahora llevan su nombre, que luego Paul Dirac demostró en 1928 que era una consecuencia de su ecuación de Dirac relativista .
A principios de la década de 1930, Stern, junto con Otto Robert Frisch e Immanuel Estermann, mejoraron el aparato de haz molecular lo suficiente como para medir el momento magnético del protón , un valor casi 2000 veces menor que el momento del electrón. En 1931, el análisis teórico de Gregory Breit e Isidor Isaac Rabi demostró que este aparato podía usarse para medir el espín nuclear siempre que se conociera la configuración electrónica del átomo. El concepto fue aplicado por Rabi y Victor W. Cohen en 1934 para determinar el espín de los átomos de sodio . [19]
En 1938, Rabi y sus colaboradores insertaron un elemento de campo magnético oscilante en su aparato, inventando así la espectroscopia de resonancia magnética nuclear . [20] [21] Al ajustar la frecuencia del oscilador a la frecuencia de las precesiones nucleares, pudieron sintonizar selectivamente cada nivel cuántico del material en estudio. Rabi recibió el Premio Nobel en 1944 por este trabajo. [22]
Importancia
El experimento de Stern-Gerlach fue la primera evidencia directa de la cuantificación del momento angular en la mecánica cuántica, [23] e influyó fuertemente en los desarrollos posteriores en la física moderna :
- En la década siguiente, los científicos demostraron, utilizando técnicas similares, que los núcleos de algunos átomos también tienen un momento angular cuantificado. [20] Es la interacción de este momento angular nuclear con el espín del electrón lo que es responsable de la estructura hiperfina de las líneas espectroscópicas. [24]
- Norman F. Ramsey modificó posteriormente el aparato de Rabi para mejorar su sensibilidad (utilizando el método de campo oscilatorio separado ). [25] A principios de los años sesenta, Ramsey, H. Mark Goldenberg y Daniel Kleppner utilizaron un sistema Stern-Gerlach para producir un haz de hidrógeno polarizado como fuente de energía para el máser de hidrógeno . [26] Esto condujo al desarrollo de un reloj extremadamente estable basado en un máser de hidrógeno. Desde 1967 hasta 2019, el segundo se definió basándose en la transición hiperfina de 9.192.631.770 Hz de un átomo de cesio-133 ; el reloj atómico que se utiliza para establecer este estándar es una aplicación del trabajo de Ramsey. [27]
- El experimento de Stern-Gerlach se ha convertido en un prototipo de la medición cuántica , demostrando la observación de un único valor real ( valor propio ) de una propiedad física previamente indeterminada. [28] [29] [30] Al entrar en el imán de Stern-Gerlach, la dirección del momento magnético del átomo de plata es indefinida, pero cuando el átomo se registra en la pantalla, se observa que está en un punto o en el otro, y este resultado no se puede predecir de antemano. Debido a que el experimento ilustra el carácter de las mediciones cuánticas, las Conferencias Feynman sobre Física utilizan aparatos Stern-Gerlach idealizados para explicar las matemáticas básicas de la teoría cuántica. [31] [32] [33]
Véase también
Referencias
- ^ abc Gerlach, W .; Popa, O. (1922). "Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld" [La prueba experimental de la cuantificación direccional en el campo magnético]. Zeitschrift für Physik . 9 (1): 349–352. Código Bib : 1922ZPhy....9..349G. doi :10.1007/BF01326983. S2CID 186228677.
- ^ Franklin, Allan; Perovic, Slobodan. "Experimento en Física, Apéndice 5". En Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (edición de invierno de 2016) . Consultado el 14 de agosto de 2018 .
- ^ Friedrich, B.; Herschbach, D. (2003). "Stern y Gerlach: cómo un cigarro malo ayudó a reorientar la física atómica". Physics Today . 56 (12): 53. Bibcode :2003PhT....56l..53F. doi : 10.1063/1.1650229 . S2CID 17572089.
- ^ Castelvecchi, D. (2022). "El experimento de Stern-Gerlach a los 100". Nature Reviews Physics . 4 (3): 140–142. Código Bibliográfico :2022NatRP...4..140C. doi :10.1038/s42254-022-00436-4. S2CID 247184330.
- ^ Gerlach, W.; Popa, O. (1922). "Das magnetische Moment des Silberatoms" [El momento magnético del átomo de plata]. Zeitschrift für Physik . 9 (1): 353–355. Código Bib : 1922ZPhy....9..353G. doi :10.1007/BF01326984. S2CID 126109346.
- ^ Gerlach, W.; Popa, O. (1922). "Der experimentelle Nachweis des magnetischen Moments des Silberatoms" [La prueba experimental del momento magnético del átomo de plata]. Zeitschrift für Physik . 8 (1): 110–111. Código Bib : 1922ZPhy....8..110G. doi :10.1007/BF01329580. S2CID 122648402.
- ^ Mott, NF , Massey, HSW (1965/1971). The Theory of Atomic Collisions , tercera edición, Oxford University Press, Oxford, Reino Unido, págs. 214-219, §2, cap. IX, reimpreso en Wheeler, JA ; Zurek, WH (1983). Quantum Theory and Measurement . Princeton, NJ: Princeton University Press. págs. 701-706.
- ^ Rutherford, George H.; Grobe, Rainer (1997). "Comentario sobre el "efecto Stern-Gerlach para haces de electrones"". Phys. Rev. Lett . 81 (4772): 4772. Código Bibliográfico :1998PhRvL..81.4772R. doi :10.1103/PhysRevLett.81.4772.
- ^ Peres, Asher (1993). Teoría cuántica: conceptos y métodos . Kluwer . Págs. 14-18. ISBN. 0-7923-2549-4.
- ^ ab Sakurai, J.-J. (1985). Mecánica cuántica moderna . Addison-Wesley . ISBN 0-201-53929-2.
- ^ abc Qinxun, Li (8 de junio de 2020). «Experimento de Stern Gerlach: descripciones y desarrollos». Universidad de Ciencia y Tecnología de China : 2–5 . Consultado el 24 de noviembre de 2020 .
- ^ Castelvecchi, Davide (2020). "Un momento". Nature Physics . 16 (9): 994. Bibcode :2020NatPh..16..994C. doi :10.1038/s41567-020-1022-6. S2CID 225215678.
- ^ Kragh, Helge (2012). "La teoría de Bohr-Sommerfeld". Niels Bohr y el átomo cuántico: El modelo de Bohr de la estructura atómica 1913-1925. Oxford University Press. págs. 140-181. doi :10.1093/acprof:oso/9780199654987.003.0004. ISBN . 978-0-19-965498-7.
- ^ Popa, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld" [Una forma de probar experimentalmente la cuantificación direccional en un campo magnético]. Zeitschrift für Physik . 7 (1): 249–253. Código bibliográfico : 1921ZPhy....7..249S. doi :10.1007/BF01332793. S2CID 186234469.
- ^ French, AP , Taylor, EF (1979). Introducción a la física cuántica , Van Nostrand Reinhold, Londres, ISBN 0-442-30770-5 , págs. 428–442.
- ^ Eisberg, Robert; Resnick, Robert (1985). Física cuántica de átomos, moléculas, sólidos, núcleos y partículas (2.ª ed.). Wiley. pág. 277. ISBN 9780471873730.
- ^ Weinert, F. (1995). "Teoría errónea, experimento correcto: la importancia de los experimentos de Stern-Gerlach". Estudios de historia y filosofía de la física moderna . 26B (1): 75–86. Bibcode :1995SHPMP..26...75W. doi :10.1016/1355-2198(95)00002-B.
- ^ Phipps, TE; Taylor, JB (1927). "El momento magnético del átomo de hidrógeno". Physical Review . 29 (2): 309–320. Código Bibliográfico :1927PhRv...29..309P. doi :10.1103/PhysRev.29.309.
- ^ Kellogg, JBM; Millman, S. (1 de julio de 1946). "El método de resonancia magnética de haz molecular. Los espectros de radiofrecuencia de átomos y moléculas". Reseñas de física moderna . 18 (3): 323–352. doi :10.1103/RevModPhys.18.323. ISSN 0034-6861.
- ^ ab Rabi, II; Zacharias, JR; Millman, S. y Kusch, P. (1938). "Un nuevo método para medir el momento magnético nuclear". Physical Review . 53 (4): 318–327. Bibcode :1938PhRv...53..318R. doi : 10.1103/PhysRev.53.318 .
- ^ Hamilton, Donald R. (1941-12-01). "Haces moleculares y momentos nucleares". American Journal of Physics . 9 (6): 319–337. doi :10.1119/1.1991712. ISSN 0002-9505.
- ^ "El Premio Nobel de Física de 1944". NobelPrize.org .
- ^ Johnston, Hamish (1 de diciembre de 2022). «100 años del experimento de Stern-Gerlach». Physics World . 35 (12): 27–30. doi :10.1088/2058-7058/35/12/30. ISSN 0953-8585.
- ^ Griffiths, David (2005). Introducción a la mecánica cuántica (2.ª ed.). Pearson Prentice Hall . pág. 267. ISBN 0-13-111892-7.
- ^ "Norman F. Ramsey – Autobiografía". The Nobel Foundation . Consultado el 13 de junio de 2013 .
- ^ Ramsey, Norman F. (1968). "El máser de hidrógeno atómico". Científico estadounidense . 56 (4): 420–438. ISSN 0003-0996. JSTOR 27828332.
- ^ "Nobel Prize press release". The Nobel Foundation . Consultado el 13 de junio de 2013 .
- ^ Bohm, David (1951). Teoría cuántica . Nueva York: Prentice-Hall. pp. 326–330.
- ^ Gottfried, Kurt (1966). Mecánica cuántica . Nueva York: WA Benjamin, Inc., págs. 170-174.
- ^ Eisberg, Robert (1961). Fundamentos de la Física Moderna . Nueva York: John Wiley & Sons. págs. 334–338. ISBN 0-471-23463-X.
- ^ Feynman, Richard P. ; Leighton, Robert B. ; Sands, Matthew L. (2006) [1966]. "5. Spin One". Las conferencias Feynman sobre física . Vol. 3 (edición definitiva). San Francisco, California: Pearson Addison Wesley. ISBN 978-0-8053-9045-2.
- ^ Gale, W.; Guth, E.; Trammell, GT (25 de enero de 1968). "Determinación del estado cuántico mediante mediciones". Physical Review . 165 (5): 1434–1436. doi :10.1103/PhysRev.165.1434.
- ^ Ududec, Cozmin; Barnum, Howard; Emerson, Joseph (marzo de 2011). "Experimentos de tres rendijas y la estructura de la teoría cuántica". Fundamentos de la física . 41 (3): 396–405. arXiv : 0909.4787 . Código Bibliográfico :2011FoPh...41..396U. doi :10.1007/s10701-010-9429-z.
Lectura adicional
- Hsu, B.; Berrondo, M.; Van Huele, J.-F. (2011). "Dinámica de Stern-Gerlach con propagadores cuánticos". Physical Review A . 83 (1): 012109–1–12. Código Bibliográfico :2011PhRvA..83a2109H. doi :10.1103/PhysRevA.83.012109.
- Margalit, Yair; Zhou, Zhifan; Machluf, Shimon; Japha, Yonathan; Moukouri, Samuel; Folman, Ron (23 de julio de 2019). "Análisis de un interferómetro de franja espacial de Stern-Gerlach de alta estabilidad". New Journal of Physics . 21 (7): 073040. Bibcode :2019NJPh...21g3040M. doi : 10.1088/1367-2630/ab2fdc .
- Reinisch, G. (1999). "El experimento de Stern-Gerlach como prueba de entrelazamiento cuántico pionera (y probablemente la más simple)". Physics Letters A . 259 (6): 427–430. Bibcode :1999PhLA..259..427R. doi :10.1016/S0375-9601(99)00472-7.
- Savitsky, Zack (5 de diciembre de 2023). "El experimento (a menudo) pasado por alto que reveló el mundo cuántico". Revista Quanta .
- Venugopalan, A. (1997). "Decoherencia y estados de gato de Schrödinger en un experimento de tipo Stern−Gerlach". Physical Review A . 56 (5): 4307–4310. Bibcode :1997PhRvA..56.4307V. doi :10.1103/PhysRevA.56.4307.
- Zwiebach, Barton (2022). "12.2: El experimento de Stern-Gerlach". Dominar la mecánica cuántica: conceptos básicos, teoría y aplicaciones . Prensa del MIT. ISBN 978-0-262-04613-8.
Enlaces externos
- Animación de subprograma Java del experimento Stern-Gerlach
- Modelo Flash del experimento de Stern-Gerlach
- Explicación detallada del experimento de Stern-Gerlach
- Animación, aplicaciones e investigaciones relacionadas con el spin (Université Paris Sud)
- Mecánica ondulatoria y experimento de Stern-Gerlach en el MIT OpenCourseWare

















