Experimento de doble rendija

En la física moderna , el experimento de la doble rendija demuestra que la luz y la materia pueden exhibir el comportamiento tanto de partículas clásicas como de ondas clásicas . Esta ambigüedad se considera evidencia de la naturaleza fundamentalmente probabilística de la mecánica cuántica . Este tipo de experimento fue realizado por primera vez por Thomas Young en 1801, como una demostración del comportamiento ondulatorio de la luz visible. ^[1] En 1927, Davisson y Germer e, independientemente, George Paget Thomson y su estudiante de investigación Alexander Reid ^[2] demostraron que los electrones muestran el mismo comportamiento, que luego se extendió a los átomos y las moléculas. ^{[3] [4] [5]} El experimento de Thomas Young con la luz fue parte de la física clásica mucho antes del desarrollo de la mecánica cuántica y el concepto de dualidad onda-partícula . Creía que demostraba que la teoría ondulatoria de la luz de Christiaan Huygens era correcta, y su experimento a veces se conoce como el experimento de Young ^[6] o las rendijas de Young. ^[7]

El experimento pertenece a una clase general de experimentos de "doble trayectoria", en los que una onda se divide en dos ondas separadas (la onda generalmente está formada por muchos fotones y es mejor denominarla frente de onda, para no confundirla con las propiedades de onda del fotón individual) que luego se combinan en una sola onda. Los cambios en las longitudes de trayectoria de ambas ondas dan como resultado un cambio de fase , creando un patrón de interferencia . Otra versión es el interferómetro de Mach-Zehnder , que divide el haz con un divisor de haz .

Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Número cuántico Estado Superposición Simetría Túnel Incertidumbre Función de onda Colapsar
Experimentos Desigualdad de Bell Desigualdad de CHSH Davisson-Germer Doble rendija Elitzur–Vaidman Franck-Hertz Desigualdad de Leggett Desigualdad de Leggett-Garg Mach–Zehnder Corchete Borrador cuántico Elección retrasada El gato de Schrödinger Stern-Gerlach La elección retrasada de Wheeler
Formulaciones Descripción general Heisenberg Interacción Matriz Espacio de fases Schrödinger Suma de historias (integral de trayectoria)
Ecuaciones Dirac Klein-Gordon Pablo Rydberg Schrödinger
Interpretaciones Bayesiano Historias consistentes Copenhague de Broglie–Bohm Conjunto Variable oculta Local Superdeterminismo Muchos mundos Colapso objetivo Lógica cuántica Relacional Transaccional De von Neumann-Wigner
Temas avanzados Mecánica cuántica relativista Teoría cuántica de campos Ciencia de la información cuántica Computación cuántica Caos cuántico Paradoja del EPR Matriz de densidad Teoría de la dispersión Mecánica estadística cuántica Aprendizaje automático cuántico
Científicos Aharonov Campana Bethe Negro Bloqueo Bóhm Bohr Nacido Bosé de Broglie Compton Dirac Davison Débye Fiesta de los testigos Einstein Everett Follar Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordán Kramer Cordero Landó Laue Mosley Millikan Onnas Pablo Planck Rabí Rama Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

En la versión básica de este experimento, una fuente de luz coherente , como un rayo láser , ilumina una placa perforada por dos rendijas paralelas, y la luz que pasa a través de las rendijas se observa en una pantalla detrás de la placa. ^{[8] [9]} La naturaleza ondulatoria de la luz hace que las ondas de luz que pasan a través de las dos rendijas interfieran , produciendo bandas brillantes y oscuras en la pantalla, un resultado que no se esperaría si la luz consistiera en partículas clásicas. ^{[8] [10]} Sin embargo, siempre se encuentra que la luz se absorbe en la pantalla en puntos discretos, como partículas individuales (no ondas); el patrón de interferencia aparece a través de la densidad variable de estas partículas que golpean la pantalla. ^[11] Además, las versiones del experimento que incluyen detectores en las rendijas encuentran que cada fotón detectado pasa a través de una rendija (como lo haría una partícula clásica), y no a través de ambas rendijas (como lo haría una onda). ^{[12] [13] [14] [15] [16]} Sin embargo, estos experimentos demuestran que las partículas no forman el patrón de interferencia si se detecta por qué rendija pasan. Estos resultados demuestran el principio de dualidad onda-partícula . ^{[17] [18]}

Se ha descubierto que otras entidades a escala atómica, como los electrones , exhiben el mismo comportamiento cuando se disparan hacia una rendija doble. ^[9] Además, se observa que la detección de impactos discretos individuales es inherentemente probabilística, lo que es inexplicable utilizando la mecánica clásica . ^[9]

El experimento puede realizarse con entidades mucho más grandes que los electrones y los fotones, aunque se vuelve más difícil a medida que aumenta el tamaño. Las entidades más grandes para las que se ha realizado el experimento de doble rendija fueron moléculas que comprendían cada una 2000 átomos (cuya masa total era de 25 000 unidades de masa atómica ). ^[19]

El experimento de la doble rendija (y sus variantes) se ha convertido en un clásico por su claridad a la hora de expresar los enigmas centrales de la mecánica cuántica. Richard Feynman lo llamó "un fenómeno que es imposible [...] de explicar de cualquier manera clásica , y que contiene en sí el corazón de la mecánica cuántica. En realidad, contiene el único misterio [de la mecánica cuántica]". ^[9]

Si la luz estuviera formada estrictamente por partículas ordinarias o clásicas , y se las lanzara en línea recta a través de una rendija y se las dejara chocar contra una pantalla situada al otro lado, esperaríamos ver un patrón correspondiente al tamaño y la forma de la rendija. Sin embargo, cuando se lleva a cabo realmente este "experimento de una sola rendija", el patrón que aparece en la pantalla es un patrón de difracción en el que la luz se dispersa. Cuanto más pequeña sea la rendija, mayor será el ángulo de dispersión. La parte superior de la imagen muestra la parte central del patrón que se forma cuando un láser rojo ilumina una rendija y, si se observa con atención, dos bandas laterales débiles. Se pueden ver más bandas con un aparato más refinado. La difracción explica el patrón como resultado de la interferencia de las ondas de luz procedentes de la rendija.

Si se iluminan dos rendijas paralelas, la luz procedente de las dos rendijas vuelve a interferir. En este caso, la interferencia es un patrón más pronunciado con una serie de bandas alternas de luz y oscuridad. El ancho de las bandas es una propiedad de la frecuencia de la luz que ilumina. ^[20] (Véase la fotografía inferior a la derecha.)

Cuando Thomas Young (1773-1829) demostró por primera vez este fenómeno, indicó que la luz consiste en ondas, ya que la distribución del brillo puede explicarse por la interferencia alternativamente aditiva y sustractiva de los frentes de onda . ^[9] El experimento de Young, realizado a principios del siglo XIX, jugó un papel crucial en la comprensión de la teoría ondulatoria de la luz, derrotando la teoría corpuscular de la luz propuesta por Isaac Newton , que había sido el modelo aceptado de propagación de la luz en los siglos XVII y XVIII.

Sin embargo, el descubrimiento posterior del efecto fotoeléctrico demostró que, en diferentes circunstancias, la luz puede comportarse como si estuviera compuesta de partículas discretas. Estos descubrimientos aparentemente contradictorios hicieron necesario ir más allá de la física clásica y tener en cuenta la naturaleza cuántica de la luz.

A Feynman le gustaba decir que toda la mecánica cuántica se puede extraer de una reflexión cuidadosa sobre las implicaciones de este único experimento. ^[21] También propuso (como experimento mental) que si se colocaban detectores delante de cada rendija, el patrón de interferencia desaparecería. ^[22]

La relación de dualidad Englert-Greenberger proporciona un tratamiento detallado de las matemáticas de la interferencia de doble rendija en el contexto de la mecánica cuántica.

En 1909, GI Taylor realizó por primera vez un experimento de doble rendija de baja intensidad ^[23] , reduciendo el nivel de luz incidente hasta que los eventos de emisión/absorción de fotones en su mayoría no se superpusieran.No se realizó ningún experimento de interferencia de rendija con nada que no fuera luz hasta 1961, cuando Claus Jönsson de la Universidad de Tübingen lo realizó con haces de electrones coherentes y múltiples rendijas. ^{[24] [25]} En 1974, los físicos italianos Pier Giorgio Merli, Gian Franco Missiroli y Giulio Pozzi realizaron un experimento relacionado utilizando electrones individuales de una fuente coherente y un divisor de haz de biprisma, mostrando la naturaleza estadística de la acumulación del patrón de interferencia, como predijo la teoría cuántica. ^{[26] [27]} En 2002, la versión de un solo electrón del experimento fue votada como "el experimento más hermoso" por los lectores de Physics World . ^[28] Desde entonces se han publicado varios experimentos relacionados, con un poco de controversia. ^[29]

En 2012, Stefano Frabboni y sus colaboradores enviaron electrones individuales a rendijas nanofabricadas (de unos 100 nm de ancho) y, al detectar los electrones transmitidos con un detector de un solo electrón, pudieron mostrar la acumulación de un patrón de interferencia de doble rendija. ^[30] Se han realizado muchos experimentos relacionados que involucran la interferencia coherente; son la base de la difracción de electrones moderna, la microscopía y la obtención de imágenes de alta resolución. ^{[31] [32]}

En 2018, se demostró la interferencia de partículas individuales para la antimateria en el Laboratorio de Positrones (L-NESS, Politecnico di Milano ) de Rafael Ferragut en Como ( Italia ), por un grupo dirigido por Marco Giammarchi. ^[33]

Una versión importante de este experimento implica la detección de partículas individuales. Al iluminar la doble rendija con una intensidad baja, las partículas individuales se detectan como puntos blancos en la pantalla. Sin embargo, curiosamente, surge un patrón de interferencia cuando se permite que estas partículas se acumulen una a una (ver la imagen siguiente).

Esto demuestra la dualidad onda-partícula , que establece que toda la materia exhibe propiedades tanto de onda como de partícula: la partícula se mide como un solo pulso en una sola posición, mientras que el módulo al cuadrado de la onda describe la probabilidad de detectar la partícula en un lugar específico en la pantalla dando un patrón de interferencia estadística. ^[35] Se ha demostrado que este fenómeno ocurre con fotones, ^[36] electrones, ^[37] átomos e incluso algunas moléculas: con buckminsterfullereno ( C
₆₀) en 2001, ^{[38] [39] [40] [41]} con 2 moléculas de 430 átomos ( C
₆₀(DO
₁₂F
₂₅)
₁₀y C
₁₆₈yo
₉₄F
₁₅₂Oh
₈norte
₄S
₄) en 2011, ^[42] y con moléculas de hasta 2000 átomos en 2019. ^[43] Además de los patrones de interferencia creados a partir de partículas individuales, hasta 4 fotones entrelazados también pueden mostrar patrones de interferencia. ^[44]

El interferómetro de Mach-Zehnder puede considerarse una versión simplificada del experimento de la doble rendija. En lugar de propagarse a través del espacio libre después de las dos rendijas y alcanzar cualquier posición en una pantalla extendida, en el interferómetro los fotones solo pueden propagarse a través de dos caminos y alcanzar dos fotodetectores discretos. Esto permite describirlo mediante álgebra lineal simple en dimensión 2, en lugar de ecuaciones diferenciales.

Un fotón emitido por el láser incide en el primer divisor de haz y se encuentra entonces en una superposición entre los dos caminos posibles. En el segundo divisor de haz estos caminos interfieren, haciendo que el fotón incida en el fotodetector de la derecha con probabilidad 1, y en el fotodetector de abajo con probabilidad 0. Es interesante considerar qué sucedería si el fotón estuviera definitivamente en cualquiera de los caminos entre los divisores de haz. Esto se puede lograr bloqueando uno de los caminos, o equivalentemente detectando la presencia de un fotón allí. En ambos casos ya no habrá interferencia entre los caminos, y ambos fotodetectores serán incididos con probabilidad 1/2. De esto podemos concluir que el fotón no toma un camino u otro después del primer divisor de haz, sino que está en una genuina superposición cuántica de los dos caminos. ^[45]

Un conocido experimento mental predice que si se colocan detectores de partículas en las rendijas, mostrando por cuál rendija pasa un fotón, el patrón de interferencia desaparecerá. ^[9] Este experimento de en qué dirección ilustra el principio de complementariedad de que los fotones pueden comportarse como partículas u ondas, pero no pueden observarse como ambos al mismo tiempo. ^{[46] [47] [48]} A pesar de la importancia de este experimento mental en la historia de la mecánica cuántica (por ejemplo, ver la discusión sobre la versión de Einstein de este experimento ), no se propusieron realizaciones técnicamente factibles de este experimento hasta la década de 1970. ^[49] (Las implementaciones ingenuas del experimento mental del libro de texto no son posibles porque los fotones no pueden detectarse sin absorber el fotón). Actualmente, se han realizado múltiples experimentos que ilustran varios aspectos de la complementariedad. ^[50]

Un experimento realizado en 1987 ^{[51] [52]} produjo resultados que demostraron que se podía obtener información parcial sobre el camino que había tomado una partícula sin destruir por completo la interferencia. Este "compromiso onda-partícula" toma la forma de una desigualdad que relaciona la visibilidad del patrón de interferencia y la distinguibilidad de los caminos en esa dirección. ^[53]

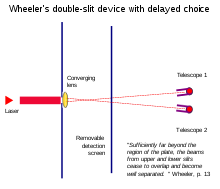
Los experimentos de elección retardada de Wheeler demuestran que extraer información sobre "qué camino seguir" después de que una partícula pasa por las rendijas puede parecer que altera retroactivamente su comportamiento previo en las rendijas.

Los experimentos con borradores cuánticos demuestran que el comportamiento de las ondas se puede restaurar borrando o haciendo que la información de "cuál camino" no esté disponible de forma permanente.

En un artículo de Scientific American se presentó una ilustración sencilla y casera del fenómeno del borrador cuántico . ^[54] Si se colocan polarizadores antes de cada rendija con sus ejes ortogonales entre sí, se eliminará el patrón de interferencia. Se puede considerar que los polarizadores introducen información sobre la trayectoria a seguir en cada haz. La introducción de un tercer polarizador frente al detector con un eje de 45° en relación con los otros polarizadores "borra" esta información, lo que permite que reaparezca el patrón de interferencia. Esto también se puede explicar considerando que la luz es una onda clásica, ^{[54] : 91} y también cuando se utilizan polarizadores circulares y fotones individuales. ^{[55] : 6} Las implementaciones de los polarizadores que utilizan pares de fotones entrelazados no tienen una explicación clásica. ^[55]

En un experimento muy publicitado en 2012, los investigadores afirmaron haber identificado el camino que había tomado cada partícula sin ningún efecto adverso en el patrón de interferencia generado por las partículas. ^[56] Para ello, utilizaron una configuración tal que las partículas que llegaban a la pantalla no provenían de una fuente puntual, sino de una fuente con dos máximos de intensidad. Sin embargo, comentaristas como Svensson ^[57] han señalado que, de hecho, no hay ningún conflicto entre las mediciones débiles realizadas en esta variante del experimento de doble rendija y el principio de incertidumbre de Heisenberg . La medición débil seguida de la selección posterior no permitió mediciones simultáneas de la posición y el momento de cada partícula individual, sino que permitió la medición de la trayectoria promedio de las partículas que llegaron a diferentes posiciones. En otras palabras, los experimentadores estaban creando un mapa estadístico del paisaje de trayectoria completo. ^[57]

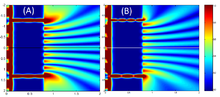
En 1967, Pfleegor y Mandel demostraron la interferencia de dos fuentes utilizando dos láseres separados como fuentes de luz. ^{[58] [59]}

En 1972 se demostró experimentalmente que en un sistema de doble rendija donde solo una rendija estaba abierta en cualquier momento, se observaba interferencia de todos modos siempre que la diferencia de trayectoria fuera tal que el fotón detectado pudiera haber venido de cualquiera de las rendijas. ^{[60] [61]} Las condiciones experimentales eran tales que la densidad de fotones en el sistema era mucho menor que 1.

En 1991, Carnal y Mlynek realizaron el clásico experimento de doble rendija de Young con átomos de helio metaestables que pasaban a través de rendijas de escala micrométrica en una lámina de oro. ^{[62] [63]}

En 1999, se realizó con éxito un experimento de interferencia cuántica (utilizando una rejilla de difracción, en lugar de dos rendijas) con moléculas de buckyball (cada una de las cuales comprende 60 átomos de carbono). ^{[38] [64]} Una buckyball es lo suficientemente grande (diámetro de aproximadamente 0,7  nm , casi medio millón de veces más grande que un protón) para ser vista en un microscopio electrónico .

En 2002, se utilizó una fuente de emisión de campo electrónico para demostrar el experimento de doble rendija. En este experimento, se emitió una onda electrónica coherente desde dos sitios de emisión ubicados muy cerca en el ápice de la aguja, que actuaron como rendijas dobles, dividiendo la onda en dos ondas electrónicas coherentes en el vacío. Luego se pudo observar el patrón de interferencia entre las dos ondas electrónicas. ^[65] En 2017, los investigadores realizaron el experimento de doble rendija utilizando emisores de electrones de campo inducidos por luz. Con esta técnica, los sitios de emisión se pueden seleccionar ópticamente en una escala de diez nanómetros. Al desactivar selectivamente (cerrar) una de las dos emisiones (rendijas), los investigadores pudieron demostrar que el patrón de interferencia desapareció. ^[66]

En 2005, ER Eliel presentó un estudio experimental y teórico de la transmisión óptica de una pantalla metálica delgada perforada por dos rendijas de longitud de onda inferior, separadas por muchas longitudes de onda ópticas. Se demostró que la intensidad total del patrón de doble rendija de campo lejano se reduce o mejora en función de la longitud de onda del haz de luz incidente. ^[67]

En 2012, investigadores de la Universidad de Nebraska-Lincoln realizaron el experimento de doble rendija con electrones descrito por Richard Feynman , utilizando nuevos instrumentos que permitieron controlar la transmisión de las dos rendijas y monitorear los eventos de detección de un solo electrón. Los electrones fueron disparados por un cañón de electrones y pasaron a través de una o dos rendijas de 62 nm de ancho × 4 μm de alto. ^[68]

En 2013, se realizó con éxito un experimento de interferencia cuántica (utilizando rejillas de difracción, en lugar de dos rendijas) con moléculas que comprendían cada una 810 átomos (cuya masa total era de más de 10 000 unidades de masa atómica ). ^{[4] [5]} El récord se elevó a 2000 átomos (25 000 uma) en 2019. ^[19]

Se han desarrollado análogos hidrodinámicos que pueden recrear varios aspectos de los sistemas mecánicos cuánticos, incluida la interferencia de una sola partícula a través de una doble rendija. ^[69] Una gota de aceite de silicona, que rebota a lo largo de la superficie de un líquido, se autopropulsa a través de interacciones resonantes con su propio campo de ondas. La gota chapotea suavemente el líquido con cada rebote. Al mismo tiempo, las ondulaciones de rebotes anteriores afectan su curso. La interacción de la gota con sus propias ondulaciones, que forman lo que se conoce como una onda piloto , hace que muestre comportamientos que antes se creían peculiares de las partículas elementales, incluidos comportamientos que habitualmente se toman como evidencia de que las partículas elementales se propagan a través del espacio como ondas, sin ninguna ubicación específica, hasta que se miden. ^{[70] [71]}

Entre los comportamientos imitados a través de este sistema de onda piloto hidrodinámico se incluyen la difracción cuántica de partículas individuales, ^[72] efecto túnel, órbitas cuantificadas, división de niveles orbitales, espín y estadísticas multimodales. También es posible inferir relaciones de incertidumbre y principios de exclusión. Hay videos disponibles que ilustran varias características de este sistema. (Véase los enlaces externos).

Sin embargo, los sistemas más complicados que involucran dos o más partículas en superposición no son susceptibles de una explicación tan simple e intuitiva desde el punto de vista clásico. ^[73] En consecuencia, no se ha desarrollado ningún análogo hidrodinámico del entrelazamiento. ^[69] Sin embargo, son posibles análogos ópticos. ^[74]

En 2023, se informó de un experimento que recreaba un patrón de interferencia en el tiempo al hacer brillar un pulso láser de bombeo en una pantalla recubierta de óxido de indio y estaño (ITO) que alteraría las propiedades de los electrones dentro del material debido al efecto Kerr , cambiándolo de transparente a reflectante durante unos 200 femtosegundos de duración, donde un rayo láser de sonda posterior que golpeara la pantalla de ITO vería este cambio temporal en las propiedades ópticas como una rendija en el tiempo y dos de ellas como una rendija doble con una diferencia de fase que se suma destructivamente o constructivamente en cada componente de frecuencia, lo que resulta en un patrón de interferencia. ^{[75] [76] [77]} Se han obtenido resultados similares de forma clásica en ondas de agua. ^{[75] [77]}

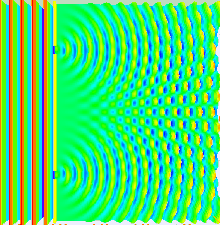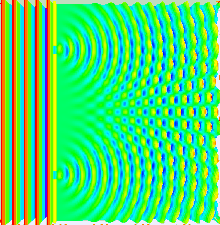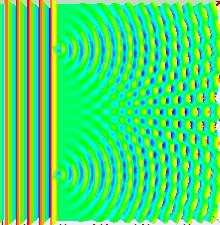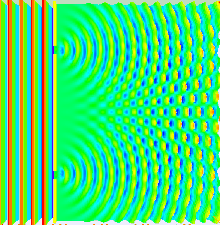
Gran parte del comportamiento de la luz se puede modelar utilizando la teoría ondulatoria clásica. El principio de Huygens-Fresnel es uno de esos modelos; establece que cada punto de un frente de onda genera una ondícula secundaria y que la perturbación en cualquier punto posterior se puede encontrar sumando las contribuciones de las ondículas individuales en ese punto. Esta suma debe tener en cuenta la fase , así como la amplitud de las ondículas individuales. Solo se puede medir la intensidad de un campo de luz, que es proporcional al cuadrado de la amplitud.

En el experimento de la doble rendija, las dos rendijas se iluminan con la luz cuasi monocromática de un único láser. Si el ancho de las rendijas es lo suficientemente pequeño (mucho menor que la longitud de onda de la luz láser), las rendijas difractan la luz en ondas cilíndricas. Estos dos frentes de onda cilíndricos se superponen y la amplitud, y por lo tanto la intensidad, en cualquier punto de los frentes de onda combinados depende tanto de la magnitud como de la fase de los dos frentes de onda. La diferencia de fase entre las dos ondas está determinada por la diferencia en la distancia recorrida por las dos ondas.

Si la distancia de observación es grande en comparación con la separación de las rendijas (el campo lejano ), la diferencia de fase se puede encontrar utilizando la geometría que se muestra en la figura de abajo a la derecha. La diferencia de trayectoria entre dos ondas que viajan en un ángulo θ se da por:

${\displaystyle d\sin \theta \approx d\theta }$

Donde d es la distancia entre las dos rendijas. Cuando las dos ondas están en fase, es decir, la diferencia de trayectoria es igual a un número entero de longitudes de onda, la amplitud sumada y, por lo tanto, la intensidad sumada es máxima, y ​​cuando están en antifase, es decir, la diferencia de trayectoria es igual a media longitud de onda, una longitud de onda y media, etc., entonces las dos ondas se cancelan y la intensidad sumada es cero. Este efecto se conoce como interferencia . Los máximos de la franja de interferencia se producen en ángulos

${\displaystyle ~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots }$

donde λ es la longitud de onda de la luz. El espaciamiento angular de las franjas, θ _f , está dado por

${\displaystyle \theta _{f}\approx \lambda /d}$

El espaciamiento de las franjas a una distancia z de las rendijas viene dado por

${\displaystyle ~w=z\theta _{f}=z\lambda /d}$

Por ejemplo, si dos rendijas están separadas por 0,5 mm ( d ), y se iluminan con un láser con una longitud de onda de 0,6 μm ( λ ), entonces a una distancia de 1 m ( z ), el espaciamiento de las franjas será de 1,2 mm.

Si el ancho de las rendijas b es apreciable en comparación con la longitud de onda, se necesita la ecuación de difracción de Fraunhofer para determinar la intensidad de la luz difractada de la siguiente manera: ^[78]

${\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}}$

donde la función sinc se define como sinc( x ) = sin( x )/ x para x ≠ 0, y sinc(0) = 1.

Esto se ilustra en la figura anterior, donde el primer patrón es el patrón de difracción de una sola rendija, dado por la función sinc en esta ecuación, y la segunda figura muestra la intensidad combinada de la luz difractada de las dos rendijas, donde la función cos representa la estructura fina y la estructura más gruesa representa la difracción de las rendijas individuales como lo describe la función sinc .

Se pueden realizar cálculos similares para el campo cercano aplicando la ecuación de difracción de Fresnel , que implica que a medida que el plano de observación se acerca al plano en el que se encuentran las rendijas, los patrones de difracción asociados con cada rendija disminuyen de tamaño, de modo que el área en la que se produce la interferencia se reduce y puede desaparecer por completo cuando no hay superposición en los dos patrones difractados. ^[79]

El experimento de la doble rendija puede ilustrar la formulación integral de trayectorias de la mecánica cuántica proporcionada por Feynman. ^[80] La formulación integral de trayectorias reemplaza la noción clásica de una trayectoria única para un sistema, con una suma de todas las trayectorias posibles. Las trayectorias se suman mediante el uso de la integración funcional .

Cada camino se considera igualmente probable y, por lo tanto, contribuye en la misma cantidad. Sin embargo, la fase de esta contribución en cualquier punto dado a lo largo del camino está determinada por la acción a lo largo del camino:$${\displaystyle A_{\text{path}}(x,y,z,t)=e^{iS(x,y,z,t)}}$$

Luego se suman todas estas contribuciones y se eleva al cuadrado la magnitud del resultado final para obtener la distribución de probabilidad de la posición de una partícula:$${\displaystyle p(x,y,z,t)\propto \left\vert \int _{\text{all paths}}e^{iS(x,y,z,t)}\right\vert ^{2}}$$

Como siempre ocurre al calcular la probabilidad , los resultados deben normalizarse imponiendo:$${\displaystyle \iiint _{\text{all space}}p(x,y,z,t)\,dV=1}$$

La distribución de probabilidad del resultado es el cuadrado normalizado de la norma de la superposición , sobre todos los caminos desde el punto de origen hasta el punto final, de ondas que se propagan proporcionalmente a la acción a lo largo de cada camino. Las diferencias en la acción acumulada a lo largo de los diferentes caminos (y por lo tanto las fases relativas de las contribuciones) producen el patrón de interferencia observado por el experimento de doble rendija. Feynman enfatizó que su formulación es meramente una descripción matemática, no un intento de describir un proceso real que podamos medir.

Al igual que el experimento mental del gato de Schrödinger , el experimento de la doble rendija se utiliza a menudo para resaltar las diferencias y similitudes entre las diversas interpretaciones de la mecánica cuántica .

La interpretación estándar del experimento de la doble rendija es que el patrón es un fenómeno ondulatorio que representa la interferencia entre dos amplitudes de probabilidad, una para cada rendija. Los experimentos de baja intensidad demuestran que el patrón se llena con la detección de una partícula a la vez. Cualquier cambio en el aparato diseñado para detectar una partícula en una rendija particular altera las amplitudes de probabilidad y la interferencia desaparece. ^{[50] : S298} Esta interpretación es independiente de cualquier observador consciente. ^{[81] :  S281}

Niels Bohr interpretó los experimentos cuánticos como el experimento de la doble rendija utilizando el concepto de complementariedad. ^[82] En la visión de Bohr, los sistemas cuánticos no son clásicos, pero las mediciones solo pueden dar resultados clásicos. Ciertos pares de propiedades clásicas nunca se observarán simultáneamente en un sistema cuántico: el patrón de interferencia de ondas en el experimento de la doble rendija desaparecerá si se detectan partículas en las rendijas. Las versiones modernas cuantitativas del concepto permiten un equilibrio continuo entre la visibilidad de las franjas de interferencia y la probabilidad de detección de partículas en una rendija. ^{[83] [84]}

La interpretación de Copenhague es una colección de puntos de vista sobre el significado de la mecánica cuántica , que se derivan del trabajo de Niels Bohr , Werner Heisenberg , Max Born y otros. El término "interpretación de Copenhague" fue aparentemente acuñado por Heisenberg durante la década de 1950 para referirse a las ideas desarrolladas en el período 1925-1927, pasando por alto sus desacuerdos con Bohr. ^{[82] [85] [86] [87]} En consecuencia, no hay una declaración histórica definitiva de lo que implica la interpretación. Las características comunes en todas las versiones de la interpretación de Copenhague incluyen la idea de que la mecánica cuántica es intrínsecamente indeterminista , con probabilidades calculadas utilizando la regla de Born y alguna forma de principio de complementariedad . ^{[88] : 41–54} Además, el acto de "observar" o "medir" un objeto es irreversible, y no se puede atribuir ninguna verdad a un objeto, excepto de acuerdo con los resultados de su medición . En la interpretación de Copenhague, la complementariedad significa que un experimento particular puede demostrar el comportamiento de una partícula (pasando a través de una rendija definida) o el comportamiento de una onda (interferencia), pero no ambos al mismo tiempo. ^{[88] :  49  [89] [90]} En una visión de tipo Copenhague, la cuestión de por qué rendija viaja una partícula no tiene sentido cuando no hay un detector. ^{[91] [92]}

Según la interpretación relacional de la mecánica cuántica , propuesta por primera vez por Carlo Rovelli , ^[93] las observaciones como las del experimento de la doble rendija resultan específicamente de la interacción entre el observador (dispositivo de medición) y el objeto observado (con el que se interactúa físicamente), no de ninguna propiedad absoluta que posea el objeto. En el caso de un electrón, si inicialmente se lo "observa" en una rendija particular, entonces la interacción observador-partícula (fotón-electrón) incluye información sobre la posición del electrón. Esto restringe parcialmente la ubicación final de la partícula en la pantalla. Si se lo "observa" (se mide con un fotón) no en una rendija particular sino en la pantalla, entonces no hay información sobre "qué camino" como parte de la interacción, por lo que la posición "observada" del electrón en la pantalla está determinada estrictamente por su función de probabilidad. Esto hace que el patrón resultante en la pantalla sea el mismo que si cada electrón individual hubiera pasado por ambas rendijas. ^{[ cita requerida ]}

Al igual que en el caso de Copenhague, existen múltiples variantes de la interpretación de los múltiples mundos . El tema unificador es que la realidad física se identifica con una función de onda, y esta función de onda siempre evoluciona unitariamente, es decir, siguiendo la ecuación de Schrödinger sin colapsos. ^{[94] [95]} En consecuencia, existen muchos universos paralelos, que solo interactúan entre sí a través de interferencias. David Deutsch sostiene que la forma de entender el experimento de la doble rendija es que en cada universo la partícula viaja a través de una rendija específica, pero su movimiento se ve afectado por la interferencia con partículas en otros universos. Esto crea las franjas observables. ^[96] David Wallace, otro defensor de la interpretación de los múltiples mundos, escribe que en la configuración familiar del experimento de la doble rendija los dos caminos no están suficientemente separados para que una descripción en términos de universos paralelos tenga sentido. ^[97]

La teoría de De Broglie-Bohm , una alternativa a la interpretación estándar de la mecánica cuántica, afirma que las partículas también tienen ubicaciones precisas en todo momento y que sus velocidades están definidas por la función de onda. De modo que, mientras que una única partícula viajará a través de una rendija particular en el experimento de doble rendija, la denominada "onda piloto" que la influye viajará a través de ambas. Las dos trayectorias de De Broglie-Bohm en la rendija fueron calculadas por primera vez por Chris Dewdney mientras trabajaba con Chris Philippidis y Basil Hiley en el Birkbeck College (Londres). ^[98] La teoría de De Broglie-Bohm produce los mismos resultados estadísticos que la mecánica cuántica estándar, pero elimina muchas de sus dificultades conceptuales al añadir complejidad mediante un potencial cuántico ad hoc para guiar las partículas. ^[99]

Si bien el modelo es en muchos aspectos similar a la ecuación de Schrödinger , se sabe que falla en los casos relativistas ^[100] y no tiene en cuenta características como la creación o aniquilación de partículas en la teoría cuántica de campos . Muchos autores, como los premios Nobel Werner Heisenberg ^[101] , Sir Anthony James Leggett ^[102] y Sir Roger Penrose ^[103], lo han criticado por no aportar nada nuevo.

Han aparecido variantes más complejas de este tipo de enfoque, por ejemplo la hipótesis de las tres ondas ^{[104] [105]} de Ryszard Horodecki , así como otras combinaciones complicadas de ondas de De Broglie y Compton. ^{[106] [107] [108]} Hasta la fecha no hay evidencia de que sean útiles.

• Al-Khalili, Jim (2003). Quantum: una guía para los perplejos . Londres: Weidenfeld & Nicolson. ISBN 978-0-297-84305-4.
• Ananthaswamy, Anil (2018). A través de dos puertas a la vez: el elegante experimento que captura el enigma de nuestra realidad cuántica . Dutton/Penguin. ISBN 978-1-101-98609-7.
• Feynman, Richard P. (1988). QED: La extraña teoría de la luz y la materia. Princeton University Press. ISBN 978-0-691-02417-2.
• Frank, Philipp (1957). Filosofía de la ciencia . Prentice-Hall.
• Francés, AP; Taylor, Edwin F. (1978). Introducción a la física cuántica . Norton. ISBN 978-0-393-09106-9.
• Greene, Brian (2000). El universo elegante . Vintage. ISBN 978-0-375-70811-4.
• Greene, Brian (2005). El tejido del cosmos . Vintage. ISBN 978-0-375-72720-7.
• Gribbin, John (1999). Q es de cuántica: física de partículas de la A a la Z. Weidenfeld & Nicolson. ISBN 978-0-7538-0685-2.
• Hola, Tony (2003). El nuevo universo cuántico . Cambridge University Press. Bibcode :2003nqu..book.....H. ISBN 978-0-521-56457-1.
• Sears, Francis Weston (1949). Óptica . Addison Wesley.
• Tipler, Paul (2004). Física para científicos e ingenieros: electricidad, magnetismo, luz y física moderna elemental (5.ª ed.). WH Freeman. ISBN 978-0-7167-0810-0.

Wikimedia Commons tiene medios relacionados con Experimentos de doble rendija .

• Conferencia sobre interferencia de doble rendija a cargo de Walter Lewin del MIT

• Huygens y la interferencia Archivado el 28 de octubre de 2007 en Wayback Machine.

• Sitio web con la película y otra información del primer experimento con un solo electrón de Merli, Missiroli y Pozzi.
• Película que muestra cómo los eventos de un solo electrón se acumulan para formar un patrón de interferencia en experimentos de doble rendija. Varias versiones con y sin narración (Tamaño del archivo = 3,6 a 10,4 MB) (Duración de la película = 1m 8s)
• Vídeo de Freeview 'Las ondas electrónicas revelan el microcosmos' Discurso de la Royal Institution a cargo de Akira Tonomura proporcionado por Vega Science Trust
• Sitio web de Hitachi que proporciona información sobre el video de Tonomura y un enlace al video

• "Se observa interferencia de partículas individuales en objetos macroscópicos"
• Hidrodinámica de ondas piloto: video complementario
• A través del agujero de gusano: Yves Couder explica la dualidad onda/partícula a través de gotitas de silicio

• Demostración en Java de la interferencia de la doble rendija de Young
• Una simulación que se ejecuta en Mathematica Player, en la que el número de partículas cuánticas, la frecuencia de las partículas y la separación de las rendijas se pueden variar de forma independiente.