Nivel de energía

Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Número cuántico Estado Superposición Simetría Túnel Incertidumbre Función de onda Colapsar
Experimentos Desigualdad de Bell Desigualdad de CHSH Davisson-Germer Doble rendija Elitzur–Vaidman Franck-Hertz Desigualdad de Leggett Desigualdad de Leggett-Garg Mach–Zehnder Corchete Borrador cuántico Elección retrasada El gato de Schrödinger Stern–Gerlach La elección retrasada de Wheeler
Formulaciones Descripción general Heisenberg Interacción Matriz Espacio de fases Schrödinger Suma de historias (integral de trayectoria)
Ecuaciones Dirac Klein-Gordon Pablo Rydberg Schrödinger
Interpretaciones Bayesiano Historias consistentes Copenhague de Broglie–Bohm Conjunto Variable oculta Local Superdeterminismo Muchos mundos Colapso objetivo Lógica cuántica Relacional Transaccional De von Neumann-Wigner
Temas avanzados Mecánica cuántica relativista Teoría cuántica de campos Ciencia de la información cuántica Computación cuántica Caos cuántico Paradoja del EPR Matriz de densidad Teoría de la dispersión Mecánica estadística cuántica Aprendizaje automático cuántico
Científicos Aharonov Campana Bethe Negro Bloqueo Bóhm Bohr Nacido Bosé de Broglie Compton Dirac Davison Debye Fiesta de los testigos Einstein Everett Follar Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordán Kramer Cordero Landó Laue Mosley Millikan Onnas Pablo Planck Rabí Rama Rydberg Schrödinger Simmons Campo de verano de Neumann Weyl Viena Wigner Zeeman Zeilinger
v t e

Un sistema o partícula mecánica cuántica que está ligado —es decir, confinado espacialmente— solo puede asumir ciertos valores discretos de energía, llamados niveles de energía . Esto contrasta con las partículas clásicas , que pueden tener cualquier cantidad de energía. El término se usa comúnmente para los niveles de energía de los electrones en átomos , iones o moléculas , que están ligados por el campo eléctrico del núcleo , pero también puede referirse a los niveles de energía de los núcleos o a los niveles de energía vibracional o rotacional en las moléculas. El espectro de energía de un sistema con tales niveles de energía discretos se dice que está cuantizado .

En química y física atómica , una capa de electrones, o nivel de energía principal, puede considerarse como la órbita de uno o más electrones alrededor del núcleo de un átomo . La capa más cercana al núcleo se denomina "capa 1" (también llamada "capa K"), seguida de la "capa 2" (o "capa L"), luego la "capa 3" (o "capa M"), y así sucesivamente alejándose cada vez más del núcleo. Las capas se corresponden con los números cuánticos principales ( n = 1, 2, 3, 4, ...) o se etiquetan alfabéticamente con letras utilizadas en la notación de rayos X (K, L, M, N, ...).

Cada capa puede contener sólo un número fijo de electrones: la primera capa puede contener hasta dos electrones, la segunda capa puede contener hasta ocho (2 + 6) electrones, la tercera capa puede contener hasta 18 (2 + 6 + 10) y así sucesivamente. La fórmula general es que la capa n puede, en principio, contener hasta 2 n ² electrones. ^[1] Dado que los electrones son atraídos eléctricamente hacia el núcleo, los electrones de un átomo generalmente ocuparán las capas externas sólo si las capas más internas ya han sido completamente llenas por otros electrones. Sin embargo, este no es un requisito estricto: los átomos pueden tener dos o incluso tres capas externas incompletas. (Véase la regla de Madelung para más detalles.) Para una explicación de por qué existen los electrones en estas capas, véase configuración electrónica . ^[2]

Si la energía potencial se establece en cero a una distancia infinita del núcleo atómico o la molécula, la convención habitual, entonces los estados de electrones ligados tienen energía potencial negativa.

Si un átomo, ion o molécula se encuentra en el nivel de energía más bajo posible, se dice que él y sus electrones están en el estado fundamental . Si se encuentra en un nivel de energía más alto, se dice que está excitado , o que están excitados todos los electrones que tienen una energía más alta que el estado fundamental . Un nivel de energía se considera degenerado si hay más de un estado mecánico cuántico medible asociado a él.

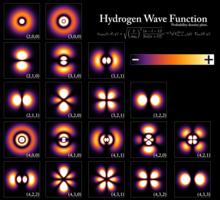
Los niveles de energía cuantizados resultan del comportamiento ondulatorio de las partículas, que da una relación entre la energía de una partícula y su longitud de onda . Para una partícula confinada como un electrón en un átomo , las funciones de onda que tienen energías bien definidas tienen la forma de una onda estacionaria . ^[3] Los estados que tienen energías bien definidas se denominan estados estacionarios porque son los estados que no cambian en el tiempo. De manera informal, estos estados corresponden a un número entero de longitudes de onda de la función de onda a lo largo de una trayectoria cerrada (una trayectoria que termina donde comenzó), como una órbita circular alrededor de un átomo, donde el número de longitudes de onda da el tipo de orbital atómico (0 para orbitales s, 1 para orbitales p, etc.). Ejemplos elementales que muestran matemáticamente cómo surgen los niveles de energía son la partícula en una caja y el oscilador armónico cuántico .

Cualquier superposición ( combinación lineal ) de estados de energía también es un estado cuántico, pero dichos estados cambian con el tiempo y no tienen energías bien definidas. Una medición de la energía da como resultado el colapso de la función de onda, lo que da como resultado un nuevo estado que consiste en un solo estado de energía. La medición de los posibles niveles de energía de un objeto se llama espectroscopia .

La primera evidencia de la cuantización en los átomos fue la observación de líneas espectrales en la luz del sol a principios del siglo XIX por parte de Joseph von Fraunhofer y William Hyde Wollaston . La noción de niveles de energía fue propuesta en 1913 por el físico danés Niels Bohr en la teoría de Bohr del átomo. La teoría mecánica cuántica moderna que ofrece una explicación de estos niveles de energía en términos de la ecuación de Schrödinger fue propuesta por Erwin Schrödinger y Werner Heisenberg en 1926.

En las fórmulas de energía de los electrones en los distintos niveles que se indican a continuación en un átomo, el punto cero de energía se establece cuando el electrón en cuestión ha abandonado completamente el átomo; es decir, cuando el número cuántico principal del electrón n = ∞ . Cuando el electrón está ligado al átomo en un valor más cercano de n , la energía del electrón es menor y se considera negativa.

Supongamos que hay un electrón en un orbital atómico determinado en un átomo (ion) similar al hidrógeno . La energía de su estado está determinada principalmente por la interacción electrostática del electrón (negativo) con el núcleo (positivo). Los niveles de energía de un electrón alrededor de un núcleo están dados por:

${\displaystyle E_{n}=-hcR_{\infty }{\frac {Z^{2}}{n^{2}}}}$

(normalmente entre 1  eV y 10 ³  eV), donde R _∞ es la constante de Rydberg , Z es el número atómico , n es el número cuántico principal , h es la constante de Planck y c es la velocidad de la luz . Solo para átomos similares al hidrógeno (iones), los niveles de Rydberg dependen únicamente del número cuántico principal n .

Esta ecuación se obtiene combinando la fórmula de Rydberg para cualquier elemento similar al hidrógeno (mostrado a continuación) con E = hν = hc  /  λ suponiendo que el número cuántico principal n anterior = n ₁ en la fórmula de Rydberg y n ₂ = ∞ (número cuántico principal del nivel de energía del que desciende el electrón, al emitir un fotón ). La fórmula de Rydberg se derivó de datos empíricos de emisión espectroscópica .

${\displaystyle {\frac {1}{\lambda }}=RZ^{2}\left({\frac {1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right)}$

Se puede derivar una fórmula equivalente desde la mecánica cuántica a partir de la ecuación de Schrödinger independiente del tiempo con un operador hamiltoniano de energía cinética utilizando una función de onda como función propia para obtener los niveles de energía como valores propios , pero la constante de Rydberg sería reemplazada por otras constantes de la física fundamental.

Si hay más de un electrón alrededor del átomo, las interacciones electrón-electrón aumentan el nivel de energía. Estas interacciones suelen pasarse por alto si la superposición espacial de las funciones de onda de los electrones es baja.

En el caso de los átomos con múltiples electrones, las interacciones entre electrones hacen que la ecuación anterior ya no sea precisa, tal como se indica simplemente con Z como el número atómico . Una forma sencilla (aunque no completa) de entender esto es como un efecto de protección , donde los electrones externos ven un núcleo efectivo de carga reducida, ya que los electrones internos están fuertemente unidos al núcleo y cancelan parcialmente su carga. Esto conduce a una corrección aproximada donde Z se sustituye por una carga nuclear efectiva simbolizada como Z _eff que depende en gran medida del número cuántico principal.$${\displaystyle E_{n,\ell }=-hcR_{\infty }{\frac {{Z_{\rm {eff}}}^{2}}{n^{2}}}}$$

En tales casos, los tipos de orbitales (determinados por el número cuántico azimutal ℓ ) así como sus niveles dentro de la molécula afectan a Z _eff y por lo tanto también afectan a los diversos niveles de energía de los electrones atómicos. El principio de Aufbau de llenar un átomo con electrones para una configuración electrónica tiene en cuenta estos diferentes niveles de energía. Para llenar un átomo con electrones en el estado fundamental , los niveles de energía más bajos se llenan primero y es consistente con el principio de exclusión de Pauli , el principio de Aufbau y la regla de Hund .

La estructura fina surge de las correcciones relativistas de la energía cinética, el acoplamiento espín-órbita (una interacción electrodinámica entre el espín y el movimiento del electrón y el campo eléctrico del núcleo) y el término de Darwin (término de contacto de la interacción de los electrones de la capa s ^{[ ¿cuál? ]} dentro del núcleo). Estos afectan los niveles en un orden de magnitud típico de 10 ⁻³  eV.

Esta estructura aún más fina se debe a la interacción espín-espín electrón-núcleo , que da como resultado un cambio típico en los niveles de energía de un orden de magnitud típico de 10 ⁻⁴  eV.

Hay una energía de interacción asociada con el momento dipolar magnético, μ _L , que surge del momento angular orbital electrónico, L , dado por

${\displaystyle U=-{\boldsymbol {\mu }}_{L}\cdot \mathbf {B} }$

con

${\displaystyle -{\boldsymbol {\mu }}_{L}={\dfrac {e\hbar }{2m}}\mathbf {L} =\mu _{B}\mathbf {L} }$.

Además, hay que tener en cuenta el momento magnético que surge del espín del electrón.

Debido a los efectos relativistas ( ecuación de Dirac ), existe un momento magnético, μ _S , que surge del espín del electrón.

${\displaystyle -{\boldsymbol {\mu }}_{S}=-\mu _{\text{B}}g_{S}\mathbf {S} }$,

con g _S el factor g del espín del electrón (aproximadamente 2), lo que da como resultado un momento magnético total, μ ,

${\displaystyle {\boldsymbol {\mu }}={\boldsymbol {\mu }}_{L}+{\boldsymbol {\mu }}_{S}}$.

Por lo tanto, la energía de interacción se convierte en

${\displaystyle U_{B}=-{\boldsymbol {\mu }}\cdot \mathbf {B} =\mu _{\text{B}}B(M_{L}+g_{S}M_{S})}$.

Los enlaces químicos entre átomos en una molécula se forman porque hacen que la situación sea más estable para los átomos involucrados, lo que generalmente significa que el nivel de energía total para los átomos involucrados en la molécula es menor que si los átomos no estuvieran unidos de esa manera. A medida que los átomos separados se aproximan entre sí para unirse covalentemente , sus orbitales afectan los niveles de energía de cada uno para formar orbitales moleculares de enlace y antienlace . El nivel de energía de los orbitales de enlace es menor y el nivel de energía de los orbitales antienlace es mayor. Para que el enlace en la molécula sea estable, los electrones de enlace covalente ocupan el orbital de enlace de menor energía, que puede estar representado por símbolos como σ o π según la situación. Los orbitales antienlazantes correspondientes pueden representarse agregando un asterisco para obtener orbitales σ* o π*. Un orbital no enlazante en una molécula es un orbital con electrones en capas externas que no participan en el enlace y su nivel de energía es el mismo que el del átomo constituyente. Estos orbitales pueden designarse como orbitales n . Los electrones en un orbital n son típicamente pares solitarios . ^[4] En las moléculas poliatómicas, también intervienen diferentes niveles de energía vibracional y rotacional.

En términos generales, un estado de energía molecular (es decir, un estado propio del hamiltoniano molecular ) es la suma de los componentes electrónicos, vibracionales, rotacionales, nucleares y traslacionales, de modo que: donde E _electrónico es un valor propio del hamiltoniano molecular electrónico (el valor de la energía potencial superficial ) en la geometría de equilibrio de la molécula .$${\displaystyle E=E_{\text{electronic}}+E_{\text{vibrational}}+E_{\text{rotational}}+E_{\text{nuclear}}+E_{\text{translational}}}$$

Los niveles de energía molecular se identifican mediante los símbolos de los términos moleculares . Las energías específicas de estos componentes varían según el estado energético específico y la sustancia.

Hay varios tipos de diagramas de niveles de energía para los enlaces entre átomos en una molécula.

Ejemplos

Diagramas de orbitales moleculares , diagramas de Jablonski y diagramas de Franck-Condon .

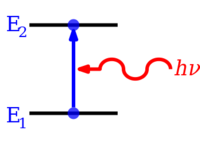
Los electrones en los átomos y moléculas pueden cambiar (hacer transiciones en) los niveles de energía emitiendo o absorbiendo un fotón (de radiación electromagnética ), cuya energía debe ser exactamente igual a la diferencia de energía entre los dos niveles.

Los electrones también pueden eliminarse por completo de una especie química como un átomo, una molécula o un ion . La eliminación completa de un electrón de un átomo puede ser una forma de ionización , que consiste en mover efectivamente el electrón a un orbital con un número cuántico principal infinito , en efecto tan lejos que prácticamente no tiene más efecto sobre el átomo restante (ion). Para varios tipos de átomos, existen energías de ionización 1.ª, 2.ª, 3.ª, etc. para eliminar el 1.º, luego el 2.º, luego el 3.º, etc. de los electrones de mayor energía, respectivamente, del átomo originalmente en el estado fundamental . También se puede liberar energía en cantidades opuestas correspondientes, a veces en forma de energía fotónica , cuando se agregan electrones a iones con carga positiva o, a veces, a átomos. Las moléculas también pueden experimentar transiciones en sus niveles de energía vibracional o rotacional. Las transiciones de nivel de energía también pueden ser no radiativas, lo que significa que no está involucrada la emisión o absorción de un fotón.

Si un átomo, ion o molécula está en el nivel de energía más bajo posible, se dice que él y sus electrones están en el estado fundamental . Si está en un nivel de energía más alto, se dice que está excitado , o cualquier electrón que tenga una energía más alta que el estado fundamental está excitado . Una especie de este tipo puede excitarse a un nivel de energía más alto absorbiendo un fotón cuya energía sea igual a la diferencia de energía entre los niveles. Por el contrario, una especie excitada puede ir a un nivel de energía más bajo emitiendo espontáneamente un fotón igual a la diferencia de energía. La energía de un fotón es igual a la constante de Planck ( h ) multiplicada por su frecuencia ( f ) y, por lo tanto, es proporcional a su frecuencia, o inversamente a su longitud de onda ( λ ). ^[4]

ΔE = hf = hc  /  λ ,​

ya que c , la velocidad de la luz, es igual a fλ ^[4]

En consecuencia, muchos tipos de espectroscopia se basan en la detección de la frecuencia o longitud de onda de los fotones emitidos o absorbidos para proporcionar información sobre el material analizado, incluida información sobre los niveles de energía y la estructura electrónica de los materiales obtenidos mediante el análisis del espectro .

Un asterisco se usa comúnmente para designar un estado excitado. Una transición electrónica en el enlace de una molécula desde un estado fundamental a un estado excitado puede tener una designación como σ → σ*, π → π*, o n → π* que significa excitación de un electrón desde un orbital de enlace σ a uno  antienlazante σ , desde un orbital de enlace π a uno antienlazante π, o desde un orbital no enlazante n a uno antienlazante π. ^{[4] [5]} Las transiciones electrónicas inversas para todos estos tipos de moléculas excitadas también son posibles para regresar a sus estados fundamentales, que pueden designarse como σ* → σ, π* → π, o π* → n.

Una transición en un nivel de energía de un electrón en una molécula puede combinarse con una transición vibracional y llamarse transición vibrónica . Una transición vibracional y rotacional pueden combinarse mediante acoplamiento rovibratorio . En el acoplamiento rovibrónico , las transiciones de electrones se combinan simultáneamente con transiciones vibracionales y rotacionales. Los fotones involucrados en las transiciones pueden tener energía de varios rangos en el espectro electromagnético, como rayos X , ultravioleta , luz visible , infrarrojos o radiación de microondas , dependiendo del tipo de transición. De manera muy general, las diferencias de nivel de energía entre estados electrónicos son mayores, las diferencias entre niveles vibracionales son intermedias y las diferencias entre niveles rotacionales son menores, aunque puede haber superposición. Los niveles de energía traslacional son prácticamente continuos y pueden calcularse como energía cinética utilizando la mecánica clásica .

Una temperatura más alta hace que los átomos y moléculas de fluidos se muevan más rápido, lo que aumenta su energía traslacional y excita térmicamente las moléculas a amplitudes promedio más altas de modos vibracionales y rotacionales (excita las moléculas a niveles de energía interna más altos). Esto significa que a medida que aumenta la temperatura, las contribuciones traslacionales, vibracionales y rotacionales a la capacidad térmica molecular permiten que las moléculas absorban calor y retengan más energía interna . La conducción de calor generalmente ocurre cuando las moléculas o átomos chocan y transfieren el calor entre sí. A temperaturas aún más altas, los electrones pueden excitarse térmicamente a orbitales de mayor energía en átomos o moléculas. Una caída posterior de un electrón a un nivel de energía más bajo puede liberar un fotón, lo que provoca un brillo posiblemente coloreado.

Un electrón más alejado del núcleo tiene mayor energía potencial que un electrón más cercano al núcleo, por lo que queda menos ligado al núcleo, ya que su energía potencial es negativa e inversamente dependiente de su distancia al núcleo. ^[6]

Se ha descubierto que los sólidos cristalinos tienen bandas de energía , en lugar de o además de los niveles de energía. Los electrones pueden tomar cualquier energía dentro de una banda vacía. A primera vista, esto parece ser una excepción al requisito de los niveles de energía. Sin embargo, como se muestra en la teoría de bandas , las bandas de energía en realidad están formadas por muchos niveles de energía discretos que están demasiado cerca entre sí para resolverse. Dentro de una banda, el número de niveles es del orden del número de átomos en el cristal, por lo que, aunque los electrones están realmente restringidos a estas energías, parecen ser capaces de tomar un continuo de valores. Los niveles de energía importantes en un cristal son la parte superior de la banda de valencia , la parte inferior de la banda de conducción , el nivel de Fermi , el nivel de vacío y los niveles de energía de cualquier estado defectuoso en el cristal.

• Teoría de la perturbación (mecánica cuántica)
• Química computacional