Momento magnético

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Aislante Permitividad Polarización Energía potencial Electricidad estática Triboelectricidad
Magnetostática Ley de Ampère Ley de Biot-Savart Ley magnética de Gauss Dipolo magnético Campo magnético Flujo magnético Potencial escalar magnético Potencial vectorial magnético Magnetización Permeabilidad Regla de la mano derecha
Electrodinámica Radiación de frenado Radiación ciclotrónica Corriente de desplazamiento Corriente de Foucault Campo electromagnético Inducción electromagnética Pulso electromagnético Radiación electromagnética Ley de Faraday Ecuaciones de Jefimenko Fórmula de Larmor Ley de Lenz Potencial de Liénard-Wiechert Ecuaciones de Londres Fuerza de Lorentz Ecuaciones de Maxwell Tensor de Maxwell Vector de Poynting Radiación de sincrotrón
Red eléctrica Corriente alterna Capacidad Densidad de corriente Corriente continua Corriente eléctrica Energía eléctrica Electrólisis Fuerza electromotriz Impedancia Inductancia Calentamiento Joule Kirchhoff laws Network analysis Ohm law Parallel circuit Resistance Resonant cavities Series circuit Voltage Watt Waveguides
Magnetic circuit AC motor DC motor Electric machine Electric motor Gyrator–capacitor Induction motor Linear motor Magnetomotive force Permeance Reluctance (complex) Reluctance (real) Rotor Stator Transformer
Covariant formulation Electromagnetic tensor Electromagnetism and special relativity Four-current Four-potential Mathematical descriptions Maxwell equations in curved spacetime Relativistic electromagnetism Stress–energy tensor
Scientists Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Helmholtz Henry Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Poisson Poynting Ritchie Savart Singer Steinmetz Tesla Thomson Volta Weber Wiechert
v t e

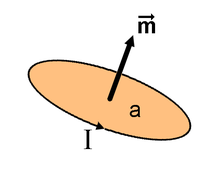Momento magnético m de una corriente I , que encierra un área a .
Símbolos comunes	metro
Unidad SI	Amperio - metro 2
En unidades base del SI	m2⋅A​​​
Dimensión	L2yo​​

En electromagnetismo , el momento magnético o momento dipolar magnético es la combinación de fuerza y ​​orientación de un imán u otro objeto o sistema que ejerce un campo magnético . El momento dipolar magnético de un objeto determina la magnitud del par que experimenta el objeto en un campo magnético determinado. Cuando se aplica el mismo campo magnético, los objetos con momentos magnéticos mayores experimentan pares mayores. La fuerza (y dirección) de este par depende no solo de la magnitud del momento magnético sino también de su orientación relativa a la dirección del campo magnético. Su dirección apunta del polo sur al polo norte del imán (es decir, dentro del imán).

El momento magnético también expresa el efecto de fuerza magnética de un imán. El campo magnético de un dipolo magnético es proporcional a su momento dipolar magnético. El componente dipolar del campo magnético de un objeto es simétrico respecto de la dirección de su momento dipolar magnético y disminuye como el cubo inverso de la distancia al objeto.

Entre los ejemplos de objetos o sistemas que producen momentos magnéticos se incluyen: imanes permanentes; objetos astronómicos como muchos planetas , incluida la Tierra , y algunas lunas , estrellas , etc.; diversas moléculas ; partículas elementales (por ejemplo, electrones ); compuestos de partículas elementales ( protones y neutrones , como el núcleo de un átomo); y bucles de corriente eléctrica como los ejercidos por electroimanes .

El momento magnético se puede definir como un vector (en realidad, un pseudovector ) que relaciona el par de torsión de alineación sobre el objeto de un campo magnético aplicado externamente con el propio vector de campo. La relación viene dada por: ^[1] donde τ es el par de torsión que actúa sobre el dipolo, B es el campo magnético externo y m es el momento magnético.$${\displaystyle {\boldsymbol {\tau }}=\mathbf {m} \times \mathbf {B} }$$

Esta definición se basa en cómo se podría, en principio, medir el momento magnético de una muestra desconocida. Para un bucle de corriente, esta definición lleva a que la magnitud del momento dipolar magnético sea igual al producto de la corriente por el área del bucle. Además, esta definición permite el cálculo del momento magnético esperado para cualquier distribución de corriente macroscópica conocida.

Una definición alternativa es útil para los cálculos termodinámicos del momento magnético. En esta definición, el momento dipolar magnético de un sistema es el gradiente negativo de su energía intrínseca, U _int , con respecto al campo magnético externo:$${\displaystyle \mathbf {m} =-{\hat {\mathbf {x} }}{\frac {\partial U_{\text{int}}}{\partial B_{x}}}-{\hat {\mathbf {y} }}{\frac {\partial U_{\text{int}}}{\partial B_{y}}}-{\hat {\mathbf {z} }}{\frac {\partial U_{\text{int}}}{\partial B_{z}}}.}$$

En términos generales, la energía intrínseca incluye la energía del propio campo del sistema más la energía de los mecanismos internos del sistema. Por ejemplo, para un átomo de hidrógeno en un estado 2p en un campo externo, la energía del propio campo es despreciable, por lo que la energía interna es esencialmente la energía propia del estado 2p, que incluye la energía potencial de Coulomb y la energía cinética del electrón. La energía del campo de interacción entre los dipolos internos y los campos externos no forma parte de esta energía interna. ^[2]

La unidad de momento magnético en las unidades básicas del Sistema Internacional de Unidades (SI) es A⋅m ² , donde A es amperio (unidad básica del SI para la corriente) y m es metro (unidad básica del SI para la distancia). Esta unidad tiene equivalentes en otras unidades derivadas del SI, entre ellas: ^{[3] [4]}

$${\displaystyle \mathrm {A\cdot m^{2}} ={\frac {\mathrm {N\cdot m} }{\mathrm {T} }}={\frac {\mathrm {J} }{\mathrm {T} }},}$$

donde N es newton (unidad de fuerza derivada del SI), T es tesla (unidad de densidad de flujo magnético derivada del SI) y J es joule (unidad de energía derivada del SI ). ^{[5] : 20–21} Aunque el torque (N·m) y la energía (J) son dimensionalmente equivalentes, los torques nunca se expresan en unidades de energía. ^{[5] : 23}

En el sistema CGS existen varios conjuntos diferentes de unidades de electromagnetismo, de los cuales los principales son ESU , Gaussian y EMU . Entre estos, existen dos unidades alternativas (no equivalentes) de momento dipolar magnético:$${\displaystyle 1{\text{ statA}}{\cdot }{\text{cm}}^{2}=3.33564095\times 10^{-14}{\text{ A}}{\cdot }{\text{m}}^{2}~~{\text{ (ESU)}}}$$$${\displaystyle 1\;{\frac {\text{erg}}{\text{G}}}=10^{-3}{\text{ A}}{\cdot }{\text{m}}^{2}~~{\text{ (Gaussian and EMU),}}}$$

donde statA son estatamperios , cm son centímetros , erg son ergios y G son gauss . La relación entre estas dos unidades CGS no equivalentes (EMU/ESU) es igual a la velocidad de la luz en el espacio libre, expresada en cm ⋅ s ⁻¹ .

Todas las fórmulas de este artículo son correctas en unidades del SI ; es posible que sea necesario modificarlas para su uso en otros sistemas de unidades. Por ejemplo, en unidades del SI, un bucle de corriente con corriente I y área A tiene un momento magnético IA (ver más abajo), pero en unidades gaussianas el momento magnético es ⁠Iowa/do⁠ .

Otras unidades para medir el momento dipolar magnético incluyen el magnetón de Bohr y el magnetón nuclear .

Los momentos magnéticos de los objetos se miden normalmente con dispositivos llamados magnetómetros , aunque no todos los magnetómetros miden el momento magnético: algunos están configurados para medir el campo magnético . Sin embargo, si se conoce lo suficientemente bien el campo magnético que rodea a un objeto, entonces se puede calcular el momento magnético a partir de ese campo magnético. ^{[ cita requerida ]}

El momento magnético es una cantidad que describe la fuerza magnética de un objeto entero. A veces, sin embargo, es útil o necesario saber qué parte del momento magnético neto del objeto es producido por una porción particular de ese imán. Por lo tanto, es útil definir el campo de magnetización M como: donde m _{Δ V} y V _{Δ V} son el momento dipolar magnético y el volumen de una porción suficientemente pequeña del imán Δ V . Esta ecuación a menudo se representa utilizando la notación derivada de modo que donde d m es el momento magnético elemental y d V es el elemento de volumen . Por lo tanto, el momento magnético neto del imán m es donde la integral triple denota la integración sobre el volumen del imán . Para la magnetización uniforme (donde tanto la magnitud como la dirección de M son las mismas para todo el imán (como un imán de barra recto) la última ecuación se simplifica a: donde V es el volumen del imán de barra.$${\displaystyle \mathbf {M} ={\frac {\mathbf {m} _{\Delta V}}{V_{\Delta V}}},}$$$${\displaystyle \mathbf {M} ={\frac {\mathrm {d} \mathbf {m} }{\mathrm {d} V}},}$$$${\displaystyle \mathbf {m} =\iiint \mathbf {M} \,\mathrm {d} V,}$$$${\displaystyle \mathbf {m} =\mathbf {M} V,}$$

Sin embargo, la magnetización no suele figurar como parámetro material en los materiales ferromagnéticos disponibles comercialmente . En su lugar, el parámetro que se incluye es la densidad de flujo residual (o remanencia), denominada B _r . La fórmula necesaria en este caso para calcular m en (unidades de A⋅m ² ) es:$${\displaystyle \mathbf {m} ={\frac {1}{\mu _{0}}}\mathbf {B} _{\text{r}}V,}$$

dónde:

• B _r es la densidad de flujo residual, expresada en teslas .
• V es el volumen del imán (en m ³ ).
• μ ₀ es la permeabilidad del vacío (4π × 10 ⁻⁷  H/m ). ^[6]

La explicación clásica preferida de un momento magnético ha cambiado con el tiempo. Antes de la década de 1930, los libros de texto explicaban el momento utilizando cargas magnéticas puntuales hipotéticas. Desde entonces, la mayoría lo han definido en términos de corrientes amperianas. ^[7] En los materiales magnéticos, la causa del momento magnético son los estados de momento angular orbital y de espín de los electrones , y varía dependiendo de si los átomos en una región están alineados con átomos en otra. ^{[ cita requerida ]}

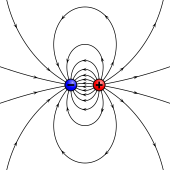
Las fuentes de momentos magnéticos en los materiales pueden representarse mediante polos en analogía con la electrostática . Esto a veces se conoce como el modelo de Gilbert. ^{[8] : 258} En este modelo, un pequeño imán se modela mediante un par de monopolos magnéticos ficticios de igual magnitud pero polaridad opuesta . Cada polo es la fuente de fuerza magnética que se debilita con la distancia. Dado que los polos magnéticos siempre vienen en pares, sus fuerzas se cancelan parcialmente entre sí porque mientras un polo atrae, el otro repele. Esta cancelación es mayor cuando los polos están cerca uno del otro, es decir, cuando el imán de barra es corto. La fuerza magnética producida por un imán de barra, en un punto dado en el espacio, depende por lo tanto de dos factores: la fuerza p de sus polos ( fuerza del polo magnético ), y el vector que los separa. El momento dipolar magnético m está relacionado con los polos ficticios como ^[7]${\displaystyle \mathrm {\boldsymbol {\ell }} }$$${\displaystyle \mathbf {m} =p\,\mathrm {\boldsymbol {\ell }} \,.}$$

Apunta en la dirección del polo sur al polo norte. La analogía con los dipolos eléctricos no debe llevarse demasiado lejos porque los dipolos magnéticos están asociados con el momento angular (ver Relación con el momento angular). Sin embargo, los polos magnéticos son muy útiles para los cálculos magnetostáticos , particularmente en aplicaciones a ferroimanes . ^[7] Los profesionales que utilizan el enfoque del polo magnético generalmente representan el campo magnético por el campo irrotacional H , en analogía con el campo eléctrico E .

Después de que Hans Christian Ørsted descubriera que las corrientes eléctricas producen un campo magnético y André-Marie Ampère descubriera que las corrientes eléctricas se atraen y se repelen entre sí de manera similar a los imanes, era natural plantear la hipótesis de que todos los campos magnéticos se deben a bucles de corriente eléctrica. En este modelo desarrollado por Ampère, el dipolo magnético elemental que compone todos los imanes es un bucle amperiano de corriente I suficientemente pequeño . El momento dipolar de este bucle es donde S es el área del bucle. La dirección del momento magnético es en una dirección normal al área encerrada por la corriente consistente con la dirección de la corriente utilizando la regla de la mano derecha.$${\displaystyle \mathbf {m} =I{\boldsymbol {S}},}$$

El momento dipolar magnético se puede calcular para una distribución de corriente localizada (no se extiende hasta el infinito) suponiendo que conocemos todas las corrientes involucradas. Convencionalmente, la derivación comienza a partir de una expansión multipolar del potencial vectorial . Esto lleva a la definición del momento dipolar magnético como: donde × es el producto vectorial , r es el vector de posición y j es la densidad de corriente eléctrica y la integral es una integral de volumen. ^{[9] : § 5.6} Cuando la densidad de corriente en la integral se reemplaza por un bucle de corriente I en un plano que encierra un área S, entonces la integral de volumen se convierte en una integral de línea y el momento dipolar resultante se convierte en que es como se deriva el momento dipolar magnético para un bucle amperiano.$${\displaystyle \mathbf {m} ={\tfrac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} (\mathbf {r} )\,\mathrm {d} V,}$$$${\displaystyle \mathbf {m} =I\mathbf {S} ,}$$

Los profesionales que utilizan el modelo de bucle de corriente generalmente representan el campo magnético mediante el campo solenoidal B , análogo al campo electrostático D.

Una generalización del bucle de corriente anterior es una bobina o solenoide . Su momento es la suma vectorial de los momentos de las espiras individuales. Si el solenoide tiene N espiras idénticas (bobinado de una sola capa) y área vectorial S ,$${\displaystyle \mathbf {m} =NI\mathbf {S} .}$$

Al calcular los momentos magnéticos de materiales o moléculas a nivel microscópico, a menudo resulta conveniente utilizar un tercer modelo para el momento magnético que aprovecha la relación lineal entre el momento angular y el momento magnético de una partícula. Si bien esta relación es sencilla de desarrollar para corrientes macroscópicas utilizando el modelo de bucle amperiano (véase más adelante), ni el modelo de polo magnético ni el modelo de bucle amperiano representan verdaderamente lo que ocurre a nivel atómico y molecular. En ese nivel se debe utilizar la mecánica cuántica . Afortunadamente, la relación lineal entre el momento dipolar magnético de una partícula y su momento angular sigue siendo válida, aunque es diferente para cada partícula. Además, se debe tener cuidado para distinguir entre el momento angular intrínseco (o espín ) de la partícula y el momento angular orbital de la partícula. Véase más adelante para obtener más detalles.

El par τ sobre un objeto que tiene un momento dipolar magnético m en un campo magnético uniforme B es:$${\displaystyle {\boldsymbol {\tau }}=\mathbf {m} \times \mathbf {B} .}$$

Esto es válido por el momento debido a cualquier distribución de corriente localizada siempre que el campo magnético sea uniforme. Para B no uniforme, la ecuación también es válida para el par en torno al centro del dipolo magnético, siempre que el dipolo magnético sea lo suficientemente pequeño. ^{[8] : 257}

Un electrón, núcleo o átomo colocado en un campo magnético uniforme precesará con una frecuencia conocida como frecuencia de Larmor . Véase Resonancia .

Un momento magnético en un campo magnético producido externamente tiene una energía potencial U :$${\displaystyle U=-\mathbf {m} \cdot \mathbf {B} }$$

En un caso en el que el campo magnético externo no es uniforme, habrá una fuerza, proporcional al gradiente del campo magnético , que actuará sobre el propio momento magnético. Hay dos expresiones para la fuerza que actúa sobre un dipolo magnético, dependiendo de si el modelo utilizado para el dipolo es un bucle de corriente o dos monopolos (análogos al dipolo eléctrico). ^[10] La fuerza obtenida en el caso de un modelo de bucle de corriente es$${\displaystyle \mathbf {F} _{\text{loop}}=\nabla \left(\mathbf {m} \cdot \mathbf {B} \right).}$$

Suponiendo la existencia de un monopolo magnético, la fuerza se modifica de la siguiente manera:$${\displaystyle {\begin{aligned}\mathbf {F} _{\text{loop}}&=\left(\mathbf {m} \times \nabla \right)\times \mathbf {B} \\[1ex]&=\nabla \left(\mathbf {m} \cdot \mathbf {B} \right)-\left(\nabla \cdot \mathbf {B} \right)\mathbf {m} \end{aligned}}}$$

En el caso de utilizar un par de monopolos (es decir, el modelo de dipolo eléctrico), la fuerza es Y uno puede expresarse en términos del otro a través de la relación$${\displaystyle \mathbf {F} _{\text{dipole}}=\left(\mathbf {m} \cdot \nabla \right)\mathbf {B} .}$$$${\displaystyle \mathbf {F} _{\text{loop}}=\mathbf {F} _{\text{dipole}}+\mathbf {m} \times \left(\nabla \times \mathbf {B} \right)-\left(\nabla \cdot \mathbf {B} \right)\mathbf {m} .}$$

En todas estas expresiones, m es el dipolo y B es el campo magnético en su posición. Nótese que si no hay corrientes ni campos eléctricos variables en el tiempo ni carga magnética, ∇× B = 0 , ∇⋅ B = 0 y las dos expresiones concuerdan.

Se puede relacionar el momento magnético de un sistema con la energía libre de ese sistema. ^[11] En un campo magnético uniforme B , la energía libre F se puede relacionar con el momento magnético M del sistema como donde S es la entropía del sistema y T es la temperatura. Por lo tanto, el momento magnético también se puede definir en términos de la energía libre de un sistema como$${\displaystyle \mathrm {d} F=-S\,\mathrm {d} T-\mathbf {M} \,\cdot \mathrm {d} \mathbf {B} }$$$${\displaystyle m=\left.-{\frac {\partial F}{\partial B}}\right|_{T}.}$$

Además, un campo magnético aplicado puede cambiar el momento magnético del propio objeto; por ejemplo, magnetizándolo. Este fenómeno se conoce como magnetismo . Un campo magnético aplicado puede voltear los dipolos magnéticos que componen el material provocando tanto paramagnetismo como ferromagnetismo . Además, el campo magnético puede afectar a las corrientes que crean los campos magnéticos (como las órbitas atómicas), lo que provoca diamagnetismo .

Cualquier sistema que posea un momento dipolar magnético neto m producirá un campo magnético dipolar (descrito a continuación) en el espacio que rodea al sistema. Si bien el campo magnético neto producido por el sistema también puede tener componentes multipolares de orden superior , estos disminuirán con la distancia más rápidamente, de modo que solo el componente dipolar dominará el campo magnético del sistema a distancias lejanas de él.

El campo magnético de un dipolo magnético depende de la fuerza y ​​la dirección del momento magnético de un imán , pero disminuye como el cubo de la distancia, de modo que:${\displaystyle \mathbf {m} }$$${\displaystyle \mathbf {H} (\mathbf {r} )={\frac {1}{4\pi }}\left({\frac {3\mathbf {r} (\mathbf {m} \cdot \mathbf {r} )}{|\mathbf {r} |^{5}}}-{\frac {\mathbf {m} }{|\mathbf {r} |^{3}}}\right),}$$

donde es el campo magnético producido por el imán y es un vector desde el centro del dipolo magnético hasta la ubicación donde se mide el campo magnético. La naturaleza cúbica inversa de esta ecuación se ve más fácilmente expresando el vector de ubicación como el producto de su magnitud por el vector unitario en su dirección ( ) de modo que:${\displaystyle \mathbf {H} }$${\displaystyle \mathbf {r} }$${\displaystyle \mathbf {r} }$${\displaystyle \mathbf {r} =|\mathbf {r} |\mathbf {\hat {r}} }$$${\displaystyle \mathbf {H} (\mathbf {r} )={\frac {1}{4\pi }}{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}.}$$

Las ecuaciones equivalentes para el campo magnético son las mismas excepto por un factor multiplicativo de μ ₀ =${\displaystyle \mathbf {B} }$4 π × 10 ⁻⁷  H / m , donde μ ₀ se conoce como la permeabilidad al vacío . Por ejemplo:$${\displaystyle \mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}.}$$

Como se discutió anteriormente, la fuerza ejercida por un bucle dipolar con momento m ₁ sobre otro con momento m ₂ es donde B ₁ es el campo magnético debido al momento m ₁ . El resultado de calcular el gradiente es ^{[12] [13]} donde r̂ es el vector unitario que apunta del imán 1 al imán 2 y r es la distancia. Una expresión equivalente es ^[13] La fuerza que actúa sobre m ₁ es en la dirección opuesta.$${\displaystyle \mathbf {F} =\nabla \left(\mathbf {m} _{2}\cdot \mathbf {B} _{1}\right),}$$$${\displaystyle \mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\frac {3\mu _{0}}{4\pi |\mathbf {r} |^{4}}}\left[\mathbf {m} _{2}(\mathbf {m} _{1}\cdot {\hat {\mathbf {r} }})+\mathbf {m} _{1}(\mathbf {m} _{2}\cdot {\hat {\mathbf {r} }})+{\hat {\mathbf {r} }}(\mathbf {m} _{1}\cdot \mathbf {m} _{2})-5{\hat {\mathbf {r} }}(\mathbf {m} _{1}\cdot {\hat {\mathbf {r} }})(\mathbf {m} _{2}\cdot {\hat {\mathbf {r} }})\right],}$$$${\displaystyle \mathbf {F} ={\frac {3\mu _{0}}{4\pi |\mathbf {r} |^{4}}}\left[({\hat {\mathbf {r} }}\times \mathbf {m} _{1})\times \mathbf {m} _{2}+({\hat {\mathbf {r} }}\times \mathbf {m} _{2})\times \mathbf {m} _{1}-2{\hat {\mathbf {r} }}(\mathbf {m} _{1}\cdot \mathbf {m} _{2})+5{\hat {\mathbf {r} }}({\hat {\mathbf {r} }}\times \mathbf {m} _{1})\cdot ({\hat {\mathbf {r} }}\times \mathbf {m} _{2})\right].}$$

El par del imán 1 sobre el imán 2 es$${\displaystyle {\boldsymbol {\tau }}=\mathbf {m} _{2}\times \mathbf {B} _{1}.}$$

El campo magnético de cualquier imán puede ser modelado por una serie de términos, cada uno de los cuales es más complicado (tiene un detalle angular más fino) que el anterior. Los primeros tres términos de esa serie se denominan monopolo ( representado por un polo norte o sur magnético aislado), dipolo (representado por dos polos magnéticos iguales y opuestos) y cuadrupolo (representado por cuatro polos que juntos forman dos dipolos iguales y opuestos). La magnitud del campo magnético para cada término disminuye progresivamente más rápido con la distancia que el término anterior, de modo que a distancias suficientemente grandes dominará el primer término distinto de cero. ^{[ cita requerida ]}

En muchos imanes, el primer término distinto de cero es el momento dipolar magnético (hasta la fecha, no se han detectado experimentalmente monopolos magnéticos aislados). Un dipolo magnético es el límite de un bucle de corriente o de un par de polos cuando las dimensiones de la fuente se reducen a cero mientras se mantiene constante el momento. Mientras estos límites solo se apliquen a campos alejados de las fuentes, son equivalentes. Sin embargo, los dos modelos dan predicciones diferentes para el campo interno (ver a continuación).

Tradicionalmente, las ecuaciones para el momento dipolar magnético (y términos de orden superior) se derivan de cantidades teóricas llamadas potenciales magnéticos ^{[9] : § 5.6} que son más simples de manejar matemáticamente que los campos magnéticos. ^{[ cita requerida ]}

En el modelo de polos magnéticos, el campo magnético relevante es el campo desmagnetizante . Como la parte desmagnetizante de no incluye, por definición, la parte de debida a corrientes libres, existe un potencial escalar magnético tal que${\displaystyle \mathbf {H} }$${\displaystyle \mathbf {H} }$${\displaystyle \mathbf {H} }$$${\displaystyle {\mathbf {H} }({\mathbf {r} })=-\nabla \psi .}$$

En el modelo de bucle amperiano, el campo magnético relevante es la inducción magnética . Como no existen monopolos magnéticos, existe un potencial vectorial magnético tal que${\displaystyle \mathbf {B} }$$${\displaystyle \mathbf {B} (\mathbf {r} )=\nabla \times \mathbf {A} .}$$

Ambos potenciales se pueden calcular para cualquier distribución de corriente arbitraria (para el modelo de bucle amperiano) o distribución de carga magnética (para el modelo de carga magnética) siempre que se limiten a una región lo suficientemente pequeña para dar: donde es la densidad de corriente en el modelo de bucle amperiano, es la densidad de fuerza del polo magnético en analogía con la densidad de carga eléctrica que conduce al potencial eléctrico, y las integrales son las integrales de volumen (triples) sobre las coordenadas que forman . Los denominadores de estas ecuaciones se pueden expandir utilizando la expansión multipolar para dar una serie de términos que tienen mayor potencia de distancias en el denominador. Por lo tanto, el primer término distinto de cero dominará para distancias grandes. El primer término distinto de cero para el potencial vectorial es: donde es: donde × es el producto vectorial , r es el vector de posición y j es la densidad de corriente eléctrica y la integral es una integral de volumen.$${\displaystyle {\begin{aligned}\mathbf {A} \left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int {\frac {\mathbf {j} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} V',\\[1ex]\psi \left(\mathbf {r} ,t\right)&={\frac {1}{4\pi }}\int {\frac {\rho \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} V',\end{aligned}}}$$${\displaystyle \mathbf {j} }$${\displaystyle \rho }$${\displaystyle \mathbf {r} '}$$${\displaystyle \mathbf {A} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}{\frac {\mathbf {m} \times \mathbf {r} }{|\mathbf {r} |^{3}}},}$$${\displaystyle \mathbf {m} }$$${\displaystyle \mathbf {m} ={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,\mathrm {d} V,}$$

En la perspectiva del polo magnético, el primer término distinto de cero del potencial escalar es$${\displaystyle \psi (\mathbf {r} )={\frac {\mathbf {m} \cdot \mathbf {r} }{4\pi |\mathbf {r} |^{3}}}.}$$

Aquí se puede representar en términos de densidad de fuerza del polo magnético, pero se expresa de manera más útil en términos del campo de magnetización como:${\displaystyle \mathbf {m} }$$${\displaystyle \mathbf {m} =\iiint \mathbf {M} \,\mathrm {d} V.}$$

Se utiliza el mismo símbolo para ambas ecuaciones, ya que producen resultados equivalentes fuera del imán.${\displaystyle \mathbf {m} }$

Por lo tanto, la densidad de flujo magnético para un dipolo magnético en el modelo de bucle amperiano es$${\displaystyle \mathbf {B} (\mathbf {r} )=\nabla \times {\mathbf {A} }={\frac {\mu _{0}}{4\pi }}\left({\frac {3\mathbf {r} (\mathbf {m} \cdot \mathbf {r} )}{|\mathbf {r} |^{5}}}-{\frac {\mathbf {m} }{|\mathbf {r} |^{3}}}\right).}$$

Además, la intensidad del campo magnético es${\displaystyle \mathbf {H} }$$${\displaystyle {\mathbf {H} }({\mathbf {r} })=-\nabla \psi ={\frac {1}{4\pi }}\left({\frac {3\mathbf {r} (\mathbf {m} \cdot \mathbf {r} )}{|\mathbf {r} |^{5}}}-{\frac {\mathbf {m} }{|\mathbf {r} |^{3}}}\right).}$$

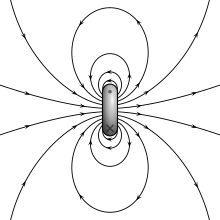
Los dos modelos de dipolo (polos magnéticos o bucle de corriente) dan las mismas predicciones para el campo magnético lejos de la fuente. Sin embargo, dentro de la región de la fuente, dan predicciones diferentes. El campo magnético entre polos (ver la figura del modelo de polo magnético) está en la dirección opuesta al momento magnético (que apunta de la carga negativa a la carga positiva), mientras que dentro de un bucle de corriente está en la misma dirección (ver la figura a la derecha). Los límites de estos campos también deben ser diferentes a medida que las fuentes se reducen a tamaño cero. Esta distinción solo importa si se utiliza el límite dipolar para calcular campos dentro de un material magnético. ^[7]

Si se forma un dipolo magnético tomando un "polo norte" y un "polo sur", acercándolos cada vez más pero manteniendo constante el producto de la carga del polo magnético y la distancia, el campo límite es ^[7]$${\displaystyle \mathbf {H} (\mathbf {r} )={\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}-{\frac {4\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right].}$$

Si se forma un dipolo magnético haciendo un bucle de corriente cada vez más pequeño, pero manteniendo constante el producto de la corriente por el área, el campo límite es A diferencia de las expresiones de la sección anterior, este límite es correcto para el campo interno del dipolo. ^{[7] [9] : 184}$${\displaystyle \mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}+{\frac {8\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right].}$$

Estos campos están relacionados por B = μ ₀ ( H + M ) , donde M ( r ) = m δ ( r ) es la magnetización .

El momento magnético tiene una estrecha relación con el momento angular , denominado efecto giromagnético . Este efecto se expresa a escala macroscópica en el efecto Einstein-de Haas o «rotación por magnetización», y su inverso, el efecto Barnett o «magnetización por rotación». ^[1] Además, un par aplicado a un dipolo magnético relativamente aislado, como un núcleo atómico, puede provocar su precesión (rotación sobre el eje del campo aplicado). Este fenómeno se utiliza en la resonancia magnética nuclear . ^{[ cita requerida ]}

Al considerar un dipolo magnético como un bucle de corriente, se pone de manifiesto la estrecha relación entre el momento magnético y el momento angular. Dado que las partículas que crean la corriente (al girar alrededor del bucle) tienen carga y masa, tanto el momento magnético como el momento angular aumentan con la velocidad de rotación. La relación entre ambos se denomina relación giromagnética o, de modo que: ^{[14] [15]} donde es el momento angular de la partícula o partículas que están creando el momento magnético.${\displaystyle \gamma }$$${\displaystyle \mathbf {m} =\gamma \,\mathbf {L} ,}$$${\displaystyle \mathbf {L} }$

En el modelo de bucle amperiano, que se aplica a corrientes macroscópicas, la relación giromagnética es la mitad de la relación carga-masa . Esto se puede mostrar de la siguiente manera. El momento angular de una partícula cargada en movimiento se define como: donde μ es la masa de la partícula y v es la velocidad de la partícula . Por lo tanto, el momento angular de la gran cantidad de partículas cargadas que forman una corriente es: donde ρ es la densidad de masa de las partículas en movimiento. Por convención, la dirección del producto vectorial se da mediante la regla de la mano derecha . ^[16]$${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} =\mu \,\mathbf {r} \times \mathbf {v} ,}$$$${\displaystyle \mathbf {L} =\iiint _{V}\,\mathbf {r} \times (\rho \mathbf {v} )\,\mathrm {d} V\,,}$$

Esto es similar al momento magnético creado por la gran cantidad de partículas cargadas que componen esa corriente: donde y es la densidad de carga de las partículas cargadas en movimiento.$${\displaystyle \mathbf {m} ={\tfrac {1}{2}}\iiint _{V}\mathbf {r} \times (\rho _{Q}\mathbf {v} )\,\mathrm {d} V\,,}$$${\displaystyle \mathbf {j} =\rho _{Q}\mathbf {v} }$${\displaystyle \rho _{Q}}$

Comparando las dos ecuaciones se obtiene: donde es la carga de la partícula y es la masa de la partícula.$${\displaystyle \mathbf {m} ={\frac {e}{2\mu }}\,\mathbf {L} \,,}$$${\displaystyle e}$${\displaystyle \mu }$

Aunque las partículas atómicas no pueden describirse con precisión como distribuciones de carga en órbita (y girando) con una relación uniforme entre carga y masa, esta tendencia general se puede observar en el mundo atómico de modo que: donde el factor g depende de la partícula y la configuración. Por ejemplo, el factor g para el momento magnético debido a un electrón que orbita un núcleo es uno, mientras que el factor g para el momento magnético del electrón debido a su momento angular intrínseco ( espín ) es un poco mayor que 2. El factor g de los átomos y las moléculas debe tener en cuenta los momentos orbitales e intrínsecos de sus electrones y, posiblemente, también el momento intrínseco de sus núcleos.$${\displaystyle \mathbf {m} =g\,{\frac {e}{2\mu }}\,\mathbf {L} ,}$$

En el mundo atómico, el momento angular ( spin ) de una partícula es un múltiplo entero (o semientero en el caso de los fermiones) de la constante de Planck reducida ħ . Esta es la base para definir las unidades de momento magnético del magnetón de Bohr (suponiendo la relación carga-masa del electrón ) y el magnetón nuclear (suponiendo la relación carga-masa del protón ). Consulte momento magnético del electrón y magnetón de Bohr para obtener más detalles.

Básicamente, las contribuciones al momento magnético de cualquier sistema pueden provenir de fuentes de dos tipos: 1) el movimiento de cargas eléctricas , como las corrientes eléctricas ; y 2) el magnetismo intrínseco debido al espín de las partículas elementales , como el electrón . ^{[ cita requerida ]}

Las contribuciones debidas a las fuentes del primer tipo se pueden calcular a partir de conocer la distribución de todas las corrientes eléctricas (o, alternativamente, de todas las cargas eléctricas y sus velocidades) dentro del sistema, utilizando las fórmulas siguientes.

Las contribuciones debidas al espín de las partículas suman la magnitud del momento magnético intrínseco de cada partícula elemental, un número fijo, que a menudo se mide experimentalmente con gran precisión. Por ejemplo, el momento magnético de cualquier electrón se mide como−9,284 764 × 10 ⁻²⁴  J/T . ^[17] La ​​dirección del momento magnético de cualquier partícula elemental está determinada enteramente por la dirección de su espín , donde el valor negativo indica que el momento magnético de cualquier electrón es antiparalelo a su espín.

El momento magnético neto de cualquier sistema es una suma vectorial de las contribuciones de uno o ambos tipos de fuentes. Por ejemplo, el momento magnético de un átomo de hidrógeno-1 (el isótopo más ligero del hidrógeno, formado por un protón y un electrón) es una suma vectorial de las siguientes contribuciones:

1. el momento intrínseco del electrón,
2. el movimiento orbital del electrón alrededor del protón,
3. el momento intrínseco del protón.

De manera similar, el momento magnético de un imán de barra es la suma de los momentos magnéticos contribuyentes, que incluyen los momentos magnéticos intrínsecos y orbitales de los electrones desapareados del material del imán y los momentos magnéticos nucleares.

En el caso de un átomo, se suman los espines individuales de los electrones para obtener un espín total, y se suman los momentos angulares orbitales individuales para obtener un momento angular orbital total. Estos dos se suman luego utilizando el acoplamiento del momento angular para obtener un momento angular total. Para un átomo sin momento magnético nuclear, la magnitud del momento dipolar atómico, , es entonces ^[18] donde j es el número cuántico del momento angular total , g _J es el factor g de Landé y μ _B es el magnetón de Bohr . El componente de este momento magnético a lo largo de la dirección del campo magnético es entonces ^[19]${\displaystyle {\mathfrak {m}}_{\text{atom}}}$$${\displaystyle {\mathfrak {m}}_{\text{atom}}=g_{\text{J}}\,\mu _{\text{B}}\,{\sqrt {j\,(j+1)\,}}}$$$${\displaystyle {\mathfrak {m}}_{{\text{atom}},z}=-m\,g_{\text{J}}\,\mu _{\text{B}}\,.}$$

El signo negativo se produce porque los electrones tienen carga negativa.

El número entero m (que no debe confundirse con el momento, ) se denomina número cuántico magnético o número cuántico ecuatorial , que puede tomar cualquiera de los 2 valores j + 1 : ^[20]${\displaystyle {\mathfrak {m}}}$$${\displaystyle -j,\ -(j-1),\ \cdots ,\ -1,\ 0,\ +1,\ \cdots ,\ +(j-1),\ +j~.}$$

Debido al momento angular, la dinámica de un dipolo magnético en un campo magnético difiere de la de un dipolo eléctrico en un campo eléctrico. El campo ejerce un par sobre el dipolo magnético que tiende a alinearlo con el campo. Sin embargo, el par es proporcional a la tasa de cambio del momento angular, por lo que se produce precesión : la dirección del espín cambia. Este comportamiento se describe mediante la ecuación de Landau-Lifshitz-Gilbert : ^{[21] [22]} donde γ es la relación giromagnética , m es el momento magnético, λ es el coeficiente de amortiguamiento y H _eff es el campo magnético efectivo (el campo externo más cualquier campo autoinducido). El primer término describe la precesión del momento sobre el campo efectivo, mientras que el segundo es un término de amortiguamiento relacionado con la disipación de energía causada por la interacción con el entorno.$${\displaystyle {\frac {1}{\gamma }}{\frac {\mathrm {d} \mathbf {m} }{\mathrm {d} t}}=\mathbf {m} \times \mathbf {H} _{\text{eff}}-{\frac {\lambda }{\gamma m}}\mathbf {m} \times {\frac {\mathrm {d} \mathbf {m} }{\mathrm {d} t}}}$$

Los electrones y muchas partículas elementales también tienen momentos magnéticos intrínsecos, cuya explicación requiere un tratamiento mecánico cuántico y se relaciona con el momento angular intrínseco de las partículas, como se analiza en el artículo Momento magnético del electrón . Son estos momentos magnéticos intrínsecos los que dan lugar a los efectos macroscópicos del magnetismo y otros fenómenos, como la resonancia paramagnética electrónica . ^{[ cita requerida ]}

El momento magnético del electrón es donde μ _B es el magnetón de Bohr , S es el espín del electrón y el factor g g _S es 2 según la teoría de Dirac , pero debido a los efectos electrodinámicos cuánticos es ligeramente mayor en la realidad:$${\displaystyle \mathbf {m} _{\text{S}}=-{\frac {g_{\text{S}}\mu _{\text{B}}\mathbf {S} }{\hbar }},}$$ 2.002 319 304 36 . La desviación de 2 se conoce como momento dipolar magnético anómalo .

De nuevo es importante notar que m es una constante negativa multiplicada por el espín , por lo que el momento magnético del electrón es antiparalelo al espín. Esto puede entenderse con la siguiente imagen clásica: si imaginamos que el momento angular del espín es creado por la masa del electrón girando alrededor de algún eje, la corriente eléctrica que esta rotación crea circula en la dirección opuesta, debido a la carga negativa del electrón; tales bucles de corriente producen un momento magnético que es antiparalelo al espín. Por lo tanto, para un positrón (la antipartícula del electrón) el momento magnético es paralelo a su espín.

El sistema nuclear es un sistema físico complejo formado por nucleones, es decir, protones y neutrones . Las propiedades mecánicas cuánticas de los nucleones incluyen, entre otras, el espín. Dado que los momentos electromagnéticos del núcleo dependen del espín de cada nucleón, se pueden observar estas propiedades con mediciones de los momentos nucleares y, más concretamente, del momento dipolar magnético nuclear.

La mayoría de los núcleos más comunes existen en su estado fundamental , aunque los núcleos de algunos isótopos tienen estados excitados de larga duración . Cada estado de energía de un núcleo de un isótopo dado se caracteriza por un momento dipolar magnético bien definido, cuya magnitud es un número fijo, a menudo medido experimentalmente con gran precisión. Este número es muy sensible a las contribuciones individuales de los nucleones, y una medición o predicción de su valor puede revelar información importante sobre el contenido de la función de onda nuclear. Existen varios modelos teóricos que predicen el valor del momento dipolar magnético y una serie de técnicas experimentales que apuntan a realizar mediciones en núcleos a lo largo del diagrama nuclear.

Toda molécula tiene una magnitud de momento magnético bien definida, que puede depender del estado energético de la molécula . Normalmente, el momento magnético total de una molécula es una combinación de las siguientes contribuciones, en orden de su fuerza típica:

• momentos magnéticos debidos a sus espines electrónicos desapareados ( contribución paramagnética ), si la hay
• movimiento orbital de sus electrones, que en el estado fundamental suele ser proporcional al campo magnético externo ( contribución diamagnética )
• el momento magnético combinado de sus espines nucleares , que depende de la configuración del espín nuclear .

• La molécula de dioxígeno , O ₂ , exhibe un fuerte paramagnetismo , debido a los espines desapareados de sus dos electrones más externos.
• La molécula de dióxido de carbono , _CO2 , presenta en su mayoría diamagnetismo , un momento magnético mucho más débil de los orbitales de los electrones que es proporcional al campo magnético externo. El magnetismo nuclear de un isótopo magnético como ^{el 13} C o ^{el 17} O contribuirá al momento magnético de la molécula.
• La molécula de dihidrógeno , H ₂ , en un campo magnético débil (o cero) exhibe magnetismo nuclear y puede estar en una configuración de espín para- u orto- nuclear.
• Muchos complejos de metales de transición son magnéticos. La fórmula basada únicamente en el espín es una buena primera aproximación para los complejos de alto espín de los metales de transición de primera fila . ^[23]

En física atómica y nuclear, el símbolo griego μ representa la magnitud del momento magnético, a menudo medido en magnetones de Bohr o magnetones nucleares , asociado con el giro intrínseco de la partícula y/o con el movimiento orbital de la partícula en un sistema. Los valores de los momentos magnéticos intrínsecos de algunas partículas se dan en la siguiente tabla:

• Órdenes de magnitud (momento magnético)
• Momento (física)
• Momento dipolar eléctrico
• Momento dipolar toroidal
• Susceptibilidad magnética
• Magnetización orbital
• Interacción magnética dipolo-dipolo

• Bowtell, Richard (2009). "μ – Momento magnético". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .