Ley de Gauss

En física (específicamente en electromagnetismo ), la ley de Gauss , también conocida como teorema de flujo de Gauss (o en ocasiones teorema de Gauss), es una de las ecuaciones de Maxwell . Es una aplicación del teorema de divergencia y relaciona la distribución de carga eléctrica con el campo eléctrico resultante .
Definición
En su forma integral , establece que el flujo del campo eléctrico que sale de una superficie cerrada arbitraria es proporcional a la carga eléctrica encerrada por la superficie, independientemente de cómo se distribuya esa carga. Aunque la ley por sí sola no es suficiente para determinar el campo eléctrico a través de una superficie que encierra cualquier distribución de carga, esto puede ser posible en casos en los que la simetría exige uniformidad del campo. Cuando no existe tal simetría, la ley de Gauss se puede utilizar en su forma diferencial , que establece que la divergencia del campo eléctrico es proporcional a la densidad local de carga.
La ley fue formulada por primera vez [1] por Joseph-Louis Lagrange en 1773, [2] seguida por Carl Friedrich Gauss en 1835, [3] ambas en el contexto de la atracción de elipsoides. Es una de las ecuaciones de Maxwell , que forma la base de la electrodinámica clásica . [nota 1] La ley de Gauss se puede utilizar para derivar la ley de Coulomb , [4] y viceversa.
| Artículos sobre |
| Electromagnetismo |
|---|
 |
Descripción cualitativa
En palabras, la ley de Gauss establece:
- El flujo eléctrico neto a través de cualquier superficie cerrada hipotética es igual a 1/ ε 0 veces la carga eléctrica neta contenida dentro de esa superficie cerrada. La superficie cerrada también se conoce como superficie gaussiana. [5]
La ley de Gauss tiene una estrecha similitud matemática con varias leyes de otras áreas de la física, como la ley de Gauss para el magnetismo y la ley de Gauss para la gravedad . De hecho, cualquier ley del inverso del cuadrado se puede formular de manera similar a la ley de Gauss: por ejemplo, la propia ley de Gauss es esencialmente equivalente a la ley de Coulomb , y la ley de Gauss para la gravedad es esencialmente equivalente a la ley de la gravedad de Newton , ambas leyes del inverso del cuadrado.
La ley puede expresarse matemáticamente mediante cálculo vectorial en forma integral y forma diferencial ; ambas son equivalentes ya que están relacionadas por el teorema de divergencia , también llamado teorema de Gauss. Cada una de estas formas a su vez también puede expresarse de dos maneras: en términos de una relación entre el campo eléctrico E y la carga eléctrica total, o en términos del campo de desplazamiento eléctrico D y la carga eléctrica libre . [6]
Ecuación que involucra lamicampo
La ley de Gauss se puede enunciar utilizando el campo eléctrico E o el campo de desplazamiento eléctrico D. En esta sección se muestran algunas de las formas con E ; la forma con D se encuentra a continuación, al igual que otras formas con E.
Forma integral


La ley de Gauss puede expresarse como: [6]
donde Φ E es el flujo eléctrico a través de una superficie cerrada S que encierra un volumen cualquiera V , Q es la carga total encerrada dentro de V , y ε 0 es la constante eléctrica . El flujo eléctrico Φ E se define como una integral de superficie del campo eléctrico:
donde E es el campo eléctrico, d A es un vector que representa un elemento infinitesimal del área de la superficie, [nota 2] y · representa el producto escalar de dos vectores.
En un espacio-tiempo curvo, el flujo de un campo electromagnético a través de una superficie cerrada se expresa como
donde es la velocidad de la luz ; denota los componentes temporales del tensor electromagnético ; es el determinante del tensor métrico ; es un elemento ortonormal de la superficie bidimensional que rodea la carga ; los índices y no coinciden entre sí. [8]
Dado que el flujo se define como una integral del campo eléctrico, esta expresión de la ley de Gauss se denomina forma integral .
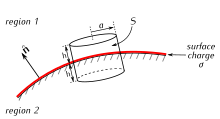
En problemas que involucran conductores fijados a potenciales conocidos, el potencial lejos de ellos se obtiene resolviendo la ecuación de Laplace , ya sea analítica o numéricamente. El campo eléctrico se calcula entonces como el gradiente negativo del potencial. La ley de Gauss permite encontrar la distribución de carga eléctrica: La carga en cualquier región dada del conductor se puede deducir integrando el campo eléctrico para encontrar el flujo a través de una pequeña caja cuyos lados son perpendiculares a la superficie del conductor y notando que el campo eléctrico es perpendicular a la superficie y cero dentro del conductor.
El problema inverso, cuando se conoce la distribución de carga eléctrica y se debe calcular el campo eléctrico, es mucho más difícil. El flujo total a través de una superficie dada brinda poca información sobre el campo eléctrico y puede entrar y salir de la superficie siguiendo patrones arbitrariamente complicados.
Una excepción es si existe alguna simetría en el problema, lo que exige que el campo eléctrico pase a través de la superficie de manera uniforme. Entonces, si se conoce el flujo total, se puede deducir el campo en sí en cada punto. Algunos ejemplos comunes de simetrías que se prestan a la ley de Gauss incluyen: simetría cilíndrica, simetría plana y simetría esférica. Consulte el artículo Superficie gaussiana para ver ejemplos en los que se aprovechan estas simetrías para calcular campos eléctricos.
Forma diferencial
Por el teorema de divergencia , la ley de Gauss puede escribirse alternativamente en forma diferencial :
donde ∇ · E es la divergencia del campo eléctrico, ε 0 es la permitividad del vacío y ρ es la densidad de carga volumétrica total (carga por unidad de volumen).
Equivalencia de formas integrales y diferenciales
Las formas integral y diferencial son matemáticamente equivalentes, según el teorema de divergencia. A continuación se presenta el argumento de forma más específica.
La forma integral de la ley de Gauss es:
Para cualquier superficie cerrada S que contenga carga Q. Por el teorema de divergencia, esta ecuación es equivalente a:
para cualquier volumen V que contenga carga Q . Por la relación entre carga y densidad de carga, esta ecuación es equivalente a: para cualquier volumen V . Para que esta ecuación sea simultáneamente verdadera para cada posible volumen V , es necesario (y suficiente) que los integrandos sean iguales en todas partes. Por lo tanto, esta ecuación es equivalente a:
Por lo tanto, las formas integral y diferencial son equivalentes.
Ecuación que involucra laDcampo
Gratuito, vinculante y de carga total
La carga eléctrica que surge en las situaciones más sencillas de los libros de texto se clasificaría como "carga libre" (por ejemplo, la carga que se transfiere en la electricidad estática o la carga en la placa de un condensador ). Por el contrario, la "carga ligada" surge solo en el contexto de materiales dieléctricos (polarizables). (Todos los materiales son polarizables hasta cierto punto). Cuando estos materiales se colocan en un campo eléctrico externo, los electrones permanecen ligados a sus respectivos átomos, pero se desplazan una distancia microscópica en respuesta al campo, de modo que están más en un lado del átomo que en el otro. Todos estos desplazamientos microscópicos se suman para dar una distribución de carga neta macroscópica, y esto constituye la "carga ligada".
Aunque, desde el punto de vista microscópico, todas las cargas son básicamente iguales, a menudo hay razones prácticas para querer tratar la carga ligada de forma diferente a la carga libre. El resultado es que la ley de Gauss más fundamental, en términos de E (arriba), a veces se expresa en la forma equivalente que se muestra a continuación, que se expresa únicamente en términos de D y de la carga libre.
Forma integral
Esta formulación de la ley de Gauss establece la forma de carga total:
donde Φ D es el flujo del campo D a través de una superficie S que encierra un volumen V , y Q libre es la carga libre contenida en V . El flujo Φ D se define de forma análoga al flujo Φ E del campo eléctrico E a través de S :
Forma diferencial
La forma diferencial de la ley de Gauss, que involucra únicamente carga libre, establece:
donde ∇ · D es la divergencia del campo de desplazamiento eléctrico y ρ libre es la densidad de carga eléctrica libre.
Equivalencia de estados de cuenta totales y de cargos libres
En esta prueba, demostraremos que la ecuación es equivalente a la ecuación Nótese que solo estamos tratando con las formas diferenciales, no con las formas integrales, pero eso es suficiente ya que las formas diferencial e integral son equivalentes en cada caso, por el teorema de divergencia.
Introducimos la densidad de polarización P , que tiene la siguiente relación con E y D : y la siguiente relación con la carga ligada: Ahora, considere las tres ecuaciones: La idea clave es que la suma de las dos primeras ecuaciones es la tercera ecuación. Esto completa la prueba: La primera ecuación es verdadera por definición y, por lo tanto, la segunda ecuación es verdadera si y solo si la tercera ecuación es verdadera. Entonces, la segunda y la tercera ecuaciones son equivalentes, que es lo que queríamos probar.
Ecuación para materiales lineales
En materiales homogéneos , isótropos , no dispersivos y lineales, existe una relación simple entre E y D :
donde ε es la permitividad del material. Para el caso del vacío (también conocido como espacio libre ), ε = ε 0 . En estas circunstancias, la ley de Gauss se modifica a
para la forma integral, y
para la forma diferencial.
Relación con la ley de Coulomb
This article duplicates the scope of other articles, specifically Coulomb's_law#Relation_to_Gauss's_law. |
Derivación de la ley de Gauss a partir de la ley de Coulomb
[ cita requerida ]
En sentido estricto, la ley de Gauss no puede deducirse únicamente de la ley de Coulomb, ya que la ley de Coulomb proporciona únicamente el campo eléctrico debido a una carga puntual electrostática individual . Sin embargo, la ley de Gauss puede demostrarse a partir de la ley de Coulomb si se supone, además, que el campo eléctrico obedece al principio de superposición . El principio de superposición establece que el campo resultante es la suma vectorial de los campos generados por cada partícula (o la integral, si las cargas se distribuyen uniformemente en el espacio).
La ley de Coulomb establece que el campo eléctrico debido a una carga puntual estacionaria es: donde
- e r es el vector unitario radial ,
- r es el radio, | r | ,
- ε 0 es la constante eléctrica ,
- q es la carga de la partícula, que se supone que está ubicada en el origen .
Usando la expresión de la ley de Coulomb, obtenemos el campo total en r usando una integral para sumar el campo en r debido a la carga infinitesimal en cada uno de los otros puntos s en el espacio, para dar donde ρ es la densidad de carga. Si tomamos la divergencia de ambos lados de esta ecuación con respecto a r y usamos el teorema conocido [9]
donde δ ( r ) es la función delta de Dirac , el resultado es
Utilizando la " propiedad de cribado " de la función delta de Dirac, llegamos a que es la forma diferencial de la ley de Gauss, como se deseaba.
Dado que la ley de Coulomb solo se aplica a cargas estacionarias, no hay razón para esperar que la ley de Gauss se cumpla para cargas en movimiento basándose únicamente en esta derivación. De hecho, la ley de Gauss se cumple para cargas en movimiento y, en este sentido, la ley de Gauss es más general que la ley de Coulomb.
Sea un conjunto abierto acotado, y sea el campo eléctrico, con función continua (densidad de carga).
Es cierto todo eso .
Consideremos ahora un conjunto compacto que tiene un límite liso por partes tal que . De ello se deduce que y por lo tanto, para el teorema de divergencia:
Pero porque ,
para el argumento anterior ( y luego )
Por lo tanto, el flujo a través de una superficie cerrada generado por cierta densidad de carga exterior (la superficie) es nulo.
Consideremos ahora , y como la esfera centrada en que tiene como radio (existe porque es un conjunto abierto).
Sean y el campo eléctrico creado dentro y fuera de la esfera respectivamente. Entonces,
- , y
La última igualdad se deduce de la observación de que y del argumento anterior.
El RHS es el flujo eléctrico generado por una esfera cargada, y por lo tanto:
con
Donde la última igualdad se deduce del teorema del valor medio para integrales. Utilizando el teorema de compresión y la continuidad de , se llega a:
Derivación de la ley de Coulomb a partir de la ley de Gauss
En sentido estricto, la ley de Coulomb no puede deducirse únicamente de la ley de Gauss, ya que la ley de Gauss no proporciona ninguna información sobre el rotacional de E (véase la descomposición de Helmholtz y la ley de Faraday ). Sin embargo, la ley de Coulomb puede demostrarse a partir de la ley de Gauss si se supone, además, que el campo eléctrico de una carga puntual es esféricamente simétrico (esta suposición, al igual que la propia ley de Coulomb, es exactamente cierta si la carga está estacionaria y aproximadamente cierta si la carga está en movimiento).
Tomando S en la forma integral de la ley de Gauss como una superficie esférica de radio r , centrada en la carga puntual Q , tenemos
Suponiendo que existe simetría esférica, el integrando es una constante que se puede sacar de la integral. El resultado es donde r̂ es un vector unitario que apunta radialmente en dirección opuesta a la carga. Nuevamente, por simetría esférica, E apunta en la dirección radial, por lo que obtenemos que es esencialmente equivalente a la ley de Coulomb. Por lo tanto, la dependencia de la ley del cuadrado inverso del campo eléctrico en la ley de Coulomb se deduce de la ley de Gauss.
Véase también
- Método de carga de imágenes
- Teorema de unicidad de la ecuación de Poisson
- Lista de ejemplos de la ley de Stigler
Notas
- ^ Las otras tres ecuaciones de Maxwell son: la ley de Gauss para el magnetismo , la ley de inducción de Faraday y la ley de Ampère con la corrección de Maxwell.
- ^ Más específicamente, se piensa que el área infinitesimal es plana y con área d N . El vector d R es normal a este elemento de área y tiene magnitud d A . [7]
Citas
- ^ Duhem, Pierre (1891). "4". Leçons sur l'électricité et le magnétisme [ Lecciones sobre electricidad y magnetismo ] (en francés). vol. 1. París Gauthier-Villars. págs. 22-23. OCLC 1048238688. OL 23310906M .Demuestra que Lagrange tiene prioridad sobre Gauss. Otros, después de Gauss, descubrieron también la "Ley de Gauss".
- ^ Lagrange, Joseph-Louis (1869) [1776]. Serret, Joseph-Alfred ; Darboux, Jean-Gaston (eds.). "Sur l'attraction des sphéroïdes elliptiques" [Sobre la atracción de los esferoides elípticos]. Œuvres de Lagrange: Mémoires extraits des recueils de l'Académie royale des sciences et belles-lettres de Berlin (en francés). Gauthier-Villars: 619.
- ^ Gauss, Carl Friedrich (1877). "Theoria atracciónis corporum sphaeroidicorum ellipticorum homogeneorum Methodo nova tractata" [La teoría de la atracción de cuerpos elípticos esferoidales homogéneos tratada mediante un nuevo método]. En Schering, Ernst Christian Julius ; Brendel, Martín (eds.). Carl Friedrich Gauss Werke [ Obras de Carl Friedrich Gauss ] (en latín y alemán). vol. 5 (2ª ed.). Gedruckt in der Dieterichschen Universitätsdruckerei (WF Kaestner). págs. 2–22.Gauss menciona la proposición XCI de los Principia de Newton sobre cómo encontrar la fuerza ejercida por una esfera sobre un punto en cualquier parte a lo largo de un eje que pasa por la esfera.
- ^ Halliday, David; Resnick, Robert (1970). Fundamentos de física . John Wiley & Sons. págs. 452–453.
- ^ Serway, Raymond A. (1996). Física para científicos e ingenieros con Física moderna (4ª ed.). pág. 687.
- ^ ab Grant, IS; Phillips, WR (2008). Electromagnetismo . Manchester Physics (2.ª ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- ^ Matthews, Paul (1998). Cálculo vectorial . Springer. ISBN 3-540-76180-2.
- ^ Fedosin, Sergey G. (2019). "Sobre la representación covariante de ecuaciones integrales del campo electromagnético". Progress in Electromagnetics Research C . 96 : 109–122. arXiv : 1911.11138 . Código Bibliográfico :2019arXiv191111138F. doi :10.2528/PIERC19062902. S2CID 208095922.
- ^ Véase, por ejemplo, Griffiths, David J. (2013). Introducción a la electrodinámica (4.ª ed.). Prentice Hall. pág. 50.o Jackson, John David (1999). Electrodinámica clásica (3.ª ed.). John Wiley & Sons. pág. 35.
Referencias
- Gauss, Carl Friedrich (1867). Trabajo Banda 5 .Versión digital
- Jackson, John David (1998). Electrodinámica clásica (3.ª ed.). Nueva York: Wiley. ISBN 0-471-30932-X.David J. Griffiths (6ª ed.)
Enlaces externos
 Medios relacionados con la Ley de Gauss en Wikimedia Commons
Medios relacionados con la Ley de Gauss en Wikimedia Commons- Serie de conferencias en video del MIT (30 conferencias de 50 minutos): Electricidad y magnetismo, impartidas por el profesor Walter Lewin .
- Sección sobre la ley de Gauss en un libro de texto en línea Archivado el 27 de mayo de 2010 en Wayback Machine.
- MISN-0-132 Ley de Gauss para simetría esférica ( archivo PDF ) por Peter Signell para el Proyecto PHYSNET.
- MISN-0-133 Ley de Gauss aplicada a distribuciones de carga cilíndricas y planas (archivo PDF) por Peter Signell para el Proyecto PHYSNET.



































































