Electrostática

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Aislante Permitividad Polarización Energía potencial Electricidad estática Triboelectricidad
Magnetostática Ley de Ampère Ley de Biot-Savart Ley magnética de Gauss Dipolo magnético Campo magnético Flujo magnético Potencial escalar magnético Potencial vectorial magnético Magnetización Permeabilidad Regla de la mano derecha
Electrodinámica Radiación de frenado Radiación ciclotrónica Corriente de desplazamiento Corriente de Foucault Campo electromagnético Inducción electromagnética Pulso electromagnético Radiación electromagnética Ley de Faraday Ecuaciones de Jefimenko Fórmula de Larmor Ley de Lenz Potencial de Liénard-Wiechert Ecuaciones de Londres Fuerza de Lorentz Ecuaciones de Maxwell Tensor de Maxwell Vector de Poynting Radiación de sincrotrón
Red eléctrica Corriente alterna Capacidad Densidad de corriente Corriente continua Corriente eléctrica Energía eléctrica Electrólisis Fuerza electromotriz Impedancia Inductancia Calentamiento Joule Leyes de Kirchhoff Análisis de red Ley de Ohm Circuito paralelo Resistencia Cavidades resonantes Circuito en serie Voltaje Vatio Guías de ondas
Circuito magnético Motor de corriente alterna Motor de corriente continua Maquina electrica Motor eléctrico Condensador giratorio Motor de inducción Motor lineal Fuerza magnetomotriz Permeancia Renuencia (compleja) Renuencia (real) Rotor Estator Transformador
Formulación covariante Tensor electromagnético Electromagnetismo y relatividad especial Cuatro corrientes Cuatro potenciales Descripciones matemáticas Ecuaciones de Maxwell en el espacio-tiempo curvo Electromagnetismo relativista Tensor de estrés-energía
Científicos Amperio Biot Culombio David Einstein Faraday Fizeau Gauss Lado pesado Helmholtz Enrique Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Pescado Poynting Ritchie Sabor Cantante Piedras preciosas Tesla Thomson Vuelta Weber Wiechert
en a mi

La electrostática es una rama de la física que estudia las cargas eléctricas de movimiento lento o estacionarias .

Desde la época clásica se sabe que algunos materiales, como el ámbar , atraen partículas ligeras tras frotarlos . La palabra griega para ámbar, ἤλεκτρον ( ḗlektron ), fue así el origen de la palabra electricidad . Los fenómenos electrostáticos surgen de las fuerzas que ejercen entre sí las cargas eléctricas. Dichas fuerzas se describen mediante la ley de Coulomb .

Hay muchos ejemplos de fenómenos electrostáticos, desde aquellos tan simples como la atracción de un envoltorio de plástico hacia la mano después de sacarlo de un paquete, hasta la explosión aparentemente espontánea de silos de granos, el daño de componentes electrónicos durante la fabricación y el funcionamiento de fotocopiadoras e impresoras láser .

El modelo electrostático predice con precisión los fenómenos eléctricos en casos "clásicos" en los que las velocidades son bajas y el sistema es macroscópico, por lo que no intervienen efectos cuánticos. También desempeña un papel en la mecánica cuántica, donde también es necesario incluir términos adicionales.

La ley de Coulomb establece que: ^[5]

La magnitud de la fuerza electrostática de atracción o repulsión entre dos cargas puntuales es directamente proporcional al producto de las magnitudes de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas.

La fuerza se ejerce a lo largo de la línea recta que las une. Si las dos cargas tienen el mismo signo, la fuerza electrostática entre ellas es repulsiva; si tienen signos diferentes, la fuerza entre ellas es atractiva.

Si es la distancia (en metros ) entre dos cargas, entonces la fuerza entre dos cargas puntuales y es:${\displaystyle r}$${\displaystyle Q}$${\displaystyle q}$

${\displaystyle F={1 \over 4\pi \varepsilon _{0}}{|Qq| \over r^{2}},}$

donde ε ₀ =8.854 187 8188 (14) × 10 ⁻¹²  F⋅m ⁻¹ ‍ [ ^6] es la permitividad del vacío . ^[7]

La unidad SI de ε ₀ es equivalentemente A ² ⋅ s ⁴ ⋅kg ⁻¹ ⋅m ⁻³ o C ² ⋅ N ⁻¹ ⋅m ⁻² o F ⋅m ⁻¹ .

El campo eléctrico, en unidades de Newtons por Coulomb o voltios por metro, es un campo vectorial que se puede definir en todas partes, excepto en la ubicación de cargas puntuales (donde diverge hasta el infinito). ^[8] Se define como la fuerza electrostática sobre una pequeña carga de prueba hipotética en el punto debido a la ley de Coulomb, dividida por la carga${\displaystyle \mathbf {E} }$${\displaystyle \mathbf {,} }$${\displaystyle q}$

${\displaystyle \mathbf {E} ={\mathbf {F} \over q}}$

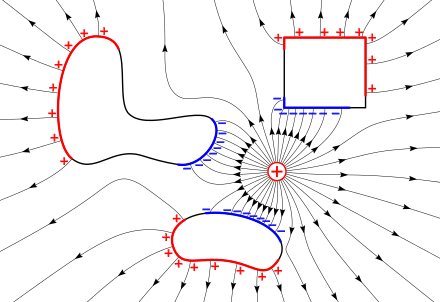
Las líneas de campo eléctrico son útiles para visualizar el campo eléctrico. Las líneas de campo comienzan en una carga positiva y terminan en una carga negativa. Son paralelas a la dirección del campo eléctrico en cada punto, y la densidad de estas líneas de campo es una medida de la magnitud del campo eléctrico en cualquier punto dado.

Una colección de partículas de carga , ubicadas en puntos (llamados puntos fuente ) genera el campo eléctrico en (llamado punto de campo ) de: ^[8]${\displaystyle n}$${\displaystyle q_{i}}$${\displaystyle \mathbf {r} _{i}}$${\displaystyle \mathbf {r} }$

${\displaystyle \mathbf {E} (\mathbf {r} )={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{{\hat {\mathbf {r} }}_{i} \over {|\mathbf {r} _{i}|}^{2}}={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{\mathbf {r} _{i} \over {|\mathbf {r} _{i}|}^{3}},}$

donde es el vector de desplazamiento desde un punto de origen hasta el punto de campo , y es un vector unitario que indica la dirección del campo. Para una sola carga puntual, , en el origen, la magnitud de este campo eléctrico es y apunta en dirección opuesta a esa carga si es positiva. El hecho de que la fuerza (y, por lo tanto, el campo) se pueda calcular sumando todas las contribuciones debidas a partículas de origen individuales es un ejemplo del principio de superposición . El campo eléctrico producido por una distribución de cargas viene dado por la densidad de carga volumétrica y se puede obtener convirtiendo esta suma en una integral triple :${\textstyle \mathbf {r} _{i}=\mathbf {r} -\mathbf {r} _{i}}$ ${\displaystyle \mathbf {r} _{i}}$ ${\displaystyle \mathbf {r} }$${\textstyle {\hat {\mathbf {r} }}_{i}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathbf {r} _{i}}{|\mathbf {r} _{i}|}}}$${\displaystyle q}$${\displaystyle E=q/4\pi \varepsilon _{0}r^{2}}$ ${\displaystyle \rho (\mathbf {r} )}$

${\displaystyle \mathbf {E} (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\iiint \,\rho (\mathbf {r} '){\mathbf {r} ' \over {|\mathbf {r} '|}^{3}}\mathrm {d} ^{3}|\mathbf {r} '|}$

La ley de Gauss ^{[9] [10]} establece que "el flujo eléctrico total a través de cualquier superficie cerrada en el espacio libre de cualquier forma dibujada en un campo eléctrico es proporcional a la carga eléctrica total encerrada por la superficie". Muchos problemas numéricos se pueden resolver considerando una superficie gaussiana alrededor de un cuerpo. Matemáticamente, la ley de Gauss toma la forma de una ecuación integral:

${\displaystyle \Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={Q_{\text{enclosed}} \over \varepsilon _{0}}=\int _{V}{\rho \over \varepsilon _{0}}\mathrm {d} ^{3}r,}$

donde es un elemento de volumen. Si la carga se distribuye sobre una superficie o a lo largo de una línea, reemplácela por o . El teorema de la divergencia permite escribir la ley de Gauss en forma diferencial:${\displaystyle \mathrm {d} ^{3}r=\mathrm {d} x\ \mathrm {d} y\ \mathrm {d} z}$${\displaystyle \rho \,\mathrm {d} ^{3}r}$${\displaystyle \sigma \,\mathrm {d} A}$${\displaystyle \lambda \,\mathrm {d} \ell }$

${\displaystyle \nabla \cdot \mathbf {E} ={\rho \over \varepsilon _{0}}.}$

¿Dónde está el operador de divergencia ?${\displaystyle \nabla \cdot }$

La definición de potencial electrostático, combinada con la forma diferencial de la ley de Gauss (arriba), proporciona una relación entre el potencial Φ y la densidad de carga ρ :

${\displaystyle {\nabla }^{2}\phi =-{\rho \over \varepsilon _{0}}.}$

Esta relación es una forma de la ecuación de Poisson . ^[11] En ausencia de carga eléctrica desapareada, la ecuación se convierte en la ecuación de Laplace :

${\displaystyle {\nabla }^{2}\phi =0,}$

La validez de la aproximación electrostática se basa en el supuesto de que el campo eléctrico es irrotacional :

${\displaystyle \nabla \times \mathbf {E} =0.}$

De la ley de Faraday , esta suposición implica la ausencia o casi ausencia de campos magnéticos variables en el tiempo:

${\displaystyle {\partial \mathbf {B} \over \partial t}=0.}$

En otras palabras, la electrostática no requiere la ausencia de campos magnéticos o corrientes eléctricas. Más bien, si existen campos magnéticos o corrientes eléctricas , no deben cambiar con el tiempo, o en el peor de los casos, deben cambiar con el tiempo sólo muy lentamente . En algunos problemas, tanto la electrostática como la magnetostática pueden ser necesarias para predicciones precisas, pero el acoplamiento entre las dos puede ignorarse. La electrostática y la magnetostática pueden verse como límites galileanos no relativistas para el electromagnetismo. ^[12] Además, la electrostática convencional ignora los efectos cuánticos que deben agregarse para una descripción completa. ^{[8] : 2}

Como el campo eléctrico es irrotacional , es posible expresarlo como el gradiente de una función escalar, , llamada potencial electrostático (también conocido como voltaje ). Un campo eléctrico, , apunta desde regiones de alto potencial eléctrico a regiones de bajo potencial eléctrico, expresado matemáticamente como${\displaystyle \phi }$${\displaystyle E}$

${\displaystyle \mathbf {E} =-\nabla \phi .}$

El teorema del gradiente se puede utilizar para establecer que el potencial electrostático es la cantidad de trabajo por unidad de carga necesaria para mover una carga de un punto a otro con la siguiente integral de línea :${\displaystyle a}$${\displaystyle b}$

${\displaystyle -\int _{a}^{b}{\mathbf {E} \cdot \mathrm {d} \mathbf {\ell } }=\phi (\mathbf {b} )-\phi (\mathbf {a} ).}$

A partir de estas ecuaciones, vemos que el potencial eléctrico es constante en cualquier región en la que el campo eléctrico desaparece (como ocurre dentro de un objeto conductor).

La energía potencial de una partícula de prueba , , se puede calcular a partir de una integral lineal del trabajo, . Integramos desde un punto en el infinito y suponemos que una colección de partículas de carga , ya están situadas en los puntos . Esta energía potencial (en julios ) es:${\displaystyle U_{\mathrm {E} }^{\text{single}}}$${\displaystyle q_{n}\mathbf {E} \cdot \mathrm {d} \mathbf {\ell } }$${\displaystyle N}$${\displaystyle Q_{n}}$${\displaystyle \mathbf {r} _{i}}$

${\displaystyle U_{\mathrm {E} }^{\text{single}}=q\phi (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\frac {Q_{i}}{\left\|{\mathcal {\mathbf {R} _{i}}}\right\|}}}$

donde es la distancia de cada carga a la carga de prueba , que se encuentra en el punto , y es el potencial eléctrico que habría en si la carga de prueba no estuviera presente. Si solo hay dos cargas presentes, la energía potencial es . La energía potencial eléctrica total debida a un conjunto de N cargas se calcula juntando estas partículas una a la vez :${\displaystyle \mathbf {\mathcal {R_{i}}} =\mathbf {r} -\mathbf {r} _{i}}$${\displaystyle Q_{i}}$ ${\displaystyle q}$${\displaystyle \mathbf {r} }$${\displaystyle \phi (\mathbf {r} )}$${\displaystyle \mathbf {r} }$${\displaystyle Q_{1}Q_{2}/(4\pi \varepsilon _{0}r)}$

${\displaystyle U_{\mathrm {E} }^{\text{total}}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{j=1}^{N}Q_{j}\sum _{i=1}^{j-1}{\frac {Q_{i}}{r_{ij}}}={\frac {1}{2}}\sum _{i=1}^{N}Q_{i}\phi _{i},}$

donde la siguiente suma de j = 1 a N , excluye i = j :

${\displaystyle \phi _{i}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{\stackrel {j=1}{j\neq i}}^{N}{\frac {Q_{j}}{r_{ij}}}.}$

Este potencial eléctrico es el que se mediría si faltara la carga. Obviamente, esta fórmula excluye la energía (infinita) que se requeriría para ensamblar cada carga puntual a partir de una nube de carga dispersa. La suma de cargas se puede convertir en una densidad de carga integral utilizando la siguiente fórmula :${\displaystyle \phi _{i}}$${\displaystyle \mathbf {r} _{i}}$${\displaystyle Q_{i}}$${\textstyle \sum (\cdots )\rightarrow \int (\cdots )\rho \,\mathrm {d} ^{3}r}$

${\displaystyle U_{\mathrm {E} }^{\text{total}}={\frac {1}{2}}\int \rho (\mathbf {r} )\phi (\mathbf {r} )\,\mathrm {d} ^{3}r={\frac {\varepsilon _{0}}{2}}\int \left|{\mathbf {E} }\right|^{2}\,\mathrm {d} ^{3}r,}$

Esta segunda expresión para la energía electrostática utiliza el hecho de que el campo eléctrico es el gradiente negativo del potencial eléctrico, así como las identidades del cálculo vectorial de una manera que se asemeja a la integración por partes . Estas dos integrales para la energía del campo eléctrico parecen indicar dos fórmulas mutuamente excluyentes para la densidad de energía electrostática, a saber y ; producen valores iguales para la energía electrostática total solo si ambas se integran en todo el espacio.${\textstyle {\frac {1}{2}}\rho \phi }$${\textstyle {\frac {1}{2}}\varepsilon _{0}E^{2}}$

En un conductor , una carga superficial experimentará una fuerza en presencia de un campo eléctrico . Esta fuerza es el promedio del campo eléctrico discontinuo en la carga superficial. Este promedio en términos del campo justo fuera de la superficie asciende a:

${\displaystyle P={\frac {\varepsilon _{0}}{2}}E^{2},}$

Esta presión tiende a atraer al conductor hacia el campo, independientemente del signo de la carga superficial.

• Electromagnetismo  – Interacción fundamental entre partículas cargadas
• Generador electrostático , máquinas que crean electricidad estática.
• Inducción electrostática , separación de cargas debido a campos eléctricos.
• Permitividad y permitividad relativa , la polarizabilidad eléctrica de los materiales.
• Cuantización de carga , las unidades de carga transportadas por electrones o protones.
• Electricidad estática , carga estacionaria acumulada en un material.
• Efecto triboeléctrico , separación de cargas por deslizamiento o contacto.

• Hermann A. Haus; James R. Melcher (1989). Campos electromagnéticos y energía . Englewood Cliffs, Nueva Jersey: Prentice-Hall. ISBN 0-13-249020-X.
• Halliday, David; Robert Resnick; Kenneth S. Krane (1992). Física . Nueva York: John Wiley & Sons. ISBN 0-471-80457-6.
• Griffiths, David J. (1999). Introducción a la electrodinámica . Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-805326-X.

Wikisource tiene el texto del artículo de la Encyclopædia Britannica de 1911 " Electrostática ".

• Medios relacionados con la electrostática en Wikimedia Commons

Busque electrostática en Wikcionario, el diccionario libre.

• Las conferencias de física de Feynman, vol. II, cap. 4: electrostática
• Introducción a la electrostática: Las cargas puntuales se pueden tratar como una distribución utilizando la función delta de Dirac

Materiales de aprendizaje relacionados con la electrostática en Wikiversidad