5
Número entero 5
Número natural
← 456 →
Cardenalcinco
Ordinal5º (quinto)
Sistema de numeraciónquinario
Factorizaciónprincipal
Principal3º
Divisores1, 5
Número griegoE´
Número romanoV, v
Prefijo griegopenta-/pent-
Prefijo latinoquinque-/quinqu-/quint-
Binario101 2
Ternario12 3
Senador5 6
Octal5 8
Duodecimal5 12
Hexadecimal5 16
Griegoε (o Ε)
Árabe , kurdo5
Persa , sindhi , urdu5
Dios mio፭
bengalí৫
Canarés೫
punjabiYo
Número chinoYo
armenioɴ
DevanagariA mí
hebreoYo
Jemer៥
Télugu౫
Malabar൫
Tamil௫
tailandés๕
Número babilónico𒐙
Jeroglífico egipcio , vara de contar china|||||
Numerales mayas𝋥
Código morse.....

5 ( cinco ) es un número , numeral y dígito . Es el número natural y cardinal que sigue al 4 y precede al 6 , y es un número primo .

Los humanos, y muchos otros animales, tienen cinco dedos en sus extremidades .

Matemáticas

El primer triple pitagórico

5 es un primo de Fermat , un exponente primo de Mersenne , así como un número de Fibonacci . 5 es el primer número congruente , así como la longitud de la hipotenusa del triángulo rectángulo de lados enteros más pequeño , que forma parte del triple pitagórico más pequeño ( 3 , 4 , 5). [1]

5 es el primer primo seguro , [2] y el primer primo bueno . [3] 11 forma el primer par de primos atractivos con 5. [4] 5 es el segundo primo de Fermat , de un total de cinco primos de Fermat conocidos. [5] 5 es también el primero de tres primos de Wilson conocidos (5, 13, 563). [6]

Geometría

Una figura con cinco lados se llama pentágono . El pentágono es el primer polígono regular que no cubre el plano con copias de sí mismo. Es la cara más grande que puede tener cualquiera de los cinco sólidos platónicos regulares tridimensionales .

Una cónica se determina usando cinco puntos de la misma manera que se necesitan dos puntos para determinar una línea . [7] Un pentagrama , o poligrama de cinco puntas , es un polígono estrellado construido conectando algunos no adyacentes de un pentágono regular como bordes autointersecantes . [8] La geometría interna del pentágono y el pentagrama (representado por su símbolo de Schläfli {5/2} ) aparece de manera prominente en los mosaicos de Penrose . Los pentagramas son facetas dentro de los poliedros estelares de Kepler-Poinsot y los policoros estelares de Schläfli-Hess .

Hay cinco sólidos platónicos regulares: el tetraedro , el cubo , el octaedro , el dodecaedro y el icosaedro . [9]

El número cromático del plano es el número mínimo de colores necesarios para colorear el plano de tal manera que ningún par de puntos a una distancia de 1 tenga el mismo color. [10] Cinco es un número menor para el número cromático del plano, pero esto puede depender de la elección de los axiomas de la teoría de conjuntos : [11]

El plano contiene un total de cinco redes de Bravais , o matrices de puntos definidos por operaciones de traslación discretas . Los mosaicos uniformes del plano se generan a partir de combinaciones de solo cinco polígonos regulares. [12]

Geometría de dimensiones superiores

Un hipertetraedro , o 5-celda, es el análogo en 4 dimensiones del tetraedro . Tiene cinco vértices. Su proyección ortográfica es homomórfica al grupo K 5. [13] : p.120 

Existen cinco familias fundamentales de grupos puntuales de simetría especular en 4 dimensiones . También existen 5 grupos hiperbólicos compactos de Coxeter , o 4-prismas , de rango 5, cada uno de los cuales genera panales uniformes en el 4-espacio hiperbólico como permutaciones de anillos de los diagramas de Coxeter. [14]

El policoronte cuatridimensional de cinco células es el policoron regular más simple .

Álgebra

El cuadrado mágico no trivial más pequeño

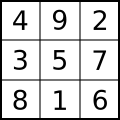
5 es el valor de la celda central del primer cuadrado mágico normal no trivial , llamado cuadrado de Luoshu . Todos los números enteros se pueden expresar como la suma de cinco cuadrados distintos de cero . [15] [16] Hay cinco clases de permutaciones de Ramsey infinitas y numerables . [17] : p.4  Se conjetura que 5 es el único número impar e intocable ; si este es el caso, entonces cinco será el único número primo impar que no sea la base de un árbol de alícuotas . [18] norte ≥ 34 {\displaystyle n\geq 34}

Este diagrama muestra las relaciones subcocientes de los veintiséis grupos esporádicos ; los cinco grupos de Mathieu forman la clase más simple (coloreada en rojo).).

Se supone que todo número impar mayor que cinco puede expresarse como la suma de tres números primos; Helfgott ha proporcionado una prueba de esto [19] (también conocida como la conjetura de Goldbach impar ) que ya es ampliamente reconocida por los matemáticos, ya que todavía está en revisión por pares . Por otro lado, todo número impar mayor que uno es la suma de, como máximo, cinco números primos (como límite inferior). [20]

Problema sin resolver en matemáticas :
¿Es el 5 el único número impar e intocable?
(más problemas sin resolver en matemáticas)

Teoría de grupos

En teoría de grafos , todos los grafos con cuatro o menos vértices son planos , sin embargo, hay un grafo con cinco vértices que no lo es: K 5 , el grafo completo con cinco vértices. Por el teorema de Kuratowski , un grafo finito es plano si y solo si no contiene un subgrafo que sea una subdivisión de , o K 3,3 , el grafo de utilidad . [21]

Existen cinco álgebras de Lie excepcionales y complejas . Los cinco grupos de Mathieu constituyen la primera generación de la feliz familia de los grupos esporádicos . También son los primeros cinco grupos esporádicos que se han descrito . [22] : p.54  Un centralizador de un elemento de orden 5 dentro del grupo esporádico más grande surge del producto entre el grupo esporádico de Harada-Norton y un grupo de orden 5. [23] [24] F 1 {\displaystyle \mathrm {F_{1}} } yo norte {\displaystyle \mathrm {HN}}

Lista de cálculos básicos

Multiplicación1234567891011121314151617181920
5 × x5101520253035404550556065707580859095100
División123456789101112131415
5 ÷ x52.51.6​1.2510,8 30.714285​0,6250.5​0,50.45​0,41 60.384615​0,3 5714280.3​
x ÷50,20,40.60,81.21.41.61.822.22.42.62.83
Exponenciación123456789101112131415
5x​5251256253125156257812539062519531259765625488281252441406251220703125610351562530517578125
x5​13224310247776168073276859049100000161051248832371293537824759375

Evolución del dígito árabe

La evolución del dígito occidental moderno para el número cinco se remonta al sistema numérico indio , donde en algunas versiones anteriores, el número se parecía a variaciones del número cuatro, en lugar del "5" (como se representa hoy). Los imperios Kushana y Gupta en lo que hoy es la India tenían entre sí varias formas que no guardaban semejanza con el dígito moderno. Más tarde, las tradiciones árabes transformaron el dígito de varias maneras, produciendo formas que todavía eran similares al numeral para cuatro, con similitudes con el numeral para tres, pero aún diferentes al cinco moderno. [25] Fue a partir de esos dígitos que los europeos finalmente idearon el 5 moderno (representado en los escritos de Durero, por ejemplo).

Si bien la forma del carácter del dígito 5 tiene un ascendente en la mayoría de las tipografías modernas , en las tipografías con figuras de texto el glifo suele tener un descendente , como, por ejemplo, en.

En la pantalla de siete segmentos de una calculadora y un reloj digital, se representa mediante cinco segmentos en cuatro vueltas sucesivas de arriba a abajo, girando primero en sentido contrario a las agujas del reloj, luego en el sentido de las agujas del reloj y viceversa. Es uno de los tres números, junto con el 4 y el 6, en los que el número de segmentos coincide con el número.

Otros campos

Astronomía

Hay cinco puntos lagrangianos en un sistema de dos cuerpos.

Biología

Generalmente se considera que hay cinco sentidos (en términos generales ); los cinco sabores básicos son dulce , salado , agrio , amargo y umami . [26] Casi todos los anfibios, reptiles y mamíferos que tienen dedos en las manos o en los pies tienen cinco de ellos en cada extremidad. [27] Cinco es el número de apéndices en la mayoría de las estrellas de mar , que exhiben pentamerismo . [28]

Computación

5 es el código ASCII del carácter de consulta , que se abrevia como ENQ. [29]

Literatura

Poesía

Un pentámetro es un verso con cinco pies repetidos por línea; el pentámetro yámbico fue la forma más destacada utilizada por William Shakespeare . [30]

Música

La notación musical moderna utiliza un pentagrama musical formado por cinco líneas horizontales. [31] Una escala con cinco notas por octava se llama escala pentatónica . [32] Una quinta perfecta es la armonía más consonante y es la base de la mayoría de los sistemas de afinación occidentales. [33] En armónicos , el quinto parcial (o cuarto sobretono ) de una fundamental tiene una relación de frecuencia de 5:1 con la frecuencia de esa fundamental. Esta relación corresponde al intervalo de 2 octavas más una tercera mayor pura. Por lo tanto, el intervalo de 5:4 es el intervalo de la tercera pura. Un acorde de tríada mayor cuando se toca en entonación justa (el caso más frecuente en un conjunto vocal a capela), contendrá dicha tercera mayor pura.

Cinco es el número más bajo posible que puede ser el número superior de un compás con un metro asimétrico .

Religión

judaísmo

El Libro de los Números es uno de los cinco libros de la Torá ; los otros son los libros de Génesis , Éxodo , Levítico y Deuteronomio . Se los llama colectivamente los Cinco Libros de Moisés , el Pentateuco ( en griego , "cinco contenedores", en referencia a los estuches de pergaminos en los que se guardaban los libros) o Humash ( en hebreo , חומש , "quinto"). [34] El Khamsa , un antiguo símbolo con forma de mano con cuatro dedos y un pulgar, es utilizado como amuleto protector por los judíos ; ese mismo símbolo también es muy popular en la cultura árabe , conocido por proteger de la envidia y el mal de ojo . [35]

cristianismo

Tradicionalmente hay cinco heridas de Jesucristo en el cristianismo : las heridas de los clavos en las dos manos de Cristo, las heridas de los clavos en los dos pies de Cristo y la herida de la lanza de Cristo (respectivamente en las cuatro extremidades del cuerpo y la cabeza). [36]

islam

Los cinco pilares del Islam . [37] La ​​estrella simple de cinco puntas ☆ es una de las cinco utilizadas en los mosaicos islámicos Girih . [38]

Misticismo

Gnosticismo

El número cinco era un número simbólico importante en el maniqueísmo , donde los seres celestiales, los conceptos y otros solían agruparse en grupos de cinco.

Alquimia

Según los filósofos griegos antiguos como Aristóteles , el universo está formado por cinco elementos clásicos : agua , tierra , aire , fuego y éter . Este concepto fue adoptado posteriormente por los alquimistas medievales y más recientemente por los practicantes de religiones neopaganas como la Wicca . Hay cinco elementos en el universo según la cosmología hindú : dharti, agni, jal, vayu evam akash (tierra, fuego, agua, aire y espacio, respectivamente). En la tradición del este de Asia , hay cinco elementos: agua , fuego , tierra , madera y metal . [39] Los nombres japoneses para los días de la semana , de martes a sábado , provienen de estos elementos a través de la identificación de los elementos con los cinco planetas visibles a simple vista . [40] Además, el calendario japonés tradicional tiene un ciclo semanal de cinco días que todavía se puede observar en calendarios mixtos impresos que combinan nombres occidentales, chino-budistas y japoneses para cada día de la semana. También hay cinco elementos en el Wuxing chino tradicional . [41]

Quintaesencia , que significa "quinto elemento", se refiere al elusivo quinto elemento que completa los cuatro elementos básicos (agua, fuego, aire y tierra), como una unión de estos. [42] El pentagrama , o estrella de cinco puntas, tiene un significado místico en varios sistemas de creencias, incluidos el baháʼí , el cristianismo , la masonería , el satanismo , el taoísmo , el thelema y la wicca .

Campos varios

Los cincos de los cuatro palos en las cartas de juego
  • "Dame cinco" es una frase común que se usa antes de un " choca esos cinco" .
  • Los Juegos Olímpicos tienen como símbolo cinco anillos entrelazados, que representan el número de continentes habitados representados por los olímpicos (Europa, Asia, África, Australia y Oceanía, y las Américas). [43]
  • El número de puntos en un quincuncio . [44]

Véase también

Notas

  1. ^ Sloane, N. J. A. (ed.). "Secuencia A003273 (Números congruentes)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 1 de junio de 2016 .
  2. ^ Sloane, N. J. A. (ed.). "Secuencia A005385 (Primos seguros p: (p-1)/2 también es primo)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 14 de febrero de 2023 .
  3. ^ Sloane, N. J. A. (ed.). "Secuencia A028388 (buenos primos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 1 de junio de 2016 .
  4. ^ Sloane, N. J. A. (ed.). "Secuencia A023201 (Primos p tales que p + 6 también es primo. (El menor de un par de primos atractivos.))". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 14 de enero de 2023 .
  5. ^ Sloane, N. J. A. (ed.). "Secuencia A019434 (primos de Fermat)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 21 de julio de 2022 .
  6. ^ Sloane, N. J. A. (ed.). "Secuencia A007540 (primos de Wilson: primos p de modo que (p-1)! es congruente -1 (mod p^2).)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 6 de septiembre de 2023 .
  7. ^ Dixon, AC (marzo de 1908). "La cónica a través de cinco puntos dados". The Mathematical Gazette . 4 (70). The Mathematical Association: 228–230. doi :10.2307/3605147. JSTOR  3605147. S2CID  125356690.
  8. ^ Sloane, N. J. A. (ed.). "Secuencia A307681 (Diferencia entre el número de lados y el número de diagonales de un n-gono convexo)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
  9. ^ Bryan Bunch, El reino de los números infinitos . Nueva York: WH Freeman & Company (2000): 61
  10. ^ de Grey, Aubrey DNJ (2018). "El número cromático del plano es al menos 5". Geombinatorics . 28 : 5–18. arXiv : 1804.02385 . MR  3820926. S2CID  119273214.
  11. ^ Exoo, Geoffrey; Ismailescu, Dan (2020). "El número cromático del plano es al menos 5: una nueva prueba". Geometría discreta y computacional . 64 . Nueva York, NY: Springer : 216–226. arXiv : 1805.00157 . doi :10.1007/s00454-019-00058-1. MR  4110534. S2CID  119266055. Zbl  1445.05040.
  12. ^ Grünbaum, Branko ; Shepard, Geoffrey (noviembre de 1977). "Teselas mediante polígonos regulares" (PDF) . Mathematics Magazine . 50 (5). Taylor & Francis, Ltd.: 227–236. doi :10.2307/2689529. JSTOR  2689529. S2CID  123776612. Zbl  0385.51006.
  13. ^ HSM Coxeter (1973). Politopos regulares (3.ª ed.). Nueva York: Dover Publications, Inc., págs. 1–368. ISBN 978-0-486-61480-9.
  14. ^ McMullen, Peter ; Schulte, Egon (2002). Resumen de politopos regulares . Enciclopedia de matemáticas y sus aplicaciones. Vol. 92. Cambridge: Cambridge University Press. págs. 162–164. doi :10.1017/CBO9780511546686. ISBN 0-521-81496-0. Sr.  1965665. S2CID  115688843.
  15. ^ Niven, Ivan ; Zuckerman, Herbert S.; Montgomery, Hugh L. (1980). Introducción a la teoría de números (quinta edición). Nueva York, NY: John Wiley . pp. 144, 145. ISBN. 978-0-19-853171-5.
  16. ^ Sloane, N. J. A. (ed.). "Secuencia A047701 (Todos los números positivos que no son la suma de 5 cuadrados distintos de cero)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS . Consultado el 20 de septiembre de 2023 .
    Sólo doce números enteros hasta 33 no pueden expresarse como la suma de cinco cuadrados distintos de cero: {1, 2, 3, 4, 6, 7, 9, 10, 12, 15, 18, 33} donde 2, 3 y 7 son los únicos primos sin expresión.
  17. ^ Böttcher, Julia ; Foniok, Jan (2013). "Propiedades de Ramsey de las permutaciones". Revista Electrónica de Combinatoria . 20 (1): P2. arXiv : 1103.5686v2 . doi :10.37236/2978. S2CID  17184541. Zbl  1267.05284.
  18. ^ Pomerance, Carl; Yang, Hee-Sung (14 de junio de 2012). "Sobre números intocables y problemas relacionados" (PDF) . math.dartmouth.edu . Dartmouth College : 1. S2CID  30344483.Clasificación de materias de matemáticas 2010. 11A25, 11Y70, 11Y16.
  19. ^ Helfgott, Harald Andres (2014). "El problema ternario de Goldbach" (PDF) . En Jang, Sun Young (ed.). Actas del Congreso Internacional de Matemáticos de Seúl . Vol. 2. Seúl, KOR: Kyung Moon SA. págs. 391–418. ISBN 978-89-6105-805-6.OCLC 913564239  .
  20. ^ Tao, Terence (marzo de 2014). "Todo número impar mayor que 1 tiene una representación que es la suma de cinco primos como máximo" (PDF) . Matemáticas de la computación . 83 (286): 997–1038. doi :10.1090/S0025-5718-2013-02733-0. MR  3143702. S2CID  2618958.
  21. ^ Burnstein, Michael (1978). "Teorema de Kuratowski-Pontrjagin sobre grafos planares". Journal of Combinatorial Theory . Serie B. 24 (2): 228–232. doi : 10.1016/0095-8956(78)90024-2 .
  22. ^ Robert L. Griess, Jr. (1998). Doce Grupos Esporádicos . Monografías de Springer en Matemáticas. Berlín: Springer-Verlag. págs. 1-169. doi :10.1007/978-3-662-03516-0. ISBN 978-3-540-62778-4. SEÑOR  1707296. S2CID  116914446. Zbl  0908.20007.
  23. ^ Lux, Klaus; Noeske, Felix; Ryba, Alexander JE (2008). "Los caracteres 5-modulares del grupo esporádico simple Harada–Norton HN y su grupo de automorfismos HN.2". Journal of Algebra . 319 (1). Ámsterdam: Elsevier : 320–335. doi : 10.1016/j.jalgebra.2007.03.046 . MR  2378074. S2CID  120706746. Zbl  1135.20007.
  24. ^ Wilson, Robert A. (2009). "Los subgrupos locales impares del Monstruo". Revista de la Sociedad Matemática Australiana (Serie A) . 44 (1). Cambridge: Cambridge University Press : 12–13. doi : 10.1017/S1446788700031323 . MR  0914399. S2CID  123184319. Zbl  0636.20014.
  25. ^ Georges Ifrah, La historia universal de los números: desde la prehistoria hasta la invención de la computadora , trad. David Bellos et al. Londres: The Harvill Press (1998): 394, fig. 24.65
  26. ^ Marcus, Jacqueline B. (15 de abril de 2013). Nutrición culinaria: la ciencia y la práctica de la cocina saludable. Academic Press. pág. 55. ISBN 978-0-12-391883-3Hay cinco sabores básicos: dulce, salado, agrio, amargo y umami ...
  27. ^ Kisia, SM (2010), Vertebrados: Estructuras y funciones, sistemas biológicos en vertebrados, CRC Press, pág. 106, ISBN 978-1-4398-4052-8La extremidad típica de los tetrápodos es la extremidad pentadáctila (del griego penta, cinco) , que tiene cinco dedos. Los tetrápodos evolucionaron a partir de un ancestro que tenía extremidades con cinco dedos. ... Aunque el número de dígitos en diferentes vertebrados puede variar de cinco, los vertebrados se desarrollan a partir de una etapa embrionaria de cinco dígitos.
  28. ^ Cinalli, G.; Maixner, WJ; Sainte-Rose, C. (6 de diciembre de 2012). Hidrocefalia pediátrica. Springer Science & Business Media. pág. 19. ISBN 978-88-470-2121-1Se cree que los cinco apéndices de la estrella de mar son homólogos de cinco botones humanos .
  29. ^ Pozrikidis, Constantine (17 de septiembre de 2012). XML en computación científica. CRC Press. pág. 209. ISBN 978-1-4665-1228-3. 5 5 005 ENQ (consulta)
  30. ^ Veith (Jr.), Gene Edward; Wilson, Douglas (2009). Omnibus IV: El mundo antiguo. Veritas Press. pág. 52. ISBN 978-1-932168-86-0Los versos acentuales-silábicos más comunes son los versos yámbicos de cinco pies (pentámetro yámbico)
  31. ^ "BASTA | significado en el Diccionario Cambridge inglés". dictionary.cambridge.org . Consultado el 2020-08-02 . las cinco líneas y cuatro espacios entre ellas en las que se escriben las notas musicales
  32. ^ Ricker, Ramon (27 de noviembre de 1999). Escalas pentatónicas para improvisación en jazz. Alfred Music. pág. 2. ISBN 978-1-4574-9410-9Las escalas pentatónicas , como las que se utilizan en el jazz, son escalas de cinco notas.
  33. ^ Danneley, John Feltham (1825). Una enciclopedia o diccionario de música...: con más de doscientos ejemplos grabados, compilado en su totalidad a partir de las autoridades inglesas y extranjeras más célebres, intercalado con observaciones críticas y explicativas. editor y pub. son la cuarta perfecta, la quinta perfecta y la octava
  34. ^ Pelaia, Ariela. "Judaísmo 101: ¿Cuáles son los cinco libros de Moisés?". Aprende religiones . Consultado el 3 de agosto de 2020 .
  35. ^ Zenner, Walter P. (1 de enero de 1988). Persistencia y flexibilidad: perspectivas antropológicas sobre la experiencia judía estadounidense. SUNY Press. pág. 284. ISBN 978-0-88706-748-8.
  36. ^ "ENCICLOPEDIA CATÓLICA: Las cinco llagas sagradas". www.newadvent.org . Consultado el 2 de agosto de 2020 .
  37. ^ "PBS – Islam: Empire of Faith – Faith – Five Pillars" (El Islam: el imperio de la fe – La fe – Los cinco pilares) www.pbs.org . Consultado el 3 de agosto de 2020 .
  38. ^ Sarhangi, Reza (2012). "Polígonos estelares entrelazados en la arquitectura persa: el caso especial del decagrama en diseños de mosaicos" (PDF) . Nexus Network Journal . 14 (2): 350. doi : 10.1007/s00004-012-0117-5 . S2CID  124558613.
  39. ^ Yoon, Hong-key (2006). La cultura del feng shui en Corea: una exploración de la geomancia del este de Asia. Lexington Books. pág. 59. ISBN 978-0-7391-1348-6La primera categoría son los Cinco Agentes [Elementos], a saber: Agua, Fuego, Madera, Metal y Tierra.
  40. ^ Walsh, Len (15 de noviembre de 2008). Leer japonés hoy: la manera fácil de aprender 400 kanji prácticos. Tuttle Publishing. ISBN 978-1-4629-1592-7Los nombres japoneses de los días de la semana se toman de los nombres de los siete símbolos básicos de la naturaleza .
  41. ^ Chen, Yuan (2014). "Discurso de legitimación y teoría de los cinco elementos en la China imperial". Revista de estudios Song-Yuan . 44 (1): 325–364. doi :10.1353/sys.2014.0000. ISSN  2154-6665. S2CID  147099574.
  42. ^ Kronland-Martinet, Richard; Ystad, Solvi; Jensen, Kristoffer (19 de julio de 2008). Modelado y recuperación de música por computadora. Sense of Sounds: 4th International Symposium, CMMR 2007, Copenhague, Dinamarca, agosto de 2007, artículos revisados. Saltador. pag. 502.ISBN​ 978-3-540-85035-9Platón y Aristóteles postularon un quinto estado de la materia, al que llamaron "idea" o "quintaesencia" (de "quint" que significa "quinto").
  43. ^ «Anillos Olímpicos – Símbolo del Movimiento Olímpico». Comité Olímpico Internacional . 2020-06-23 . Consultado el 2020-08-02 .
  44. ^ Laplante, Philip A. (3 de octubre de 2018). Diccionario completo de ingeniería eléctrica. CRC Press. pág. 562. ISBN 978-1-4200-3780-7. quincunce de cinco puntos

Referencias

Lectura adicional

  • Curiosidades principales: 5
  • Medios relacionados con 5 (número) en Wikimedia Commons
Obtenido de "https://es.wikipedia.org/w/index.php?title=5&oldid=1251902452"