Pentagrama

Un pentagrama (a veces conocido como pentalfa, pentágono o pentágono estrella) es un polígono regular de cinco puntas , formado a partir de los segmentos de línea diagonales de un pentágono regular convexo (o simple, o que no se interseca consigo mismo) . Dibujar un círculo alrededor de las cinco puntas crea un símbolo similar conocido como pentáculo , [1] que es ampliamente utilizado por los wiccanos y en el paganismo , o como un signo de vida y conexiones.
La palabra pentagrama proviene del griego πεντάγραμμον ( pentagrammon ), [2] de πέντε ( pente ), "cinco" + γραμμή ( grammē ), "línea". [3] La palabra pentagrama se refiere solo a la estrella y la palabra pentáculo se refiere a la estrella dentro de un círculo, aunque hay cierta superposición en el uso. [4] La palabra pentalpha es un renacimiento del siglo XVII de un nombre griego posclásico de la forma. [5]
Historia
Historia temprana
Se han encontrado pentagramas tempranos en cerámica sumeria de Ur alrededor del 3500 a. C. , y la estrella de cinco puntas fue en varias ocasiones el símbolo de Ishtar o Marduk . [6] [7]


Se encontraron símbolos de pentagrama de hace unos 5.000 años en la cultura Liangzhu de China . [9]
El pentagrama era conocido por los antiguos griegos , con una representación en un jarrón que posiblemente data del siglo VII a. C. [10] El pitagorismo se originó en el siglo VI a. C. y utilizó el pentagrama como símbolo de reconocimiento mutuo, de bienestar y para reconocer las buenas acciones y la caridad. [11]
Entre los años 300 y 150 a. C. aproximadamente, el pentagrama fue el símbolo de Jerusalén, marcado por las cinco letras hebreas ירשלם que deletreaban su nombre. [12]
En el neoplatonismo , se decía que el pentagrama había sido utilizado como símbolo o signo de reconocimiento por los pitagóricos , quienes llamaban al pentagrama ὑγιεία hugieia "salud" [13].
Simbolismo occidental
Edad media
El pentagrama se utilizó en la antigüedad como símbolo cristiano de los cinco sentidos , [14] o de las cinco llagas de Cristo . El pentagrama juega un papel simbólico importante en el poema inglés del siglo XIV Sir Gawain and the Green Knight , en el que el símbolo decora el escudo del héroe, Gawain . El poeta anónimo atribuye el origen del símbolo al rey Salomón , y explica que cada uno de los cinco puntos interconectados representa una virtud ligada a un grupo de cinco: Gawain es perfecto en sus cinco sentidos y cinco dedos, fiel a las Cinco Llagas de Cristo, toma coraje de las cinco alegrías que María tuvo de Jesús, y ejemplifica las cinco virtudes de la caballería , [15] que son la generosidad, la amistad, la castidad, la caballerosidad y la piedad. [16]

El rosetón norte de la catedral de Amiens (construida en el siglo XIII) presenta un motivo basado en un pentagrama. Algunas fuentes interpretan que la inusual estrella que apunta hacia abajo simboliza el descenso del Espíritu Santo sobre las personas.
Renacimiento
Heinrich Cornelius Agrippa y otros perpetuaron la popularidad del pentagrama como símbolo mágico, atribuyendo los cinco elementos neoplatónicos a las cinco puntas, al estilo típico del renacimiento.
Romanticismo
A mediados del siglo XIX, entre los ocultistas se había desarrollado una distinción adicional en relación con la orientación del pentagrama. Con una sola punta hacia arriba, representaba al espíritu que presidía los cuatro elementos de la materia y era esencialmente "bueno". Sin embargo, el influyente pero controvertido escritor Éliphas Lévi , conocido por creer que la magia era una ciencia real, la había calificado de malvada cada vez que el símbolo aparecía al revés:
- “Un pentagrama invertido, con dos puntas proyectadas hacia arriba, es un símbolo del mal y atrae fuerzas siniestras porque trastorna el orden correcto de las cosas y demuestra el triunfo de la materia sobre el espíritu. Es el macho cabrío de la lujuria que ataca los cielos con sus cuernos, un signo aborrecido por los iniciados.” [17]
- “La estrella llameante, que, cuando se le da la vuelta, es el signo jeroglífico [ sic ] del macho cabrío de la magia negra , cuya cabeza puede estar dibujada en la estrella, los dos cuernos en la parte superior, las orejas a la derecha y a la izquierda, la barba en la parte inferior. Es un signo de antagonismo y fatalidad. Es el macho cabrío de la lujuria atacando los cielos con sus cuernos.” [18]
- “Mantengamos siempre en posición vertical la figura de la Estrella de Cinco Puntas, con el triángulo superior apuntando al cielo, pues es la sede de la sabiduría, y si la figura está invertida, el resultado será la perversión y el mal.” [19]
- Hombre inscrito en un pentagrama, de De occulta philosophia libri tres de Heinrich Cornelius Agrippa . Los cinco signos en los vértices del pentagrama son astrológicos .
- Otro pentagrama del libro de Agripa. Este tiene las letras pitagóricas inscritas alrededor del círculo.
- El pentagrama del ocultista y mago Éliphas Lévi , que él consideraba un símbolo del microcosmos o ser humano.
| Polígonos estelares |
|---|
El uso apotropaico (protector) en el folclore alemán del símbolo del pentagrama (llamado Drudenfuss en alemán) es mencionado por Goethe en Fausto (1808), donde un pentagrama impide a Mefistófeles salir de una habitación (pero no le impide entrar por el mismo camino, ya que la esquina que apunta hacia afuera del diagrama estaba dibujada de manera imperfecta):
Mefistófeles:
- Debo confesar que me lo impiden.
- Por una pequeña cosa que me estorba,
- El pie del druida en el umbral de tu puerta.
Fausto:
- ¿El Pentagrama te produce dolor?
- Entonces dime, Hijo del Infierno,
- Si ese es el caso, ¿cómo lo conseguiste?
- ¿Entrada? ¿Los espíritus como tú son engañados?
Mefistófeles:
- ¡Mira con atención! No está terminado:
- Un ángulo, si lo inspeccionas de cerca
- Como veis, ha quedado un poco abierto. [20]
También tiene carácter protector el uso en el folclore islandés de un pentagrama gestual o tallado en lugar de pintado (llamado smèrhnút en islandés), según el folclorista del siglo XIX Jón Árnason : [21]
- La mantequilla que sale del vómito falso se llama mantequilla falsa; parece otra cosa; pero si uno hace un signo de cruz sobre ella, o graba una cruz sobre ella, o una figura llamada nudo de suero de leche, * todo explota en pequeños pedazos y se convierte en un grano de escoria, de modo que no queda nada de ella, excepto partículas, o se hunde como espuma. Por lo tanto, parece más prudente, si a una persona se le ofrece una mantequilla horrible para comer, o como pago, [22] hacer una de las dos marcas sobre ella, porque una mantequilla falsa no puede soportar ni una marca de cruz ni un nudo de mantequilla.
- * El nudo de mantequilla tiene la siguiente forma:

Usos en el ocultismo moderno
Basado en el ocultismo de la era del Renacimiento, el pentagrama encontró su camino en el simbolismo de los ocultistas modernos. Su uso principal es una continuación del uso babilónico antiguo del pentagrama como un amuleto apotropaico para protegerse contra las fuerzas del mal. [23] Éliphas Lévi afirmó que "El pentagrama expresa el dominio de la mente sobre los elementos y es por este signo que atamos a los demonios del aire, los espíritus del fuego, los espectros del agua y los fantasmas de la tierra". [24] En este espíritu, la Orden Hermética de la Aurora Dorada desarrolló el uso del pentagrama en el ritual de destierro menor del pentagrama , que todavía se usa hasta el día de hoy por aquellos que practican la magia del tipo de la Aurora Dorada.
Aleister Crowley hizo uso del pentagrama en el sistema de magia utilizado en Thelema : un pentagrama adverso o invertido representa el descenso del espíritu a la materia, según la interpretación de Lon Milo DuQuette . [25] Crowley contradijo a sus antiguos camaradas de la Orden Hermética de la Aurora Dorada , quienes, siguiendo a Levi, consideraban esta orientación del símbolo como malvada y la asociaban con el triunfo de la materia sobre el espíritu.
Uso en nuevos movimientos religiosos
Fe Bahá'í

La estrella de cinco puntas es un símbolo de la Fe Bahá'í . [26] [27] En la Fe Bahá'í, la estrella es conocida como Haykal ( árabe : "templo" ), y fue iniciada y establecida por el Báb . El Báb y Bahá'u'lláh escribieron varias obras en forma de pentagrama. [28] [29]
La Iglesia de Jesucristo de los Santos de los Últimos Días
Se cree que la Iglesia de Jesucristo de los Santos de los Últimos Días comenzó a usar estrellas de cinco puntas tanto verticales como invertidas en la arquitectura del Templo , a partir del Templo de Nauvoo, Illinois, que se dedicó el 30 de abril de 1846. [30] Otros templos decorados con estrellas de cinco puntas en ambas orientaciones incluyen el Templo de Salt Lake y el Templo de Logan, Utah . Estos usos provienen del simbolismo que se encuentra en el capítulo 12 de Apocalipsis : "Y apareció una gran señal en el cielo: una mujer vestida del sol, con la luna debajo de sus pies, y sobre su cabeza una corona de doce estrellas". [31]
Wicca
Debido a una asociación percibida con el satanismo y el ocultismo, muchas escuelas de los Estados Unidos a fines de la década de 1990 buscaron evitar que los estudiantes exhibieran el pentagrama en la ropa o las joyas. [32] En las escuelas públicas, se determinó en 2000 que tales acciones por parte de los administradores violaban el derecho de los estudiantes a ejercer libremente su religión según la Primera Enmienda . [33]
El pentagrama rodeado por un círculo ( al que los demandantes se refieren como pentáculo ) fue añadido a la lista de 38 símbolos religiosos aprobados para ser colocados en las lápidas de los militares caídos en el Cementerio Nacional de Arlington el 24 de abril de 2007. La decisión se tomó tras diez solicitudes de familias de soldados caídos que practicaban la Wicca . El gobierno pagó a las familias 225.000 dólares estadounidenses para resolver sus demandas pendientes. [34] [35]
Otro uso religioso
satanismo
El pentagrama invertido se usa ampliamente en el satanismo , a veces representado con la cabeza de cabra de Baphomet , como lo popularizó la Iglesia de Satán desde 1968. Los satanistas de LaVey combinan la cabeza de cabra con letras hebreas en las cinco puntas del pentagrama para formar el Sigilo de Baphomet . El sigilo de Baphomet fue adaptado para el logotipo de Joy of Satan Ministries , usando caracteres cuneiformes en las cinco puntas del pentagrama, lo que refleja el uso más temprano de la forma en Sumeria . El pentagrama invertido también aparece en el logotipo de The Satanic Temple , con una representación alternativa de la cabeza de Baphomet. Otras representaciones de la cabeza de cabra satánica se parecen al pentagrama invertido sin su contorno explícito.
Religión de Serer
La estrella de cinco puntas es un símbolo de la religión serer y del pueblo serer de África occidental. Llamada Yoonir en su idioma , simboliza el universo en el mito de la creación serer y también representa a la estrella Sirio . [36] [37]
Otros usos modernos
- El pentagrama aparece en las banderas nacionales de Marruecos (adoptada en 1915) y Etiopía (adoptada en 1996 y readoptada en 2009).
- La Orden de la Estrella del Este , una organización (establecida en 1850) asociada con la masonería , utiliza un pentagrama como símbolo, con los cinco triángulos isósceles de las puntas coloreadas de azul, amarillo, blanco, verde y rojo. En la mayoría de los Grandes Capítulos, el pentagrama se utiliza apuntando hacia abajo, pero en unos pocos, apunta hacia arriba. Los oficiales de los Grandes Capítulos a menudo tienen un pentágono inscrito alrededor de la estrella [38] (el emblema que se muestra aquí es de la Asociación Prince Hall).
- Un pentagrama aparece en la bandera de la ciudad holandesa de Haaksbergen , así como en su escudo de armas.
- Bandera de Haaksbergen
- Un pentagrama aparece en la bandera de la ciudad japonesa de Nagasaki , así como en su emblema.
- Bandera de Nagasaki
Geometría

El pentagrama es el polígono regular estrellado más simple . El pentagrama contiene diez puntas (las cinco puntas de la estrella y los cinco vértices del pentágono interior) y quince segmentos de línea. Se representa con el símbolo de Schläfli {5/2}. Al igual que un pentágono regular y un pentágono regular con un pentagrama construido en su interior, el pentagrama regular tiene como grupo de simetría el grupo diedro de orden 10.
Puede verse como una red de una pirámide pentagonal aunque con triángulos isósceles.
Construcción
El pentagrama se puede construir conectando vértices alternos de un pentágono ; ver detalles de la construcción . También se puede construir como una estelación de un pentágono, extendiendo los bordes de un pentágono hasta que las líneas se intersequen.
Proporción áurea

La proporción áurea , φ = (1 + √ 5 ) / 2 ≈ 1,618, satisface:
juega un papel importante en los pentágonos y pentagramas regulares. Cada intersección de aristas secciona las aristas en la proporción áurea: la relación entre la longitud de la arista y el segmento más largo es φ , al igual que la longitud del segmento más largo y el más corto. Además, la relación entre la longitud del segmento más corto y el segmento delimitado por las dos aristas que se cruzan (un lado del pentágono en el centro del pentagrama) es φ . Como muestra la ilustración a cuatro colores:
El pentagrama incluye diez triángulos isósceles : cinco triángulos acutángulos y cinco obtusángulos . En todos ellos, la razón entre el lado más largo y el lado más corto es φ . Los triángulos acutángulos son triángulos áureos . El triángulo obtusángulo resaltado mediante líneas de colores en la ilustración es un gnomon áureo .
Valores trigonométricos
En consecuencia, en un triángulo isósceles con uno o dos ángulos de 36°, el lado más largo de los dos es φ veces el más corto de los dos, tanto en el caso del triángulo agudo como en el caso del obtuso.
Pentagrama esférico
Un pentagrama puede dibujarse como un polígono estrellado sobre una esfera, compuesto por cinco arcos de círculo máximo, cuyos ángulos internos son todos rectos. Esta forma fue descrita por John Napier en su libro de 1614 Mirifici logarithmorum canonis descriptio (Descripción de la maravillosa regla de los logaritmos) junto con reglas que vinculan los valores de las funciones trigonométricas de cinco partes de un triángulo esférico rectángulo (dos ángulos y tres lados). Fue estudiada más tarde por Carl Friedrich Gauss .
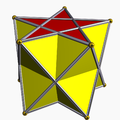
Figuras tridimensionales
Varios poliedros incorporan pentagramas:
Dimensiones superiores
Las proyecciones ortogonales de politopos de dimensiones superiores también pueden crear figuras pentagrámicas:
| 4D | 5D | ||
|---|---|---|---|
 El triángulo regular de 5 celdas (4- símplex ) tiene cinco vértices y 10 aristas. |  La celda rectificada de 5 tiene 10 vértices y 30 aristas. |  El 5-símplex rectificado tiene 15 vértices, vistos en esta proyección ortogonal como tres pentagramas anidados. |  El 5-símplex birectificado tiene 20 vértices, vistos en esta proyección ortogonal como cuatro pentagramas superpuestos. |
Los diez 4- politopos de Schläfli–Hess de cuatro dimensiones tienen caras pentagramáticas o elementos de figura de vértice .
Pentagrama de Venus

El pentagrama de Venus es la trayectoria aparente del planeta Venus tal como se observa desde la Tierra . Las conjunciones inferiores sucesivas de Venus se repiten con una resonancia orbital de aproximadamente 13:8, es decir, Venus orbita alrededor del Sol aproximadamente 13 veces por cada ocho órbitas de la Tierra, desplazándose 144° en cada conjunción inferior. [40] Las puntas de los cinco bucles en el centro de la figura tienen la misma relación geométrica entre sí que los cinco vértices , o puntos, de un pentagrama, y cada grupo de cinco intersecciones equidistantes del centro de la figura tienen la misma relación geométrica.
En sistemas informáticos
El pentagrama tiene estos puntos de código Unicode que permiten incluirlo en documentos:
- U+26E4 ⛤ PENTAGRAMA
- U+26E5 ⛥ PENTAGRAMA ENTRELAZADO PARA DIESTRO
- U+26E6 ⛦ PENTAGRAMA ENTRELAZADO PARA IZQUIERDOS
- U+26E7 ⛧ PENTAGRAMA INVERTIDO
Véase también
- Abe no Seimei – Místico japonés
- Simbolismo cristiano : uso de símbolos, incluidos arquetipos, actos, obras de arte o eventos, por parte del cristianismo.
- Insignia del Mando en el Mar : insignia en el ejército de los EE. UU.
- Eneagrama (geometría) : Polígono de estrella de nueve puntas
- Estrella de cinco puntas : ideograma común en la cultura moderna
- Heptagrama – Polígono estrellado de 7 lados
- Hexagrama – Polígono de estrella de seis puntas
- Laúd de Pitágoras – Figura geométrica autosimilar
- Medalla de Honor : el galardón más alto de las Fuerzas Armadas de los Estados Unidos
- Pentachoron – el 4- símplex
- Mapa de pentagramas : sistema dinámico discreto en el espacio de módulos de polígonos en el plano proyectivo
- Pentalpha – Rompecabezas con piedras y un pentagrama
- Gráfico de Petersen : gráfico cúbico con 10 vértices y 15 aristas
- Teorema de Ptolomeo : Relaciona los 4 lados y 2 diagonales de un cuadrilátero con vértices en un círculo común.
- Sello de Salomón – Anillo de sello atribuido al rey israelita Salomón
- Polígonos estelares en el arte y la cultura – Los polígonos como elementos simbólicos
- Estrella (heráldica) – Símbolo heráldico
- Polígonos estrellados : extensión de los elementos de un politopo para formar una nueva figura
Referencias
- ^ Gene Brown (nd). "Diferencia entre pentagrama y pentáculo". Diferencia entre . Consultado el 29 de junio de 2023 .
- ^ πεντάγραμμον, Henry George Liddell, Robert Scott, Un léxico griego-inglés , sobre Perseo; una forma sustantiva de adjetivo πεντάγραμμος ( pentagrammos ) o πεντέγραμμος ( pentegrammos ), una palabra que significa aproximadamente "cinco líneas" o "cinco líneas"
- ^ πέντε, Henry George Liddell, Robert Scott, A Greek-English Lexicon , sobre Perseo; Satanás, los tres nombres mencionados antes del amanecer γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon , sobre Perseo
- ^ este uso está confirmado por el Oxford English Dictionary, aunque esa obra especifica que una circunscripción tiene la forma de una estrella de cinco puntas y su étimo, el latín posclásico pentaculum [...] Un pentagrama, especialmente uno encerrado en un círculo; un talismán o símbolo mágico en forma de pentagrama o inscrito con un pentagrama. También, en uso extendido: cualquier símbolo mágico similar (frecuentemente aplicado a un hexagrama formado por dos triángulos equiláteros que se cruzan o entrelazan).
- ^ πένταλφα, "cinco Alfas", interpretando la forma como cinco formas Α superpuestas en ángulos de 72 grados.
- ^ Budge, Sir EA Wallis (1968). Amuletos y talismanes . pág. 433.
- ^ Scott, Dustin Jon (2006). «Historia del pentagrama» . Consultado el 18 de mayo de 2021 .
- ^ Allman, GJ, Geometría griega desde Tales hasta Euclides (1889), p.26.
- ^ 馬愛平 (23 de septiembre de 2019). "距今5000年!良渚文物中發現最古老五角星圖案" (en chino). Diario de China.
- ^ Coxeter, HSM; Politopos regulares , 3.ª ed., Dover, 1973, pág. 114.
- ^ Ball, WW Rouse y Coxeter, HSM; Recreaciones y ensayos matemáticos , 13.ª edición, Dover, 1987, pág. 176.
- ^ "Estrella de David vs. Pentagrama: Todo lo que necesitas saber". 17 de julio de 2020.
- ^ Allman, GJ, Greek Geometry From Thales to Euclid , parte I (1877), en Hermathena 3.5, pp. 183, 197, citando a Jámblico y al Escoliasta sobre Aristófanes. Se dice que el pentagrama recibió ese nombre porque el propio Pitágoras escribió las letras Υ, Γ, Ι, Θ (= /ei/), Α en sus vértices.
- ^ Símbolos cristianos antiguos y modernos , Child, Heather y Dorothy Colles. Nueva York: Charles Scribner's Sons, 1971, ISBN 0-7135-1960-6 .
- ^ Morgan, Gerald (1979). "El significado del simbolismo del pentágono en 'Sir Gawain y el caballero verde'"". The Modern Language Review . 74 (4): 769–790. doi :10.2307/3728227. JSTOR 3728227.
- ^ Sir Gawain y el Caballero Verde , líneas 619–665
- ^ Lévi, Éliphas (1999) [1896 (traducido), 1854 (publicado por primera vez)]. Magia trascendental, su doctrina y ritual [ Dogme et rituel de la haute magie ]. Trans. por AE Waite . Playa de York : Weiser . OCLC 263626874.
- ^ Lévi, Éliphas (2002) [1939 (traducido), 1859 (publicado por primera vez)]. La Clave de los Misterios [ la Clef des grands mystères suivant Hénoch, Abraham, Hermès Trismégiste et Salomon ]. Trans. por Aleister Crowley . Boston: Weiser . pag. 69. OCLC 49053462.
- ^ Hartmann, Franz (1895) [1886]. Magia, blanca y negra (5.ª ed.). Nueva York: The Path. OCLC 476635673.
- ^ "Goethe, Johann Wolfgang von (1749–1832) - Fausto, Parte I: Escenas I a III". www.poetryintranslation.com . Consultado el 25 de mayo de 2021 .
- ^ Árnason, Jón (1862). " Töfrabrogð [truco de magia]". Íslenzkar Þjoðsögur og Æfintýri [Cuentos populares y leyendas islandeses ] (en islandés). vol. 1. Leipzig : Librería de JC Hinrich. pag. 432.
Smèr það, er verður af tilberaspýunni, er kallað tilberasmèr; er það útlits sem annað smèr; en gjöri maður krossmark yfir því, eða risti á það kross, eða mynd þá, er smèrhnútur heitir,
*
springur það alt í smámola og verður eins og draflakyrníngur, svo ekki sèst eptir af því, agnir einar, eða það hjaðnar niður sem froða . Þykir það því varlegra, ef manni er boðið óhrjálegt smèr að borða, eða í gjöld, að gjóra annaðhvort þetta mark á það, því tilberasmèr þolir hvorki krossmark né hnút. / * Smèrhnútur er svo í lögun:

- ^ En la Edad Media, la mantequilla se utilizaba como forma de pago, por ejemplo, el alquiler. Véase:
• Sexton, Regina (2003). "El papel y la función de la mantequilla en la dieta del monje y el penitente en la Irlanda medieval temprana". En Walker, Harlan (ed.). La grasa de la tierra: Actas del Simposio de Oxford sobre comida y cocina de 2002. Bristol: Footwork. págs. 253-269. - ^ Schouten, enero (1968). El pentagrama como símbolo médico: un estudio iconológico. Hes y De Graaf. pag. 18.ISBN 978-90-6004-166-6.
- ^ Waite, Arthur Edward (1886). Los misterios de la magia: un compendio de los escritos de Eliphas Lévi. Londres: George Redway. pág. 136.
- ^ DuQuette, Lon Milo (2003). La magia de Aleister Crowley: un manual de los rituales de Thelema. Weiser Books. págs. 93, 247. ISBN 978-1-57863-299-2.
- ^ "Biblioteca de Referencia Bahá'í - Directivas del Guardián, páginas 51-52". reference.bahai.org .
- ^ "La estrella de nueve puntas". bahai-library.com .
- ^ Moojan Momen (2019). La Tabla Estelar del Bab. Blog de la Biblioteca Británica.
- ^ Bayat, Mohamad Ghasem (2001). Introducción al Súratu'l-Haykal (Discurso del Templo) en Luces de Irfan, Libro 2.
- ^ Véase el sitio web del Templo de Nauvoo, archivado el 17 de mayo de 2020 en Wayback Machine, donde se analiza su arquitectura y, en particular, la página sobre el simbolismo exterior del Templo de Nauvoo, archivado el 17 de mayo de 2020 en Wayback Machine . Consultado el 16 de diciembre de 2006.
- ^ Brown, Matthew B (2002). "Estrellas invertidas en los templos mormones" (PDF) . FAIRLDS.org . Archivado desde el original (PDF) el 29 de febrero de 2008.
- ^ "Religious Apparel in School", Robinson, BA, Ontario Consultants on Religious Tolerance, 20 de agosto de 1999, actualizado el 29 de abril de 2005. Consultado el 10 de febrero de 2006. "ACLU Defends Honor Student Witch Pentacle" (Comunicado de prensa). Unión Estadounidense por las Libertades Civiles de Michigan. 10 de febrero de 1999. Archivado desde el original el 8 de noviembre de 2003. Consultado el 10 de febrero de 2006 .
{{cite press release}}: CS1 maint: bot: original URL status unknown (link)"Brujas y guardarropas: un niño dice que lo suspendieron de la escuela por llevar un símbolo mágico" Rouvalis, Cristina; Pittsburgh Post-Gazette, 27 de septiembre de 2000. Consultado el 10 de febrero de 2006. - ^ "Juez federal defiende el derecho de los estudiantes de Indiana a llevar símbolos wiccanos". Associated Press. 1 de mayo de 2000. Archivado desde el original el 30 de marzo de 2014. Consultado el 21 de septiembre de 2007 .
- ^ "El símbolo wiccan es aceptable para las tumbas de los soldados". CNN.com . Associated Press. 23 de abril de 2007. Archivado desde el original el 26 de abril de 2007.
- ^ "Entierros y monumentos conmemorativos: emblemas de creencias disponibles para su colocación en lápidas y marcadores gubernamentales". Departamento de Asuntos de Veteranos de los Estados Unidos . 3 de julio de 2013 . Consultado el 13 de enero de 2014 .
- ^ Gravrand, Henry (1990). La civilización Sereer, Volumen II: Pangool . Nouvelles éditions Africaines du Sénégal (en francés). Dakar, Senegal. pag. 20.ISBN 2-7236-1055-1.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Madiya, Clémentine Faïk-Nzuji (1996). Rastreando la memoria: un glosario de signos y símbolos gráficos en el arte y la cultura africanos . Serie Mercury, n.º 71. Hull, Québec: Museo Canadiense de la Civilización. pp. 27, 155. ISBN 0-660-15965-1.
- ^ Ritual de la Orden de la Estrella del Este, 1976
- ^ Pietrocola, Giorgio (2005). "Tartapelago. Exposición de fractales". Maecla .
- ^ Baez, John (4 de enero de 2014). «El pentagrama de Venus». Azimuth . Archivado desde el original el 14 de diciembre de 2015 . Consultado el 7 de enero de 2016 .
Lectura adicional
- Becker, Udo (1994). "Pentagrama". La enciclopedia de símbolos del continuo . Traducido por Garmer, Lance W. Nueva York: Continuum Books. pp. 230ff. ISBN 978-0-8264-0644-6.
- Conway, John Horton ; Burgiel, Heidi; Goodman-Strauss, Chaim (abril de 2008). "Capítulo 26, Más alto aún: politopos estelares regulares". Las simetrías de las cosas . Wellesley, Massachusetts: AK Peters. pág. 404. ISBN 978-1-56881-220-5.
- Ferguson, George Wells (1966) [1954]. Signos y símbolos en el arte cristiano . Nueva York: Oxford University Press. pág. 59. OCLC 65081051.
- Grünbaum, Branko ; Shephard, Geoffrey Colin (1987). Mosaicos y patrones. Nueva York: WH Freeman. ISBN 978-0-7167-1193-3.
- Grünbaum, Branko (1994). "Poliedros con caras huecas". En Bisztriczky, T.; McMullen, P .; Schneider, A.; Weiss, A. Ivić (eds.). Politopos: abstractos, convexos y computacionales . NATO ASI Series C: Ciencias matemáticas y físicas. Vol. 440. Dordrecht: Springer Netherlands. págs. 43–70. doi :10.1007/978-94-011-0924-6_3. ISBN . 978-94-010-4398-4.
Enlaces externos
- Weisstein, Eric W. "Pentagrama". MathWorld .
- El Pentáculo Pitagórico de la Biblioteca Arcana.
.jpg/440px-Pentagram_and_human_body_(Agrippa).jpg)

.jpg/440px-Pentagram_(Levi).jpg)










![{\displaystyle {\begin{aligned}\sin {\frac {\pi }{10}}&=\sin 18^{\circ }={\frac {{\sqrt {5}}-1}{4}}={\frac {\varphi -1}{2}}={\frac {1}{2\varphi }}\\[5pt]\cos {\frac {\pi }{10}}&=\cos 18^{\circ }={\frac {\sqrt {2(5+{\sqrt {5}})}}{4}}\\[5pt]\tan {\frac {\pi }{10}}&=\tan 18^{\circ }={\frac {\sqrt {5(5-2{\sqrt {5}})}}{5}}\\[5pt]\cot {\frac {\pi }{10}}&=\cot 18^{\circ }={\sqrt {5+2{\sqrt {5}}}}\\[5pt]\sin {\frac {\pi }{5}}&=\sin 36^{\circ }={\frac {\sqrt {2(5-{\sqrt {5}})}}{4}}\\[5pt]\cos {\frac {\pi }{5}}&=\cos 36^{\circ }={\frac {{\sqrt {5}}+1}{4}}={\frac {\varphi }{2}}\\[5pt]\tan {\frac {\pi }{5}}&=\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}\\[5pt]\cot {\frac {\pi }{5}}&=\cot 36^{\circ }={\frac {\sqrt {5(5+2{\sqrt {5}})}}{5}}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/617d763508332673e70ff432476f3b0988117be7)