5-símplex estericados
  5-símplex          |   Estericado 5-símplex          | ||
  Esteritruncado 5-símplex          |   Estericantelado 5-símplex          | ||
  Estericantitruncado 5-símplex          |   Esteriruncitruncado 5-simplex          | ||
  Esteriruncicantitruncado 5-simplex (Omnitruncado 5-simplex)          | |||
| Proyecciones ortogonales en los planos de Coxeter A 5 y A 4 | |||
|---|---|---|---|
En geometría de cinco dimensiones , un 5-símplex estericizado es un 5-politopo uniforme convexo con truncamientos de cuarto orden ( estericación ) del 5-símplex regular .
Existen seis estericaciones únicas del 5-símplex, incluidas permutaciones de truncamientos, cantelaciones y runcinaciones. El 5-símplex esterificado más simple también se denomina 5-símplex expandido , con el primer y el último nodo en forma de anillo, por ser construible mediante una operación de expansión aplicada al 5-símplex regular. La forma más alta, el 5-símplex esterificado antitruncado, se denomina de manera más sencilla 5-símplex omnitruncado con todos los nodos en forma de anillo.
Estericado 5-símplex
| Estericado 5-símplex | ||
| Tipo | Politopo 5 uniforme | |
| Símbolo de Schläfli | 2r2r{3,3,3,3} 2r{3 2,2 } = | |
| Diagrama de Coxeter-Dynkin |          o      | |
| 4 caras | 62 | 6+6 {3,3,3} 15+15 {}×{3,3}  20 {3}×{3}  |
| Células | 180 | 60 {3,3} 120 {}×{3}  |
| Caras | 210 | 120 {3} 90 {4} |
| Bordes | 120 | |
| Vértices | 30 | |
| Figura de vértice |  Antiprisma tetraédrico | |
| Grupo Coxeter | A 5 × 2, [[3,3,3,3]], orden 1440 | |
| Propiedades | convexo , isogonal , isotoxal | |
Un 5-símplex estericable se puede construir mediante una operación de expansión aplicada al 5-símplex regular , y por lo tanto también se lo denomina a veces 5-símplex expandido . Tiene 30 vértices , 120 aristas , 210 caras (120 triángulos y 90 cuadrados ), 180 celdas (60 tetraedros y 120 prismas triangulares ) y 62 4-caras (12 5-celdas , 30 prismas tetraédricos y 20 duoprismas 3-3 ).
Nombres alternativos
- 5-símplex expandido
- Hexateron estericado
- Dodecaterón celulado pequeño (acrónimo: scad) (Jonathan Bowers) [1]
Secciones transversales
La sección transversal máxima del hexaterón esterificado con un hiperplano de 4 dimensiones es una 5-celda runcinada . Esta sección transversal divide el hexaterón esterificado en dos hipercúpulas pentacorales que constan de 6 5-celdas , 15 prismas tetraédricos y 10 duoprismas 3-3 cada una.
Coordenadas
Los vértices del 5-símplex estericizado se pueden construir en un hiperplano en el 6-espacio como permutaciones de (0,1,1,1,1,2). Esto representa la faceta ortante positiva del 6-ortoplex estericizado .
Una segunda construcción en el espacio 6, desde el centro de un ortoplex 6 rectificado, se da mediante permutaciones de coordenadas de:
- (1,-1,0,0,0,0)
Las coordenadas cartesianas en el espacio 5 para los vértices normalizados de un hexaterón estericulado centrado en el origen son:
Sistema de raíces
Sus 30 vértices representan los vectores raíz del grupo de Lie simple A 5 . También es la figura de vértice del panal 5-símplex .
Imágenes
| Un avión de Coxeter | Un 5 | Un 4 |
|---|---|---|
| Gráfico | 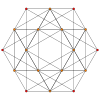 |  |
| Simetría diedral | [6] | [[5]]=[10] |
| Un avión de Coxeter | Un 3 | Un 2 |
| Gráfico |  |  |
| Simetría diedral | [4] | [[3]]=[6] |
 proyección ortogonal con simetría [6] |
Esteritruncado 5-símplex
| Esteritruncado 5-símplex | ||
| Tipo | Politopo 5 uniforme | |
| Símbolo de Schläfli | t0,1,4 { 3,3,3,3 } | |
| Diagrama de Coxeter-Dynkin |          | |
| 4 caras | 62 | 6 t{3,3,3} 15 {}× t{3,3} 20 {3}×{6} 15 {}× {3,3} 6 t 0,3 {3,3,3} |
| Células | 330 | |
| Caras | 570 | |
| Bordes | 420 | |
| Vértices | 120 | |
| Figura de vértice |  | |
| Grupo Coxeter | A 5 [3,3,3,3], orden 720 | |
| Propiedades | convexo , isogonal | |
Nombres alternativos
- Hexateron esteritruncado
- Hexateron celiprismado (acrónimo: cappix) (Jonathan Bowers) [2]
Coordenadas
Las coordenadas se pueden realizar en el espacio 6, como 180 permutaciones de:
- (0,1,1,1,2,3)
Esta construcción existe como una de las 64 facetas ortantes del 6-ortoplex esteritruncado .
Imágenes
| Un avión de Coxeter | Un 5 | Un 4 |
|---|---|---|
| Gráfico |  |  |
| Simetría diedral | [6] | [5] |
| Un avión de Coxeter | Un 3 | Un 2 |
| Gráfico |  |  |
| Simetría diedral | [4] | [3] |
Estericantelado 5-símplex
| Estericantelado 5-símplex | ||
| Tipo | Politopo 5 uniforme | |
| Símbolo de Schläfli | t0,2,4 { 3,3,3,3 } | |
| Diagrama de Coxeter-Dynkin |          o      | |
| 4 caras | 62 | 12 rr{3,3,3} 30 rr{3,3}x {} 20 {3}×{3} |
| Células | 420 | 60 r{3,3} 240 {}×{3} 90 {}×{}×{} 30 r{3,3} |
| Caras | 900 | 360 {3} 540 {4} |
| Bordes | 720 | |
| Vértices | 180 | |
| Figura de vértice |  | |
| Grupo Coxeter | A 5 × 2, [[3,3,3,3]], orden 1440 | |
| Propiedades | convexo , isogonal | |
Nombres alternativos
- Hexateron estericantelado
- Dodecateron celirrombado (Acrónimo: card) (Jonathan Bowers) [3]
Coordenadas
Las coordenadas se pueden realizar en el espacio de 6, como permutaciones de:
- (0,1,1,2,2,3)
Esta construcción existe como una de las 64 facetas ortantes del 6-ortoplex estericantelado .
Imágenes
| Un avión de Coxeter | Un 5 | Un 4 |
|---|---|---|
| Gráfico |  |  |
| Simetría diedral | [6] | [[5]]=[10] |
| Un avión de Coxeter | Un 3 | Un 2 |
| Gráfico |  |  |
| Simetría diedral | [4] | [[3]]=[6] |
Estericantitruncado 5-símplex
| Estericantitruncado 5-símplex | ||
| Tipo | Politopo 5 uniforme | |
| Símbolo de Schläfli | t0,1,2,4 { 3,3,3,3 } | |
| Diagrama de Coxeter-Dynkin |          | |
| 4 caras | 62 | |
| Células | 480 | |
| Caras | 1140 | |
| Bordes | 1080 | |
| Vértices | 360 | |
| Figura de vértice |  | |
| Grupo Coxeter | A 5 [3,3,3,3], orden 720 | |
| Propiedades | convexo , isogonal | |
Nombres alternativos
- Hexateron antitruncado esterico
- Hexateron hombatado de Cellicreator (acrónimo: cograx) (Jonathan Bowers) [4]
Coordenadas
Las coordenadas se pueden realizar en el espacio 6, como 360 permutaciones de:
- (0,1,1,2,3,4)
Esta construcción existe como una de las 64 facetas ortantes del 6-ortoplex estericoantitruncado .
Imágenes
| Un avión de Coxeter | Un 5 | Un 4 |
|---|---|---|
| Gráfico |  |  |
| Simetría diedral | [6] | [5] |
| Un avión de Coxeter | Un 3 | Un 2 |
| Gráfico |  |  |
| Simetría diedral | [4] | [3] |
Esteriruncitruncado 5-simplex
| Esteriruncitruncado 5-simplex | ||
| Tipo | Politopo 5 uniforme | |
| Símbolo de Schläfli | t0,1,3,4 { 3,3,3,3 } 2t{3 2,2 } | |
| Diagrama de Coxeter-Dynkin |          o      | |
| 4 caras | 62 | 12 t 0,1,3 {3,3,3} 30 {} × t{3,3} 20 {6} × {6} |
| Células | 450 | |
| Caras | 1110 | |
| Bordes | 1080 | |
| Vértices | 360 | |
| Figura de vértice |  | |
| Grupo Coxeter | A 5 × 2, [[3,3,3,3]], orden 1440 | |
| Propiedades | convexo , isogonal | |
Nombres alternativos
- Hexateron esteriruncitruncado
- Dodecaterón truncado de celiprisma (acrónimo: captid) (Jonathan Bowers) [5]
Coordenadas
Las coordenadas se pueden realizar en el espacio 6, como 360 permutaciones de:
- (0,1,2,2,3,4)
Esta construcción existe como una de las 64 facetas ortantes del 6-ortoplex esteriruncitruncado .
Imágenes
| Un avión de Coxeter | Un 5 | Un 4 |
|---|---|---|
| Gráfico |  |  |
| Simetría diedral | [6] | [[5]]=[10] |
| Un avión de Coxeter | Un 3 | Un 2 |
| Gráfico |  |  |
| Simetría diedral | [4] | [[3]]=[6] |
5-símplex omnitruncado
| 5-símplex omnitruncado | ||
| Tipo | Politopo 5 uniforme | |
| Símbolo de Schläfli | t 0,1,2,3,4 {3,3,3,3} 2tr{3 2,2 } | |
Diagrama de Coxeter-Dynkin |          o      | |
| 4 caras | 62 | 12 t0,1,2,3 { 3,3,3} 30 {}×tr{3,3}  20 {6}×{6}  |
| Células | 540 | 360 t{3,4} 90 {4,3}  90 {}×{6}  |
| Caras | 1560 | 480 {6} 1080 {4} |
| Bordes | 1800 | |
| Vértices | 720 | |
| Figura de vértice |  5 celdas irregulares | |
| Grupo Coxeter | A 5 × 2, [[3,3,3,3]], orden 1440 | |
| Propiedades | convexo , isogonal , zonotopo | |
El 5-símplex omnitruncado tiene 720 vértices , 1800 aristas , 1560 caras (480 hexágonos y 1080 cuadrados ), 540 celdas (360 octaedros truncados , 90 cubos y 90 prismas hexagonales ) y 62 4-caras (12 5-celdas omnitruncadas , 30 prismas octaédricos truncados y 20 duoprismas 6-6 ).
Nombres alternativos
- Steriruncicantitruncated 5-simplex (Descripción completa de omnitruncamiento para 5-politopos por Johnson)
- Hexaterón omnitruncado
- Gran dodecaterón celulado (acrónimo: gocad) (Jonathan Bowers) [6]
Coordenadas
Los vértices del 5-símplex omnitruncado se pueden construir de forma más sencilla en un hiperplano en el espacio 6 como permutaciones de (0,1,2,3,4,5). Estas coordenadas provienen de la faceta ortante positiva del 6-ortoplex esteriruncicantitruncado , t 0,1,2,3,4 {3 4 ,4},









 .
.
Imágenes
| Un avión de Coxeter | Un 5 | Un 4 |
|---|---|---|
| Gráfico |  |  |
| Simetría diedral | [6] | [[5]]=[10] |
| Un avión de Coxeter | Un 3 | Un 2 |
| Gráfico |  |  |
| Simetría diedral | [4] | [[3]]=[6] |

Permutoedro
El 5-símplex omnitruncado es el permutoedro de orden 6. También es un zonotopo , la suma de Minkowski de seis segmentos de línea paralelos a las seis líneas que pasan por el origen y los seis vértices del 5-símplex.
 Proyección ortogonal , vértices etiquetados como permutoedro . |
Panal relacionado
El panal omnitruncado 5-símplex está formado por facetas omnitruncadas 5-símplex con 3 facetas alrededor de cada cresta . Tiene un diagrama de Coxeter-Dynkin de



 .
.
| Grupo Coxeter | |||||
|---|---|---|---|---|---|
| Coxeter-Dynkin |    |    |    |      |      |
| Imagen |  |  |  | ||
| Nombre | Apeirogon | Hextil | Panal de abeja 3-símplex omnitruncado | Panal de abeja 4-símplex omnitruncado | Panal de abeja 5-símplex omnitruncado |
| Facetas |  |  |  |  |  |
Snub completo 5-simplex
El 5-simplex truncado completo u omnisnub 5-simplex , definido como una alternancia del 5-simplex omnitruncado, no es uniforme, pero se puede dar un diagrama de Coxeter.







 y simetría [[3,3,3,3]] + , y construido a partir de 12 celdas 5 romos , 30 antiprismas tetraédricos romos , 20 duoantiprismas 3-3 y 360 celdas 5 irregulares que llenan los huecos en los vértices eliminados.
y simetría [[3,3,3,3]] + , y construido a partir de 12 celdas 5 romos , 30 antiprismas tetraédricos romos , 20 duoantiprismas 3-3 y 360 celdas 5 irregulares que llenan los huecos en los vértices eliminados.
Politopos uniformes relacionados
Estos politopos son parte de 19 5-politopos uniformes basados en el grupo de Coxeter [3,3,3,3] , todos mostrados aquí en proyecciones ortográficas del plano de Coxeter A 5. (Los vértices están coloreados por orden de superposición de proyección, rojo, naranja, amarillo, verde, cian, azul, violeta tienen progresivamente más vértices)
| Politopos A5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 el 0 |  el 1 |  dos |  t0,1 |  t0,2 |  1,2 |  t0,3 | |||||
 1,3 |  0,4 |  0,1,2 |  t0,1,3 |  0,2,3 |  1,2,3 |  0,1,4 | |||||
 0,2,4 |  0,1,2,3 |  0,1,2,4 |  0,1,3,4 |  0,1,2,3,4 | |||||||
Notas
- ^ Klitizing, (x3o3o3o3x - scad)
- ^ Klitizando, (x3x3o3o3x-cappix)
- ^ Klitizing, (x3o3x3o3x - tarjeta)
- ^ Klitizando, (x3x3x3o3x - cograx)
- ^ Klitizing, (x3x3o3x3x - cáptido)
- ^ Klitizing, (x3x3x3x3x - gocad)
Referencias
- HSM Coxeter :
- HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
- (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
- Manuscrito de politopos uniformes de Norman Johnson (1991)
- NW Johnson: La teoría de politopos uniformes y panales , Ph.D.
- Klitzing, Richard. "Polítopos uniformes 5D (politera)".x3o3o3o3x - scad, x3x3o3o3x - cappix, x3o3x3o3x - tarjeta, x3x3x3o3x - cograx, x3x3o3x3x - captid, x3x3x3x3x - gocad
Enlaces externos
- Glosario del hiperespacio, George Olshevsky.
- Politopos de varias dimensiones
- Glosario multidimensional













