Cuboctaedro
Poliedro con 8 caras triangulares y 6 caras cuadradas
Cuboctaedro
TipoSólido arquimediano
Caras14
Bordes24
Vértices12
Configuración de vértice3.4.3.4
Grupo de simetríaSimetría octaédrica Simetría tetraédrica Oh yo {\displaystyle \mathrm {O} _ {\mathrm {h} }}
yo d {\displaystyle \mathrm {T} _ {\mathrm {d} }}
Angulo diedro ( grados )aproximadamente 125°
Poliedro dualDodecaedro rómbico
Propiedadesconvexo ,
equilibrio vectorial,
propiedad de Rupert
Figura de vértice
Neto

Un cuboctaedro es un poliedro con 8 caras triangulares y 6 caras cuadradas. Un cuboctaedro tiene 12 vértices idénticos , con 2 triángulos y 2 cuadrados que se encuentran en cada uno, y 24 aristas idénticas , cada una separando un triángulo de un cuadrado. Como tal, es un poliedro cuasirregular , es decir, un sólido arquimediano que no solo es transitivo por vértices sino también por aristas . [1] Es radialmente equilátero. Su poliedro dual es el dodecaedro rómbico .

Construcción

El cuboctaedro se puede construir de muchas maneras:

  • Su construcción puede iniciarse uniendo dos cúpulas triangulares regulares base con base. Esto es similar a uno de los sólidos de Johnson, la ortobicúpula triangular . La diferencia es que la ortobicúpula triangular se construye con una de las cúpulas torcida de modo que las caras poligonales similares sean adyacentes, mientras que el cuboctaedro no lo es. Como resultado, el cuboctaedro también puede llamarse girobicúpula triangular . [2]
  • Su construcción puede iniciarse a partir de un cubo o de un octaedro regular , marcando los puntos medios de sus aristas, y cortando todos los vértices en esos puntos. Este proceso se conoce como rectificación , por lo que al cuboctaedro se le denomina cubo rectificado y octaedro rectificado . [3]
  • Una construcción alternativa es mediante el corte de todos los vértices, conocido como truncamiento . Se puede partir de un tetraedro regular , cortando los vértices y biselando las aristas. Este proceso se conoce como cantelación , lo que hace que el cuboctaedro se denomine tetraedro cantelado . [4]

De todas estas construcciones, el cuboctaedro tiene 14 caras: 8 triángulos equiláteros y 6 cuadrados. También tiene 24 aristas y 12 vértices. [5]

Las coordenadas cartesianas para los vértices de un cuboctaedro con longitud de arista centrada en el origen son: [6] 2 {\displaystyle {\sqrt {2}}} ( ± 1 , ± 1 , 0 ) , ( ± 1 , 0 , ± 1 ) , ( 0 , ± 1 , ± 1 ) . {\displaystyle (\pm 1,\pm 1,0),\qquad (\pm 1,0,\pm 1),\qquad (0,\pm 1,\pm 1).}

Propiedades

Medición y otras propiedades métricas

El área de la superficie de un cuboctaedro se puede determinar sumando todas las áreas de sus caras poligonales. El volumen de un cuboctaedro se puede determinar dividiendo el cubo en dos cúpulas triangulares regulares y sumando sus volúmenes. Dado que la longitud de la arista , su área de superficie y volumen son: [5] A {\estilo de visualización A} V {\estilo de visualización V} a {\estilo de visualización a} A = ( 6 + 2 3 ) a 2 ≈ 9.464 a 2 V = 5 2 3 a 3 ≈ 2.357 a 3 . {\displaystyle {\begin{aligned}A&=\left(6+2{\sqrt {3}}\right)a^{2}&&\aproximadamente 9,464a^{2}\\V&={\frac {5{\sqrt {2}}}{3}}a^{3}&&\aproximadamente 2,357a^{3}.\end{aligned}}}

El ángulo diedro de un cuboctaedro se puede calcular con el ángulo de las cúpulas triangulares. El ángulo diedro de una cúpula triangular entre un cuadrado y un triángulo es de aproximadamente 125°, el de un cuadrado y un hexágono es de 54,7° y el de un triángulo y un hexágono es de 70,5°. Por lo tanto, el ángulo diedro de un cuboctaedro entre un cuadrado y un triángulo, en el borde donde se unen las bases de dos cúpulas triangulares es de 54,7° + 70,5° aproximadamente 125°. Por lo tanto, el ángulo diedro de un cuboctaedro entre un cuadrado y un triángulo es de aproximadamente 125°. [7]

El proceso de transformación del jitterbug

Buckminster Fuller descubrió que el cuboctaedro es el único poliedro en el que la distancia entre su centro y el vértice es la misma que la distancia entre sus aristas. En otras palabras, tiene los mismos vectores de longitud en el espacio tridimensional, conocido como equilibrio vectorial . [8] Los puntales rígidos y los vértices flexibles de un cuboctaedro también pueden transformarse progresivamente en un icosaedro regular , un octaedro regular o un tetraedro regular. Fuller denominó a esto la transformación jitterbug . [9]

Un cuboctaedro tiene la propiedad de Rupert , lo que significa que hay un poliedro del mismo tamaño o mayor que puede pasar a través de su agujero. [10]

Simetría y clasificación

Modelo 3D de un cuboctaedro

El cuboctaedro es un sólido arquimediano , es decir, un poliedro altamente simétrico y semirregular, y dos o más caras poligonales regulares diferentes se encuentran en un vértice. [11] El cuboctaedro tiene dos simetrías, resultantes de las construcciones mencionadas anteriormente: la misma simetría que el octaedro o cubo regular, la simetría octaédrica , y la misma simetría que el tetraedro regular, la simetría tetraédrica . [12] Las caras poligonales que se encuentran en cada vértice son dos triángulos equiláteros y dos cuadrados, y la figura del vértice de un cuboctaedro es 3.4.3.4. El dual de un cuboctaedro es el dodecaedro rómbico . [13] Oh yo {\displaystyle \mathrm {O} _ {\mathrm {h} }} yo d {\displaystyle \mathrm {T} _ {\mathrm {d} }}

Simetría equilátera radial

En un cuboctaedro, el radio largo (centro a vértice) es el mismo que la longitud de la arista; por lo tanto, su diámetro largo (vértice a vértice opuesto) es 2 longitudes de arista. [14] Su centro es como el vértice apical de una pirámide canónica: a una longitud de arista de todos los demás vértices. (En el caso del cuboctaedro, el centro es de hecho el vértice de 6 pirámides cuadradas y 8 triangulares). Esta simetría equilátera radial es una propiedad de solo unos pocos politopos uniformes, incluido el hexágono bidimensional , el cuboctaedro tridimensional y el teseracto de 24 y 8 celdas de cuatro dimensiones . [15] Los politopos radialmente equiláteros son aquellos que se pueden construir, con sus radios largos, a partir de triángulos equiláteros que se encuentran en el centro del politopo, cada uno contribuyendo con dos radios y una arista. Por lo tanto, todos los elementos interiores que se encuentran en el centro de estos politopos tienen caras internas de triángulos equiláteros, como en la disección del cuboctaedro en 6 pirámides cuadradas y 8 tetraedros.

Cada uno de estos politopos radialmente equiláteros también se presenta como celdas de una teselación característica que llena el espacio : la teselación de hexágonos regulares, el panal cúbico rectificado (de cuboctaedros y octaedros alternados), el panal de 24 celdas y el panal teseractico , respectivamente. [16] Cada teselación tiene una teselación dual ; los centros de celda en una teselación son los vértices de celda en su teselación dual. El empaquetamiento de esferas regular más denso conocido en dos, tres y cuatro dimensiones utiliza los centros de celda de una de estas teselaciones como centros de esferas.

Como es radialmente equilátero, el centro del cuboctaedro está a una distancia de una arista de los 12 vértices.

El cuboctaedro, cubohemioctaedro y octahemioctaedro .

El cuboctaedro comparte su esqueleto con los dos poliedros uniformes no convexos , el cubohemioctaedro y el octahemioctaedro . Estos poliedros se construyen a partir del esqueleto de un cuboctaedro en el que los cuatro planos hexagonales bisecan su diagonal, intersectando su interior. Al sumar seis cuadrados u ocho triángulos equiláteros se obtiene el cubohemicotaedro o el octahemioctaedro, respectivamente. [17]

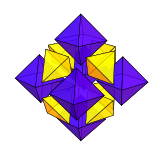
El cuboctaedro 2-cubre al tetrahemihexaedro , que por consiguiente tiene la misma figura abstracta de vértice (dos triángulos y dos cuadrados: ) y la mitad de los vértices, aristas y caras. (La figura real del vértice del tetrahemihexaedro es , con el factor debido a la cruz.) [18] 3 ⋅ 4 ⋅ 3 ⋅ 4 {\displaystyle 3\cdot 4\cdot 3\cdot 4} 3 ⋅ 4 ⋅ 3 2 ⋅ 4 {\textstyle 3\cdot 4\cdot {\frac {3}{2}}\cdot 4} a 2 {\textstyle {\frac {a}{2}}}

La disección en pirámides cuadradas y tetraedros

El cuboctaedro se puede dividir en 6 pirámides cuadradas y 8 tetraedros que se encuentran en un punto central. Esta división se expresa en el panal tetraédrico-octaédrico, donde pares de pirámides cuadradas se combinan para formar octaedros . [19]

Gráfico

La gráfica de un cuboctaedro

El esqueleto de un cuboctaedro puede representarse como el grafo , uno de los grafos de Arquímedes . Tiene 12 vértices y 24 aristas. Es un grafo cuártico , que tiene cuatro vértices que conectan cada vértice. [20]

El gráfico de un cuboctaedro puede construirse como el gráfico lineal del cubo, convirtiéndose en el gráfico localmente lineal . [21]

Apariencia

El cuboctaedro era probablemente conocido por Platón : en Definitiones de Heron se cita a Arquímedes diciendo que Platón conocía un sólido formado por 8 triángulos y 6 cuadrados. [22]

Referencias

Notas al pie

  1. ^ Coxeter 1973, págs. 18-19, §2.3 Poliedros cuasirregulares.
  2. ^
    • Berman 1971
    • Ogievetsky y Shlosman 2021, pág. 477
  3. ^ van Leeuwen, Freixa y Cano 2023, pag. 50.
  4. ^ Linti 2013, pág. 41.
  5. ^Por Berman 1971.
  6. ^ Coxeter 1973, p. 52, §3.7 Coordenadas de los vértices de los sólidos regulares y cuasi-regulares.
  7. ^ Johnson 1966.
  8. ^ Cockram 2020, pág. 53.
  9. ^ Verheyen 1989.
  10. ^ Chai, Yuan y Zamfirescu 2018.
  11. ^ Diudea 2018, pág. 39.
  12. ^
    • Koca y Koca (2013), pág. 48
    • Cromwell (1997). Para la simetría octaédrica, véase la pág. 378, Figura 10.13. Para la simetría tetraédrica, véase la pág. 380, Figura 10.15.
  13. ^ Williams 1979, pág. 74.
  14. ^ Coxeter 1973, p. 69, §4.7 Otros panales.
  15. ^ Coxeter 1973, págs. 292–293, Tabla I (ii): columna 0 R/l .
  16. ^ Coxeter 1973, p. 296, Tabla II: Panales regulares.
  17. ^
    • Pisanski y Servatius 2013, pág. 108
    • Barnes 2012, pág. 53
  18. ^ Grünbaum 2003, pág. 338.
  19. ^ Posamentier y col. 2022, pág. 233–235.
  20. ^ Read y Wilson 1998, pág. 269.
  21. ^ Fan 1996.
  22. ^ Turnball 1931.

Obras citadas

  • Barnes, J. (2012). Joyas de la geometría . Springer . doi :10.1007/978-3-642-30964-9. ISBN. 978-3-642-30964-9.
  • Berman, Martin (1971). "Poliedros convexos de caras regulares". Revista del Instituto Franklin . 291 (5): 329–352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
  • Chai, Ying; Yuan, Liping; Zamfirescu, Tudor (2018). "Propiedad de Rupert de los sólidos arquimedianos". The American Mathematical Monthly . 125 (6): 497–504. doi :10.1080/00029890.2018.1449505. S2CID  125508192.
  • Cockram, Bernice (2020). En foco Geometría sagrada: tu guía personal. Wellfleet Press. ISBN 978-1-57715-225-5.
  • Coxeter, HSM (1973) [1948]. Politopos regulares (3.ª ed.). Nueva York: Dover Publications .
  • Cromwell, Peter R. (1997), Poliedros, Cambridge University Press , ISBN 978-0-521-55432-9
  • Diudea, MV (2018). Cúmulos poliédricos de múltiples capas. Materiales de carbono: química y física. Vol. 10. Springer . doi :10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
  • Fan, Cong (1996). "Sobre jaulas generalizadas". Journal of Graph Theory . 23 (1): 21–31. doi :10.1002/(SICI)1097-0118(199609)23:1<21::AID-JGT2>3.0.CO;2-M. MR  1402135.
  • Ghyka, Matila (1977). La geometría del arte y la vida (ed. [Nachdr.]). Nueva York: Dover Publications . págs. 51–56, 81–84. ISBN 9780486235424.
  • "Grünbaum, Branko (2003). ""Nuevos" poliedros uniformes". En Bezdek, Andras (ed.). Geometría discreta . CRC Press . ISBN 9780203911211.
  • Johnson, Norman W. (1966). "Poliedros convexos con caras regulares". Revista Canadiense de Matemáticas . 18 : 169–200. doi : 10.4153/cjm-1966-021-8 . MR  0185507. S2CID  122006114. Zbl  0132.14603.
  • Koca, M.; Koca, NO (2013). "Grupos de Coxeter, cuaterniones, simetrías de poliedros y politopos 4D". Física matemática: Actas de la 13.ª Conferencia Regional, Antalya, Turquía, 27-31 de octubre de 2010. World Scientific.
  • Linti, G. (2013). "Compuestos encadenados - Grupo 13 [Al, Ga, In, Tl]". En Reedijk, J.; Poeppelmmeier, K. (eds.). Química inorgánica integral II: de los elementos a las aplicaciones . Newnes.
  • Ogievetsky, O.; Shlosman, S. (2021). "Compuestos y cilindros platónicos". En Novikov, S.; Krichever, I.; Ogievetsky, O.; Shlosman, S. (eds.). Integrabilidad, cuantificación y geometría: II. Teorías cuánticas y geometría algebraica. American Mathematical Society . ISBN 978-1-4704-5592-7.
  • Pisanski, T.; Servatius, B. (2013). Configuración desde un punto de vista gráfico. Springer. doi :10.1007/978-0-8176-8364-1. ISBN. 978-0-8176-8363-4.
  • Posamentier, AS; Thaller, B.; Dorner, C.; Geretschläger, R.; Maresch, G.; Spreitzer, C.; Stuhlpfarrer, D. (2022). Geometría en nuestro mundo tridimensional. Científico mundial . ISBN 978-981-12-3712-6.
  • Read, RC; Wilson, RJ (1998). Un atlas de gráficos . Oxford University Press .
  • Turnball, HW (1931). "Un manual de matemáticas griegas". Nature . 128 (3235): 739–740. Código Bibliográfico :1931Natur.128..739T. doi :10.1038/128739a0. S2CID  3994109.
  • van Leeuwen, P.; Freixa, Z.; Cano, I. (2023). "Una introducción a la quiralidad". Reacciones de formación de enlaces CC enantioselectivos: desde perspectivas de catálisis compleja, orgánica y biocatálisis de metales. Academic Press . ISBN 978-0-443-15774-5.
  • Verheyen, HF (1989). "El conjunto completo de transformadores Jitterbug y el análisis de su movimiento". Computers and Mathematics with Applications . 17 (1–3): 203–250. doi :10.1016/0898-1221(89)90160-0. MR  0994201.
  • Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño. Dover Publications, Inc. ISBN 978-0-486-23729-9.
  • Los poliedros uniformes
  • Poliedros de realidad virtual La enciclopedia de poliedros
  • Weisstein, Eric W. , "Cuboctaedro" ("Sólido arquimediano") en MathWorld .
  • El Cuboctaedro en Hexnet, un sitio web dedicado a las matemáticas hexagonales.
  • Klitzing, Richard. "Poliedros uniformes convexos 3D o3x4o - co".
  • Red editable e imprimible de un cuboctaedro con vista 3D interactiva
Obtenido de "https://es.wikipedia.org/w/index.php?title=Cuboctaedro&oldid=1250202808"